基于改进集合经验模态分解和深度信念网络的出水总磷预测

王龙洋，蒙西，乔俊飞

（1北京工业大学信息学部，北京100124；2计算智能与智能系统北京市重点实验室，北京100124）

引 言

城市污水处理过程是一个复杂的生化反应过程，具有随机性、强耦合性、高度非线性等一系列特征，其关键水质参数的有效预测是保证污水处理厂高效、稳定运行的先决条件。出水总磷是衡量城市污水处理过程出水水质的一种重要参数，当水体中总磷含量超过一定限度时，会导致水体营养物质富集，造成水生植物异常繁殖。因此，严格限制出水总磷排放浓度尤为重要[1]。研究表明，加强对出水总磷浓度的预测是有效预防并减轻水体富营养化问题的重要举措。然而，由于城市污水处理过程是一个复杂的动态过程，城市污水处理过程出水总磷的预测主要通过基于机理建模的软测量技术实现。而现有的机理模型无法很好地体现出污水处理过程的全部特性，预测的精度往往不够理想。因此，如何建立精准、可靠的城市污水处理过程出水总磷预测模型是污水处理过程领域亟待解决的问题。

受上述问题驱动，基于智能算法的预测方法在城市污水处理过程水质参数预测领域得到了广泛关注和应用[2]。人工神经网络(artificial neural network,ANN)作为一种非常成熟的智能算法，由于具备较理想的非线性逼近能力和抗干扰能力，被广泛应用于污水处理过程建模领域。例如，杨琴等[3]设计了一种基于BP神经网络的水质参数预测模型，该模型采用水温、pH等参数作为模型输入变量，对水质参数进行预测，取得了较好的预测结果。Hong等[4]提出了一种前馈神经网络预测方法，该方法将pH、氧化还原电位和溶解氧浓度的参数作为变量输入，并采用前馈神经网络建立模型进行预测，取得了比较理想的预测结果。另外，Bagheri等[5]设计了径向基函数网络水质参数预测模型，并将其用于水质预测，实验表明，该预测方法具有较理想的预测效果。Han等[6]用一种改进的粒子群算法对RBF神经网络结构和网络参数进行同步优化，构建了基于自组织RBF神经网络的水质预测模型。上述基于神经网络的预测方法虽然在一定程度上取得了比较理想的预测结果，但所采用的神经网络均是浅层结构，当网络学习对象变量较多时，浅层结构常常不能满足水质预测精度的要求[7]。

针对以上问题，专家学者研究了深度学习模型预测方法。王功明等[8]将深度信念网络和偏最小二乘回归算法相结合对水质参数进行预测，结果表明，该方法取得了比较满意的预测结果。Wang等[9]提出了基于信息相关的深度信念网络方法，并将其用于水质的预测，提高了水质预测精度。虽然以上方法在一定程度上解决了浅层网络水质预测所存在的不足，但是在水质参数预测过程中采用的辅助输入变量过多，变量间复杂的关系会相互影响，导致了模型预测精度的降低。为此，Zou等[10]设计了基于长短时间记忆神经网络的预测模型，并将其应用于水质参数预测。该方法虽然解决了水质参数预测过程中输入变量过多的问题，但是忽略了水质序列数据之间存在自相关性问题，致使神经网络没有学习到水质参数预测模型，而是学习到了自相关性，从而极大地降低了网络的预测精度。因此，建立一种理想的水质预测模型，消除水质数据自相关，提高预测精度迫在眉睫。

由于模型的预测性能极大地依赖于网络的结构，为了进一步提高模型的预测精度，Srivastava等[11]采用随机dropout算法来随机修剪DBN的神经元和它们之间的权值连接，从而获得一个精简结构的DBN。Shen等[12]通过采用连续dropout算法来提取DBN隐含层神经元独立信息特征，获得了较为理想的网络结构。然而在上述一系列方法中，由于存在冗余神经元，在一定程度上增加了计算复杂度。为了解决上述问题，一些进化算法被引进了神经网络。Hayashida等[13]提出了一个基于遗传算法的DBN结构优化方法，仿真结果表明，GA-DBN能获得合适的结构，具有较高的预测性能。然而遗传算法实现较为复杂，而且很难收敛到全局最优，因此遗传算法的广泛使用受到了限制。文献[14]中设计了一个GPSO-DFNN算法，在GPSO-DFNN中，利用基于高斯函数的混沌映射平衡粒子群算法中粒子的检测和利用能力。并在此基础上，进一步实现了DFNN结构优化，提高了模型计算效率。然而该研究仅针对的是浅层神经网络，而对于深度神经网络的研究还是个开放的课题。

因此，受上述研究所启发，本文提出了一种基于MEEMD-DBN-SA的城市污水处理过程出水总磷预测方法。

1 理论阐述

1.1 深度信念网络

DBN是一种应用非常广泛的深度学习模型，其由多个受限Boltzmann机(restricted Boltzmann machines,RBM)顺序堆叠而成。而RBM[15-17]作为DBN的核心组成部分，它由一个可视层和一个隐含层构成。通常前一个RBM的激活输出作为后一个堆叠RBM的输入数据，并采用快速贪婪搜索方法进行学习[18-19]，其模型结构图如图1所示。

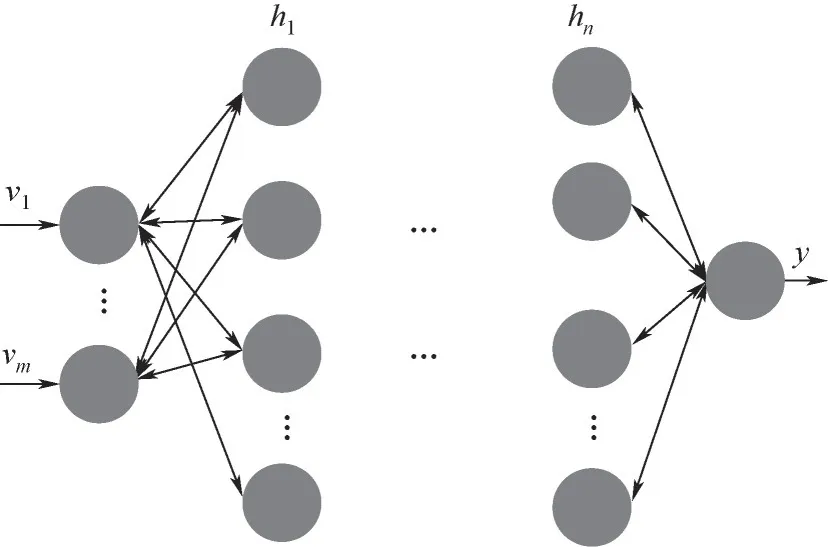
图1 深度信念网络模型结构图Fig.1 Structure diagramof deep belief network model

RBM是一种特殊的基于能量的统计模型。其能量函数表达式如式(1)所示：

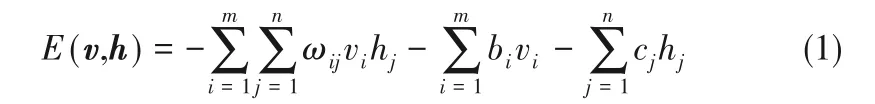
其中，ωij表示对称权值；v=(v1,v2,…,vm)表示可视层，h=(h1,h2,…,hn)表示隐含层。vi,hj分别表示可视单元和隐含单元的二值状态；bi，cj表示对应的可视层与隐含层偏置。

RBM通过能量函数来分配可视状态和隐含状态向量的联合概率，其表达式如式(2)所示：

其中，＜vihj＞data和＜vihj＞model分别表示数据分布与模型分布的期望。

采用对比散度算法来粗略逼近梯度[20]，表达式如式(6)所示：

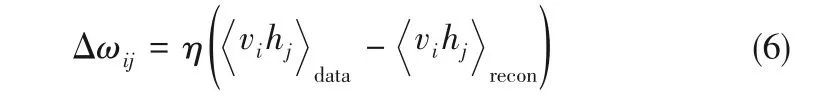
其中，＜vihj＞recon代表由输入数据初始化得到的重构状态的期望；η代表学习率。

1.2 MEEMD算法

MEEMD算法是在集合经验模态分解(ensemble empirical mode decomposition,EEMD)的基础上进行改进而得到的，改进后的MEEMD算法不仅能够解决经验模态分解(empirical mode decomposition,EMD)[21-22]存在的模态混淆问题，而且可以解决EEMD[23]、互补集合经验模态分解等算法所存在的计算量大、重构误差和伪分量问题。城市污水处理过程的出水总磷数据由于数据之间存在自相关性，因此可以采用MEEMD方法对其进行信号分解，来消除这种自相关性。MEEMD算法分解总磷数据的步骤如下。

（1）首先，基于互补集合经验模态分解算法对将要研究的总磷数据信号按照瞬时频率的高低依次进行分解。

（2）其次，对步骤(1)分解后得到的分量进行排列熵[24]值计算，借助于排列熵来检测分量是否存在异常，如果排列熵数值大于所设定的阈值，就认为该分量是异常分量，则可以将异常分量直接去除。反之则认为是近似平稳的分量，则可以保留下来。排列熵是一种时间序列的随机检测方法，熵值越大说明序列越随机，熵值越小说明序列越规则，且排列熵取值在[0,1]区间，便于控制。

（3）最后，对剩余的分量进行EMD分解，并对所得到的所有固有模态分量按照频率从高到低的顺序依次进行排列。

1.3 模拟退火算法

模拟退火算法是一种非线性反演方法[25-26]，模拟退火的实质是现代Monte Carlo法，该算法的求解过程是一个不断寻优的过程，在寻优过程中，拟合度随着迭代次数的增加而不断变化，呈现出高低起伏的态势，但总体是朝着变大或变小的方向。得益于模拟退火容许拟合度变小以及拟合误差变大，这样就利于模型从局部最优值中跳出，得到最终所期望的全局优化模型。

2 模型构建

2.1 建模策略

水体中总磷元素超标，会引起水生藻类植物大量繁殖，从而导致水体富营养化、生态失衡等严重后果。因此，加强对水体中总磷浓度的预测，并实现城市污水处理过程出水总磷的精准预测具有非常积极的意义。为了实现上述目标，文中设计了一种基于MEEMD-DBN-SA的城市污水处理过程出水总磷预测模型。基本建模思路是：首先，从北京市朝阳区某污水处理厂获得污水处理过程出水总磷实际数据，并进行数据的预处理，得到较为理想的样本数据集；其次，将历史时刻的出水总磷样本数据作为输入变量，进行下一时刻的出水总磷预测，来有效避免输入变量过多造成模型预测精度下降的问题；然后，基于MEEMD算法对出水总磷数据进行信号分解，获得若干个IMF分量，并计算每个IMF分量的排列熵；通过设置合适的阈值，将大于阈值的异常分量剔除，可以有效消除分解过程中所产生的伪IMF分量和数据之间的自相关性，从而进一步提高模型预测精度；最后，将剩余的IMF分量作为最终建模的输入，分别建立DBN预测模型；同时，为进一步提高模型预测精度，采用模拟退火算法对DBN进行结构优化，并将优化结构后获得的各个DBN预测值进行重构相加，得到最终的出水总磷预测结果。

2.2 基于MEEMD-DBN的出水总磷预测模型设计

污水处理过程中的出水总磷预测作为一种广义上的时间序列模型，本文采用历史时刻的污水处理过程出水总磷数据作为输入，并把第n+1时刻的数据作为输出，进行滚动建模，一般情况下，这样的建模预测结果都较为理想。但是总磷序列数据之间所存在的严重滞后和预测精度不高问题却不容忽视，主要原因是出水总磷时间序列存在自相关，事实上DBN并没有学习到出水总磷预测模型，而是学到了这种自相关性。因此，本文首先基于MEEMD算法对复杂的出水总磷序列信号进行分解，消除序列的自相关性，并剔除分解后存在的伪IMF分量；然后，对剩余的每个IMF分量分别建立DBN预测模型，为了进一步提高模型的总磷预测精度，采用模拟退火算法对DBN的结构模型进行优化，从而得到最优的IMF分量预测结果；最后将各IMF对应的DBN的预测值重构相加。其模型结构框图如图2所示。

采用MEEMD-DBN-SA模型进行出水总磷预测的详细步骤如下。

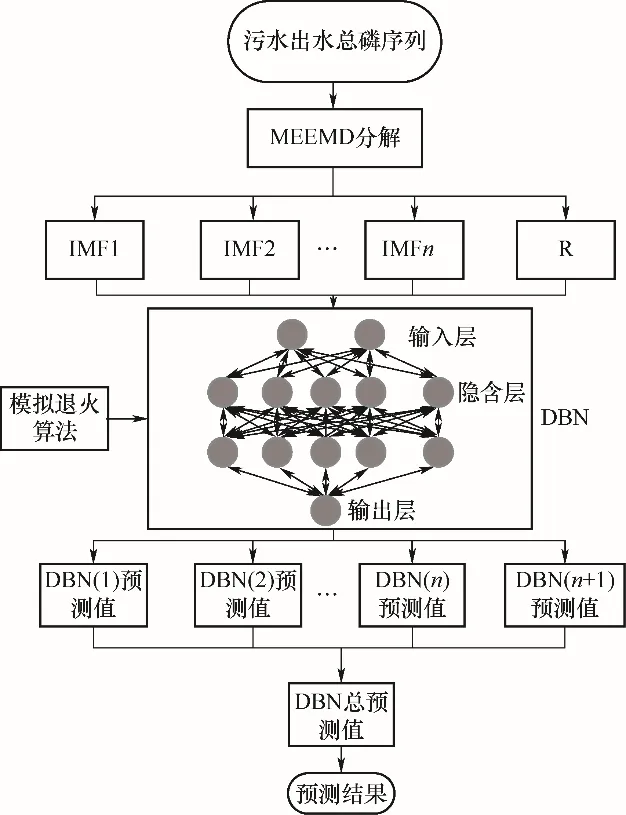
图2 MEEMD-DBN-SA模型结构框图Fig.2 Block diagram of MEEMD-DBN-SA model

（1）从北京某污水处理厂采集到污水处理过程出水总磷数据，然后经过数据预处理，得到样本数据。

（2）采用MEEMD算法对输入的总磷序列数据非平稳信号进行分解，分解过程如下。

①在原始信号H(t)中，分别添加均值为0的白噪声信号sj(t)和-sj(t)，其代数表达式如式(7)和式(8)所示：

③计算集成后分量ℓp(t)的排列熵，并设置阈值θ，如果分量的熵值大于θ，则被视为是异常分量，并剔除异常分量;小于θ值，则被视为近似平稳分量，保留下来。

④将已分解的前p个分量从原始信号中分离出来，即

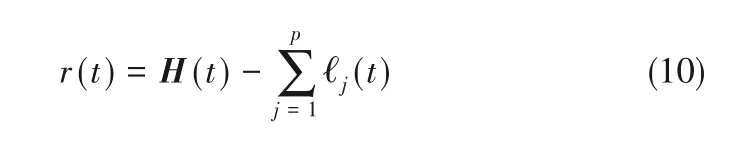
再对剩余信号r(t)进行EMD分解，将得到的所有IMF分量按高频到低频顺序排列。

（3）将步骤(2)分解后得到的各个IMF分量分别输入DBN中进行预测。其详细步骤如下。

①创建一个初始的DBN结构，并且用无监督学习初始化DBN所有的连接权重。

②将IMF输入分量输入DBN可视层v以后，采用对比散度算法进行训练，对于所有的隐含层单元j计算p(hj=1/v)用给定的计算式(4)。然后通过p(hj=1/v)采样得到h∈[0,1]，其计算表达式如式(11)所示：

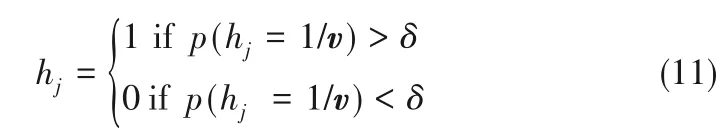
其中，δ是常数，其变化范围为0.5～1。

③对于所有的可视层单元i，计算p(vi=1/h)用采样h，其计算表达式如式(3)所示。然后通过p(vi=1/h)采样得到v^∈[0,1]，计算表达式如式(12)所示。

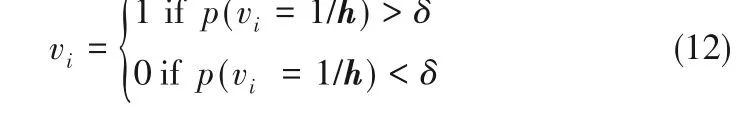
④然后对所有的隐含层单元j，计算p(hj=1/v)通过采样v，其计算表达式如式(4)所示，然后通过p(hj=1/v)采样得到h^∈[0,1]，其计算表达式如式(11)所示。

⑤采用Gibbs采样法确定模型中抽样数据的期望。

⑥用Gibbs采样法来计算训练集中观测数据的期望与模型中抽样数据的期望之间的误差，其计算表达式如式(5)所示。

⑦在有监督微调阶段利用BP算法对整个网络进行逐步微调即可。

（4）考虑到在预测过程中DBN的网络结构难以确定，于是采用模拟退火算法对DBN的结构进行优化。

（5）将最终优化结构后DBN的各IMF分量预测结果相加重构，从而得到最终的预测结果。

2.3 算法计算复杂度分析

水质数据输入MEEMD算法中进行经验模态分解，假如，经过l次分解得到l个分量，然后计算排列熵需要计算l2次，然后判断是否存在异常分量需要l次判断，则最终计算复杂度大致为O(l2)。对于深度信念网络，一般两个隐含层即可解决绝大部分的问题，假设输入层神经元个数为n1，第一个隐含层神经元个数为n2，第二个隐含层神经元个数为n3，第三个隐含层神经元个数为n4，设输入样本个数为m，则在前向传播过程中计算复杂度为O(m(n1n2+n2n3+n3n4))，由于n1和n4均为定值，都是常数，则前向传播的计算复杂度为O(m(n2+n2n3+n3))。同理，反向传播的计算复杂度也为O(m(n2+n2n3+n3))，则深度信念网络的计算复杂度为O(m(n2+n2n3+n3))。采用模拟退火算法优化结构过程中其目标函数的计算复杂度是O(s)，假定温度控制外循环次数为a，在每个特定温度下内循环次数为b，那么整个算法的计算复杂度就是O(abs)。则最终模型的计算复杂度为O(l2+m(n2+n2n3+n3)+abs)。

3 实验结果及分析

为了验证所提出的MEEMD-DBN-SA出水总磷预测模型的有效性，本文将所提出的MEEMDDBN-SA在CO2浓度以及出水总磷数据集上进行了实验。此外，为了消除其他不相关因素对实验结果的影响，所有仿真实验的编译软件和计算机运行环境设置如下：编译软件为matlab2017b版，计算机处理器是Core i77770，并且CPU频率是3.6 GHz。

3.1 评价指标

衡量预测误差的指标有很多种，一般情况下，对于不同的任务需要采用的衡量指标也各不相同，出水总磷预测本质上属于回归任务，预测值通常为连续值，而对于预测任务常用的误差衡量指标有平均绝对误差(mean absolute error,MAE)[27]、均方误差(mean square error,MSE)[28-29]、均方根误差(root mean square error,RMSE)[30-31]、平均百分比误差(absolute percentage error,APE)。文中采用RMSE和APE两个性能指标来评估所设计模型的性能。RMSE和APE的表达式如式(13)和式(14)所示：

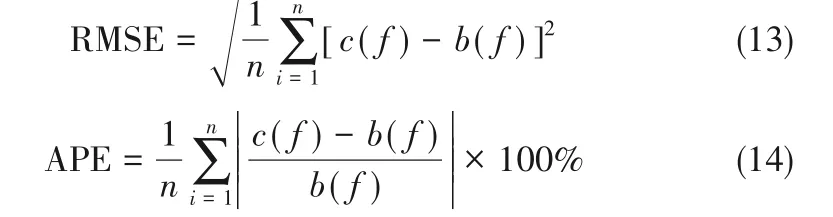
其中，n代表样本总数；c(f)代表真实值；b(f)代表预测值。

3.2 CO2浓度预测

环境问题一直以来都是世界上各国非常关注的问题之一，而CO2浓度的高低对环境的好坏起着至关重要的作用，如果大气中CO2浓度过高，会导致全球气候变暖，这一变化会产生灾难性的后果，而大气中CO2浓度过低就会导致植物的光合作用无法进行，从而使人们赖以生存的农作物无法存活。因此对某一地区CO2浓度变化进行预测，除了具有较好的科学研究意义，也能够在一定程度上为制定地区和企业CO2排放提供指导，具有一定的社会研究价值。由于受大气中众多不确定因素综合影响，CO2浓度变化序列数据具有随机性、高度非线性、非平稳性等特征。由于深度信念网络具有非线性逼近能力和抗噪声干扰能力，非常适用于非线性系统建模，同时由于CO2浓度序列数据存在着较强的自相关性，会显著影响模型的预测精度。采用MEEMD算法可以很好地去除CO2浓度序列数据的自相关性，提高模型预测精度。因此MEEMDDBN-SA模型对其有很好的适用性。采用夏威夷岛1965—1980年的总共192组数据进行实验，随机选取前100组数据作为训练样本进行训练，剩下的92组作为测试数据对网络进行测试。本实验结构参数设置如下：RBM训练次数为100次，网络最大迭代次数为1000次，学习率为0.1。实验采用历史时刻t-1时刻、t时刻的CO2数据来预测t+1时刻的CO2浓度，仿真结果如图3和图4所示。

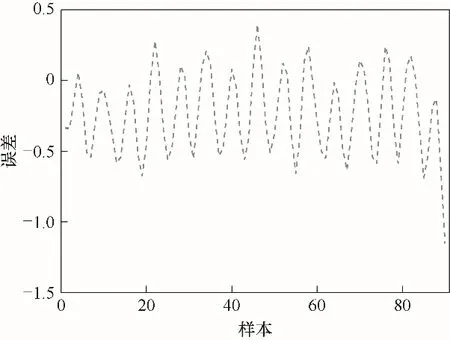
图3 CO2浓度预测误差Fig.3 Prediction error of CO2 concentration

图3为CO2浓度的预测误差曲线图，图像的横轴代表测试样本个数，纵轴代表的预测误差随着样本个数的变化而变化，从图中可以看出，误差曲线随着迭代次数的不断增加，一直在零值附近上下起伏，说明有较小的预测误差，所设计的模型有很好的拟合效果。图4为测试样本预测结果曲线，图像的横轴代表测试样本个数，纵轴代表出水CO2浓度，从图中可以看出，CO2浓度的预测值曲线紧紧跟随CO2浓度的实际值曲线，并随着测试样本的增加而变化，具有优良的跟踪性能和拟合效果。

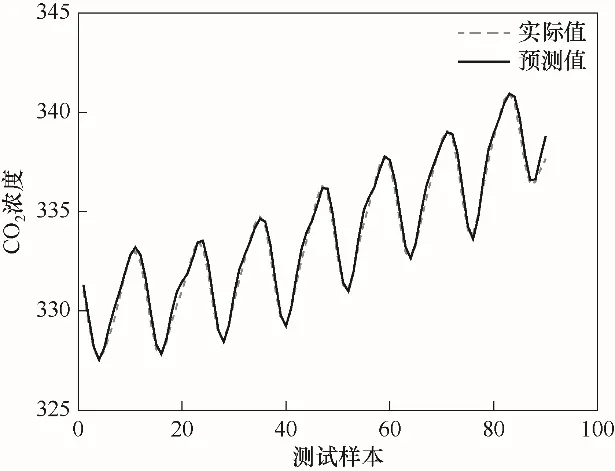
图4 测试样本预测结果曲线Fig.4 Prediction result curve of test sample

为了比较不同算法的预测性能，将本文所设计的MEEMD-DBN-SA算法与当前最新算法进行了比较，比较结果如表1所示。从表1可以看出，其他算法如BP神经网络算法在不同的文献中预测精度有较大差异，总地来说RMSE值处于1.3000～6.6000之间，而ALRDBN和CDBN的RMSE分别为1.1671和1.1507，相比BP算法均有一定程度的下降。采用DBN算法后，相比ALRDBN和CDBN却有所上升，经过MEEMD算法分解后的MEEMD-DBN的RMSE值和APE值下降较为明显，说明MEEMD分解取得了较好的作用。优化结构后的MEEMD-DBN-SA的RMSE值和APE值下降到0.3725和0.0008，在所有结果中RMSE值和APE值不仅是最小的，而且和其他算法明显拉开了差距，说明本文所设计的MEEMD-DBN-SA具有优异的预测性能。

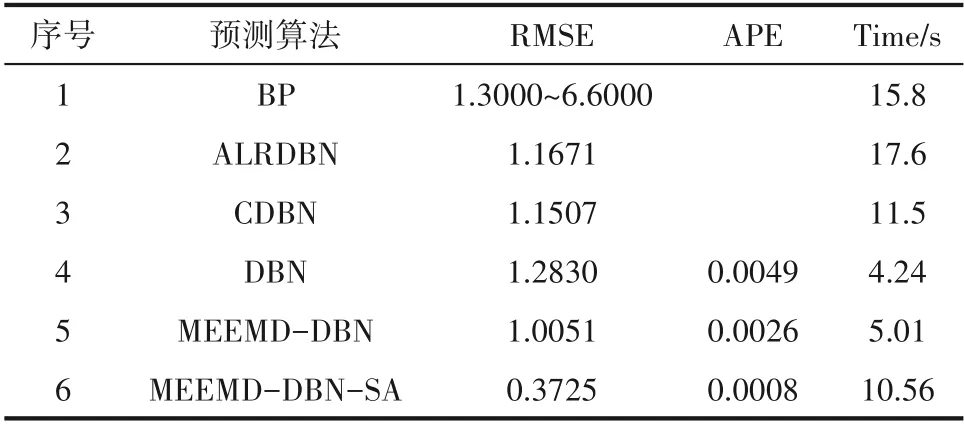
表1 不同算法性能比较Table 1 Performance comparison of different algorithms

本文算法的主要目的是提高模型的预测精度，但是为了了解算法的计算复杂度，并且考虑到一般情况下算法运行时间越长，计算复杂度越高，在表1中增加了算法的运行时间对比。从表1中可以看出，本文所设计的MEEMD-DBN-SA在所有算法中预测精度最高，运行时间为10.56 s，计算复杂度略有提升，但计算复杂度仍低于大部分算法。由于预测精度和计算复杂度在一定程度上是相互矛盾的，在保证预测精度的情况下，必然会增加计算复杂度。作为算法的折中，本文的MEEMD-DBN-SA算法仍具有良好的预测性能。

3.3 总磷预测

总磷是水体质量的一个很重要的评估标准，水体中若总磷含量过高，就会引起水体富营养化，藻类植物异常繁殖，因此预测水体中总磷含量至关重要，而总磷测量仪器测量总磷浓度不仅费时费力，而且难以进行有效测量，因此可以建立预测模型，通过历史时刻的数据来预测未来时刻的总磷含量，本研究建立了MEEMD-DBN-SA模型来实时预测水体中的总磷含量。从北京某污水处理厂采集到492组总磷数据，用400组数据作为训练数据，92组数据作为测试数据，本实验参数设置如下：RBM训练次数为100次，网络最大迭代次数为10000次，学习率为0.04。由历史时刻t-1时刻、t时刻的总磷数据来预测t+1时刻的总磷含量。其仿真结果如图5、图6所示。

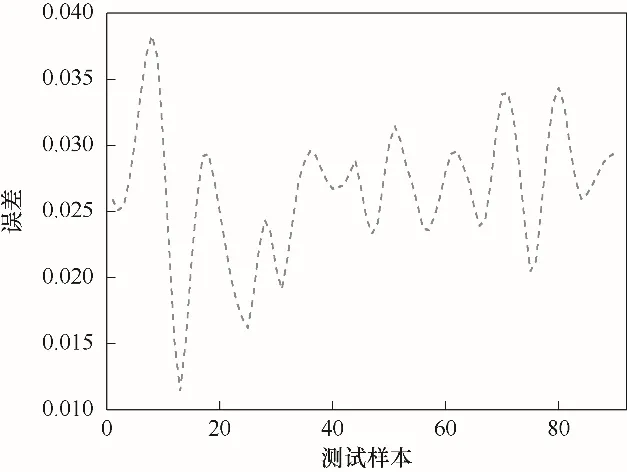
图5 出水总磷浓度预测误差Fig.5 Prediction error of total phosphorus concentration in effluent

图5为出水总磷浓度预测误差曲线图，图像的横轴代表测试样本的个数，纵轴代表的预测误差随着样本个数的变化而变化，从图中可以看出，误差曲线刚开始波动较剧烈，随着迭代次数的不断增加，误差越来越小，并逐渐向零值附近靠近，说明预测误差越来越小，所设计模型有很好的拟合效果。图6为测试样本预测结果曲线，图像的横轴代表测试样本的个数，纵轴代表出水总磷的浓度，从图中可以看出，出水总磷的预测值曲线紧紧跟随出水总磷的实际值曲线，并随着测试样本的增加而变化，具有优良的跟踪性能和拟合效果。

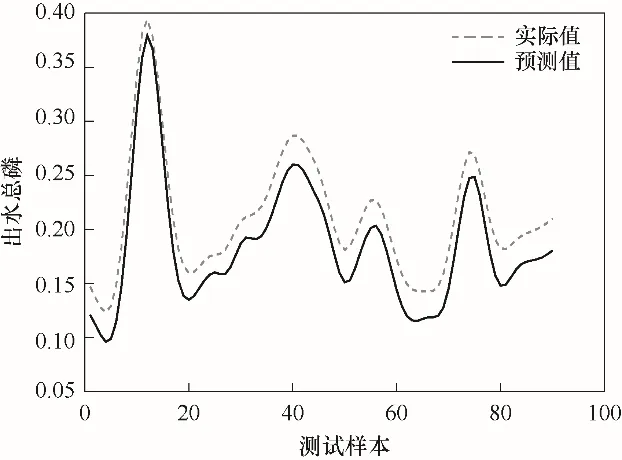
图6 测试样本预测结果曲线Fig.6 Prediction result curve of test sample

为了比较所设计的MEEMD-DBN-SA算法的有效性，将所设计的MEEMD-DBN-SA算法与其他算法进行了比较，比较结果如表2所示，从表中可以看出ILM-SVDFNN算法的RMSE值和APE值为0.1061和0.1161，LM-SVDFNN算法的RMSE值和APE值为0.1078和0.1167，ILM-FNN算法的RMSE值和APE值为0.1296和0.1412。而相比前几种算法，算法EBP-SVDFNN、EBP-FNN、GDFNN、MPCANN的RMSE值均在0.15以上，APE值也明显超过前述三种算法，甚至MPCA-NN的RMSE值超过了0.2，在所有算法中RMSE值最大，RBF、IELM和APSORBF算法的RMSE值和APE值与表中前8种算法相比都出现了小幅下降。而采用DBN算法后，RMSE值和APE值与部分算法相比优势不大。当采用MEEMD算法分解后，MEEMD-DBN的RMSE值得到了大幅度的下降，说明MEEMD分解起到了很好的效果，为进一步提高预测精度，采用模拟退火算法优化结构后，MEEMD-DBN-SA算法的RMSE值为0.0269，算法的RMSE值在所有算法中是最小的，且明显低于其他算法，APE值也几乎优于表中所有算法，从而很好地反映了MEEMD-DBN-SA算法的有效性。

本文算法的主要目的是提高出水总磷浓度的预测精度，从而避免水质超标排放，但为了明确算法的计算复杂度，在表2中增加了算法的运行时间对比，一般情况下，运行时间越长，则算法复杂度越高。由于预测精度和运行时间是两个相互矛盾的指标，当模型在迭代过程中，为获得更高的预测精度，就需要不断迭代，从而会造成运行时间延长，计算复杂度增加。相反，为了节省时间，减少迭代次数，虽然运行时间减少，算法计算复杂度降低，但预测精度则会大大降低。从表2中可以看出，本文设计的MEEMD-DBN-SA相比其他所有算法，预测精度得到非常显著的提升，由于引入了优化算法来优化模型的结构，计算时间为68.11 s，计算复杂度上升。相比其他算法，兼顾预测精度和计算复杂度，本文算法复杂度处于中等水平，但是预测精度却是所有方法中最高的，说明了所设计算法的有效性。

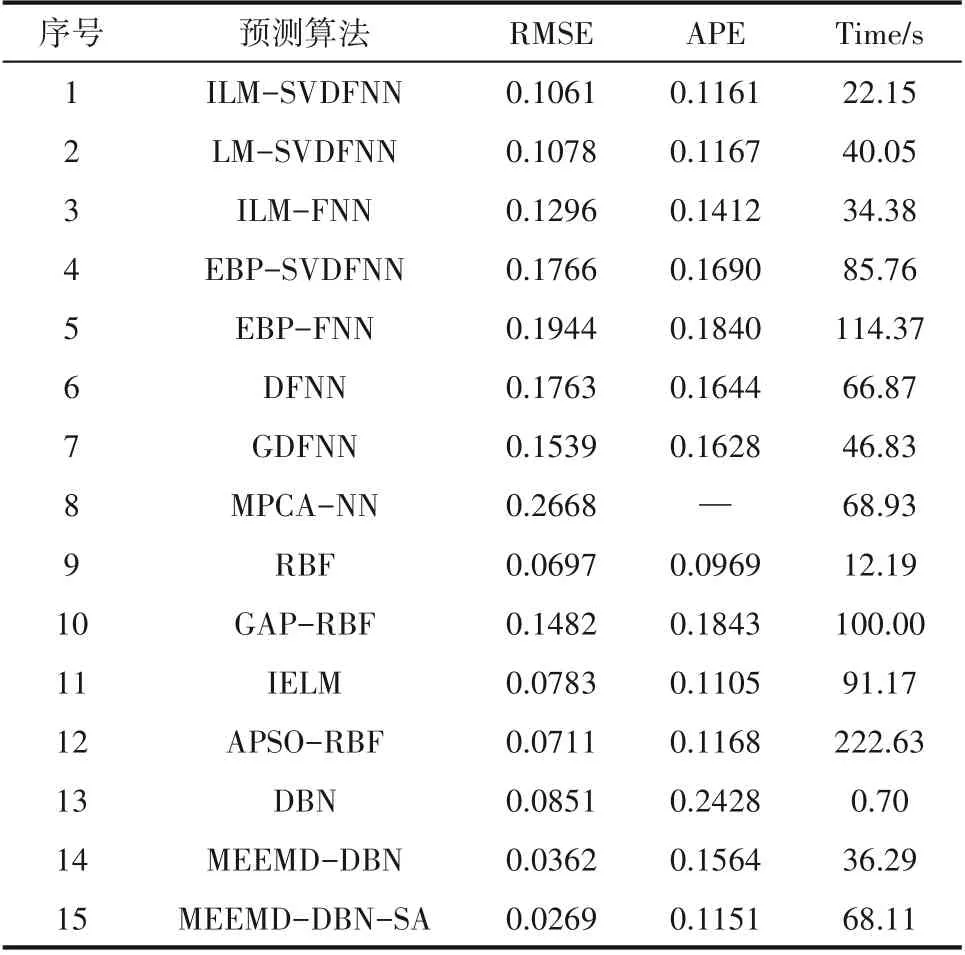
表2 不同算法性能比较Table 2 Performance comparison of different algorithms

4结 论

文中针对污水处理过程中出水总磷难以预测的问题，提出了一种基于改进的集合经验模态分解和深度信念网络的出水总磷预测方法。首先，文中将t-1、t时刻的总磷数据作为网络输入，来预测t+1时刻的出水总磷浓度，不仅有效地避免了辅助输入变量过多造成的模型预测精度下降问题，而且对t+1时刻出水总磷进行预测，可以提前了解水质状况并对水体合理加药，从而实现对超标水质的超前干预。其次，考虑到DBN在进行污水处理过程出水总磷数据预测时，由于出水总磷数据序列之间存在的自相关性，致使DBN不能学习到出水总磷之间真正的关系，而是学习到了数据之间的自相关性，于是基于MEEMD算法对出水总磷数据进行分解，获得若干个IMF分量，并计算每个IMF分量的排列熵。通过设置合适的阈值，将大于阈值的异常分量剔除，有效消除了分解过程中所产生的伪IMF分量和数据之间存在的自相关性，从而进一步提高模型预测精度。然后，将剩余的IMF分量作为最终建模的输入，分别建立深度信念网络预测模型。同时，采用模拟退火算法对DBN进行结构优化，以进一步解决预测模型中的网络结构问题，将优化结构后获得的各个DBN预测值进行重构相加，得到最终的预测结果。最后，模型构建完以后为验证MEEMDDBN-SA模型的有效性，将所设计的模型在CO2浓度以及现实污水处理过程出水总磷数据上进行了测试，仿真结果显示了MEEMD-DBN-SA模型的有效性。