池沸腾孤立气泡生长过程中微液层蒸发影响的实验和模拟耦合分析

潘丰，王超杰，母立众，贺缨

（大连理工大学能源与动力学院，辽宁大连116024）

引 言

沸腾传热是复杂的相变传热过程，几十年来，针对核态沸腾中的高效换热机制，学者们提出了诸多机理模型，包括瞬态导热、微对流和液层蒸发机理等。其中，瞬态导热理论认为热量的传递主要发生在气泡脱离阶段，气泡的脱离周期性地排开加热表面上的过热液体使得冷液体占据加热表面并与之发生热交换[1]。微对流理论认为沸腾换热的本质为被强化了的强制对流换热过程，其高效的换热性能来源于由气泡的周期性脱离而带来的强化效应，而并非相变过程本身[2]。而液层蒸发机理则认为，在气泡生长初期，不断生长的气泡将周围液体推开，在此过程中少量液体留在加热壁面上形成很薄的一层微液层[3]。同时，在气泡外侧的热边界层内则形成一层大液层[4]。气泡生长所需要的能量主要来源于加热表面上气泡底部及附近的过热液体层的相变潜热[5-6]。Tange等[7]利用背光法和PIV测速技术测量了沸腾过程中近壁面的流场，据此对瞬态导热、微对流和液层蒸发三种换热机理的传热系数进行了评估。他们认为随着沸腾热流的增大，液层蒸发占沸腾换热的比例持续增大，而微对流所占的比例逐渐减小。在高热通量区域(0.65 MW/m2)，液层蒸发所占的比例达到90%以上。

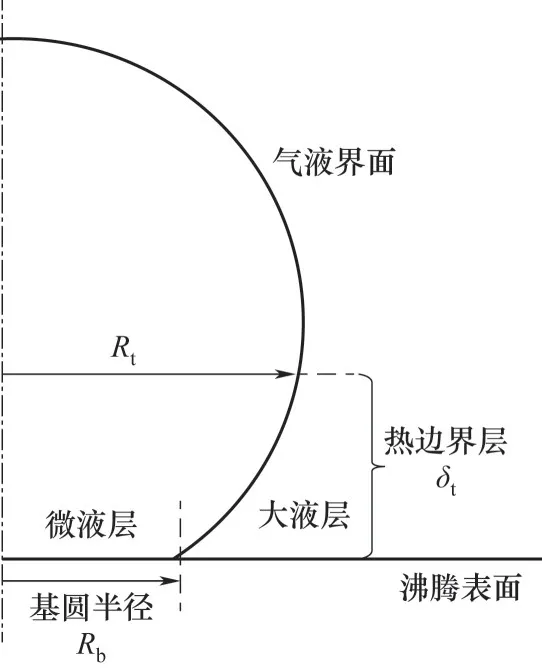
图1 气泡底部微液层与大液层区域示意图Fig.1 Schematic diagramof the microlayer and macrolayer underneath a vapor bubble

根据液层厚度的不同，气泡生长过程中底部液体层可分为三个区域，由内向外依次为：吸附层，微液层，大液层。其中吸附层为纳米量级，其换热通常忽略不计。如图1所示，气泡中心到气泡底部气液界面与加热表面接触点的距离定义为基圆半径。存在于气泡基圆半径内侧的为微液层，尺度较小，为微米量级。而大液层则为基圆半径以外到热边界层δt与气液界面交界位置Rt的液体层，其厚度为几百微米到毫米量级[8]。Sakashita等[9]测量了近临界热通量(CHF)处加热表面附近的空泡率，实验结果与大液层蒸发理论有较好的一致性：在高热通量区域，大液层蒸发消耗的热量占沸腾过程总传热量的94%。相比于大液层区域，尽管气泡底部的微液层区域较小，但由于该液体层在厚度方向上热阻较小，平均热通量高达1 MW/m2，在低热通量沸腾区域内，其换热量不容忽视[6]。Höhmann等[10]使用热色液晶(TLC)对沸腾过程中加热表面温度进行测量，结果表明气泡生长过程中大液层区域的温度基本稳定，而在宽度约50μm的微液层区域出现了明显的温降。类似地，Stephan等[11]通过红外相机观测了FC-84和FC-3284沸腾过程中不锈钢表面上的瞬态温度分布，同样发现加热表面上的低温区域出现在三相接触线附近的微小区域内；进一步的计算表明这一部分的换热量达到了总换热量的40%～60%。Nakabeppu等[6]则认为，气泡生长所需的能量约50%来源于微液层，其余则来自于气泡周围的大液层，且这一比例在不同的过热度下基本保持不变。陈宏霞等[12]对光滑单晶硅表面上不同热通量下单气泡沸腾过程中的壁面温度演变规律进行了对比分析，结果发现在高热流沸腾过程中，气泡底部形成了较大的干斑区域，导致汽化核心中心位置温度持续较高，而低温区域出现在大液层附近，因此此时相变换热主要发生在气泡两侧的大液层区域；而在低热通量区间内，气泡底部存在一层均匀的微液层，加热表面上对应地呈现出较大的低温区域，同时壁面温度分布表现为“中间低，两头高”。同时，他们在低热通量下的沸腾模拟结果也表明微液层的蒸发在气泡生长初期的贡献量高达90%以上[13]。而随着气泡的生长，微液层所占比重逐渐减小，在气泡脱离前微液层的蒸发占总换热量的52%。因此，观测加热壁面上气泡底层的液层动态分布有助于揭示沸腾传热机理，提出沸腾强化换热新手段[14]。

由于吸附层和微液层尺度较小，常规的观测手段只能观测到大液层区域，而沸腾过程中的微液层区域则处于气泡宏观基圆半径内侧的微观区域。近年来，借助先进的实验观测手段和逐渐完善的数值模型，沸腾过程中气泡底部的液层厚度变化及蒸发过程可以被较好地捕捉到。Nakabeppu等[6]借助微电子芯片(MEMS)传感器记录了气泡底层的温度场的动态变化，由此获得了气泡底部微液层区域的演变以及干斑区域的扩张和再润湿过程。他们测得基圆半径内侧瞬态热通量峰值高达2.8 MW/m2，并由此得到微液层厚度约为3μm。相比之下，基圆半径外侧热通量则不到0.4 MW/m2。Gong等[15]在ITO透明加热材料上进行了沸腾实验，使用非接触式的共焦光学探针，测量得到微液层的厚度为5～50 μm，大液层的厚度约为50～500μm。Zou等[8]应用飞秒级光源技术，产生了能在过冷沸腾过程中保持若干小时的单个蒸气泡，并对不同润湿性加热表面上的气泡底层的微液层进行了测量。结果表明，亲水表面上的气泡底层干斑区域较大且液层较薄，而疏水表面上微液层区域较大且液层较厚。利用激光消光法[16]和激光干涉法[17-19]对乙醇/去离子水沸腾实验时气泡底部液层结构的动态测量表明，微液层厚度均在1～5μm左右。同时，基圆半径在气泡生长初期不断外扩，气泡底层的微液层随之迅速增加。随着气泡的生长，微液层由于不断蒸发而逐渐变薄，并在中心区域出现干斑。而后，在气泡生长末期，干斑区域随着气泡基圆半径的收缩而重新润湿，最终气泡脱离时干斑区域与微液层区域均变为0。这些详实的观测结果为深入了解沸腾换热机理，精确分析沸腾传热过程奠定了理论基础。

目前，代表性的微液层蒸发模型[20-22]基本基于实验观测和气泡动力学分析。其中应用最为广泛的是Stephan等[23]基于雷诺润滑理论提出的静态微液层蒸发模型。该模型通过求解一个四阶非线性常微分方程来计算微液层厚度与相变热流。在此基础上，Jiang等[24]考虑了微液层的横向流动并结合接触线的移动和接触角的变化提出了动态微液层蒸发模型。相比之下，Sato等[25]提出的静态液层蒸发模型因具有参数少且简便有效等优点而在近年来被经常使用[13,26]。其模型基于Utaka等[16]的线性初始液层厚度假设提出：

该模型中唯一需要确定的参数为液层的初始斜率Cslope，对于去离子水在石英板上的沸腾过程，Utaka等[16]测得的取值为4.46×10-3，陈宏霞等[13]和王烨等[26]在模拟中也采用了这一数值。Sato等[25]在模拟铜表面上的沸腾过程时通过多次迭代匹配的方法，最终确定的数值为2.45×10-2。事实上，该参数在物理本质上表征着微液层前端微观接触角[18]的大小，因而与工质物性和加热表面的润湿性相关。对于不同的工质和加热面材料，该斜率的取值需要更多数据予以确认。

由于气泡底层结构复杂，且伴随着液层的蒸发和移动，尤其在不锈钢、铜等传统非透明金属表面上，微液层的厚度更加难以测量。而相比之下，气泡的一些宏观参数如基圆半径和气泡生长速率等则较容易获得。因此，本研究希望通过实验中测得的宏观气泡动态参数来确定微液层与大液层的蒸发在沸腾传热过程中的影响。在此基础上，通过建立沸腾界面传热模型来预测低热通量条件下铜表面上沸腾过程中气泡底部的微液层厚度，从而为进一步实现完整的沸腾过程模拟提供理论支持。

1 实验装置与数据处理

1.1 实验装置

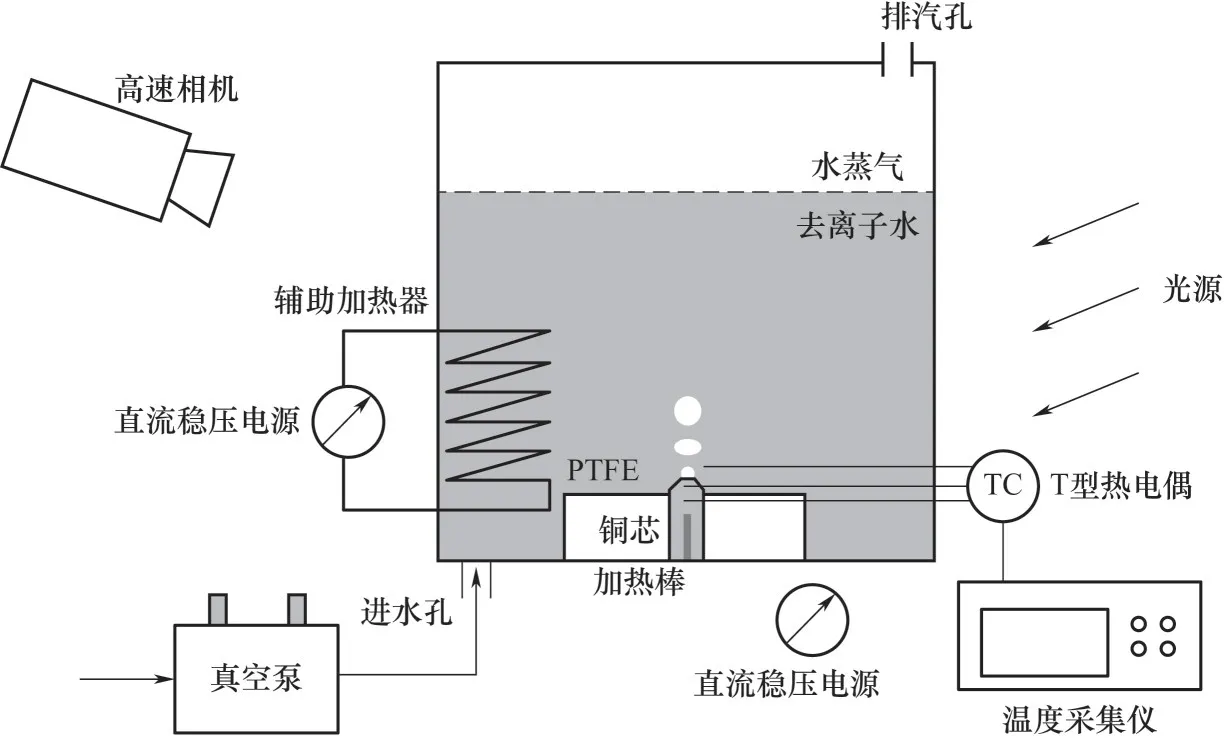
图2 单气泡池沸腾实验装置Fig.2 Schematic diagram of the experimental apparatus for single bubble boiling system

池沸腾实验装置示意图如图2所示。其中沸腾池为有机玻璃制成的透明容器，其尺寸为160 mm×160 mm×210 mm。容器顶部预留有排汽孔，容器内气压与环境保持相同。采用去离子水作为沸腾工质，实验前首先通过真空泵去除溶解在去离子水中的不凝气。主加热器置于容器底部，材质为铜，其上表面为加热表面，与去离子水直接接触，直径为10 mm。铜芯周围由聚四氟乙烯(PTFE)包裹以减少热量损失。铜芯底部固定有电阻加热棒，通过控制电阻棒两端电压可以实现不同的加热功率。铜芯内部不同深度(2.5 mm和7.5 mm)处固定有T形热电偶，据此可以对加热表面温度和热通量进行预估[27]。为了降低加热表面粗糙度以减少沸腾过程中气泡间的干涉，实验前首先采用不同型号砂纸(p180～p3000)对加热表面进行逐级打磨，随后在光滑加热表面中心加工单一孔穴以便产生单一汽化核心。当加热器温度逐渐升高时，加热面中心位置处的汽化核心会率先活化产生气泡。

实验过程中首先通过辅助加热器将去离子水加热至接近饱和状态。随后打开主加热器，通过电阻棒对铜芯进行加热。实时监测加热棒内温度分布，直至2 min内加热棒内温度变化不超过0.1℃认为达到稳态。逐级、缓慢调整加热功率至加热表面上汽化核心处有气泡产生，通过温度采集仪和高速相机分别记录加热表面温度变化和气泡生长图像。继续调整主加热器两端电压即可得到不同热通量下沸腾过程中加热表面的气泡生长过程。在整个过程中，通过热电偶实时监测沸腾池内主流体的温度，调节辅助加热器功率，使池内去离子水维持在饱和状态。

本实验系统中所用高速相机型号为Photron Fastcam Mini UX50,其在最大分辨率1280×1024下最大拍照速度为2000 fps，降低分辨率后其速度最高可达160000 fps，曝光时间为1.01～3.9μs。所匹配的显微镜头为体视显微镜，型号为Nikon SMZ800N，其放大倍数为5～480倍。T型热电偶温度采用Agilent 34970A结合34901A数据采集模块进行读取，响应速度10-5s,采用单通道测温时其最大扫描频率为60次/秒，多通道测温时扫描频率会随之降低。

1.2 气泡生长图像序列处理

为获取加热表面上气泡动态参数的变化，需首先对由高速相机获得的图片序列进行预处理以准确提取气泡边缘。如图3(a)所示，通过去除背景和高斯滤波后得到背景较为光滑连续的图像；然后调整对比度增强背景与气泡间的差异后进行图像二值化处理即可得到较为清晰的气泡形态；进一步将由光照引起的高亮部分进行填充，再进行边缘检测即可得到完整的气泡轮廓。图3(b)给出了气泡轮廓与原图像的比对结果，可以发现，本方法较好地还原了孤立气泡在加热表面上的生长过程。

1.3 误差分析

本实验中气泡体积计算的主要误差来源于气泡形状提取时的图像处理。气泡生长图像中610个像素点代表了真实加热表面上10 mm的区域，因此每个像素点对应的长度应为0.016 mm/pix，在气泡边界提取过程中引入的误差不超过3个像素点[28]即0.048 mm。气泡在脱离时的直径约为1.9 mm，高度为2.2 mm。气泡的体积采用微元法根据二维气泡形状计算得到，如图4所示，将气泡分割成N个微圆柱体(N=Hb/Δh)，其中Δh取一个像素的高度，将所有微圆柱体体积Vi叠加得到整个气泡的体积，即：

图3 气泡轮廓提取流程以及所提取到的气泡轮廓与原始图像的对比Fig.3 Theextracting procedure of bubble outlines and the comparison of the obtained bubble outlines with the original images

图4 基于微元法的气泡体积计算示意图Fig.4 The measurement of the bubble volume from the bubble growing images

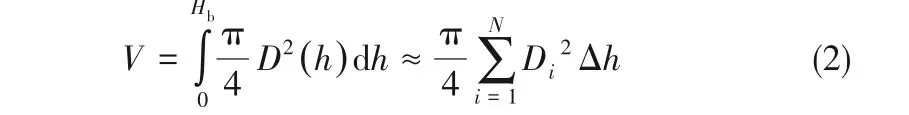
根据多参数单次间接测量误差传递公式[29]，间接测量得到的气泡体积的相对误差约为：

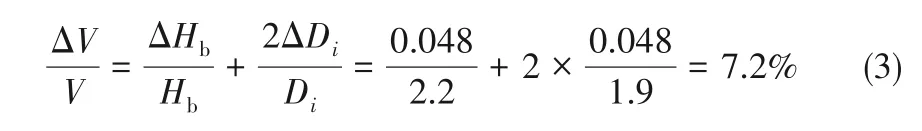
气泡基圆半径由气泡图像序列获得，平均值为0.2 mm，因此，其测量相对误差为ΔRb/Rb=0.048/0.2=24%。提取基圆半径时，由于采用同一分割阈值对一个气泡周期内的全部时序列图像进行处理，这一测量误差不会影响其在一个周期内的位置变化趋势。

加热器内的温度测量采用T型热电偶，测温不确定度为0.1 K。铜芯内的总热通量可根据其两端电压、电流和直径得到，其相对误差为[27]：

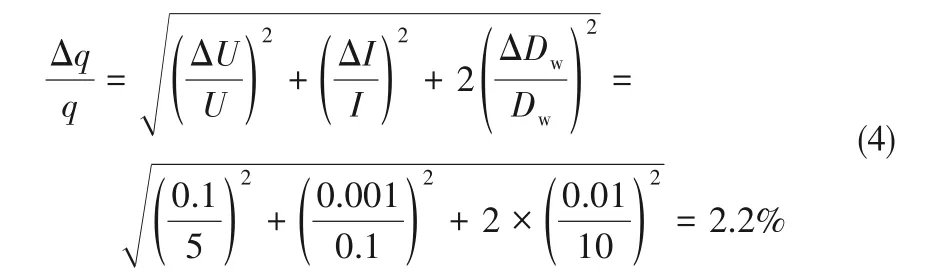
在后续模拟中，固体加热器底部采用实验中测得的温度作为定温边界条件，热通量的相对误差对沸腾实验有影响，但不影响后续的模拟分析。

2 实验结果与模拟分析

2.1 典型气泡生长周期内的气泡动态参数的变化

实验中首先对加热表面上的孤立气泡生长过程进行了观测。利用高速相机从沸腾池侧面对气泡的动态行为记录，拍照频率为3200 fps，图像分辨率为1/62 mm/pix。打孔前光滑加热表面粗糙度Ra约为0.15μm。采用去离子水作为沸腾工质。

图5所示为一个典型周期内气泡生长过程中的气液界面位置。加热表面过热度约为4.82 K，热通量5.5 kW/m2。在此工况下，气泡脱离直径为1.89 mm，气泡周期为46 ms，无等待周期。可以看出在整个气泡生长过程中，基圆半径的变化非常显著。由于气泡底部基圆半径的变化对加热表面换热特性有着重要的影响[6]，研究中根据气泡底部基圆半径的变化，将气泡的生长过程分为基圆半径迅速扩张-维持-迅速收缩三个阶段。图6(a)给出了气泡生长过程中高度和直径的变化。可以看到，在气泡生长前8 ms内，由于气泡底部基圆半径迅速向外扩张，气泡在横向和纵向均迅速增大且尺寸相当，形状更接近半圆形，这段时间约占气泡总周期的20%。在基圆半径相持阶段(8～40 ms)，气泡底部与加热表面接触线基本变化不大，气泡在纵向和横向的生长速度均有所减缓[图5(b)]；20 ms以后，气泡在纵向的尺寸略大于横向，纵向拉伸逐渐明显。当气泡临近脱离时，基圆半径在极短的时间内(3 ms)迅速缩减为0，气泡呈现明显的倒立水滴状，气泡半径基本不变，而纵向尺寸拉伸到最大，直至脱离加热表面[图5(c)]。

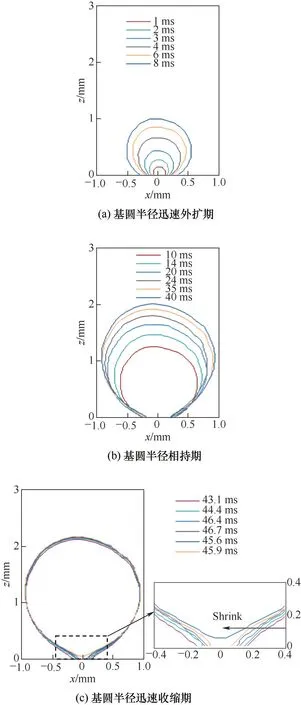
图5 气泡生长过程中不同阶段的气泡形状及底部基圆半径的变化Fig.5 The variation of vapor-liquid interface and bubble root during the bubble growing period

在此过程中，随着气泡受力情况的不断变化气泡的形状不断改变，其中气泡的脱离过程主要由气泡受到的浮力Fb和由表面张力引起的壁面附着力Fσ决定[24]：

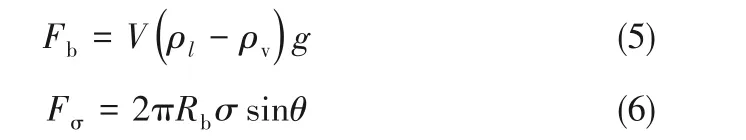
由式(6)可看出，壁面能提供的最大附着力主要由气泡底部基圆半径Rb和接触角θ的变化决定。图6(b)、(c)分别给出了气泡体积和气泡底部与加热表面接触角的变化。在气泡生长初期8 ms内接触角变化较快，由120°左右迅速减小至40°左右，随后保持在35°左右小范围波动，直到气泡临近脱离时减小到约30°。而气泡体积在气泡生长初期增长较快，8 ms时速率达到最大，这意味着气泡生长初期气液相变较多，而此时气液宏观接触面积较小[图5(a)]，因此相变主要发生在实验较难观测到的微液层区域。随后气泡体积增速逐渐减缓直至脱离时气泡体积达到最大，约3.7 mm3。根据式(5)和式(6)计算得到的气泡受到的浮力和壁面能提供的最大附着力如图6(d)所示。可以看到，在43 ms之前，气泡受到的浮力始终小于壁面能提供的最大附着力，因此气泡附着在壁面生长。43 ms时，气泡受到的浮力与壁面附着力持平。随后，由于气泡体积继续增大，气泡受到的浮力随之增大，因此气泡被迅速拉高。同时气泡底部基圆半径和接触角也随之迅速减小，气泡受到的壁面附着力也随之减小，因此气泡在很短的时间内脱离加热表面。

2.2 基于气泡动态参数的近壁面处相变机理分析

池沸腾过程中界面处的传热包含多种传热机理，包括微液层的蒸发，大液层以及热边界层外气液界面的蒸发和自然对流等[30]。自然对流一般发生在气泡投影面积外侧，而相变过程则主要发生在气泡底部的微液层和大液层区域。气泡基圆半径定义为气泡中心到气泡底部气液界面与加热表面接触点的距离。所在位置为微液层与大液层的分界点，如图1所示。基圆半径Rb的变化可以从实验中直接测得，而热边界层厚度δt则可用式(7)计算[31]：

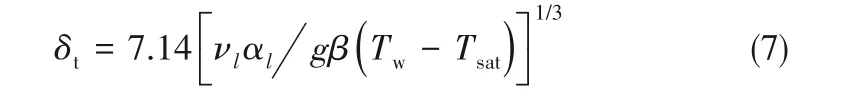
式中，g为当地重力加速度，νl、αl、β分别为液体工质运动黏度、热扩散率、体积膨胀系数，Tw和Tsat分别为加热表面温度和工质饱和温度。

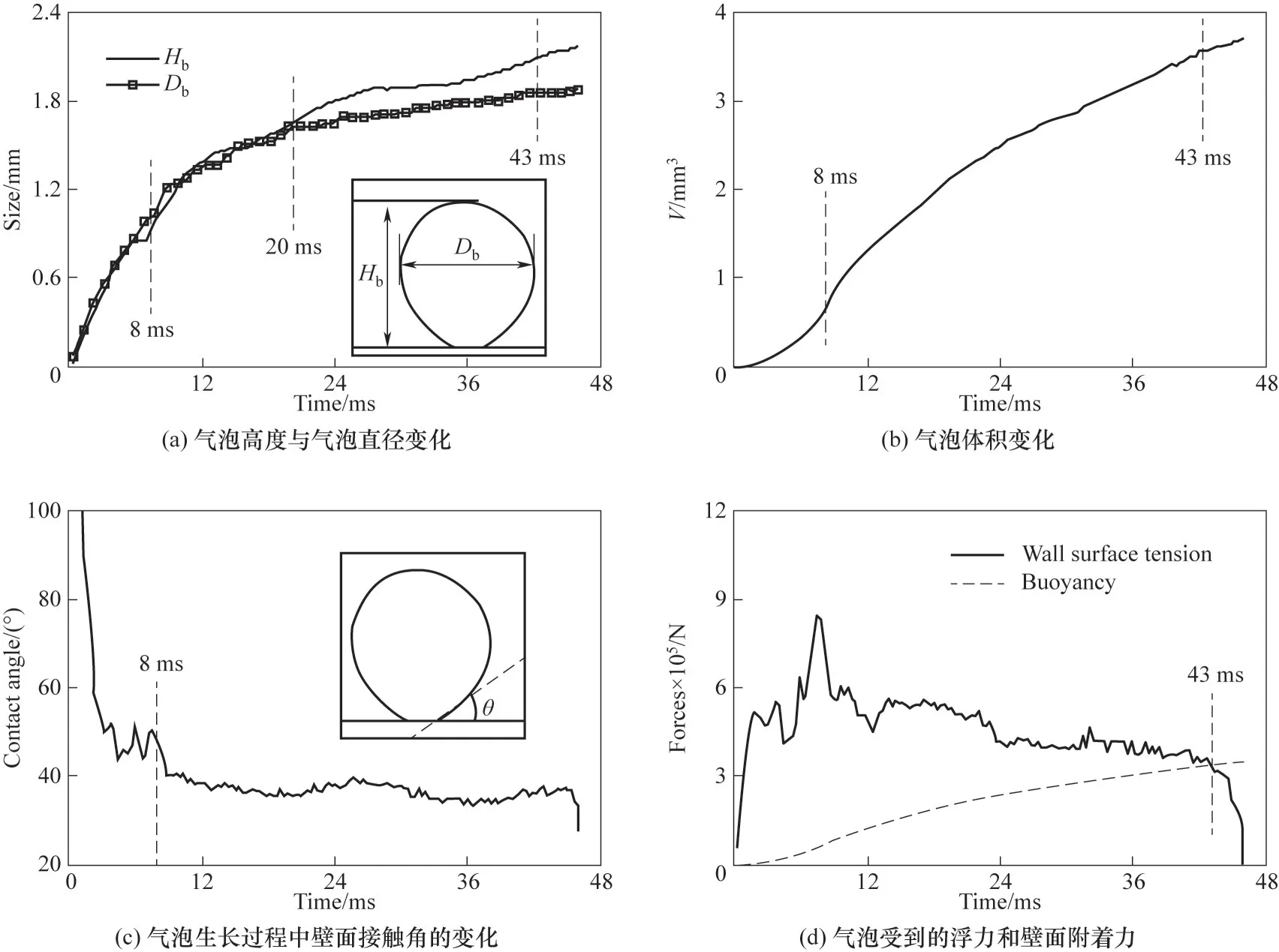
图6 气泡生长过程中气泡高度、直径、体积、接触角以及浮力和表面张力随时间的变化(ΔT=4.82 K)Fig.6 The variations of bubble height,diameter,volume,contact angle,buoyancy and surface tension with time during the bubble growth period

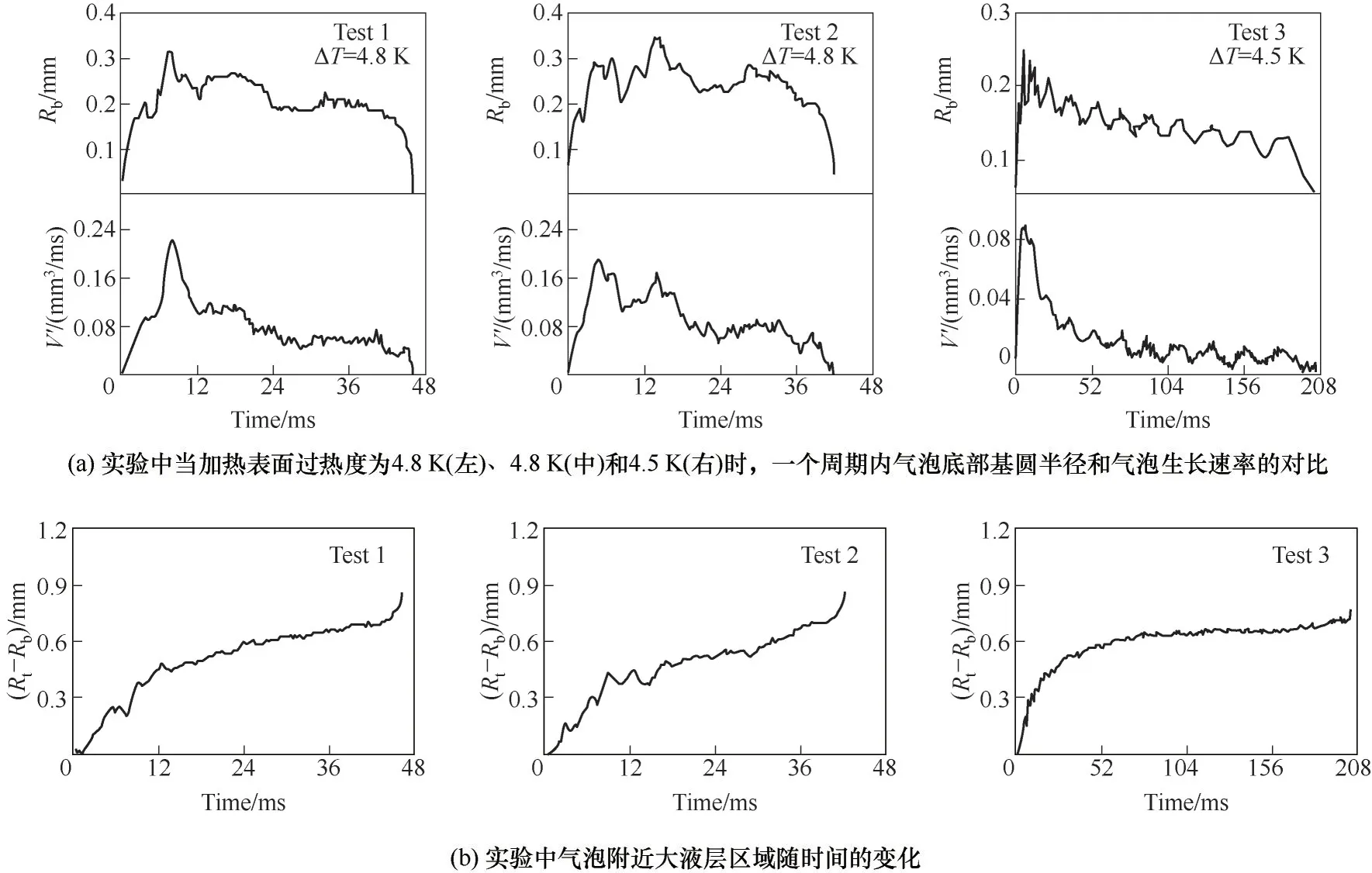
图7 实验中测得的气泡生长速率、气泡底部基圆半径和大液层区域随时间的变化Fig.7 Comparison of the bubble growth rates with the bubble root radii and macrolayer regions measured in the experiment

为进一步探究沸腾过程中尤其是在气-液-固三相共存的热边界层内的相变机理，实验中对三组不同气泡生长过程中的基圆半径Rb和大液层区域(Rt-Rb)的变化进行了分析，如图7所示。可以看到，三组数据中气泡基圆半径均在气泡生长初期迅速增大，随后呈现一定的波动，而在气泡脱离前则快速减小；而大液层区域主要与热边界层内的气泡尺寸相关：随着气泡体积的逐渐增大，大液层区域在气泡的整个生长过程中均呈现增大的趋势，在气泡脱离前达到最大。可以看到，气泡生长过程中微液层区域与大液层的变化趋势截然不同。因此，通过对比分析气泡生长速率与实验中气泡基圆半径、大液层区域随时间的变化可定性地判断微液层区域与大液层区域在气泡生长中的贡献，即，倘若大液层的蒸发是气泡生长最主要的蒸汽来源，气泡的生长速率应该与其变化规律基本一致；若微液层蒸发占主导，则气泡的生长速率应该与基圆半径变化规律相近。

进一步，通过实验中气泡体积变化可以得到气泡的生长速率V′，如图7(a)所示。对比分析气泡生长速率与实验中气泡基圆半径、大液层区域随时间的变化，可以看到，气泡生长速率并不随着大液层区域的增大而增大，而与气泡基圆半径的变化趋势基本相同：当气泡基圆半径增大时，气泡生长速率随之增大，反之亦然。进一步利用相关性公式(8)计算气泡生长速率与基圆半径和大液层半径的相关性，可以得到图7的三个周期中气泡生长速率与大液层区域变化两组数据之间的相关系数分别为-0.1965、-0.3195和-0.4554，其中负号表示二者呈现负相关；而与气泡基圆半径变化之间的相关系数分别为0.8017、07654和0.7451。

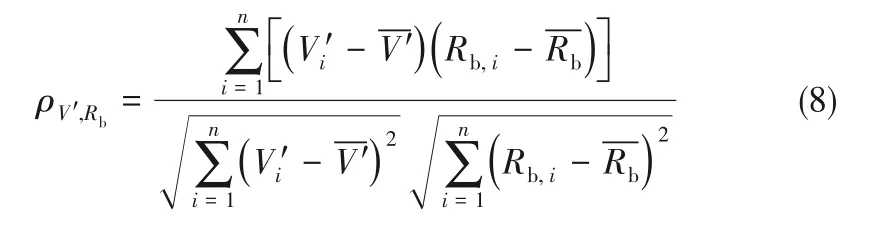
因此，可认为气泡生长速率的变化与基圆半径的变化呈现显著的正相关，这表明孤立气泡沸腾过程中的相变换热主要发生在基圆半径内侧即微液层区域内，而大液层区域的蒸发在当前实验工况下则贡献较少。

2.3 基于孤立气泡沸腾过程中宏观参数的微液层厚度预测

2.3.1 沸腾换热模型 既然气泡底部的微液层蒸发是孤立气泡沸腾过程中最重要的换热机制，其厚度动态变化则成为理解沸腾过程的重要参数。由于其尺度相对较小(一般小于50μm)，厚度通常难以直接观测，实验中通常借助激光干涉等技术对其进行测量[18-19]。本文尝试结合数值模型，通过匹配实测的气泡生长速率，来对气泡生长过程中底部微液层的厚度进行预测。由于加热器关于中心轴线严格对称，汽化核心位于其顶面中心处，计算中采用5°的二维轴对称楔形区域作为计算区域，如图8(a)所示。区域的半径设置为5 mm，高7.5 mm。加热器内热传导控制方程为：

式中，T为加热器内温度分布，αw为固体的热扩散系数，对于铜材料为1.14×10-4m2/s。计算域内侧为旋转轴，模拟中采用对称边界，外侧为隔热层，忽略其换热。底部根据实验结果设置为固定温度。计算域上表面为加热表面。汽化核心正下方2.5 mm处设置有温度观测点，模拟中用此点的计算温度与加热器内的温度变化实测值进行匹配。

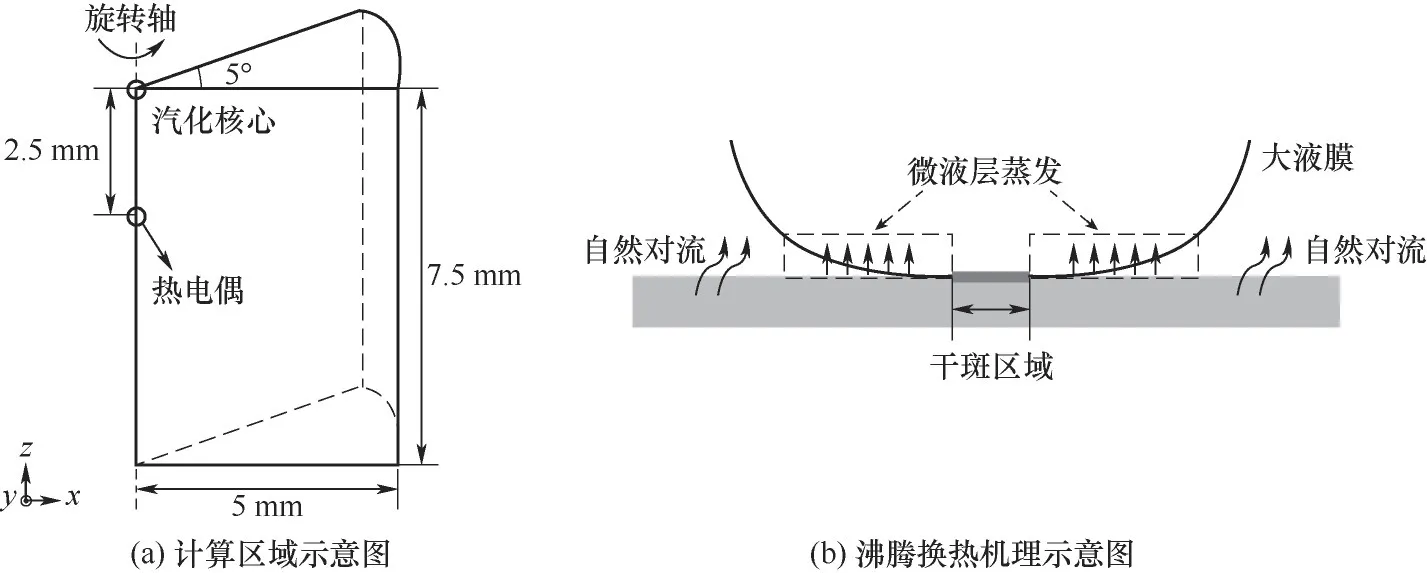
图8 计算区域和沸腾换热机理示意图Fig.8 Schematics of the calculated domain and the heat transfer mechanisms on the boiling surface

对于加热表面上热边界层内的换热，根据实验中气泡界面在不同时刻的不同位置，模拟中将其划分为三个区域,由气泡中心向外依次为干斑区、微液层区和自然对流区，如图8(b)所示。其中，气泡基圆半径外侧为自然对流区，基圆半径的位置则由实验测量结果确定。而在基圆半径Rb以内，加热表面由微液层覆盖，微液层区域中心最内侧为干斑区域。Gao等[18]通过激光干涉法对乙醇气泡沸腾过程中干斑区的演化进行了测量，结果表明，在微液层蒸干前，干斑区域半径随着气泡生长时间的推移呈现对数变化，其他相关实验[17,19]与模拟结果[32]也基本支持这一结论。同时在气泡生长后期，由于气泡底部基圆半径发生收缩，三相区域内会出现较为明显的横向回流[6,33]，导致加热表面被重新润湿，如图5(c)所示，干斑区域随之减小。根据Jiang等[24]的模拟结果，液层的回流速度与基圆半径的收缩速度基本呈正比例变化，因此，模型中液层回退的距离为：

式中，Rb,0和Rd,0分别为上一时刻的基圆半径和干斑区域半径。当气泡脱离时，干斑区域半径与基圆半径重合，微液层完全蒸干，微液层区域为0。据此，可以假设干斑区域变化为：

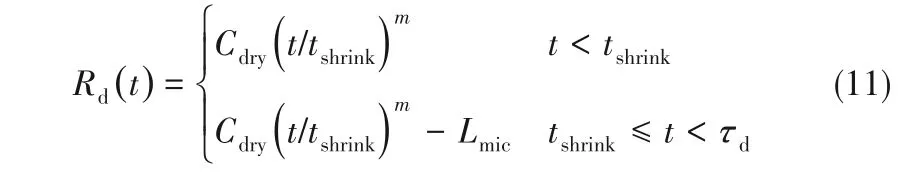
式中，τd为气泡脱离时刻，tshrink为基圆半径开始迅速收缩的时刻，可根据气泡受到的浮力与壁面的附着力来确定[图6(d)]；Cdry和m为根据实验数据拟合得到的经验参数，其取值与工质物性、壁面过热度、壁面润湿性等因素有关。对于m的取值，Gao等[18]给出的参考值为0.6～1.2之间。微液层存在区域为气泡底部三相接触线到基圆半径之间，因此微液层区域半径为：

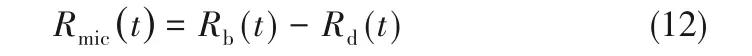
模拟中加热器上表面的热通量根据各区域上的换热状况确定。在气泡中心最内侧的干斑区域，加热表面直接与过热蒸汽相接触，换热量很小，忽略不计。而在微液层蒸发区，加热表面的热量通过热传导进入微液层，液层在气液交界面位置蒸发产生蒸汽。根据热平衡原理，微液层蒸发消耗的热量与热传导进入气泡的热量相同，可根据傅里叶导热定律计算[34]：

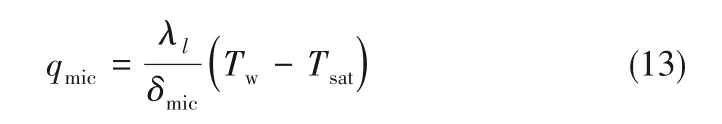
式中，Tw为加热表面温度，Tsat为饱和液体温度。而在微液层外侧，由于气泡与加热表面之间的液体较厚，热量从加热表面直接传递进入主流体中，其热通量根据Holman自然对流关系式评估[35]：

式中，Tw(r,t)为t时刻加热表面上r处的温度；Rd为干斑区域半径，即三相接触线位置；Rb为气泡基圆半径，即微液层最外侧。

由于干斑区域和自然对流区域不发生相变，因此这个过程中产生的蒸汽量(由此可计算气泡生长率)可根据微液层的蒸发量来确定，即[36]：式中，Hfg为汽化潜热，ρv为蒸汽密度。

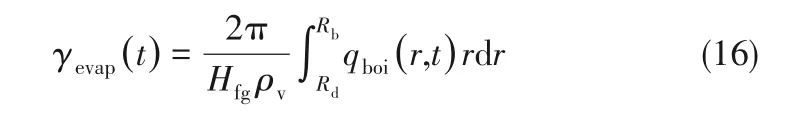
2.3.2 微液层厚度的预测 由于微液层的分布在目前实验中无法直接测定，根据陈宏霞等[12]的实验结果，计算中初步假定其厚度均匀。其取值需要在计算中进行多次迭代匹配来确定，计算过程如图9所示。模拟前首先给定微液层厚度的初始值，范围为1～5μm。根据预设的微液层厚度结合实验中测定的气泡动态参数通过式(15)可计算得到加热表面的热通量，以此作为加热表面边界条件进行加热器的导热计算则可获得当前时刻的加热表面温度分布。迭代多个周期直至计算中加热表面温度达到稳定时，根据式(16)可计算得到一个周期内的蒸汽产生量和气泡生长率并与实验所获气泡生长率进行比较，若与实验不符合，则调整液层厚度进行下一迭代步的计算。气泡生长率误差函数设置为：

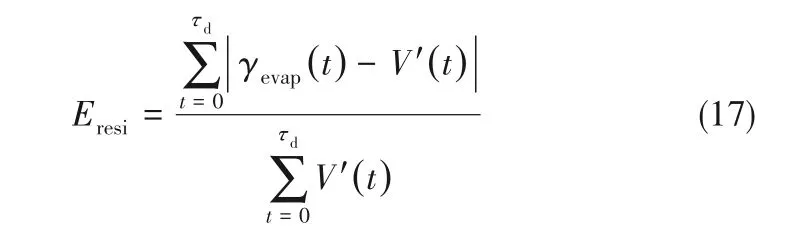
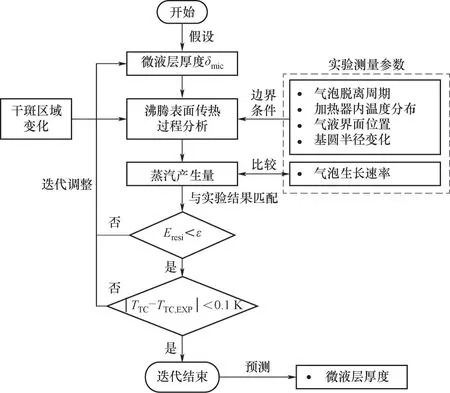
图9 加热表面传热计算与实验测量参数间的迭代匹配策略Fig.9 The matching strategy between the simulation of boiling surface heat transfer with the measured bubble dynamics

根据误差函数计算结果，采用二分法调整预设的微液层厚度重新进行多个周期的迭代计算，直到计算得到的蒸汽产生量与实验结果间的误差函数小于预设的最小值ε。另一方面，也比较模拟中热电偶测点位置处的温度与实验测得的结果，当误差在0.1 K以内时认为与实验结果相符，迭代完成，此时的微液层厚度即为当前实验条件下的预测结果。2.3.3 模拟结果 基于OpenFOAM平台3.0.x版本下的laplacianFoam求解器对加热器内部温度场[式(9)]进行求解。采用有限体积法对控制方程进行离散，非稳态项采用隐式离散，扩散项采用中心差分进行离散，矩阵求解选用预处理共轭梯度法。计算开始前首先将加热器上表面边界条件设置为自然对流，热通量由式(14)决定，下表面过热度根据实验测量值固定为4.95 K。时间步长设为0.3125 s。

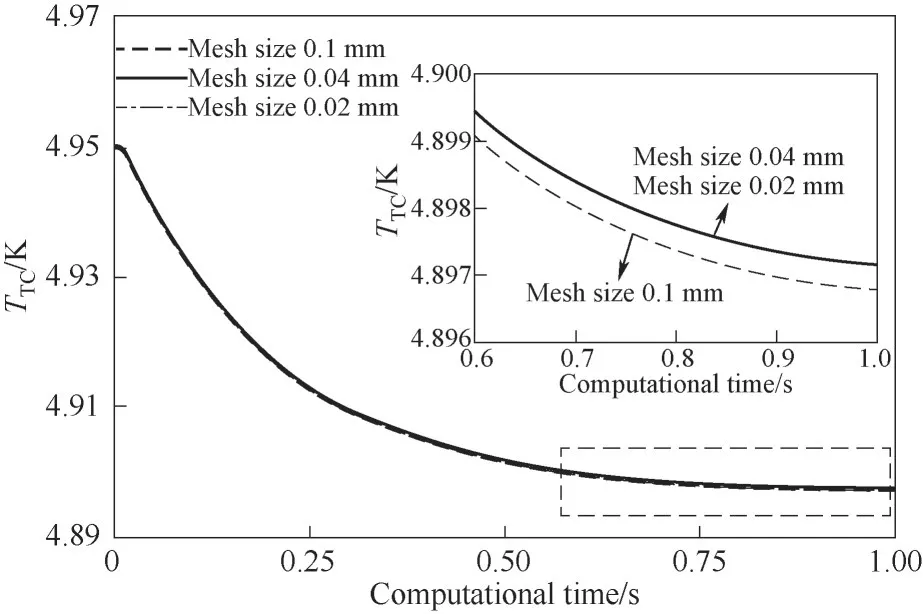
图10 不同网格数量下热电偶处的过热度变化Fig.10 The local superheat at the position of thermal couple T TC in simulations with different mesh sizes

分别采用50×60、125×150和250×300三种不同数目的网格对加热表面上的自然对流换热过程进行了模拟，其对应最小网格尺寸分别为0.1、0.04和0.02 mm。图10给出了三种网格下模拟中热电偶位置处的过热度TTC的变化。可以看到，当网格尺寸为0.1 mm时，热电偶处的过热度略小于网格加密后的计算结果，而当网格尺寸为0.04 mm时，计算结果不再随着网格的加密而发生变化。因此，模拟中最终将计算区域划分为125×150个网格。此外，在1.0 s时过热度逐渐趋于平缓，从0.9 s到1.0 s过热度降低小于10-3K，因此认为此时换热过程已经达到稳态。模拟中将此时的加热器内的温度分布作为初始场进行加热表面的换热计算。

图11 气泡底层基圆半径、干区和微液层区域半径变化的模拟结果Fig.11 The simulated variations of bubble root,dry area and microlayer region radiiwith time

根据干斑区域计算公式(11)，结合所测一个周期内气泡基圆半径，可得干斑和微液层区域的变化如图11所示。其中右上角插图给出了气泡基圆半径Rb，干斑区域半径Rd和微液膜区域半径Rmic的位置关系。经过多次迭代计算后，模拟中最终得到的微液层厚度为3.43μm，与文献[8,18-19]的结果基本吻合。此时计算得到的一个周期内气泡生长速率如图12所示，与实验结果的相对误差为22%。可以看到，与实验结果相比，模拟得到的气泡生长速率基本合理。这也进一步表明微液层在孤立气泡的沸腾过程中起主导作用。

图12 气泡生长速率的模拟结果和实验结果的对比Fig.12 The comparison of the simulated and experimental bubble growth rate

图13则给出了模拟过程中加热表面的平均过热度以及热电偶位置处的过热度随计算时间的变化。在经过20个气泡周期的换热计算后，加热表面温度变化基本达到稳定，平均过热度约为4.82 K。由图13(b)可以看出，稳定后加热表面在一个周期内的温度变化与微液层区域的变化密切相关：当微液层区域增大时，加热表面平均温度降低；而在气泡脱离前，随着微液层区域的迅速减小，壁面温度迅速升高。模拟中得到的汽化核心下方2.5 mm处热电偶的过热度TTC基本在4.87～4.88 K范围内波动，与实验参考值4.88 K基本相符。

图14给出了气泡生长不同阶段内不同时刻加热表面上的过热度分布。可以看出，在气泡生长初期的8 ms之内[图14(a)]，加热表面温度基本呈现下降趋势，而在气泡生长后期[图14(b)]逐渐恢复到初始状态。其中，加热表面中心位置温度波动最为剧烈：在前8 ms内，由4.83 K迅速降低到4.28 K；随后由于干斑区域的出现，其温度逐渐回升。相比之下，距离汽化核心较远的位置则波动较小。图中“○”表示该时刻的三相线位置，其内侧为干斑区，外侧为微液层区域；而“◆”则表示该时刻的基圆半径位置，其外侧为自然对流区域。可以看到，加热表面上的最低温度出现在两标记之间的区域即微液层覆盖区；在更内侧的干斑区域，加热表面与过热蒸汽直接接触，因此温度较高；而在外侧的自然对流区，由于无相变发生，换热较差。因此，气泡底部最终形成以三相接触线和气泡基圆半径为边界的环形低温带[11,37]。

模拟中通过与实验得到的气泡生长速率进行匹配，间接得到的气泡底层微液层厚度为3.43μm。其他研究者直接测量得到的微液层厚度分别为:1～4μm(Zou等[8])，3μm(Jung等[19])，4μm(Gao等[18])，本研究得到的微液层厚度在合理范围。本文的预测结果进一步验证了微液层蒸发机理。对于铜表面上初始液层厚度斜率Cslope[16]的取值，在过热度为5 K左右时，本文采用的参考值为0.02～0.03，与Sato等[25]的推荐值0.0245基本相符。

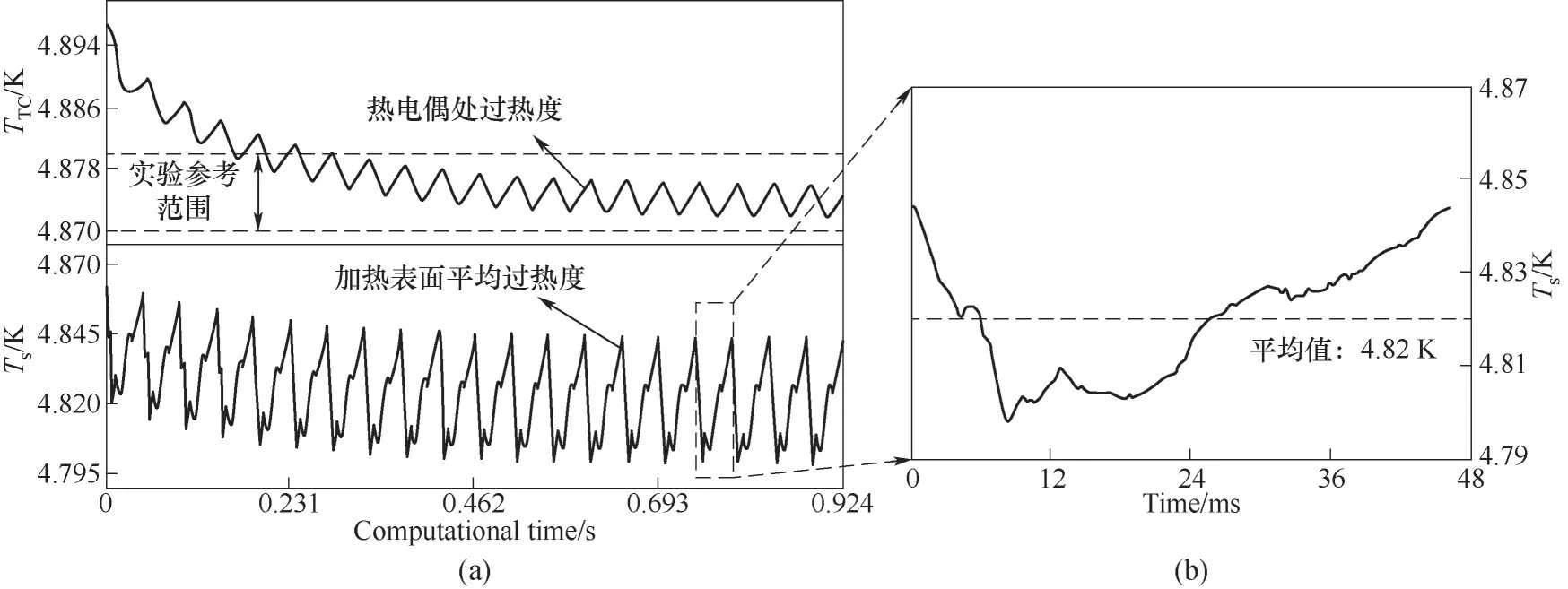
图13 加热表面及加热表面以下2.5 mm处过热度随时间变化的模拟结果(a)和一个周期内的加热表面过热度随时间的变化(b)Fig.13 The simulated variations of the mean superheat on the heated surface and thelocal superheat at the position of 2.5 mm below the surface(a)and the mean superheat of heated surface within one bubble period(b)

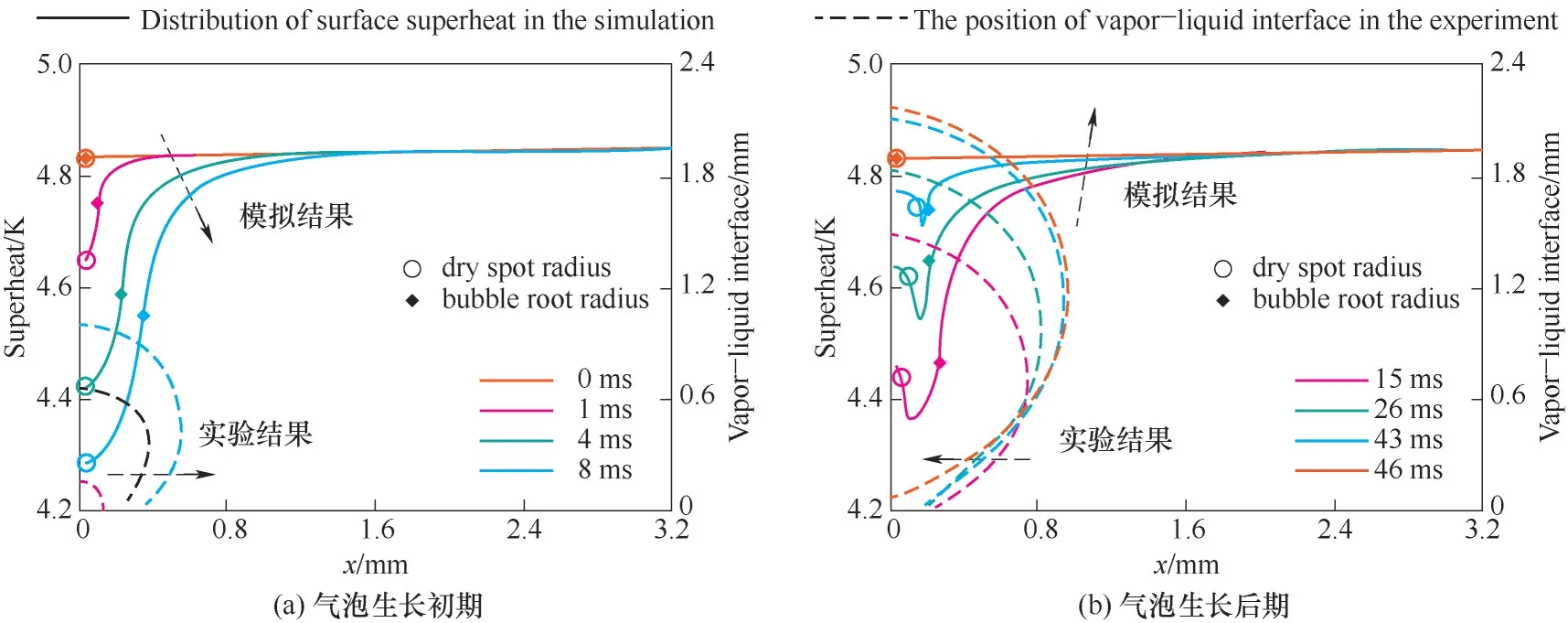
图14 气泡生长过程中不同时刻加热表面过热度分布的模拟结果及气泡界面位置的实验结果Fig.14 The superheat distributions of the heated surface in the simulation and the positions of bubble interface of the experiment at different moments

需要说明的是，本文研究仅针对较低热通量(约5.5 kW/m2)下的孤立气泡沸腾区域，在此区域内，微液层的蒸发在沸腾换热过程中起主导作用。但随着热通量增大，微液层蒸发作用在气泡生长过程中所占份额会逐渐减少，而大液层以及主流体中两相界面部分的蒸发所占的份额会逐渐增加。在气泡水平合并频繁的高热通量区域(1.0 MW/m2以上)大液层的蒸发将成为换热的主要机理[9,38]。不同热通量区域的沸腾换热机理和气泡动力学特性还需通过实验和多物理场耦合分析进一步考察。

3结 论

本文首先通过单个气泡沸腾实验获得了气泡生长过程时间序列图像，进一步对气泡生长过程图像进行图像处理，获得了气泡生长过程中的接触角、基圆半径、体积、高度和直径等动态参数变化。相关性分析结果表明，气泡的生长速率与气泡底层基圆半径的变化显著相关，由此可认为基圆半径内侧的微液层蒸发是孤立气泡沸腾过程中最主要的相变机理。在此基础上，结合实验测得的气泡动态参数建立了加热表面的换热分析模型，通过迭代匹配实验测得的气泡生长速率和加热表面过热度最终得到，当加热表面过热度为4.82 K时，气泡底层微液层的厚度约为3.43μm。液层厚度预测结果与相关实验测量值吻合，表明低热通量孤立气泡沸腾过程中微液层蒸发是气泡生长的主要机理，这为进一步进行沸腾过程流热耦合分析和沸腾换热表面设计奠定了理论基础。

符号说明

Cdry——干斑区域演变经验参数，m

Cslope——微液层初始斜率

cp,l——液体比定压热容，J/(kg·K)

D——气泡横向尺寸，m

Db——气泡直径，m

Eresi——迭代残差

Fb——浮力，N

Fσ——壁面附着力，N

g——重力加速度，m/s2

Hb——气泡高度，m

Hfg——汽化潜热，J/kg

I——通过加热棒的电流，A

Lmic——基圆半径收缩引起的微液层移动的距离，m

m——经验参数，取值范围0.6～1.2

Rb——基圆半径，m

Rd——干斑区域半径，m

Rmic——微液层区域半径，m

Rt——热边界层与气泡界面接触点位置，m

q——平均热通量，W/m2

qboi——加热表面的局部热通量，W/m2

qmic——微液层蒸发的热通量，W/m2

qnc——自然对流的热通量，W/m2

r——距离气泡中心的距离，m

T——温度，K

Ts——加热表面平均过热度，K

Tsat——工质饱和温度，K

TTC——热电偶位置过热度，K

ΔT——加热表面过热度，K

t——时间，s

tshrink——基圆半径开始迅速收缩的时刻，s

U——加热棒两端电压，V

V——气泡体积，m3

V′——气泡生长速率，m3/s

z——高度，m

α——热扩散系数，m2/s

β——体积膨胀系数，1/K

γevap——蒸汽产生率，m3/s

δt——热边界层厚度，m

δ0——初始微液层厚度，m

ε——迭代相对误差

θ——接触角，(°)

λ——热导率，W/(m·K)

μ——动力黏度，N·s/m2

ν——运动黏度，m2/s

ρ——密度，kg/m3

ρxy——相关系数

σ——表面张力系数，N/m

τd——气泡脱离时刻，s

下角标

l——液体

v——蒸汽

w——固体表面

0——上一时刻参数