基于一种优化权重的K-近邻算法的缺失财务数据组合填补
2021-06-03冯长焕侯世君
文 雯,冯长焕,侯世君
(西华师范大学 数学与信息学院,四川 南充 637009)
0 引言
根据《中华人民共和国会计法》的规定,上市公司每季度需报送资产负债表、损益表、现金流量表三大主表.根据这些财务数据就可以得到相应的财务比率指标,如反映企业的盈利能力的指标有每股收益、每股净资产等,反映企业的偿债能力的流动比率、速动比率等,反映营运能力的应收账款周转率、存货周转率等,反映成长能力的主营利润增长率、净利润增长率等财务比率指标.这些数据对于研究上市公司的财务状况和经营状况,以及评估上市公司的综合能力具有相当重要的参考价值.但部分公司在报送这些数据时会产生数据缺失.股东、债权人或是企业相关决策者以及政府管理部门都需要用这些数据进行分析.如果这些数据缺失,会导致相应的指标信息同时丢失,用这些缺失的数据作分析得到的结论便会出现偏差.
综上,缺失数据填补成为热门研究对象.研究者提出许多数据填补方法:全局常量填补(global constant)和均值填补法[1],两种方法分别使用全局常量和缺失属性的均值对缺失字段进行填充,大多数情况下,这两种方法会得到有偏的结果;热平台填补法[2](hot deck imputation),在当前完整数据集中找一个与含有缺失值的变量相似的样本,用其值进行填补;冷平台填补法[2](cold deck imputation),该方法与热平台填补法的不同点在于,从完整数据集以外数据集找到相似样本.常用的方法还有回归填补法(regression),期望值最大化方法(expectation maximization,EM)等.
除上述方法以外,还可以利用机器学习算法填补缺失数据,减小填补误差.如基于神经网络[3]、贝叶斯网络[4]、聚类[5]、K-最近邻(K-Nearest Neighbor,KNN)算法[6]、关联规则[7-8]的缺失数据填补算法等.
KNN算法在理论上较为成熟,是最简单的机器学习算法之一,利用相关性测度思想填补缺失值是可行的.
1 相关概念
1.1 明考夫斯基距离
明考夫斯基距离(明氏距离)[9]是在聚类分析中产生的点间距离(即样品与样品之间的距离),是基于定量变量的距离测度.记xi=(xi1,xi2,…,xip)与xj=(xj1,xj2,…,xjp)是样品i与样品j的观察值,则明氏距离定义为
(1)
其中dij表示样品i和样品j之间的距离,q表示阶数,k表示每个样品的指标数,k=1,2,…,p.根据q取值的不同,明氏距离可分为曼哈顿距离、欧式距离和切比雪夫距离等.
当q=1时,一阶明考夫斯基距离称为绝对值距离或曼哈顿距离:
(2)
当q=2时,二阶明考夫斯基距离称为欧几里得距离或者欧氏距离:
(3)
当q→∞时,明考夫斯基距离可以转化为切比雪夫距离:
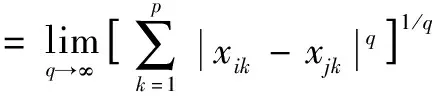
(4)
在各个领域,明考夫斯基距离都有应用,如在机器学习中向量距离问题的处理便利用了曼哈顿距离和切比雪夫距离,在多元统计分析中通过欧氏距离定义样本均值之间的距离,在优化KNN算法中将用来寻找相似样本.
1.2 K-近邻算法分类思想
K-近邻算法[10]虽然依赖于极限定理,但在最后作分类决策时只和极少量的相邻样本有关.其思想为:给定一个训练数据集.对于一个新样本,首先通过欧氏距离找出该样本的K个最近邻居,若这些邻居多数又与该样本属于同一类,就把这个样本分到这个类中[10].
1.3 结合K-近邻算法的回归应用
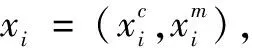
(5)
2 一种优化权重的K-近邻算法——OKNN算法
当样本间的距离很接近时,上述的KNN算法回归应用在数据填补中效果不理想,应对距离和权重进行优化改进,得到优化权重的KNN算法.
2.1 相似性度量改进
在进行度量之前,需要对数据进行标准化处理,消除量纲的影响,并且在样本不平衡时,可以避免大容量样本比小容量样本的属性权重过大.将不同阶数的明考夫斯基距离分别进行试算,选出相似样本,对距离进行组合加权得到相关系数,应用相似样本对应指标填补缺失值.由文献[12]知三阶明考夫斯基距离填补效果最好,所以采用三阶明考夫斯基距离进行距离度量:
(6)
2.2 K值的选取
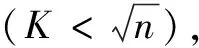
(6)
计算得到n-1个明氏距离,给出集合
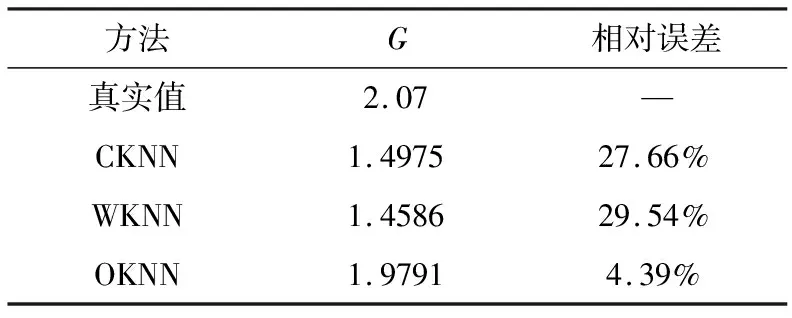
DK={Dij||Dij-Dmin| (7) Dmin为最小的三阶明氏距离,集合DK={d1,d2,…,dm},则m=K,从而确定K值.当得到距离与Dmin非常接近时,集合为 DK={Dij||Dij-Dmin|<αDmin} (8) α为距离调整系数,取值范围为(0,1],当α=1时即为公式(7),通常α取0.1. (9) K为相似样本个数. 为避免距离的倒数作权重出现的误差,选中距离相差不大的相似样本分析比较,利用OKNN算法,说明了新算法的有效性和可行性. 实验数据选取股票代码从000988(华工科技)至代码002069(獐子岛)2018年年报数据的营运能力指标,此实验数据共83个样本,7个指标:应收账款周转率、应收转款周转天数、存货周转率、存货周转天数、固定资产周转率、总资产周转率、净资产周转率,分别记为A、B、C、D、E、F、G.具体数据见表1. 表1 2018年各公司营运能力指标 为了验证新算法的有效性和填补准确性,先选取对应指标完备的数据集.随机选取一个样本中任意一个指标,令其缺失.例如,令第56个样本即代码002042(华孚时尚)的G指标(净资产周转率)数据缺失,接着分别用经典KNN算法(简记为CKNN),加权平均的KNN算法(简记为WKNN),优化权重的KNN算法(简记为OKNN)对缺失值进行填补. 表2 不同方法对缺失值填补情况 由表1可知,当与相似样本距离相近时,用优化权重的KNN算法填补效果更优,误差更小,从而证实了结合优化权重的KNN算法的有效可行性. 上述基于KNN算法的优化权重算法,避免了直接用距离的倒数作为权重可能出现的一些误差,使得填补的缺失值更接近真实值,为财务数据的填补提供了一种新方法.这种方法对相似样本的缺失值填补效果较好.2.3 基于KNN的组合优化权重
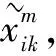
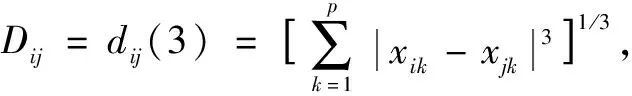
3 实例与分析

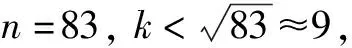
4 结论
