基于桩端和桩侧阻力相互作用的超长桩承载力研究

熊玉铭，何永曦，潘 浩

(四川省第三建筑工程有限公司，四川 成都 610051)

近年来，大型港口水利工程项目、高层楼房建筑、大型桥梁施工等工程建设中广泛使用大直径超长桩体，这给传统的桩基稳固方法带来了新的机遇和挑战。而目前已有的研究资料(文献[1-3])表明，当其桩顶部位置的承载水平面临极限挑战时，超长桩的桩端位置附近所感受的摩阻力会出现陡增的现象，但在不同抗滑桩周围土体强度和桩土作用面特性的综合因素影响下，这种增强程度也不尽相同。国内外很多学者对此也进行了大量研究。其中，文献[4]详细探讨了对软质土体地基的超长桩开展静载试验过程，并获得抗滑桩的预应力测试结果并予以分析。通过数据结果可发现，基于高荷载环境下超长抗滑桩反映为端承摩擦型桩，且抗滑桩的端阻力和侧阻力间互为作用且不能同步发挥。文献[5]对温州地区某工程抗滑桩超长钻孔灌注的桩静载试验进行了详细探讨，并根据数据结果来分析软质土体地基超长桩的荷载传递原理。文献[6]结合自平衡原理，对苏通大桥测试桩端后的压浆效果进行静载试验分析，以此探讨桩端压浆操作前后的承载力特性。文献[7]详细分析了测试桩体的压浆资料数据，发现测试桩端的压浆效果可以通过桩周土体的接触面特性进行改善，从而提高测试桩侧的摩阻力。文献[8]详细探讨了在抗滑桩周围土体强度较高环境下的桩静载试验过程，并得出在桩岩位置发生相对位移较小的基础上，抗滑桩的端阻力和侧摩阻力可以发挥出较好的水平。

由上述文献可以看出，在抗滑桩的桩端注浆可以改善超长桩的承荷力度，但桩端阻力和侧阻力是作为独立变量进行分析的，并将二者结合起来开展研究的资料较少。文献[9]详细探讨了不同桩端土环境下的软质土体地基中超长桩的承荷力传递原理，得出了抗滑桩的桩身形变规律、端阻力和侧摩阻力间的作用规律。文献[10]通过实验室和工程现场桩静载实验相结合的方式，探讨了桩周土在荷载传递中的作用过程，并深入剖析了桩端阻力和侧阻力相互作用的原理。

总体来说，上述文献研究对超长桩的承载特性及桩端阻力和侧阻力的相互作用机理给出了具体论述，在理论建模和工程实践方面均有了可行依据。在此基础上，本文在对超长桩体的承载性能方面采用“弹性理论方法”进行求解计算，其方法是以作用于桩体各向同质弹性半空间内某点的集中受力形成的Mindin解的条件下，按照桩体—土体位移相互协调作用基础上建立静载受力方程。而对于桩基施工现场环境所遇到的土体质度，通常情况下不能完全满足均匀弹性体的条件，其结构大多呈层状分布，仅依靠Mindin求解方法可能会产生很大的误差。文献[11-12]基于桩土呈层次性的条件下，提出了广义弹性理论下Mindin求解方法，考虑桩—土相对滑移的情况下附加非弹簧模型，并在桩基中计算端阻力和侧摩阻力过程中结合“线性形变分层法”来改进地基静载测试过程中土变模量和泊松比，将“有限单元法”和虚功原理[13]进行整后求解弹性半空间内的节点荷载，以此来适应不同桩长分段求解和提高计算精度。

综上所述，本文以分析复杂介质环境下的单长桩基为基础，将广义弹性原理和优化反分析理论进行结合，可计算复杂介质中的超长桩摩擦型单桩的承载机能和测试静载试验的沉降曲线。另外，通过测试得到的桩周和端土力学数据，结合有限单元法对超长桩桩端和桩侧阻力的Mindin解进行修正计算，以此提高抗滑桩的桩端和侧阻力相互作用的计算精度，并通过某桩基工程实例论证本文所提方法的合理性。

1 桩土相互作用的受力模型

1.1 桩土地基建模和土位移方程

将线性变形层的桩土地基某分层i的土变形变模量设定为Ei，泊松比设为vi，桩端以下到刚性层顶部的参数设定为Eb，vb。桩身穿越层平均模量设定为Em，而对于成土层。本文可设定：

(1)

对于摩擦型的单体桩，桩端受力层土的弹性模量Eb和桩身穿越层平均模量Em的比值低于设定值RE时，应以桩土地基的线性形变层进行模拟，桩—土界面选择非线性弹簧模型进行仿真模拟。桩基线性分层模型如图1所示。

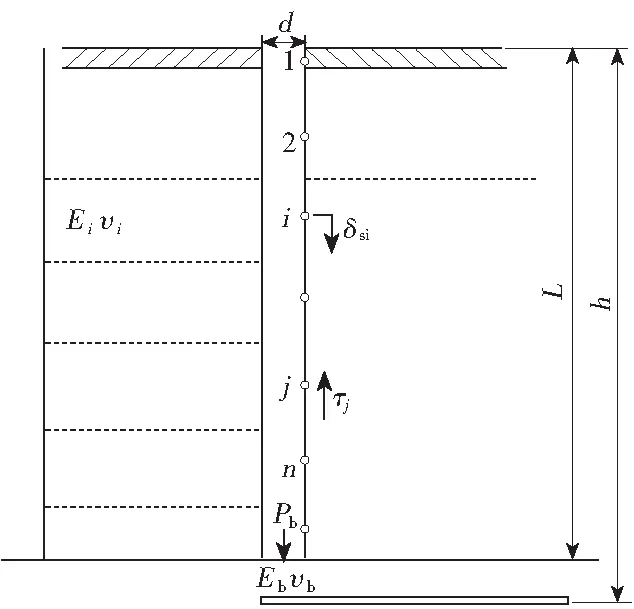
图1 桩基线性分层模型Fig.1 Pile foundation linearity becomes model

结合图1可知，相应结点的土位移δsj应为其下各土层的压缩量ΔSj之和，即：

(2)

通常情况下，单桩基于静荷载条件下其桩周无法及时排水固结，因此对黏土而言，其弹性模量E不取排水模量，v可取0.5；当超长桩体处于长期荷载环境下需要考虑排水固结的情况，弹性模量应取压缩量ES，v取0.25。且土层i的压缩变量ΔSi可为对应层的顶面和底面的位移差，即：

(3)

其中：

(4)

(5)

基于分析，可结合式(1)和式(2)写出沿桩身所有n+1个结点的桩土形变位移矩阵方程：

(6)

其中，

(7)

(8)

Γ=(τij)(n+1)×1

(9)

1.2 等效模量

为合理规避δij可能出现负值的情况，结合等效模量Esj进行修正：

(10)

式中，Ei为第i桩土分层的弹性模量。

由式(10)可看出，求解δij的值时，可选取j层以下的弹性模型按照原始模量计算，j层以上可利用等效模量计算。

2 桩土的竖向位移柔度矩阵

利用Mindlin[14]解，当各向同性弹性固体介质中存在任意集中力，可以求出半无限体中任何位置的应力、应变状态。如将土体看作各向同性弹性介质，利用其中求位移公式，可以近似求出土体中任意集中力对另一位置所产生的位移影响。桩基单元侧阻Mindlin积分如图2所示。

图2 桩基单元侧阻Mindlin积分示意Fig.2 Schematic diagram of Mindlin integral of lateral resistance of pile side unit

在图2中，单元j处侧面取一微元dF=dcds=dcd/2dθ，作用在该面积上的单位集中力为dP=1×dF。根据Mindlin求竖向位移的解，可以得出产生位移为：

(11)

式中，IP表示弹性半空间的内部j(0，0，+c)的点对应竖向作用力P造成的某内部坐标点i(x，y，z)的垂直位移影响因子，且：

(12)

(13)

其中：

(14)

可计算桩土第j分层区的桩侧摩擦阻力τj所引起的抗滑桩底部中心点处的位移，结合轴对称原理可得出位移影响因子：

(15)

因此，只需对式(14)和式(15)分别求积分，便可得到位移影响因子Iij和Ibj的值。

3 超长桩的桩土位移方程

考虑实际桩土地基分层环境可能并不是等分或者整分情况，本文采用综合虚功原理和有限单元法对桩体上的等效单元结点荷载分布求解。并结合单元土体刚度方程和结点等效荷载等参量推导出抗滑桩单元位移方程：

(16)

式中，各参数的具体表述意义见文献[15]。

因此，假定桩—土相对位移矩阵为：

δ=[δ1δ2…δnδb]T

(17)

即桩侧和桩端处对应的桩—土界面结点位移方程可如下：

δ=δP-δS

(18)

可将式(13)、式(16)、式(17)代入式(15)计算有：

(19)

4 桩侧和桩端非线性弹簧模型

将设置于各土层中电和桩端处的非线性弹簧来模拟桩侧和桩端土对桩的作用力分析，建立以桩侧土阻力和桩—土位移关系的非线性弹簧模型，如图3所示，即：

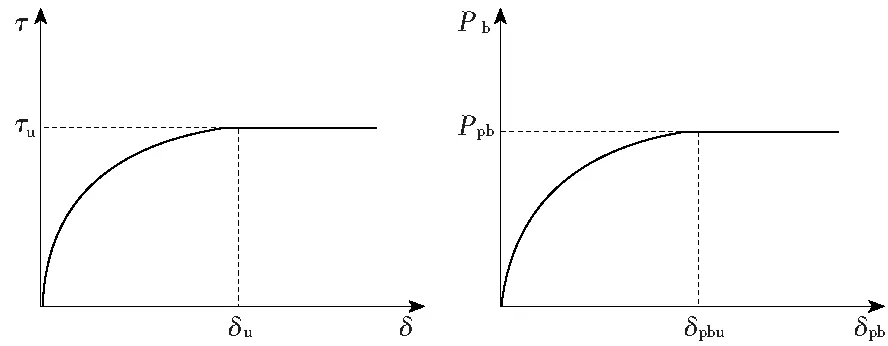
图3 桩侧和桩摩阻力示意Fig.3 Schematic diagram of pile side and pile friction

(20)

(21)

结合优化反分析方法，利用实测P—S数据曲线反推抗滑桩周围桩土层的侧摩阻力和桩底部的承载力。

5 算例分析

以某工程桩土基础为例，桩基础采用φ500 mm预应力桩体，并可根据地质勘测资料确定该抗滑桩基础工程为摩擦型单桩体结构，其荷载承受力设计值约为2 200 kN。本文取2根桩体进行静载试验测算分析，桩号分别取25号、35号。并设定超长桩入土深度分别为20.2、25.5 m，最大静荷载为3 530 kN。为了保证桩土参数更接近实际环境，可先对25号桩体进行优化反分析计算，即利用静载试验优化出的抗滑桩顶部界面和桩位的沉降关系，反演出抗滑桩体、周围环境和桩底土层的力学参数，并将得到的计算参数用于35号桩体的推演计算。具体结果如图4所示。

图4 35号桩体荷载—沉降曲线计算值和测试值对比Fig.4 Comparison effect of load-settlement curve calculated value and test value for No.35 Pile body

由图4可以看出，利用本文的广义弹性理论进行反演计算桩土的土质参数，可以看出35号桩的沉降曲线的计算数值和静载实测值吻合度很高，即说明了本文利用广义弹性理论对桩土静载试验进行反演计算的方法是合理的。

另外，对同一桩体的侧摩擦阻力进行分场景计算，可将抗滑桩顶部受力荷载设定为218、510、947、1 239 N等不同场景，则计算出的侧摩阻力实际值对比曲线如图5所示。

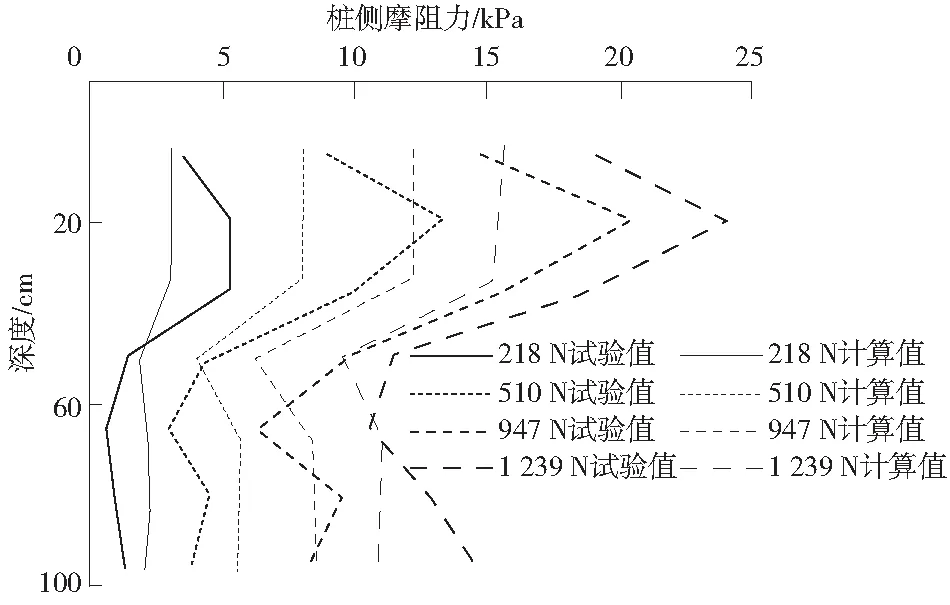
图5 桩侧摩阻力分布效果Fig.5 Distribution effect diagram of frictional resistance for pile side

由图5可知，利用广义弹性理论所计算的桩体侧摩擦阻力和实际试验值很接近，但靠近桩上部会存在一定偏差，且超长桩顶部荷载增加到1 239 N时，位于抗滑桩桩端部分的侧摩擦阻力会小于静载试验的实测值，原因在于超长桩侧土和桩端土的共同作用力形成的，这也是本算例探讨的重点。

(1)桩侧水平应力计算。计算当桩顶部荷载达到1 239 N时，超长桩的桩端摩阻力所引起的水平应力情况。计算结果如图6所示。

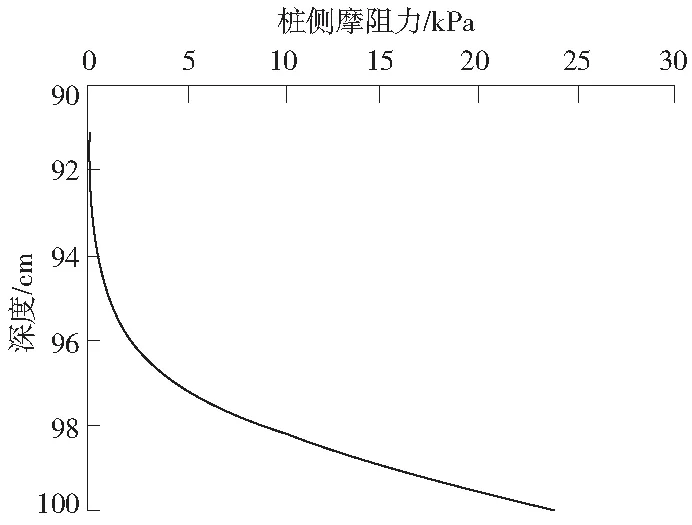
图6 桩侧水平预应力分布效果Fig.6 Horizontal pre-stress distribution effect diagram of pile side soil

由图6可看出，超长的桩端摩阻力在一定范围内会增强桩侧摩阻力，且随着深度的增加其相应的桩侧水平应力也相应增加。且从图中看出在91～94 cm内桩侧的应力水平增加缓慢，而在94～100 cm内其对应的应力水平增加较快，这充分说明了该区间范围对应的超长桩的桩端摩阻力能对桩周应力水平产生重要的影响。

(2)极限摩阻力增长值。根据图6所对应的抗滑桩在91～100 cm内的桩端摩阻力产生的水平应力情况，可结合相关公式计算出抗滑桩的桩端位置增加的极限摩阻力，具体结果见表1。

表1 水平预应力和极限摩阻力的增加量Tab.1 Horizontal prestress and increasein ultimate friction

上述采用弹性理论计算出的超长抗滑桩分层摩阻力均为对应分层土体的平均摩阻力。为方便比较，将桩端荷载产生的桩侧附加摩阻力在桩长对应91～100 cm均匀分配后，可得到超长桩在对应91～100 cm内的极限桩侧摩阻力平均增加量为：

(22)

式中，Δτi为i桩段的侧阻力增加值；Li为i桩段长度；Δli为分割长度；Δτfi为极限摩阻力增加量。其中，Δτi=∑Δli×Δτfi

通过对比可看出，图7(b)对应的抗滑桩侧摩阻力曲线比单独弹性理论优化的结果更接近桩侧摩阻力的试验值，说明结合优化方法后的计算策略对提高超长桩的侧摩擦阻力准确度具有促进意义。

图7 修正前后的桩侧摩阻力分布Fig.7 Distribution of pile side friction before correction

6 结论

本文详细探讨了摩擦型超长桩单体模型受力情况，以此建立单桩型土体线性模型，并结合土体地基分层特点，对Mindin求解方法进行相应改进，得到了适用于复杂土体介质中摩擦型抗滑桩静载机理计算的“广义弹性理论”和Mindin解，可为抗滑桩土体基础设计提供相应方法。另外，利用弹性理论计算超长桩的侧摩擦阻力过程中，发现桩静荷载取值较大时，会出现超长桩端部位置的桩侧摩擦阻力和实际测试值存在较大的误差。为了弥补这一缺陷，本文直接对抗滑桩的附加侧摩擦阻力进行相关修正，通过算例结果可明显看出考虑桩体附加侧摩阻力修正后的计算结果和测试值吻合程度很高，从而说明了本文所述的方法对提高超长桩的桩端和侧阻力相互作用的计算精度，对指导工程施工具有很好的借鉴价值。