曲线坐标下多孔材料模型特征值问题的二阶双尺度计算方法

叶舒愉， 马 强， 胡 兵

(四川大学数学学院， 成都 610064)

1 引 言

在物理、力学和工程领域，很多问题在数学上都被归结为求解偏微分方程特征值问题. 对于此类问题，传统的数值方法仅考虑对宏观现象的模拟，难以揭示微观构造的特性，因而对于复杂的材料结构传统的分析方法不再适用. 于是，国内外学者展开了对多尺度方法的研究. 多尺度方法将问题划分为两类不同的区域：第一类是耦合区域，主要对微-纳米构件和材料在微-纳米尺度下进行研究，主要方法有准连续介质力学方法[1]、原子/连续耦合方法[2-3]等；第二类是材料区域，该区域仅包含原子或连续介质，考虑材料的宏观性能与细观结构的关系，代表性方法有均匀化方法，它包括多尺度渐近展开法[4]、收敛估计法[5]、随机处理法[6]等.

对于多孔材料，由于孔洞区域结构复杂，本文考虑使用多尺度渐近展开法求解其特征值问题. 1964年，Marchenko和Khruslylov[4]首次提出多尺度渐近展开法. 随后，Ngnetsent[7]和Allaire[8]提出了双尺度收敛的概念和双尺度收敛分析方法，提供了一种获得均匀化模型的方法. 在此基础上，Cui和Cao[9]通过对二阶展开项的考虑证明了二阶双尺度(Second-Order Two-Scale, SOTS)方法可以有效地预测复合材料的物理力学性能.

此外，使用均匀化方法研究特征值也是一个研究热点.如Kesavan[10-11]提出了周期情况下椭圆型特征值问题的求解方法，Vanninathan[12]研究了周期性孔洞区域的特征值问题，Bonnetier等[13]讨论了Neumann-Poincaré算子的特征值，文献[14]通过坐标变换将一般非周期复合域转换为规则域，并对弹性特征值问题进行了多尺度渐近分析和计算等等.

本文研究了拟周期性孔洞材料模型的椭圆型特征值问题.我们先进行理论分析，然后给出数值算例，验证了二阶双尺度方法在解决曲线坐标下多孔材料模型特征值问题的有效性. 除非特别指出，本文中均使用Einstein求和约定，即重复指标表示求和.

2 特征值问题及坐标变换

为简单起见，我们仅考虑二维问题. 如图1所示，区域Ωε在直角坐标系下是拟周期区域，通过选择适当变换ξ=L(x)，可使得拟周期区域Ωε中的每个点x唯一地映射为周期区域Θε中的点ξ. 于是可以在周期区域Θε中用渐近展开方法对特征值和特征函数进行展开，并在Θε对应的单胞区域Q*上定义单胞函数，得到问题的均匀化解、均匀化系数和多尺度逼近解，最后通过逆变换x=L-1(ξ)得到原问题的解.

图1 坐标变换示意图Fig.1 Coordinate transformation diagram

对于变换后的周期孔洞区域，我们做出如下假设：假设均匀化凸区域Θ为一个有界连通开子集，有Lipschitz边界∂Θ. 定义Θ上孔洞区域为Tε，Θε=Θ-Tε称为孔洞区域. 单胞Q=[0,1]N，单胞Q*=Q-T，其中孔洞T⊂Q为有界开集.称Q*为周期孔洞区域Θε对应的参考单胞.

假设孔洞边界满足Neumann条件，考虑(uε,λε)对应的椭圆型特征值问题为

(1)

α1,α2>0,l=(li)1≤i≤N∈RN.

由偏导数运算

可将原方程改写为

(2)

3 二阶双尺度分析

由二阶双尺度渐进展开方法，我们可以得到(uε,λε)的渐近展开形式

uε(ξ)=u0(ξ,η)+εu1(ξ,η)+ε2u2(ξ,η)+O(ε3),

λε=λ0+ελ1+ε2λ2+O(ε3).

将偏导数运算

以及渐近展开式代入式(2)，比较方程两端ε各幂次系数，得到

(3)

(4)

(5)

其中

根据式(3)可知，u0独立于η.所以

u0(ξ,η)=u0(ξ)

(6)

根据式(6)，可以将式(4)化为

进而可以得到一阶校正项表达式

(7)

Nα1(ξ,η)满足单胞问题

对于式(5)，对等式两端在Q*上做积分平均，结合式(7)，可以得到均匀化解(u0,λ0)对应均匀化方程

(8)

其中均匀化系数

将式(6)～(8)代入式(5)，整理和计算得到二阶校正项表达式

Nα1α2(ξ,η)满足单胞问题

下面考虑特征值的近似解. 基于Kesavan[10]提出的“校正方程”的思想，我们首先令wε(ξ)为以下问题的解：

相应的变分形式为

通过上述连续枯水年的供水风险分析，本论证单元在1999—2002年连续枯水年条件下，可以保证规划水平年2015年、2020年的供水需求。论证区域2015年、2020规划水平年的开采量，分别占多年平均地下水补给量99.3%和98.9%，虽然典型年和连续枯水年须分别动用地下水储存量的3.4%和4.4%，但动用的地下水储存量在丰水年、平水年可以得到回补，因此供水水源可靠。

根据

我们得到校正方程

由二阶双尺度方法，可将wε(ξ)渐近展开为

wε(ξ)=

u0(ξ)+εw1(ξ,η)+ε2w2(ξ,η)+O(ε3).

将uε(ξ),wε(ξ),λε展开式代入校正方程，比较方程两端ε各幂次系数，可以得到

根据均匀化理论[12]，假设uε(ξ),wε(ξ)充分靠近.则

4 有限元计算

其中

当变换为线性变换时，gij全为常数，且J为正，hi=0. 此外，所有单胞函数独立于ξ，于是一、二阶逼近解为

λε,1=λ0+ελ1,λε,2=λε,1+ε2λ2.

这里Nα1(η)满足单胞问题

Nα1α2(η)满足单胞问题

因均匀化解满足

于是各单胞问题以及均匀化问题的变分形式为

∀φ∈H1(Q*;∂Q)，

其中H1(Q*,∂Q)表示空间H1(Q*,∂Q)={φ|φ∈H1(Q*),φ=0 on ∂Q}.

二阶双尺度有限元法的一般计算流程如下:

(1) 设定材料参数，初始化单胞区域网格Q*与均匀化网格Θ，计算函数gijkl,J,hijl.

(3) 利用求得的均匀化解与一阶、二阶单胞函数组装得到一阶和二阶逼近解(uε,1,λε,1),(uε,2,λε,2).

(4) 将特征函数u0,uε,1,uε,2映射到原宏观区域Ωε.

本节最后给出误差分析方法. 首先，引入空间L2(Ωε)中内积与范数

由于任何特征函数乘以一个非零实数也是原问题的特征函数，因而求得的特征函数不能直接进行比较. 为了进行误差分析，我们利用最小二乘思想选择使得两个特征函数在L2范数中误差最小的比例因子，且考虑缩放渐近解.也就是说，选择比例因子使得两个特征函数在L2范数中有最小的误差. 为此，对于单特征值对应的特征函数，我们定义其相对误差为

由此得到比例因子

其中

注意上式中也没有对n求和.

5 数值算例

考虑具有复合结构的孔洞材料，两种材料都是均匀且各向同性的. 通过变换

x1=ξ1+ωξ2,x2=ξ2,

容易得到原宏观区域Ωε、周期区域Θε和单胞区域Q*如图2图3所示.

图2 ε=1/8时原宏观区域Ωε和变换后区域Θε

图3 单胞区域Q*

根据分析得

g11=1+ω2,g12=g21=-ω,g22=1,

J=1,h1=h2=0,

变换后问题变为

假设材料系数为α1=1,α2=0.01，变换系数为ω=0.25. 根据上式，应用有限元方法可得到Nα1(η)，可以计算出均匀化系数

进一步计算可得到Nα1α2(η)，从而得到一阶和二阶逼近解. 最终通过逆变换得到原问题的解. 由于原问题精确解难以求出，这里我们将在原宏观区域细网格下计算得到的解作为精确解与各阶逼近解进行比较.

表1显示了ε=1/8和ε=1/16时的网格信息.随ε减小，原宏观细网格规模增大，网格尺寸减小，原宏观细网格有限元计算量增加. 使用双尺度有限元方法，单胞网格和均匀化网格的单元数与结点数保持不变，计算时间固定.当区域周期ε=1/16时，单胞个数增多，双尺度有限元法更具计算优势.

表1 网格信息

下面首先对特征值进行分析.ε=1/8的前10个特征值和相对误差如表2所示. 从表中看出，均匀化和一阶校正的结果之间相差并不大，与实际结果之间则差距较大.经过二阶校正，所得到的结果明显好于一阶，因而进行二阶校正很有必要.

表2 ε=1/8时前10个特征值和相对误差

下面我们对特征函数进行分析. 图4和图5分别显示了最小特征值(单特征值)和第二个特征值(2重特征值)对应细网格下的特征函数以及各阶逼近特征函数的图像. 从图中容易看出，均匀化特征函数图像光滑且与精确解相差较大，一阶逼近解图像出现局部振荡，但和精确解仍有很大差别，而经过二阶校正，二阶逼近解图像已经和精确解很接近了.

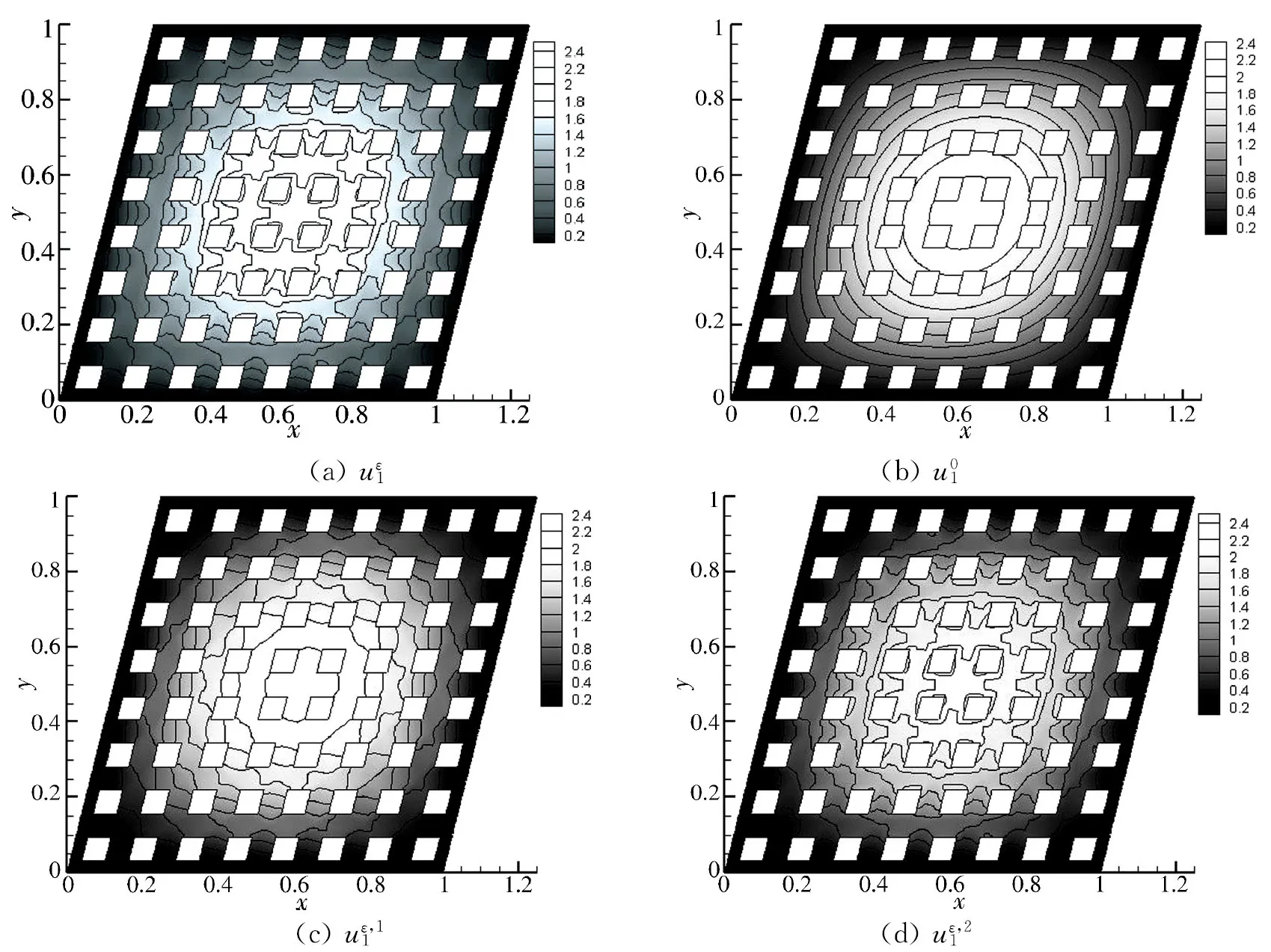
图4 ε=1/8时第一个特征值对应的特征函数

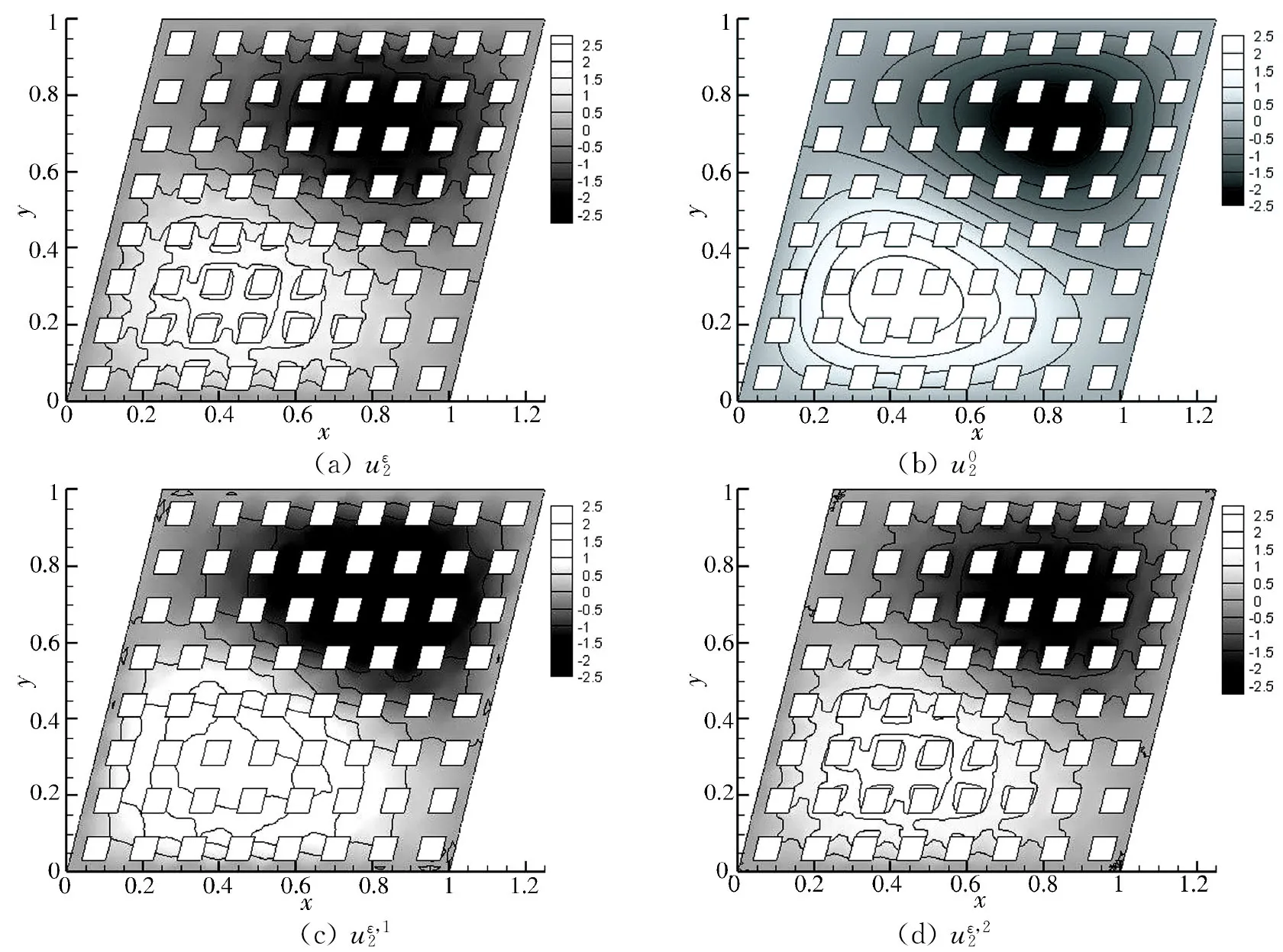
图5 ε=1/8时第二个特征值对应的特征函数

表3给出了L2范数下前10个特征值对应的特征函数的相对误差.能够看出，均匀化结果与精确解误差较大，通过一阶校正能够有效减小误差，但经过一阶校正后仍然不能得到满意的估计结果，二阶校正的精度远远大于一阶. 此外，虽然进行二阶校正能够有效减小误差，但随着n增加特征值增大，所对应特征函数的相对误差也越大.

表3 L2范数下特征函数的相对误差

为考虑特征函数的收敛情况，将ε减小一半，对ε=1/16时的情况进行分析. 图6显示了在不同周期下第10个特征值对应的特征函数图像.容易看出，当ε减小时，精确解和二阶逼近解的特征函数图像更相近. 从计算效果来看，当ε=1/16时，进行相同的有限元计算无论是单特征值或是重特征值所对应的特征函数的相对误差均变小了.

图6 第十个特征值对应的特征函数

6 结论与展望

本文通过坐标变换方法发展了多孔材料结构模型特征值问题的二阶双尺度渐近分析方法，给出了特征函数与特征值的渐近展开表示式，提出了在曲线坐标系下的有限元算法.数值结果验证了二阶双尺度方法解决复杂多孔结构模型特征值问题的有效性.我们的研究表明：

(1) 均匀化解仅反映问题解的宏观性质，有必要借助一阶与二阶校正反映解的局部性质. 但鉴于一阶逼近解远不如二阶逼近解来得精确，为得到更好的结果，必须添加二阶校正项捕捉材料在区域内变化的局部振荡行为，所以将逼近解扩展至二阶是合理且必要的；

(2) 选取适当的ε，对于特征值，二阶校正效果明显优于一阶校正；对于特征函数，经过二阶校正，近似解与精确解已经非常接近；

(3) 双尺度有限元方法所使用的单胞网格与均匀化网格总是相对粗糙的，计算时间固定，当ε越趋近于0时，双尺度有限元方法与传统方法相比更具计算优势；

(4) 数值实验部分考虑了前10个特征值以及单特征值对应的特征函数的相对误差，当特征值越来越大时，使用二阶双尺度有限元方法所得结果的误差也越来越大，因而研究特征值和特征函数的渐近性态，对寻找适当的高阶解的校正具有重要意义.