数字岩心宽频带动态应力应变模拟方法及其对含裂隙致密岩石频散和衰减特征的表征

朱伟， 赵峦啸， 王一戎

1 长江大学油气资源与勘探技术教育部重点实验室， 武汉 430100 2 长江大学地球物理与石油资源学院， 武汉 430100 3 同济大学海洋地质国家重点实验室， 上海 200092 4 同济大学海洋与地球科学学院， 上海 200092

0 引言

非均质性是地下多孔岩石的最基本表征之一.在漫长的地质年代，由于沉积和成岩作用的差异，以及构造运动和地质过程中的随机扰动，岩石往往在各个尺度上表现出不同程度的非均质性.这些非均质性表现为岩石的物质组成、孔隙类型、流体分布、裂隙发育、输运性质等空间分布的不均匀性(Zhao et al.，2020).当弹性波在含流体非均匀孔隙介质中传播时，地层的非均质性不仅影响弹性波的传播速度，而且由于波致孔隙压力差异造成的流体流动还会引起弹性波的频散和衰减效应(Müller et al.，2010).孔隙压力弛豫在不同类型的岩石中造成的弹性波频散和衰减特征已经被大量的实验数据和不同频段的地球物理数据所证实(未睍等，2015；Subramaniyan et al.，2015；Chapman et al.，2019；Ma et al.，2018；Borgomano et al.，2019；李闯等，2020；Li et al.，2020).研究弹性波在不同频段的速度和衰减特征一方面可以指导综合利用多尺度的地球物理数据进行地层非均质性的刻画，另外一方面为利用地震耗散相关的属性进行流体和裂隙储层等预测提供物理基础.同时，这些研究对于非均质储层的地震表征、四维地震的流体监测、二氧化碳封存、地热资源的勘探开发都具有重要的价值(Sams et al.，1997；Zhao et al.，2015；Chen and Innanen，2018;Chen，2020).

近几十年来，很多学者提出大量理论模型来刻画波致流体流动引起的频散和衰减效应(Biot，1962；White，1975；Dvorkin et al.，1995；Gurevich et al.，1997；Chapman et al.，2002；Pride et al.，2004；Ba et al.，2008, 2017；Tang，2011；巴晶等，2012；Yao et al.，2015；Zhao et al.，2017；Papageorgiou and Chapman，2017；Jin et al.，2018；赵正阳等，2019)，这些理论大多基于对岩石非均质特征(比如孔隙结构或者分布形式)的一些简化和假设，聚焦于探讨不同的地质和物理参数对频散和衰减特征的影响.相对而言，数字岩石物理技术则可以很好地弥补这种不足，可以模拟各种接近实际复杂非均质多孔岩石的孔隙结构、裂隙形态、流体分布，从而可以全面准确刻画复杂非均质多孔岩石中波致流体流动引起的频散和衰减效应.这些数字岩心的尺度虽然比实际地层要小很多，但其揭示的基本物理过程和规律却对综合利用多频段地球物理数据进行多尺度地质特征刻画有重要的启示意义.

数字岩心是数字岩石物理的模型基础，可以用数学重建方法或物理实验方法建立.在一定空间尺度上，数学重建方法建立的数字岩心与真实岩心的孔隙结构具有统计相似性，物理实验方法建立的数字岩心与真实岩心的孔隙结构十分接近(朱伟和单蕊，2014).在数字岩心中，固体骨架和孔隙流体是相互独立的介质，通过边界连接在一起.质点的介质类型是固体和流体中的一种，而不是多相孔隙介质模型中固体和流体共存的情况.数字岩石物理中的弹性/黏弹性模拟技术主要包括四种：1)静力学模拟(Arns et al.，2002；Zhang et al.，2016)；2)透射波模拟(Saenger and Shapiro，2002；Saenger et al.，2011；印兴耀等，2016；Li et al.，2019)；3)准静态应力应变模拟(Quintal et al.，2016，2019；Alkhimenkov et al.，2020a，2020b；Lissa et al.，2020)；4)动态应力应变模拟(Zhang and Toksöz，2012；Zhu et al.，2017；Das et al.，2019；朱伟等，2020).Zhang和Toksöz(2012)首次提出了数字岩心动态应力应变模拟方法，计算了砂岩数字岩心在频率为100 kHz时的速度和衰减.Zhu等(2017)建立了一种沿不同方向计算数字岩心的速度和衰减的动态应力应变模拟方法.Das等(2019)利用动态应力应变模拟技术分析频散和裂隙扁率、频散与流体黏滞系数的关系.朱伟等(2020)利用动态应力应变模拟方法研究砂岩CT数字岩心内部的位移场和孔隙压力的空间和时间变化.

现有的数字岩心动态应力应变模拟为单频率模拟方法，通过使数字岩心发生简谐型应变计算某一频率的速度和衰减.单频率模拟可以提取任意模拟时刻数字岩心的流体位移和孔压变化，并与速度、衰减进行关联分析，但须在不同频率进行多次模拟才能得到频散和衰减曲线的基本形态.为了不漏掉重要的细节特征，模拟频率必须仔细选择，增加了数值模拟的复杂性.

因而，为了较为全面准确刻画非均质多孔岩石在全频段(地震—超声)的频散和衰减特征，需要发展相应的数字岩心模拟技术.宽频带动态应力应变模拟期望给数字岩心加载一个恒定应变，模拟数字岩心内部应力松弛过程，通过一次模拟计算一个频带内的频散和衰减曲线.对地震岩石物理学而言，宽频带的频率范围是零至某个最大频率，模拟时只需考虑最高截止频率即可.在宽频带模拟中也可以提取任意时刻的流体位移和孔压变化，但不能与某个频率简单联系起来.

裂隙在多孔岩石尤其是致密地层中普遍存在.虽然裂隙在岩石中只占很小的体积百分比，但对岩石的弹性和渗透性有极大的影响.在一些致密储层中，从地震上找到裂隙发育区的“甜点”成为致密储层开发的关键，理解含裂隙致密岩石的地震弹性和衰减特征是裂隙属性地震评价的基础.当地震波通过含裂隙的致密岩石时，裂隙由于可压缩性要大于背景孔隙(如粒间孔、溶蚀孔洞等)，因而会引起地质流体在裂隙和背景孔隙之间交流，并引起弹性波的频散和衰减，一般被称为挤喷流效应.

本文首先详细介绍宽频带动态应力应变模拟的原理；然后将该方法用于刻画含裂隙致密岩石挤喷流效应引起的速度频散和衰减特征，并通过数字岩心模拟较为系统的揭示了致密地层中控制挤喷流效应的主控物理因素，也证明了该方法在表征复杂非均质多孔岩石波致流体流动引起的频散和衰减特征的适用性.

1 基本原理

1.1 边界条件

当前地震勘探仍以纵波勘探为主，对数字岩心设置如图1所示的边界条件，可计算纵波沿x轴方向传播时的频散和衰减.在数字岩心的上、下边界应用周期性边界条件，相当于将数字岩心的上、下两个边界连接在一起，即如果波从上边界出射，则波将从下边界上相同的水平位置以相同的方向入射，反之亦然.由于数字岩心在垂直方向受限，这使计算水平方向的纵波传播性质变得容易.

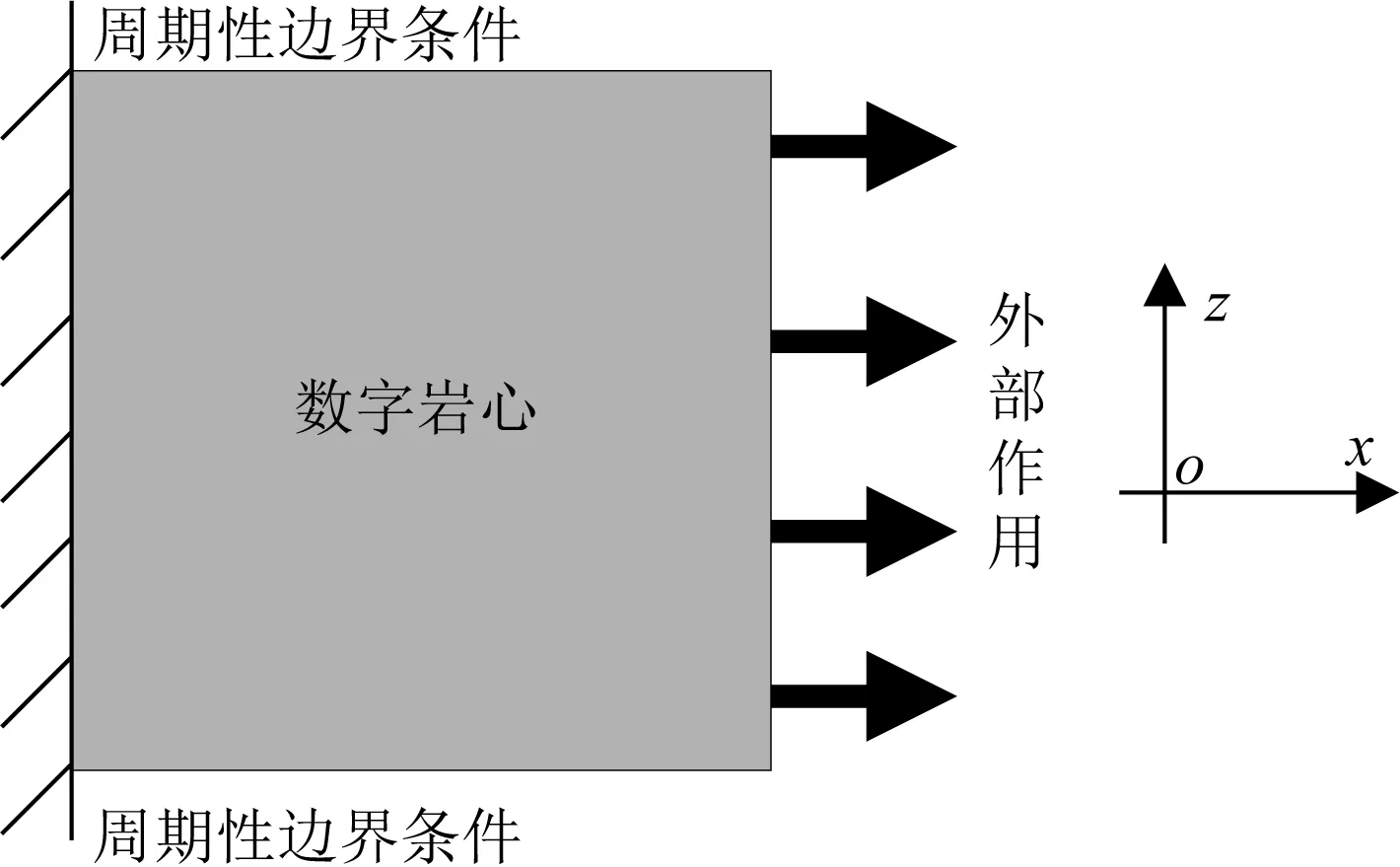
图1 数字岩心的边界条件示意图Fig.1 Setup of boundary condition on digital rock

数字岩心的左边界静止不动，右边界受到外部动态作用，数字岩心发生水平方向的受迫运动.在t=0时刻，数字岩心中质点的速度和位移均为零，即

vx(x,z,t=0)=0,

vz(x,z,t=0)=0,ux(x,z,t=0)=0,

uz(x,z,t=0)=0.

(1)

式中，vx和vz是质点在x和z方向的速度分量，ux和uz是质点在x和z方向的位移分量.

当t≥0时，数字岩心左边界质点的速度分量为

vx(0,z,t)=0,

vz(0,z,t)=0.

(2)

当t≥0时，数字岩心右边界质点的速度分量为

vx(L,z,t)=A·f(t),

vz(L,z,t)=0.

(3)

式中，L表示数字岩心的边长；f(t)是t的函数，f(0)=0；A是调节应变大小的常数，使数字岩心在x方向满足小应变假设.

函数f(t)的形态是宽频带模拟和单频率模拟的核心区别.在单频率模拟(Zhu et al.，2017)中，f(t)是某个频率的正弦函数.在宽频带模拟中，f(t)相当于一个低通信号，在通带内振幅近似为常数，在压制带内振幅近似为零，模拟得到通带内的频散和衰减曲线.函数f(t)的一个可能实现如图2a所示，类似于一个延迟尖脉冲函数，它表示数字岩心右边界质点的速度分量vx随时间的变化，而右边界质点的位移分量ux随时间的变化可以用图2b表示.质点的位移是速度的时间积分，因此对图2a中的曲线进行时间积分就得到图2b中的曲线(图2中曲线幅度为归一化值).当模拟时间增大时，数字岩心右边界质点的位移分量ux趋于某一稳定值.因此，在右边界上的外力作用下，数字岩心的宏观应变逐渐趋于定值，而数字岩心内部的应力场逐渐平均化，发生应力松弛.图2c是f(t)的振幅谱，具有低通性质，在通带内振幅值基本稳定.若f(t)越接近尖脉冲函数，则其通带越宽.

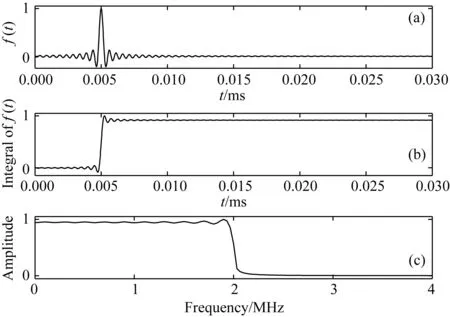
图2 归一化的f(t)、f(t)的积分和f(t)的振幅谱(a) 函数f(t)； (b) f(t)的积分; (c) f(t)的振幅谱.Fig.2 Normalized f(t), integral of f(t) and amplitude spectrum of f(t)(a) The function f(t); (b) The integral of f(t); (c) The amplitude spectrum of f(t).

1.2 波场模拟

假设数字岩心的骨架由各向同性的线弹性介质组成，其本构方程为

(4)

式中，λ和μ是拉梅常数；σxx，σzz和σzx表示应力；exx，ezz和ezx表示应变.

假设数字岩心饱和牛顿流体，牛顿流体的本构关系为

(5)

式中，ηλ和ημ表示黏滞系数，在模拟中令ηλ=ημ=η.

用位移和应力表示的运动方程为

(6)

式中，ρ表示密度.

求解方程组(4)、(5)和(6)的方法是旋转交错网格有限差分法(Saenger et al.，2000).图3表示旋转交错网格的网格设置，位移和速度分量位于网格顶点，应变、应力、弹性模量、黏滞系数和密度定义在网格中心.

图3 旋转交错网格示意图Fig.3 Sketch map of rotated staggered grid

若采用2阶精度的旋转交错网格有限差分格式，则速度和位移的有限差分可直接用下面的公式表示.

(7)

式中，ψi可表示网格顶点的位移和速度，下标i=1,2,3,4表示网格的4个顶点的标号.

公式(7)可视为两个中心差分格式的平均，用网格的4个顶点的速度和位移计算它们在网格中心的有限差分值.应变和应变率分别是位移和速度的空间导数.故应变、应变率、弹性模量和黏滞系数都定义在网格中心，更新应力时不需要对弹性模量和黏滞系数插值，流固边界附近的应力稳定.当更新网格顶点的速度和位移时，需要使用以该顶点为公共顶点的4个网格来计算应力的有限差分.由于密度定义在网格中心，网格顶点的密度需要由周围4个网格的密度进行平均.密度插值对迭代算法是稳定的.因此，在旋转交错网格有限差分中不需要对流固边界做特别处理.

1.3 纵波的速度与逆品质因子

在模拟过程中计算数字岩心的平均正应变和正应力，在模拟结束后计算应变率和应力率.数字岩心的复纵波模量是应力率和应变率的傅立叶变换的比值.数字岩心的纵波速度和逆品质因子由复纵波模量和密度计算.上述过程可以用公式(8)表示.

(8)

1.4 精度验证

本文采用均匀牛顿流体模型验证模拟方法的精度.牛顿流体的体积模量为2.3 GPa， 黏滞系数为1.0 Pa·s，密度为1000 kg·m-3.模型网格的长度为1.0×10-6m，模拟时间步长为1.0×10-10s，模拟时间长度为1.0×10-3s.数值模拟计算的频散和逆品质因子如图4a和图4c所示.由公式(5)可知，牛顿流体的复纵波模量为M(ω)=λ+i3ωη，可利用公式(8)的后三式计算频散和逆品质因子的解析解，显示于图4a和图4c中.

由图4可知，1)频散和逆品质因子的数值解与解析解基本重合，误差非常小(图4b和图4d)；2)对于均匀牛顿流体而言，速度和逆品质因子随频率单调增加，但在图4的频率范围内频散和衰减程度均很小.

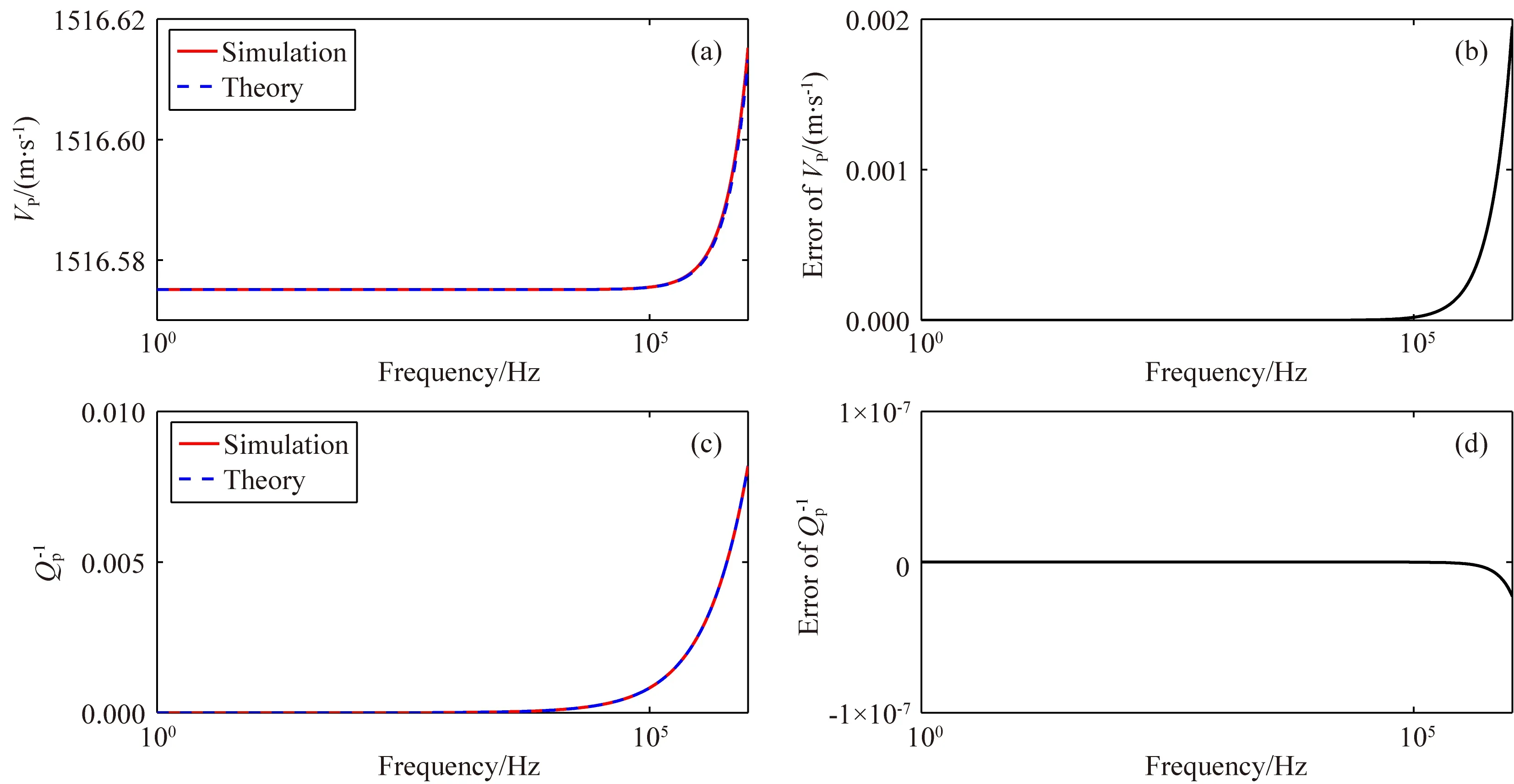
图4 牛顿流体的频散和逆品质因子(a) 速度频散曲线； (b) 速度的数值解与解析解之差； (c) 逆品质因子曲线； (d) 逆品质因子的数值解与解析解之差.Fig.4 Velocity dispersion and inverse quality factor of Newtonian fluid(a) Velocity dispersion curve; (b) Velocity difference between simulation and theory; (c) Inverse quality factor curve; (d) Inverse quality factor difference between simulation and theory.

2 含裂隙致密岩石的频散和衰减特征数值模拟

这一部分将数字岩心宽频带动态应力应变模拟方法用于表征含裂隙致密岩石的挤喷流效应，一方面旨在细究控制含裂隙致密地层挤喷流效应的主控物理因素，另一方面也证明该方法在刻画复杂非均质多孔岩石由于波致流体流动引起的速度频散和衰减特征的有效性.当岩石受到挤压或拉伸时，裂隙中的流体压力变化较大，在孔隙中形成较大的压力梯度，驱动孔隙压力在“较软”的裂隙和较硬的孔隙之间扩散，导致波的频散和衰减.针对含裂隙致密岩石的物理特征，本节建立了4个二维数字岩心，用宽频带动态应力应变数值模拟方法计算数字岩心的频散和逆品质因子曲线，并分析其特征.

2.1 数字岩心构建

为了刻画挤喷流效应，数字岩心包含若干相互独立的裂隙—圆孔系统.裂隙为直裂隙，走向垂直外部挤压(拉伸)方向，一端与圆孔相连，另一端封闭，见图5.数字岩心a和b的边长为1.0×10-3m，孔隙度分别约为0.020和0.051.裂隙的长度为8.8×10-5m，宽度为3×10-6m，扁率(也称纵横比，定义为矩形裂隙的宽度与长度的比值)约为0.034，圆孔半径为1.5×10-5m.数字岩心c和d的宽度为0.5×10-3m，高度为1.0×10-3m，孔隙度分别约为0.024和0.052.裂隙的长度为8.8×10-5m，宽度为1.5×10-6m，扁率约为0.017，圆孔半径为1.5×10-5m.

这里采用硬币状裂隙的近似公式Cr=3φc/4πα计算裂隙密度，φc为裂隙孔隙度，α为裂隙扁率(Hudson，1981；Mavko et al.，2009).数字岩心a、b、c和d的裂隙密度分别约为0.035，0.089，0.048和0.104.

图5 数字岩心数字岩心a和b的边长为1.0×10-3 m，孔隙度分别为0.020和0.051.裂隙长度约8.8×10-5 m，裂隙宽度约3×10-6 m，扁率约0.034，圆孔半径约为1.5×10-5 m.数字岩心c和d的宽度为0.5×10-3 m，高度为1.0×10-3 m，孔隙度分别为0.024和0.052.裂隙长度约8.8×10-5 m，裂隙宽度约1.5×10-6 m，扁率约为0.017，圆孔半径约为1.5×10-5m.Fig.5 Digital rocks Side length of digital rock a and b is 1.0×10-3 m, their porosity are 0.02 and 0.051. The length and width of cracks are 8.8×10-5 m and 3×10-6 m, the aspect ratio is 0.034. Radius of pores is 1.5×10-5 m. The width and height of digital rock c and d are 0.5×10-3 m and 1.0×10-3 m, their porosity are 0.024 and 0.052. The length and width of cracks are 8.8×10-5 m and 1.5×10-6 m, the aspect ratio is 0.017, Radius of pores is 1.5×10-5 m.

这4个数字岩心的骨架由同一固体介质构成，孔隙被同一流体饱和.固体与流体的参数见表1.综合考虑模拟效果、裂隙扁率、模型大小和计算负担，我们对流体设计了较大的黏滞系数(朱伟等，2020).

表1 数字岩心骨架固体和孔隙流体的黏弹性参数表Table 1 Viscoelasticity of solid matrix and pore fluid in digital rock

数值模拟采用基于正方形网格的有限差分法，在对数字岩心离散化后，孔隙和骨架的界面局部呈现锯齿状，这可能会影响波致流体流动.但是，数字岩心的裂隙为直裂隙，裂隙面与网格边界走向一致，离散后的裂隙表面仍然是光滑的，不存在锯齿状的情况.当数字岩心受到垂直裂隙面方向的挤压(拉伸)时，强烈的流体运动发生在裂隙中.所以，裂隙中的挤喷流基本不受锯齿状孔隙边界的影响.

2.2 模拟测试

当裂隙饱和黏性流体时，需要对裂隙宽度进行充分采样以便以适当的精度刻画波致流效应.我们以数字岩心b为例进行网格剖分和数值模拟试验，确定离散裂隙宽度所需的网格数量.首先，将裂隙宽度离散为3个网格；然后，以此为基础，逐步加密网格(即减小网格大小)，分别得到裂隙宽度为6个和12个网格的模型.如此，我们得到3个离散的数字岩心网格模型，它们的大小和结构完全相同，只是网格大小和数量不同.裂隙宽度分别为3个、6个和12个网格.

在数值模拟中，3个模型采用相同的模拟时间步长和总时长，得到的频散和逆品质因子曲线如图6所示.函数f(t)的通带范围为0～2 MHz，当频率高于1 MHz后，由于波场散射逐渐明显，平均应力曲线中包含了较多扰动，频散和逆品质因子曲线的高频干扰比较严重，故在图6中频率上限为1 MHz.

由图6可知，这3个模型的频散和逆品质因子曲线的形态基本一致，但特征频率发生变化.当裂隙宽度为12个和6个网格时，特征频率非常接近.当裂隙宽度为3个网格时，特征频率向低频方向略有移动.

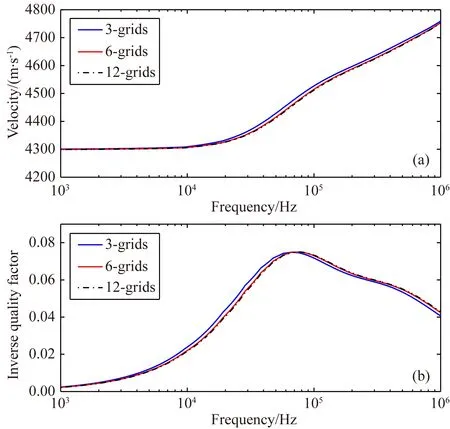
图6 数字岩心b的频散和逆品质因子曲线曲线3-grids、6-grids和12-grids分别对应裂隙宽度用3个、6个和12个网格离散.Fig.6 Dispersion and attenuation of digital rock b Curves named with 3-grids, 6-grids and 12-grids corresponding to crack width sampled by 3, 6 and 12 grids, respectively.

离散模型的网格越小，模拟结果的精度越高，这是数值模拟的一个基本特征.但是，网格减小会使网格数量增加、模拟步长减小，从而大幅提高计算工作量.因此，在精度合理的前提下，网格大一点对完成数值模拟有利.在本文中，我们认为用6个网格对裂隙宽度进行离散比较合适.进一步加密网格可以提高精度，但效果逐渐不明显.

与网格大小有关的另一不利影响因素是数值频散.但当波长与网格边长的比值较大时，数值频散可以勿略.当数字岩心的裂隙宽度分别为3个，6个和12个网格时，网格边长分别为1.0×10-6m，0.5×10-6m和0.25×10-6m.弹性波在骨架矿物和孔隙流体中的纵、横波速度分别约为6008 m·s-1，4075 m·s-1和1517 m·s-1.以最高频率1 MHz计算的最短波长约为1.517×10-3m.波长与网格边长的最小比值约为1517，即最短波长远远大于最大网格边长，在此条件下数值频散非常小，不影响挤喷流的频散效应.

2.3 模拟结果

根据2.2小节的试验结果，我们采用6个网格对裂隙宽度进行离散.相应地，数字岩心a和b的网格大小为0.5×10-6m，数字岩心c和d的网格大小为0.25×10-6m.两组数字岩心的模拟时间步长分别为0.25×10-10s(a和b)和0.1×10-10s(c和d).数字岩心c和d的裂隙扁率比数字岩心a和b小.根据挤喷流理论推测数字岩心c和d中流体压力平衡过程需要更长的时间.两组数字岩心的模拟时间长度分别为1.25×10-4s(a和b)和5.0×10-4s(c和d).

图7为上述4个数字岩心的模拟结果，图7a和图7b分别为频散和逆品质因子.在图7a、图7b中，曲线a，b，c和d分别表示数字岩心a，b，c和d的模拟结果.

图7 数字岩心的模拟结果(a) 速度; (b) 逆品质因子.曲线a、b、c、d分别表示数字岩心a、b、c、d的模拟结果，φa，φb，φc和φd表示总孔隙度，Cra，Crb，Crc和Crd表示裂隙密度.Fig.7 Simulation results of digital rocks(a) Velocity; (b) Inverse quality factor. Curve-a, -b, -c and -d are results of digital rock-a, -b, -c and -d respectively.φa,φb,φc and φd represent total porosity.Cra, Crb, Crc and Crd represent crack density.

频散曲线表现的特征为：数字岩心a和c的速度明显要比数字岩心b和d高，这主要是由于数字岩心b和d的裂隙密度较高造成的.裂隙是一种体积和扁率非常小，但对岩石弹性影响非常大的孔隙类型.这4个数字岩心中的裂隙是定向排列的，垂直裂隙面方向的波速受到裂隙的影响最大.当频率小于103Hz时，数字岩心a与c的速度基本不随频率变化，这主要是由于在此频段内，裂隙内流体近似处于松弛状态；而数字岩心c比a的速度稍低，这主要还是由于数字岩心c的孔隙度比a稍高，所以数字岩心c在松弛阶段的速度稍低.相较与数字岩心a，数字岩心c开始出现明显频散效应的频率较低，这主要是由于数字岩心c的裂隙扁率较小，因此特征频率较低.这符合一般的物理认识，也就是扁而长的裂隙往往需要更长的时间进行孔隙压力弛豫，因此其衰减的特征频率也会较低.而且由于频散效应，数字岩心c的纵波速度很快超过了数字岩心a，这主要是因为数字岩心c稍高的裂隙密度造成的，这样有更多的流体在较软的裂隙和较硬的圆孔之间交流，引起了较大的频散效应.类似于数字岩心c和a，数字岩心d的频散效应明显高于数字岩心b，并且特征频率出现在较低的频段.在低频段数字岩心d的速度稍稍高于数字岩心b的速度，但数字岩心d的孔隙度却略高于数字岩心b.这可以用孔隙结构的变化来解释.

如图7b所示，数字岩心的衰减特征与速度频散有较好的对应关系.可以清楚地看到，数字岩心b与a、数字岩心d与c分别具有近似一样的特征频率，这也证明了在其他物理参数一样的情况下，裂隙扁率对特征频率的控制作用.而数字岩心b和d的衰减幅度明显要高于数字岩心a和c，这也一定程度上反映了裂隙密度对衰减幅度的一阶控制作用.另外，在特征频率的低频侧，逆品质因子下降速率较快；而在特征频率的高频侧，逆品质因子下降速率较慢，而且下降速率变化，下降速率快、慢交替出现.这个现象在图7b(因为纵轴为逆品质因子的对数)中不易发现，但在图6中比较明显.

3 讨论

3.1 单频率与宽频带动态应力应变模拟的关系

单频率模拟计算某一频率的速度和逆品质因子，可提取任意模拟时刻孔隙流体压力变化的快照进行分析.宽频带模拟可以计算一个频带范围内的频散和逆品质因子曲线.两者联合分析的基础是它们的结果具有较好的一致性.图8展示了数字岩心a和b的单频率和宽频带动态模拟结果的对比图，其中单频率模拟的频率为50 kHz、65 kHz和75 kHz.可以清楚地看到，在这三个频率处，两种方法的结果几乎一致，说明两种方法的一致性较好.

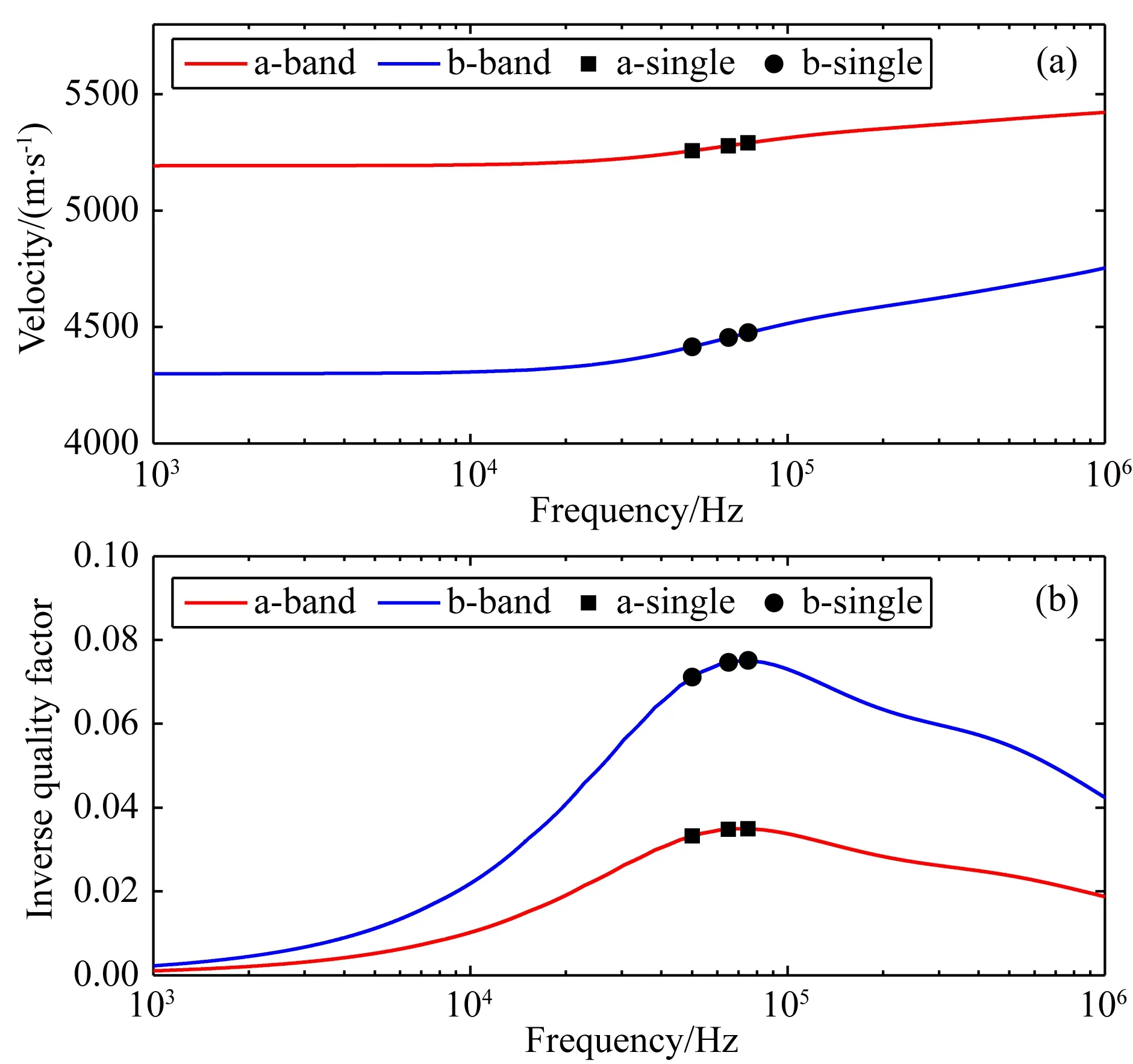
图8 单频率和宽频带模拟结果比较(a) 速度; (b) 逆品质因子.数字岩心为a和b，单频率模拟的频率为50 kHz、65 kHz和75 kHz.图例中a-band和b-band表示数字岩心a和b的宽频带模拟结果，a-single和b-single表示数字a和b的单频率模拟结果.Fig.8 Comparison of the results of single-frequency and broadband simulation (a) Velocity; (b) Inverse quality factor. The models are digital rock-a and -b, frequencies of the single-frequency simulation are 50 kHz, 65 kHz and 75 kHz. In legend, a-band and b-band represent the broadband simulation results of digital rock-a and -b, a-single and b-single represent the single-frequency simulation results of digital rock-a and -b.

3.2 含裂隙致密岩石的频散和衰减特征的控制因素分析

含裂隙致密岩石的特征频率与裂隙扁率的关系符合挤喷流模型的基本特征，即裂隙的扁率减小，则其对应的特征频率向低频方向移动.喷流模型的特征频率(Saenger et al.，2011)为

(9)

式中，Km为基质体积模量，α为裂隙扁率，η为流体的黏滞系数.若特征频率的变化仅由裂隙扁率引起，那么裂隙扁率分别为0.034和0.017的两组数字岩心的特征频率的比值为8.实际两组数字岩心的特征频率的平均比值约为7.数字岩心模拟的特征频率比值与挤喷流理论模型计算的比值接近，验证了裂隙扁率是挤喷流频散效应特征频率的主控因素，而两者差异可能与裂隙-圆孔系统的物理描述、空间分布及其弹性相互作用都有关系.

图9 衰减峰值与裂隙密度的关系Fig.9 Relationship between peak of inverse quality factor and crack density

图9显示了10个数字岩心(含数字岩心a、b、c和d)的逆品质因子的峰值与裂隙密度的关系.折线相连的实心圆表示5个裂隙扁率为0.017的数字岩心.折线相连的正方形表示5个裂隙扁率为0.034的数字岩心.由图9可知，在图示的裂隙密度范围内，当裂隙扁率相同时，衰减峰值与裂隙密度总体上具有近似线性的正相关性，这与一些挤喷流理论模型的结论相似(Tang，2011；Yan et al.，2014)，但也受到孔隙结构的影响而产生局部变化.不同的裂隙扁率对衰减幅度-裂隙密度的关系有显著的影响.裂隙密度相近条件下，狭长的裂隙(扁率较小)引起的衰减幅度更高.

从图7可知，逆品质因子在低于特征频率的一侧随着频率的减小下降较快，而在高于特征频率的一侧随着频率的增加下降较慢，这应该主要是由于挤喷流效应造成的(Gurevich et al.，2010；Alkhimenkov et al.，2020a).另外，考虑到即使频率为1 MHz时，波长与裂隙-圆孔系统总长度的比值可达40，根据频散程度与波长-散射体尺度比值的关系，此时弹性散射引起的频散和衰减程度是比较小的(Mavko et al.，2009).所以，本文动态应力应变数值模拟的结果基本上是挤喷流效应的反映.弹性散射对频散和衰减的作用可能在更高的频带呈现，但前提是需要对平均应力曲线进行适当的压噪处理.

3.3 对缝洞型储层地震勘探的启示

本例中频散和衰减主要发生在声波—超声波频带内，也就是说对于含微观尺度裂隙的岩石来说(<1 cm)，微裂隙与基质孔之间的挤喷流效应对测井数据的影响可能是显著的.由于考虑到计算成本的问题，数字岩心的尺度较小，但所研究的模型对于大尺度的裂隙储层来说也具有重要的启示意义.比如塔里木盆地深层碳酸盐岩储层断裂-溶蚀系统非常发育，因此中大尺度的裂隙往往与溶蚀洞构成复杂的储集空间.而正如本研究所揭示的那样，当地震波通过该类储层时，中大尺度的裂隙与溶蚀洞之间同样可以发生孔隙压力的弛豫或者流体的交换，因此一样会引起地震频散和衰减.这里的数值模拟表明裂隙与孔洞间的流体交换所致的频散和衰减的特征频率与裂隙的扁率密切相关.也就是裂隙的张开度与裂隙长度的比值足够低时，其特征频率很可能发生在勘探地震的主频内，从而对利用地震数据进行深层断溶储层的刻画有重要启示意义.

4 结论

为了刻画复杂非均质多孔岩石在跨频段(勘探地震、声波测井、超声波)的频散和衰减特征，本文提出了基于数字岩心的宽频带动态应力应变模拟方法.该方法以固液耦合的波动方程为基础，模拟数字岩心的应力松弛过程，计算数字岩心在目标频带范围内的频散和衰减特征.通过将该方法成功用于表征含裂隙致密岩石的挤喷流效应，证明了该方法可以用于有效刻画复杂非均质多孔岩石波致流体流动引起的频散和衰减特征.含裂隙-圆孔系统的数字岩心的宽频带动态应力应变数值模拟结果显示，裂隙的扁率对速度频散和衰减的特征频率有很强的控制作用，较小的裂隙扁率对应着特征频率向低频移动；频散和衰减的强度则与裂隙密度和裂隙扁率都有关系，较高的裂隙密度和较小的裂隙扁率对应着较强的衰减幅度.