协同度测度模型在充填方式优选中的应用
2021-06-02王玉珏周英烈
宾 峰 王玉珏 周英烈 周 鑫 朱 敏
(1.飞翼股份有限公司;2.湖南省矿山充填装备工程技术研究中心;3.湖南宝山有色金属矿业有限责任公司)
充填系统是一个涉及经济、技术、安全、资源等多因素的复合系统,充填方式的选择必然是一个涉及多层次、多因素、多目标、多指标的系统决策过程[1]。目前测度系统协同度的方法主要有灰关联熵法、全面协同度模型、基于序参量的复合系统协同度测量模型[2]等。基于序参量的系统协同度模型不仅能测度子系统协同度,而且能通过测度子系统的有序度动态反映系统的变化趋势,这与协同学理论认为复杂系统由许多子系统构成,子系统内部运行规律决定复合系统演化特征内涵相一致[3-6],因此,本研究选择基于序参量的系统协同度模型测度充填系统协同度,对充填方式进行优选。
1 基于序参量的充填系统协同度测度模型
1.1 有序度模型

从上述定义式(1)中可知,μj(eji)∈[ 0,1 ],显然子系统的有序度越大,则意味着eji对该子系统有序度的影响越显著,但是并不意味着eji的取值越大越好,而是集中在某一特定的点周围为最合适。必要时,可通过改变区间[βji,αji]的取值,使其满足式(1)的定义。
定义2[2]一子系统的有序程度取决于该子系统中所有有序参量分量对其的作用。不妨以有序参量ej作为衡量子系统Sj有序度的1 个指标参数,各个分量对子系统的影响不仅表现于分量取值的大小,还体现在各分量对子系统的作用形式。在工程应用中,对于子系统的有序度一般采用式(2)或(3)计算。
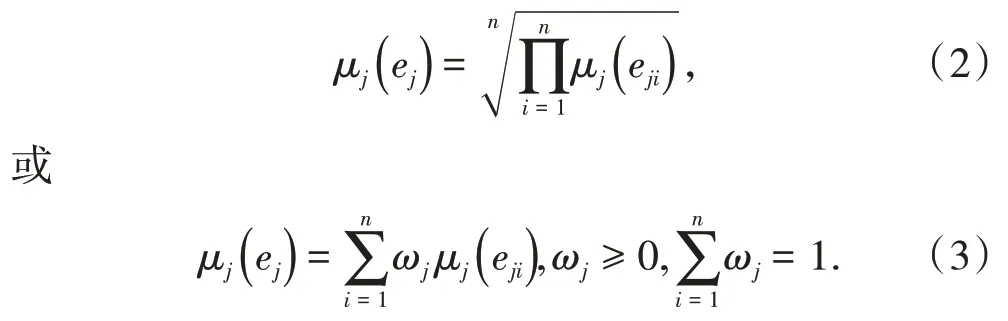
从上述定义式中可知,μj(ej)∈[ 0,1 ],μj(ej)随ej的改变成递增变化。这说明子系统中有序参量的分量值越大,则对该子系统的有序度增幅越明显,反之越低。对于式(3)来说,ωj的取值不仅仅要考虑子系统单独的状态,还需体现该子系统与整个系统之间的关联。
1.2 协同度模型
定义3[2]系统协同度测度模型指定需要研究的某段时间内充填系统有序度的起始时刻为t0,该时刻所对应的充填方式子系统有序值为,j∈[ 1,m],并设研究时段内起始时刻t0后的某时刻为t1,该时刻充填方式子系统有序值为,j∈[ 1,m],定义式(4)为充填系统协同度测度模型(Synergy of Mining System),简称SMS模型。
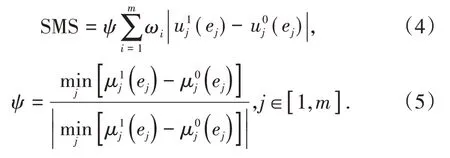
对上述定义3做如下说明。
(1)分析式(4)的数学意义可知,SMES ∈[ -1,1 ],其值越大,则矿山开采系统协性越高,反之则越低。
(2)参数ψ的意义在于,当且仅当对于成立,充填系统才有正的协同度。
(3)该模型排除了部分子系统有序度取值增加甚至出现小幅波动的情形。该情形下,系统处于非良好协同状态,主要体现为SMES ∈[ -1,0 ]。
(4)该定义的主要作用在于可通过部分估计整体发展过程,即可运用子系统的有序度值变化评价整个系统的协同度,并进一步预测整个系统发展状态。
2 充填系统协同度测度实例
以湖南某金属矿山为例,该矿山目前主要采用上向水平分层充填法,主要充填方式为废石非胶结充填,随着开采水下往深部延伸,开采技术条件复杂,顶底板稳固性变化大,在顶板围岩或者矿体不稳定区段,干式充填无法满足深部矿体开采需求,为控制地压活动,提高资源回采率,确保作业安全,需要重新建立完善的充填系统,提出全尾砂废石胶结充填、全尾砂膏体充填、移动式泵送充填3种充填方式,考虑充填系统是一个复杂的系统,为比较上述充填方式的优劣点,本研究采用协同度测度模型从经济、技术、安全、资源等多指标进行充填方式的比较与优选。
2.1 协同度测度模型原始数据
2.1.1 子系统序参量的确定
技术、经济、资源、安全各子系统序参量的确定,选取充填料产出量、输送难易程度、工艺复杂程度、充填速度、接顶难易程度作为技术子系统的序参量[7],选取初期投资成本、运营费用作为经济子系统的序参量,选择充填体强度、充填体沉降速度作为安全子系统的序参量,选择贫化率、损失率作为资源子系统的序参量,各序参量原始数据见表1。其中部分序参量的原始数据取值原则如下。
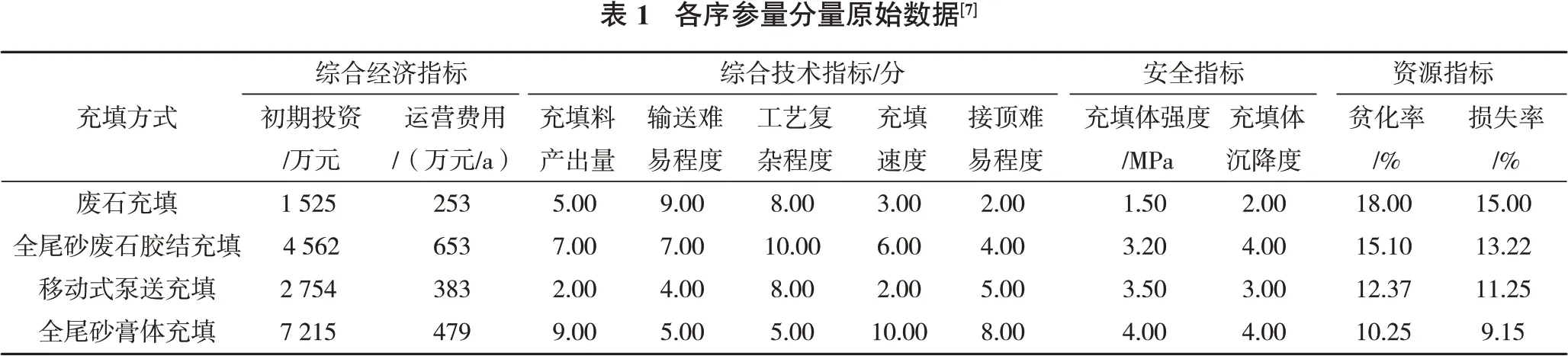
(1)投资总费用。查阅相关资料,参考类似系统投资概算。
(2)充填运营费用。包括设备维修、零部件更换、人工劳务成本、充填材料消耗等,参考类似规模的同类型充填系统。
(3)充填料产出能力。考虑充填物料来源、充填料需量等因素,约定分别为极充足、充足、一般、不充足、极不充足等5个等级,采用定性指标进行判断,各指标依次对应10 分、8 分、6 分、4 分、2 分。
(4)充填工艺复杂程度。根据工程经验,依据不同充填方式各环节间的衔接度、自动化程度等划分为5个等级:极复杂、复杂、一般、简单和极简单,采用定性指标进行判断,各指标依次对应10 分、8 分、6分、4分、2分。
(5)充填料输送难易度。考虑料浆的物料性质、输送浓度、充填距离、输送倍线等因素,约定为SSS、SS、S、A 和B 等5 个等级,同样采用定性指标进行判断,各指标依次对应10 分、8分、6分、4分、2分。
(6)充填速度。根据相关资料和经验以及专家意见确定。
(7)充填结顶难度。考虑不同充填方式下物料的流动性能、离析程度等因素,约定为极易、较易、一般、较难、极难等5 个等级,依次对应10 分、8 分、6分、4 分、2 分。
(8)充填体强度。查阅相关资料,根据类似的实验结果确定。
(9)充填体沉降度。沉降速度跟泌水程度等因素有关,约定很大、较大、一般、较小和极小5个等级,为了易于比较和计算,将该指标确定为定性指标,依次对应10分、8分、6分、4分、2分。
(10)贫化率、损失率。查阅相关资料,参考类似矿山确定。
2.1.2 数据标准化处理
由于各序参量量纲的不同,首先利用SPSS1 9.0对序参量的原始数据进行标准差法(Z-Score)无量纲化处理,以消除量纲不同带来的干扰。结果见表2。

2.1.3 各序参量指标权重的确定
对于矿山开采系统而言,不仅要求技术先进、经济合理,同时要求资源利用率高,主要考虑资源、技术、经济、安全4 个子系统之间的协同程度,本研究采用熵值法确定各序参量权重,见表3。

2.1.4 子系统序参量的功效值计算
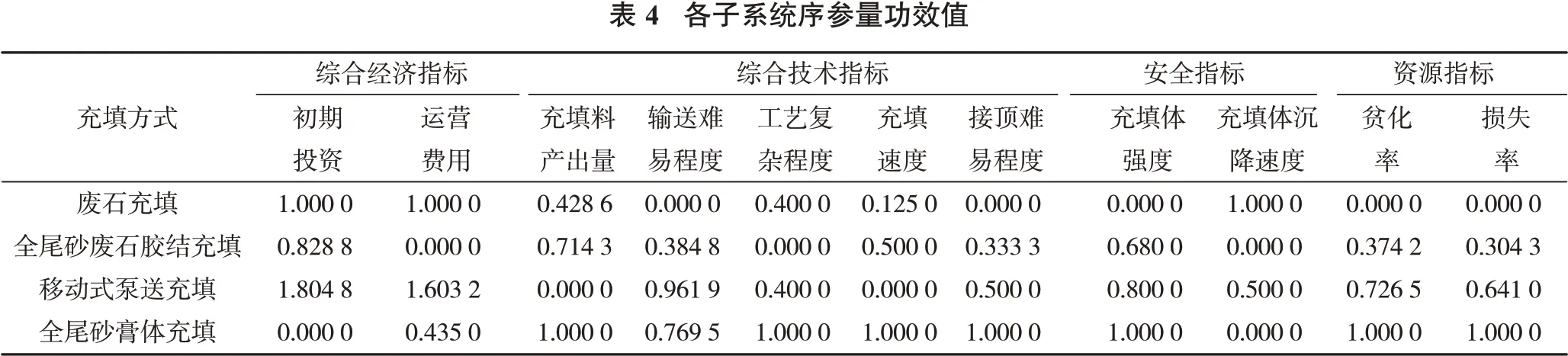
根据式(1)计算各子系统序参量的功效值,值得注意的是损失率、贫化率、采切比和采矿成本属于成本型序参量,应按负功效的计算式来计算,得到的各子系统序参量功效值见表4。
2.1.5 系统有序度计算
利用式(3)计算充填各子系统以及充填大系统有序度(表5)。

2.1.6 开采大系统的协同度计算
利用式(4)计算开采大系统即资源—技术—经济—安全系统的协同度(表6)。

2.2 测度模型结果分析
利用协同度测度模型,对废石充填方式变革到全尾砂废石胶结充填方式、全尾砂膏体充填的充填方式、移动式泵送充填方式的协同度进行测度,得到了充填系统中资源、技术、经济、安全各子系统及充填大系统的有序度和协同度。
(1)通过表5 可知,膏体充填的安全、技术、资源有序度为最大值,因为其初期建设投资费用搞,导致经济子系统有序度最低,但技术、安全、资源子系统对充填方式协同度的贡献度,明显大于全尾砂废石胶结充填和移动式泵送充填,使得膏体充填方式向协同有序的方向发展。
(2)通过表5 可知,从废石充填发展为全尾砂废石充填、移动式泵送充填到全尾砂膏体充填3种充填方式,各充填方式大系统有序度值为(0,0.075,0.072,0.187),有序度值呈现正增长趋势,表明上述充填方式的演变具有一定正协同度,说明从废石充填到全尾砂废石胶结充填再到膏体充填处于协同发展状态,但协同度峰值不高,仅为0.187,这与膏体充填系统建设前期投资较高有很大的关系,表明有效降低膏体充填系统建设投资,将进一步提高膏体充填开采系统的整体协同开采水平。
(3)通过协同度测度模型的建立,从经济、技术、安全、资源多指标综合分析可知,从废石充填变革到膏体充填方式,协同度达到了0.766,协同程度高,表明膏体充填为未来充填方式的发展方向。
3 结论
本研究运用协同学的理论,建立充填系统有序度模型和协同度测度模型,选择综合经济指标、综合技术指标、安全指标、资源指标等作为充填方式的子系统。以湖南某金属矿山从废石充填方式变革到全尾砂废石胶结充填、移动式泵送充填以及全尾砂膏体充填为例,通过有序度模型得出经济、技术、安全、资源各子系统以及充填大系统的有序度值分别为(0.250 6,0.150 0,0.438 2,0.030 2)、(0.102 6,0.278 6,0.138 0,0.575 9)、(0.043 7,0.046 1,0.076 1,0.067 9)、(0.000 0,0.016 6,0.033 3,0048 3)、(0.000,0.075,0.072,0.187),充填大系统的有序度值的变化说明该从废石充填到全尾砂废石胶结充填再到膏体充填处于协同发展状态,但有序度值不高,仅为0.187,这与膏体充填系统建设前期投资较高有很大的关系,表明有效降低膏体充填系统建设投资,将进一步提高膏体充填开采系统的整体协同开采水平。
通过协同度测度模型,得出充填方式演变的系统协同度为(0.000,0.295 6,0.288 7,0.766 0),从废石充填变革到膏体充填方式,协同度达到了0.766,表明膏体充填为未来充填方式的发展方向。
