多连杆悬架硬点坐标和衬套刚度优化分析
2021-06-02张翔叶宇翔
张翔,叶宇翔
(200093上海市 上海理工大学 机械工程学院)
0 引言
近年来,由于多连杆悬架设计灵活,多个杆件能很好约束车轮运动方向,被广泛应用在汽车后悬架上。悬架K&C特性是影响整车的操纵稳定性和平顺性关键性因素,而悬架的硬点坐标、衬套刚度又是影响悬架运动学特性和弹性运动学特性的重要因素,因此,如何合理巧妙地布置多连杆悬架的硬点坐标来提升K特性,如何恰当设计衬套各个方向上的刚度来提升C特性对整车性能的提升至关重要。
1 多连杆悬架多体动力学模型
本文以某轿车多连杆后悬架为研究对象。此悬架通过多个杆件的组合来把车轮与车身相连,此形式不仅可以让工程师设计更加灵活[1],还能通过杆件增加多个方向的约束,在满足汽车平顺性的基础上,更好地完成车轮操稳性目标。图1为在ADAMS/Car里建立的多连杆后悬架多体动力学模型。表1为该多连杆悬架主要硬点坐标。

图1 多连杆悬架多体动力学模型Fig.1 Multi-body dynamics model of multi-link suspension

表1 多连杆悬架的硬点坐标Tab.1 Hard point coordinates of multi-link suspension
2 多连杆后悬架运动学特性优化
2.1 优化模型的集成
本文以iSight为优化平台,利用Data Exchanger组件进行悬架硬点参数的交换,利用Simcode组件运行批处理文件,让ADAMS/Car多体动力学模型做轮跳行程为±50 mm平行轮跳试验并输出试验结果[2],利用MATLAB组件进行K&C特性指标的计算。搭建的多连杆后悬架硬点坐标DOE分析模型如图2所示,多目标优化模型如图3所示。

图2 多连杆后悬架硬点坐标DOE模型Fig.2 DOE model of hard point coordinates
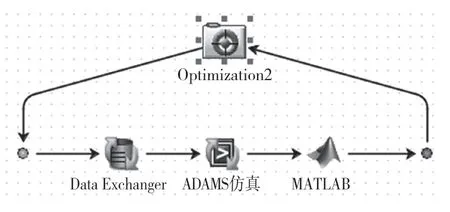
图3 多连杆后悬架硬点坐标多目标优化模型Fig.3 Optimization model of hard point coordinates
Isight集成ADAMS需要编写(.bat)启动文件和(.cmd)运行控制文件。(.bat)文件内容包含启动ADAMS,选择ADAMS/Car模块,选择Car的运行模式,选择批处理方式,输入命令控制文件。本文编写的多连杆悬架硬点优化(.bat)批处理文件内容如下:

2.2 灵敏度分析
由于多连杆悬架的硬点较多,把每个硬点当做设计变量的计算量是巨大的。通过DOE实验设计,找到对车轮定位参数、轮距、轴距影响较为显著的悬架硬点坐标,这样不仅能够减少优化时的工作量,而且还能保证优化的有效性。本次实验选取了多连杆悬架机构9个硬点的X,Y,Z坐标值,以多连杆悬架做上下行程为±50的平行轮跳过程中前束角、外倾角、轮距变化量、轴距变化量的最大值为优化响应目标。在iSight软件DOE组件中,选用参数试验(parameter study)工具,根据工程经验设定每个硬点坐标的扰动范围为-5~5 mm,分析结果表明硬点坐标UCA_inner_z,TOE_link_inner_z,UCA_outer_z,TOE_link_outer_z,UCA_outer_x,UCA_inner_x,LCA_inner_z,LCA_outer_z,trailing_arm_front_z,TOE_inner_x,TOE_link_inner_y对响应目标较为显著,具体灵敏度如表2所示。

表2 硬点坐标对各参数灵敏度的影响Tab.2 Effect of hard point coordinates on different characteristics of suspension
2.3 多连杆后悬架硬点坐标多目标优化
多目标优化首先需要确定哪些悬架性能参数作为优化目标和确定哪些悬架硬点坐标作为优化变量,然后设置约束条件,建立多连杆悬架多目标优化问题,选择合适的寻优算法,最后得到优化的结果。
2.3.1 目标函数与设计变量
为了减少轮胎磨损,提高车轮行驶的稳定性,在车轮相对于车身跳动过程中,一般希望前束角、外倾角变化范围尽可能小,希望前束角变化量在±0.1°之内,外倾角变化量在±2°之内[3]。车辆在行驶过程中,轮距和轴距的变化量过大会加剧轮胎的磨损,有时甚至会造成车辆失稳,因此在车轮相对于车身运动的过程中,希望轮距和轴距的变化量尽可能小。本文以多连杆悬架做上下行程为±50的平行轮跳过程中前束角、外倾角、轮距、轴距绝对值的最大值为优化目标,选取通过灵敏度分析得到的对响应目标影响较为显著的11个硬点坐标为优化变量。多目标优化的数学描述如式(1)所示。
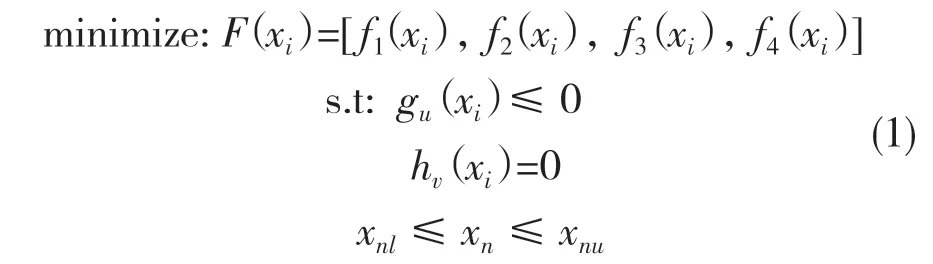
式中:f1(xi),f2(xi),f3(xi),f4(xi)——输入第i组硬点坐标后的前束角绝对值的最大值、外倾角绝对值的最大值、轮距绝对值的最大值、轴距绝对值的最大值;gu——u个不等式约束;hv——v个等式约束;xnl——多连杆悬架各硬点坐标的最小值;xnu——多连杆悬架各硬点坐标的最大值。
2.3.2 约束条件
本文选取了对响应目标较为显著的11个硬点坐标为优化变量,初始硬点坐标如表1所示,允许硬点坐标变化量的范围为-5~5 mm。
本文采用的优化算法为非支配排序遗传算法(NSGA-II)。在非支配排序中,NSGA-II算法选择接近Pareto前沿的个体,增强Pareto前进能力,所以具有良好的探索性能。本文NSGA-II算法参数设定为12个种群个体,进化代数为20代,交叉概率为0.9。运行多目标优化模型,优化模型收敛并得到Pareto最优解[4]。优化前和优化后的硬点布置方案如表3所示。

表3 硬点坐标优化结果Tab.3 Optimization results of hard point coordinates
2.3.3 优化前后对比
将优化得到的硬点坐标重新输入到多连杆悬架ADAMS/Car多体动力学模型,进行轮跳行程为±50 mm平行轮跳试验,得到平行轮跳工况下多连杆悬架运动学特性参数曲线的变化情况。优化前和优化后悬架运动学参数曲线对比情况如图4所示。
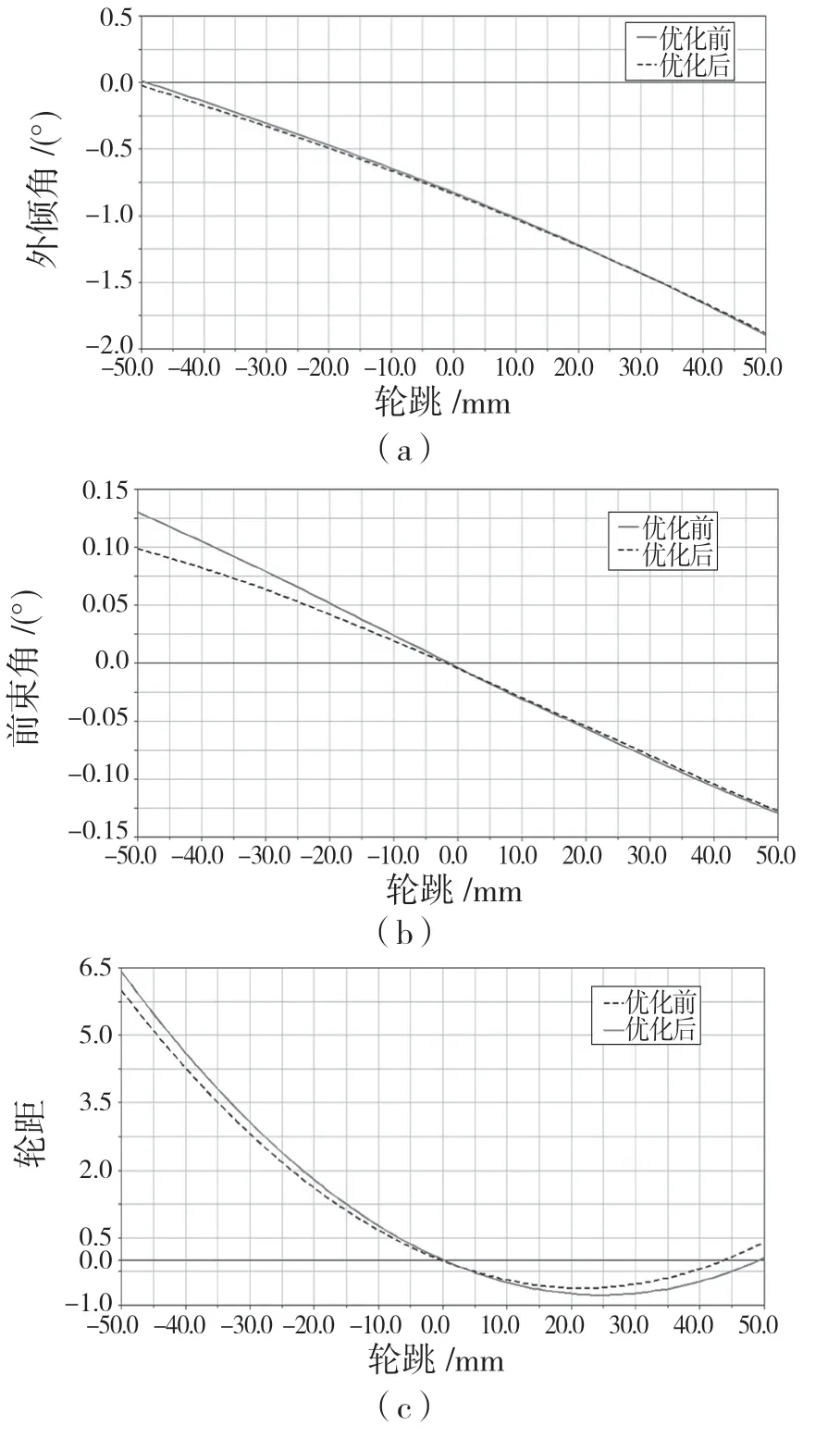
由图4可知,与优化前相比,优化后的车轮外倾角、前束角、轴距、轮距变化范围和绝对值最大值都有所减小,优化后的多连杆悬架运动学特性得到明显改善。
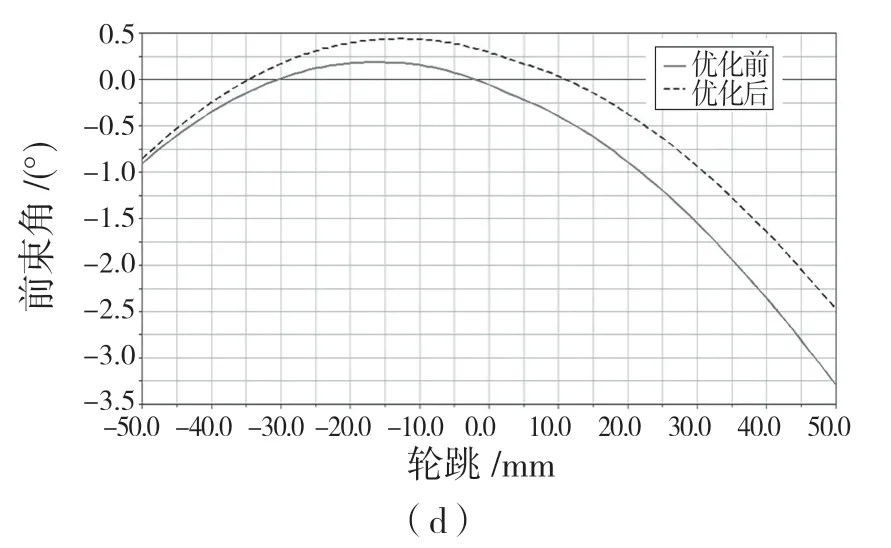
图4 优化前后悬架K特性随轮跳的变化Fig.4 Changes of suspension K characteristics with wheel hop before and after optimization
3 多连杆悬架弹性运动学优化
3.1 灵敏度分析
与硬点优化类似,多连杆悬架衬套刚度优化同样以Isight为优化平台,联合ADAMS和MATLAB搭建灵敏度分析模型和多目标优化模型,如图5、图6所示。
图5 多连杆后悬架衬套刚度DOE模型Fig.5 Stiffness DOE model of multi-link suspension bushing
图6 多连杆后悬架衬套刚度多目标优化模型Fig.6 Multi-objective optimization model for stiffness of multi-link suspension bushing
选择衬套的3个方向的线性刚度和扭转刚度为设计变量,衬套刚度缩放系数为0.5~2倍。在回正力矩工况下选择前束角变化率;在纵向力加载工况下选择前束角、外倾角、车轮纵向位移变化率;在侧向力工况下选择前束角、外倾角、车轮侧向位移变化率为响应目标。进行灵敏度分析,得到对目标值影响较为显著的7个设计变量如表4所示。
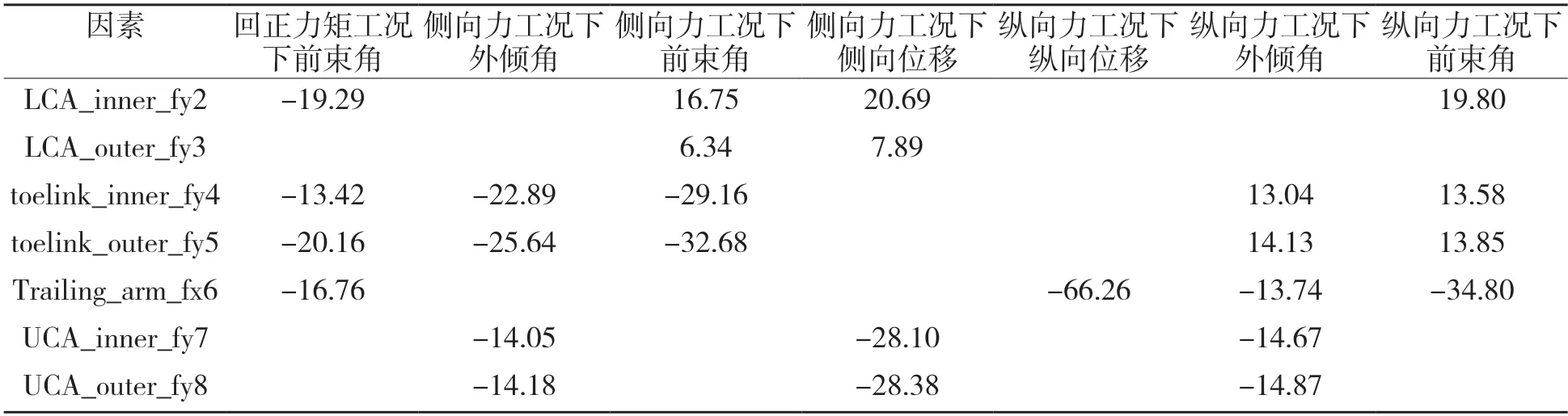
表4 衬套刚度对各参数灵敏度的影响Tab.4 Influence of bushing stiffness on sensitivity of various parameters
3.2 多连杆悬架衬套刚度多目标优化
多连杆悬架弹性运动学优化主要针对衬套刚度的优化,优化方法与硬点优化方式一样,以通过灵敏度分析得到的对目标值影响较为显著的7个变量为优化变量[5],衬套刚度的缩放系数为0.5~2倍。优化后,LCA_inner_fy为初始值的1.81倍,LCA_outer_fy为初始值的1.65倍,toelink_inner_fy为初始值的1.90倍,toelink_outer_fy为初始值的1.48倍,Trailing_arm_fx为初始值的1.99倍,UCA_inner_fy为初始值的1.17倍,UCA_outer_fy为初始值的1.89倍。
3.3 优化前后对比分析
将优化得到的衬套刚度数据写入多连杆悬架衬套属性文件,在ADAMS中进行回正力矩加载、纵向力加载、侧向力加载仿真。图7为优化前后的性能参数对比。
由图7可知,在纵向力工况下,优化后多连杆后悬架的前束角、外倾角、轮心纵向位移的最大值和变化范围都变小;在回正力矩工况下,优化后的多连杆后悬架前束角变化范围减小;在侧向力工况下,优化后的多连杆悬架前束角、外倾角、轮心侧向位移的最大值和变化范围都变小。悬架的弹性运动学特性得到优化。
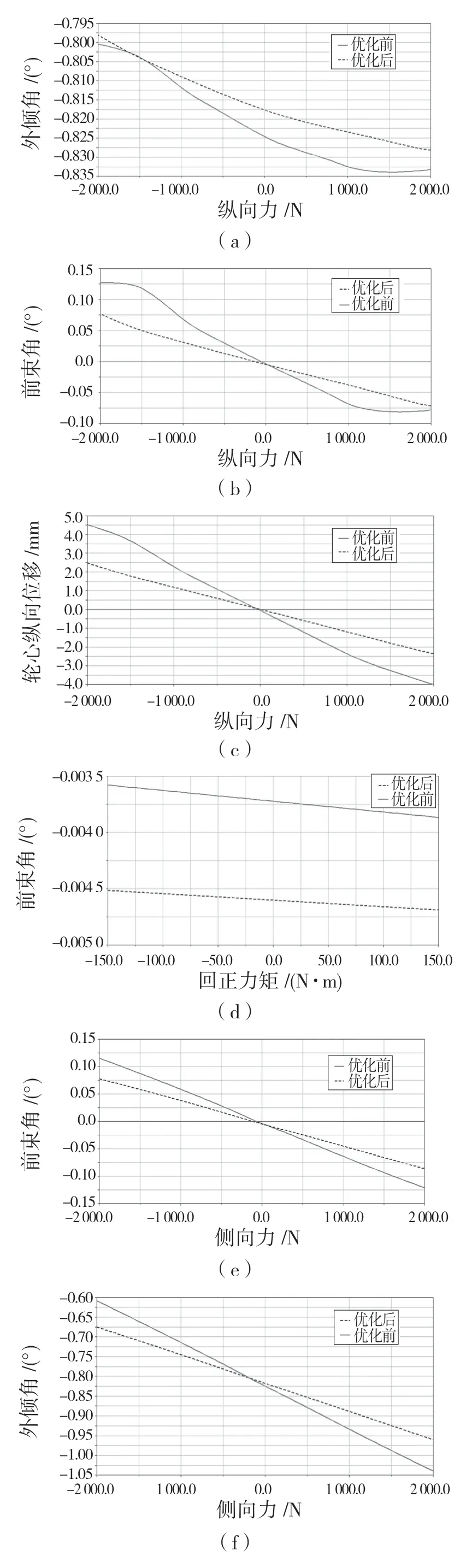
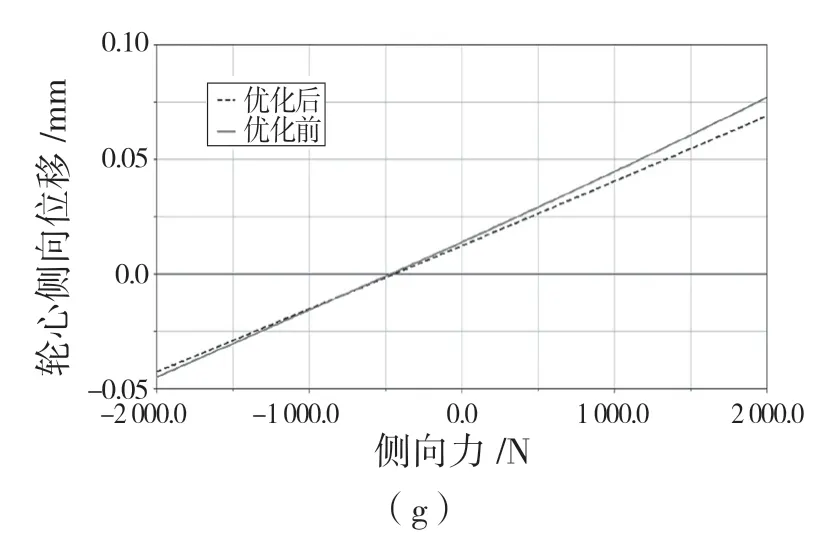
图7 优化前后悬架C特性随力加载的变化Fig.7 Changes of suspension C characteristics with force loading before and after optimization
4 结语
本文通过ADAMS,iSight和MATLAB联合仿真,首先,对硬点坐标和衬套刚度进行灵敏度分析,筛选了对K特性和C特性影响较大的硬点坐标和衬套刚度,然后,选用NSGA-II算法对悬架硬点坐标和衬套刚度进行多目标优化。优化结果表明,在车轮进行上下平行轮跳过程中,多连杆悬架的前束角、外倾角、轮距、轴距变化的范围和最大值都有一定程度的减小;车轮在受到侧向力、纵向力回正力矩时,车轮前束角、外倾角、轮距、轴距变化范围减小。多连杆悬架的运动学和弹性运动学特性得到优化。
