高岭土碟式分离机内部流场分析
2021-06-02崔建昆雷华泽王龙袁敏施钢
崔建昆,雷华泽,王龙,袁敏,施钢
(1.200093上海市 上海理工大学 机械工程学院;2.201906上海市 上海航发机械有限公司)
0 引言
高岭土矿是非金属矿类的一种,与云母、石英以及石灰石并称四大非金属矿[1]。高岭土有很多精良的物理性质和化学性质,因此,被开采加工并应用于各行各业[2]。在高岭土的生产工艺中,分级处理是必不可少的工艺流程之一,而离心机则是比其他分级设备更高效的分级设备,因此,通过对离心机的研究与设计可有效提高高岭土的分级处理质量,从而提高其利用率及产品质量。
1 分离机转鼓内流场模型建立与前处理
1.1 建模与网格划分
由于数值模拟的对象是碟片间隙内流场,因此,需要根据碟片模型建立出内流场模型,本文选取15层碟片间隙内流场建立模型。原碟片模型上设有筋条,但由于碟片间间隙较小,即碟片间流体的间隔较小,且筋条较细长,这样会增加网格划分的难度并且在前处理过程中很难选取每一层流场中流体流经筋条的面。综合考虑,选择对碟片上的筋条进行简化处理,以便提高计算效率,最终如图1所示。

图1 碟片内流场简化模型Fig.1 Simplified model of flow field in disc
本文选择采用Multizone(多区)网格划分方法,这种网格划分方法是基于ICEM CFD Hexa程序块,能将目标区域划分为多个可以扫掠或自由划分的区域,自行判别区域从而生成高质量的六面体网格,对达不到要求的区域使用非结构化网格进行划分,更好地提高了网格划分的质量和效率。如图2所示为碟片间的流场的网格划分后的模型,网格节点数量为5 266 752,单元数量为4 240 620。
图2 网格划分结果Fig.2 Meshing results
1.2 Fluent边界条件及计算参数设置
由于本文研究的碟式分离机用以分离高岭土颗粒,物料属于固液混合物,为获得颗粒的分离效率以及颗粒在高速旋转分离时的路径,选择离散相(DPM)计算模型用于计算。当粒子与壁面产生接触碰撞时,一般有以下几种情况:粒子出现弹性或者非弹性反射、穿过间断面区、逃逸,这时的轨迹计算终止、在接触时被捕集等。Fluent可以监控离散相粒子的轨迹,利用在笛卡尔坐标系下粒子各作用力的微分方程来求解其轨迹[3-4]。
在笛卡尔坐标系下,粒子作用力的平衡方程(X方向)如下[5]:

式中 :ul——流体相密度;ug——颗粒速度;μ——流体动力粘度;ρg——颗粒密度;dg——颗粒直径;Re——相对雷诺数;FD(ul-ug)——颗粒的单位质量拽力;CD——拽力系数。对于球状的颗粒物,在一定的Re范围内,a1,a2,a3——常数。
运用离散相模型,在入口处放入5束粒子,粒子直径分别为1,2,5,8,10 μm,定义粒子材料及总体流速,更新离散相模型的每次流程迭代,迭代步数最大为50 000步,步长因素为5,各粒径粒子的质量流量值为4.47 kg/s。计算域材料采用的是高岭土浆料,高岭土混合液的固相密度为2 600 kg/m3,液相密度为1 000 kg/m3,物料密度为1 240 kg/m3。碟片间流场模型转速为4 800r/min,进口采用速度进口为1.06 m/s。已知入口速度且为低速流动,选择入口速度边界条件,设置入口速度为1.06 m/s,入口湍流强度为1%,水力直径即孔径为0.03 m。设置压力出口压强为0 Pa,回流强度若不合适容易导致计算结果发散,回流湍流强度为1%,出口为环形横截面,根据水力直径公式可以计算出水力直径为0.006 8 m。流体与碟片接触壁面选择标准壁面,无滑移边界条件。本文所仿真的流体属于两相流,因此,选择Coupled算法进行计算,压力项与力矩选用2阶离散格式,湍流动能以及耗散率等均选择1阶离散格式。
2 流场分析
2.1 压力场分析
根据以上参数设置,可以得到碟片间壁面的压力分布仿真结果。在分析软件Fluent里,碟片间内流场的压力分布可以通过静压来反映[6]。如图3所示为转鼓转速为4 800 r/min时,碟片间的离心液压分布情况,图3(a)为15层碟片整体的压力分布云图,图3(b)为X=0 mm截面的各层碟片间流场压力分布云图。由压力分布云图可以看出,压力呈中心对称,碟片半径最大处压力最大,随着碟片半径的减小压力逐渐减小。根据最大离心液压pc的基本公式

图3 碟片内流场压力分布云图Fig.3 Cloud diagram of pressure distribution in flow field in the disc

式中:ρ物——物料密度,kg/m3;ω——转鼓角速度,rad/s;r1——碟片小端半径,m;r2——碟片大端半径。
由式(4)可以看出,离心液压pc的大小与混合物的密度、转鼓角速度以及碟片的半径有关,混合物密度和转鼓角速度一定时,离心液压pc是随碟片半径增大而增大。从图3中可以看出,仿真结果符合离心液压的公式规律,且当半径相同时,每一层的压力值变化不大。
当r1=0.08 m,r2=0.212 mm,ρ物=1 240 kg/m3,ω=502.65 rad/s时,根据公式计算碟片最大半径处的理论压力为6.0×106Pa。从图3中可以看出,最大半径处的压力为4.39×106Pa,低于理论离心液压,约为理论离心液压的73%。为了更好地验证各碟片间压力分布的仿真值符合离心液压的基本规律,现选取第8层碟片间内流场,对不同半径处的仿真值进行拟合处理,并与实际仿真值进行对比。由图4可以看出,仿真值与理论值分布趋势基本一致,都是呈二次分布,且随着半径增大离心液压也增大。而不同半径处的仿真值均低于理论值,这是因为液体在碟片间流动的时候存在着一定的滞后性,且随着半径的减小,滞后现象越来越小。

图4 不同半径处离心液压分布Fig.4 Centrifugal hydraulic distribution at different radii
从图3和图4的对比中可以看出,各碟片间的压力分布符合离心液压的基本规律,且仿真值与理论值相差不大,由此可知,利用有限元模拟仿真碟片间内部流场压力分布是可行的。经过模拟仿真分析可知,高速转动的碟片间混合物流动存在滞后性,以及物料刚进入碟片随着旋转流动时,物料不能得到及时的扩散。
2.2 速度场分析
碟式分离机转鼓内物料的周向速度反映了物料旋转的快慢,理论周向速度可以根据公式算出:v=ωr。图5(a)为碟式分离机碟片间内流场速度分布云图,图5(b)为X=0截面处的速度分布云图。可以看出,碟片间流场的速度随着碟片半径的增大而增大,当碟片半径最大时,即r=0.212 mm时,根据理论公式求得最大速度为106.56 m/s。仿真所得最大速度为106 m/s,略低于理论速度值,入口处仿真速度值低于理论值,这是由于高速旋转过程中,物料在碟片间存在滞后现象。从图6的速度矢量图中可以更立体、清楚地看出速度的分布情况,碟片半径最大处速度最大,且入口处的速度分界不是很明显,进一步证明了入口处可能存在物料滞后现象。

图5 速度分布云图Fig.5 Speed distribution cloud

图6 内流场速度矢量图Fig.6 Inner flow velocity vector
为了更好地验证各碟片间速度分布的仿真值符合理论周向速度的基本规律,同样选取第8层碟片间内流场,对不同半径处的仿真值进行拟合处理,与实际仿真值进行对比,如图7所示。从中可看出,不同半径处的仿真值与理论值分布趋势基本一致,且速度随着半径的增大而增大,进一步验证了仿真所得的速度分布规律基本符合理论周向速度分布的基本规律,验证了仿真方法的合理性。

图7 不同半径处速度分布Fig.7 Velocity distribution at different radii
2.3 湍流动能分析
湍流动能可以判断湍流的发展和衰退,可以通过湍流动能判断出流体流动过程中是否有湍流现象发生。湍流动能k可以用湍流强度I表示为

式中:uavg——平均流动速度,m/s 。
当湍流强度I高于10%,判定为高湍流强度,当其低于1%时,判定为低湍流强度。如图8所示为截面X=0 mm处湍流强度分布图。

图8 X=0 mm截面处总湍流强度Fig.8 Total turbulence intensity at X=0 mm section
从图8可看出,此时,设计参数下的碟式分离机的湍流强度最高达91.3%。且这种高湍流强度仅出现在流体刚开始进入碟片入口的通道处,但在流体从入口往上运动的湍流强度最高在14.1%~22.7%范围内,属于高湍流强度。这种湍流强度比较高的情况主要发生在前几层碟片间,可以判定为物料一开始未完全散开导致的。还有一处高湍流强度范围出现在出口处少许地方,也高达10%以上。碟片间隙中的湍流强度均在10%以下,说明了碟片间隙内基本为层流,与理论相符[7]。
2.4 分离效率分析
高岭土浆料中的颗粒粒径范围为1~20μm不等,本文选择1,2,5,8,10 μm粒径的颗粒进行分析,结果如图9、图10所示。通过压力和速度分布云图可以看出,流体沿碟片运动时要滞后于碟片,这种滞后也会使离心力减小[8]。在上述因素作用下,液流速度图形有较大变化,液体质点的运动轨迹与碟片母线不平行。

图9 各粒径颗粒分离轨迹总图Fig.9 General drawing of separation trajectory of particles with various sizes
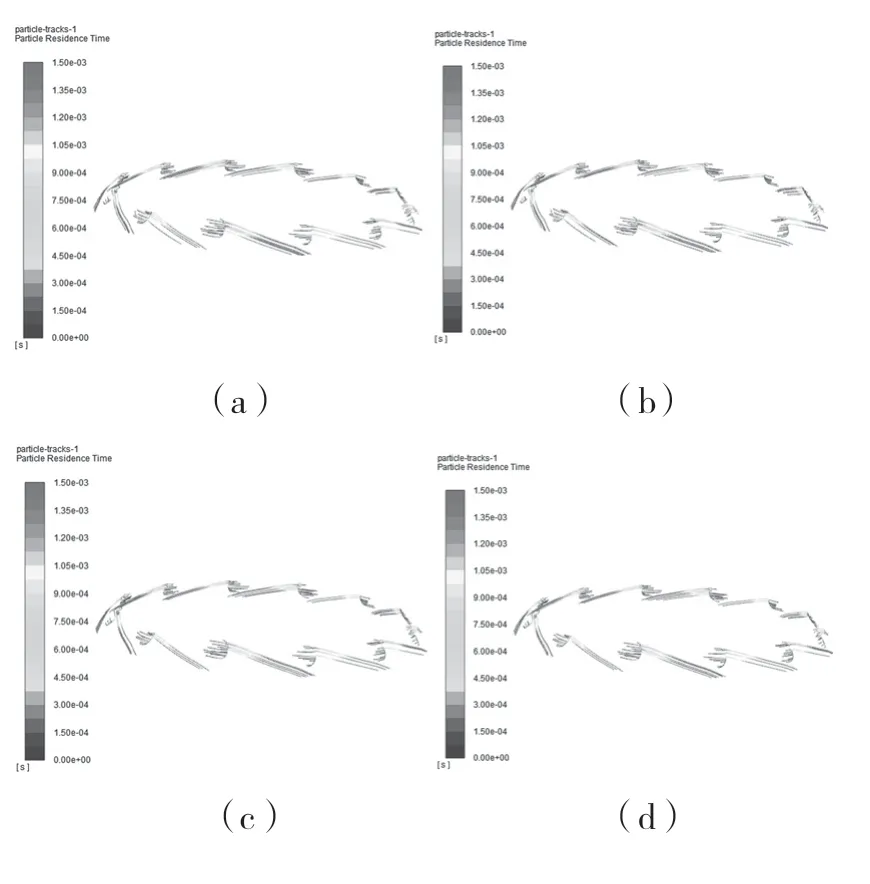

图10 各粒径颗粒运动轨迹图Fig.10 The trajectory diagram of particles of various sizes
为更准确地表示碟式分离机的分离效率,通过Fluent计算出不同粒径的分离情况,从而获得不同粒径的分离效率,计算可得1,2,5,8,10 μm粒径颗粒的分离效率分别为53.1%,60.6%,64%,66.5%,69.5%,将各粒径颗粒的分离情况进行统计,如图11所示。

图11 不同粒径颗粒分离效率Fig.11 Separation efficiency of particles with different particle sizes
3 结论
本文根据仿真得到所需压力分布云图以及速度分布云图,对比理论离心液压以及理论速度,验证了参数设置以及软件仿真的合理性。根据湍流强度分布云图分析,发现物料入口处湍流强度最大,以及出口处也存在湍流问题,但碟片间隙内的流场湍流强度较低,属于层流状态,符合理论分析。
分析计算得到DPF550分离机对所选范围内粒径颗粒的分离效率。其中物料颗粒粒径为1 μm的分离效果最差,10 μm分离效果最好,平均分离效率为62.74%左右,与实际运行效果基本一致。
