基于联合仿真与Haigh模型的连杆疲劳强度分析
2021-06-02周爱博孙嵩松张营
周爱博,孙嵩松,张营
(210037江苏省 南京市 南京林业大学 汽车与交通工程学院)
0 引言
相关资料显示,目前汽车发动机零部件的可靠性问题中,80%以上都是疲劳问题[1],造成这一现象的主要原因是,汽车发动机在运行过程中,一些关键零部件如连杆、曲轴等会受到来自不同激励源的交变载荷的持续作用[2-3],导致零部件的疲劳失效,并进而导致发动机乃至整车的失效。另一方面,作为发动机的关键零部件之一,连杆在工作过程中会受到非对称的拉-压交变载荷的持续作用。现有研究表明,构件在受到交变载荷时,其疲劳强度不仅与应力幅值有关,还受到应力比的影响,因此有必要针对连杆在给定拉压载荷比作用下的疲劳特性进行分析,以确定其在该工况下的疲劳安全特性[4]。
近年来,随着计算机软件的开发和利用,有限元法在零部件疲劳分析时得到了广泛的应用。本文采用该方法对某款六缸柴油机的连杆进行建模,并分析其在给定拉-压工况下的应力状态,在此基础上采用Haigh模型对其进行等效载荷的修正以及疲劳安全系数分析。研究表明,当采用42CrMo钢制备该型号的连杆时,能够满足额定工况下的疲劳强度要求,但是无法满足发动机增压后的疲劳强度要求。
1 连杆的建模以及网格划分
表1为连杆主要结构参数。该连杆为某国产六缸柴油机连杆,其中杆身、杆盖等部位的材料为42CrMo合金钢,表面强化处理工艺为渗氮;而轴瓦采用08号钢,表面强化处理工艺为滚压,二者相应的材料属性如表2所示。

表1 连杆主要结构参数Tab.1 Main structural parameters of connecting rod

表2 材料属性表Tab.2 Material properties
采用CATIA软件对该连杆的各个部件进行建模,并将其导入HyperMesh软件对其进行网格划分,相应的结果如图1所示。
该三维网格模型包括连杆的杆身、杆盖、螺栓、轴瓦以及曲柄销等部件,其网格单元类型为C3D10二阶网格,网格数量为87 951个。
2 连杆有限元分析
2.1 连杆受力分析
如图2所示,气缸的中心线经过曲轴的中心,其中O代表的是连杆,AB代表的是曲柄,B代表的是曲柄销中心,A代表的是连杆小头内孔径的中心点。当连杆绕着O点运动时,相应的惯性力为[5]
式中:Pj——连杆所承受的直线惯性力;mp,m1——活塞质量与连杆只做直线往复运动部分的质量。
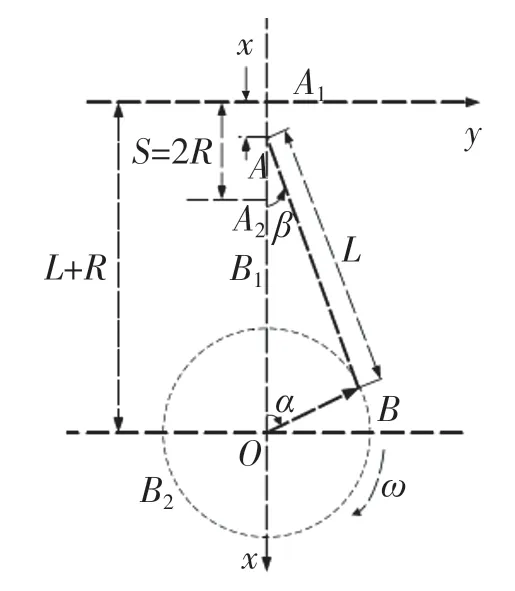
图2 连杆运动示意图Fig.2 Schematic diagram of connecting rod motion
当活塞运动到下止点时,该载荷即为连杆所受到的最大拉力;而当活塞运行至上止点时,连杆所受到的压力最大,相应的压缩力为

式中:PY——压缩力;Pz——活塞气体压力。本文中,连杆在标准工况下的最大拉伸以及压缩载荷分别为42.1,162.5 kN。
2.2 连杆接触定义
本文中,连杆不同零部件之间一共有8个接触对:连杆体与连杆盖之间的2个接触对、连杆体与上轴瓦之间的接触对、连杆盖与下轴瓦之间的接触对、上下轴瓦与曲柄销之间的2个接触对、以及上下轴瓦之间的2个接触对。将划分好的连杆三维网格模型导入ABAQUS软件平台,采用Tie约束设置连杆体与连杆盖之间的2对接触,同时采用面与面接触设置其余的6对。
2.3 载荷与边界条件定义
如图3所示,本文中连杆的拉压载荷都施加在连杆小头,通过将连杆小头中心与内表面耦合,从而将载荷施加至杆身。通过改变载荷的正负值,实现不同方向(拉-压)的加载。同时,采用位移边界条件,将曲柄销的两侧截面所有节点的自由度完全固定住,如图4所示。

图3 载荷施加点Fig.3 Reference points of load

图4 边界条件示意图Fig.4 Schematic diagram of boundary condition
2.4 有限元结果分析
采用上述有限元模型对连杆在拉压载荷工况下的应力应变状态进行分析,结果分别如图5、图6所示。
如图5、图6所示,最大拉伸工况下主要应力集中的部位是连杆小头和杆身连接的地方,相应的值为420 MPa;而最大压缩工况下应力最大值位于连杆小头内两侧,其值为641 MPa。

图5 拉伸工况下的应力云图Fig.5 Stress nephogram of tensile condition

图6 压缩工况下的应力云图Fig.6 Stress nephogram of compression condition
3 连杆疲劳强度分析
由有限元分析结果可以看出,连杆在受到额定交变载荷作用时,其应力状态并非对称,因此有必要采用平均应力对其进行等效载荷修正。现有研究表明,Haigh模型在修正金属零部件的高周疲劳特性时具有较高的精度,其表达式为[6]

式中:α——Haigh系数;S6——修正前的平均载荷;Sa1——修正到平均载荷的交变载荷,Sa2——修正前的交变载荷。
目前一些疲劳分析软件如Femfat已经集成了Haigh模型模块,采用该软件对连杆在99%存活几率下的疲劳安全系数进行分析计算,相应的结果如图7所示。
如图7所示,该连杆在标准工况下最小疲劳安全系数值为1.3,位于连杆小头与杆身连接处,满足大于1.1的极限要求,因此该连杆能够满足发动机在额定工况下的疲劳强度要求[7]。

图7 疲劳安全系数云图(标准工况下)Fig.7 Fatigue safety factor nephogram(under standard working condition)
4 增压可行性分析
近年来随着涡轮增压技术的应用,内燃机尤其是柴油机的爆压已经得到了极大的提升。本文中柴油机在标准额定工况下的爆压为14 MPa,而一些柴油机在实施涡轮增压之后爆压已经超过了20 MPa[8]。由连杆的受力分析可以看出,当爆压增大之后,连杆所受到的拉伸载荷并不受影响,但是压缩载荷会产生变化,因此有必要对增压后的连杆的疲劳安全性能进行分析,为发动机实施增压的可行性进行评估。采用相同的技术路线对发动机爆压增压至20 MPa后连杆的疲劳安全性能进行分析,相应的结果如图8所示。
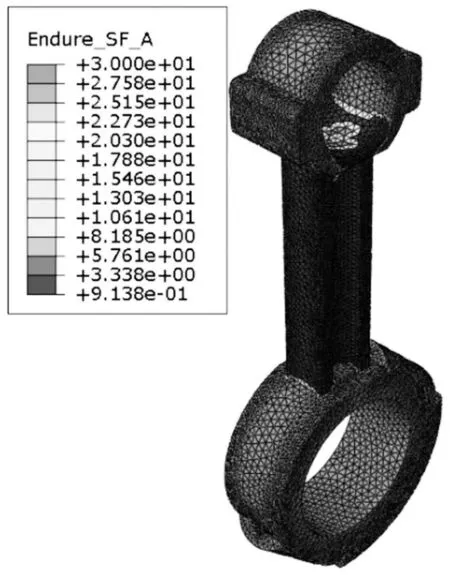
图8 疲劳安全系数云图(增压工况下)Fig.8 Fatigue safety factor nephogram(under supercharged working condition)
由图8可以看出,发动机的爆压增压至20 MPa之后,连杆的疲劳安全系数有了明显的下降,其中杆身的疲劳安全系数下降至不足1,已无法满足该工况下的疲劳强度的要求。
5 结论
针对某款连杆的疲劳强度要求,采用多种CAD以及CAE软件对其进行联合仿真,在此基础上采用Haigh模型对其高周疲劳安全性能进行分析。研究结果表明,该连杆能够满足额定工况下的疲劳强度要求,但是无法满足增压后的发动机的疲劳性能要求。
