考虑转运的新零售供应链订货模型及策略

（武汉理工大学 物流工程学院，湖北 武汉 430063）

0 引言

“新零售”是企业以互联网为依托，通过运用大数据、人工智能等先进技术手段，对商品的生产、流通与销售过程进行升级改造，进而重塑业态结构与生态圈，并对线上服务、线下体验以及现代物流进行深度融合的零售新模式[1]。其特点是：全渠道融合、多元化零售、供应链重构且柔性增强、强调消费者体验和销售效率提升[2-3]。

新零售重构了供应链，赋予供应链新的特征，与传统供应链相比，新零售下的供应链所面临的不确定性和风险更大。为了给消费者提供及时高效的服务，对供应链的灵活性、柔性要求更高。这些新特征使得供应链成员之间的冲突更加明显，因此需要对其进行协调。目前对于新零售供应链协调的研究主要是关于最佳订货策略。陈志刚等研究了零售商基于市场信息更新过程的二次订货模型，根据需求预测更新结果决定二次订货与否，分析了正常渠道订货和紧急渠道订货对零售商库存管理的意义[4]。王利华研究了由单一供应商和零售商构成的供应链模型，在传统报童模型的基础上，引入风险偏好和损失偏好，研究零售商的订货决策问题[5]。朱传波等引入条件风险值，构建突发事件风险规避下的企业订货策略模型及收益共享契约下的订货模型，分析供应商的可靠性以及零售商的风险规避程度对零售商最优订货量的影响[6]。吴胜等引入消费者的时间偏好，研究供应链定价与订货问题，分析强势供应商、强势零售商和供需双方势力均衡三种情况下的供应链定价及订货问题，并分析消费者的时间偏好对供应链定价、订货量及利润的影响[7]。

当前，转运是提高供应链柔性的一个有效方式，它不仅可以降低库存水平，还可以应对缺货问题并及时满足顾客需求，提高供应链的响应速度，进而提高企业的服务水平[8]。并且转运实施难度小、投入资源少，在企业供应网络不断扩张的趋势下，转运行为可以加强网络中各节点间的联系，实现网点间的资源协调，降低供应链的整体成本。但目前仅有少部分的文献把转运加入到新零售供应链的订货策略研究中，如Fuguo Zhao 利用转载价格协调了一个同时包含线上线下零售渠道的二阶供应链模型[9]。

综上，把转运考虑到新零售供应链订货模型中的研究较少，因此探究转运与否、转运价格对新零售供应链最优订货策略以及最优利润的影响，不仅可以丰富这一领域的理论知识，而且研究结果可为新零售供应链成员的决策提供参考依据，具有理论价值和现实意义。本文以新零售供应链为研究对象，分别构建无转运和考虑转运两种情况下的新零售供应链订货模型，求解出最佳的订货量。在模型的基础上分析转运对零售商订货量和利润的影响，最后通过实例仿真检验模型的科学性以及定理的可靠性。

1 问题描述、符号说明和基本假设

1.1 问题描述

本文是以一个供应商和销售同一商品的两个新零售门店M、N 构成的供应链为研究对象，其中零售门店M，N完全对称，新零售环境下，供应链的基本结构如图1所示。在该系统中，每个零售门店的总需求Di服从非负、连续的密度函数f(x)和分布函数F(x)。消费者的全渠道需求均由零售门店满足，其中其“线上下单，店铺配送”需求占总需求的比例为α，“线下需求”占总需求的比例为β，“线上购买，线下自提”的需求占总需求的比例为χ，α+β+χ=1。三种需求无优先级，按照到达的先后顺序被满足。

图1 新零售供应链的基本结构图

在销售季初，两个零售门店以相同的批发价格各自向上游供应商订货，供应商的供应能力无限。在不考虑转运的情况下，M 和N 之间是相互独立的，彼此之间的转运量为零。在考虑转运的情况下，两零售门店之间的库存可以共享，即两零售门店M，N在事前签订契约，约定当其中一个零售商缺货，而另一零售商有多余库存时，库存多余的零售商向库存短缺的零售商转运库存，并约定转运价格。在销售期结束后，当零售门店库存有剩余时，商家以价格s处理剩余库存；当零售门店库存不足时，每单位商品承担价格为v的缺货损失。

转运会影响零售商的库存，但是转运以及转运价格对零售商的订货量和利润是否有影响、是否存在最佳的转运价格等问题是需要进一步探究的，本文即是对这些问题的研究。

1.2 符号说明和基本假设

对新零售供应链订货模型构建中涉及的符号进行说明，具体见表1。

表1 符号说明表

为了确保决策的科学性和分析的简便性，对模型做出如下假设：

（1）假设零售门店i的随机需求Di服从[0，h]上的均匀分布,且Di相互独立。

（2）两个零售门店的期初库存为0，有且只有一次订货机会，且订货数量无限制，订货货物在销售初期送至零售门店。

（3）当店铺缺货时，货物由有多余库存的零售门店转运至缺货的零售门店。

（4）由于转运是同城转运，转运所需时间较短，假设转运过程中订单不流失。

（5）假设零售门店依据期望利润最大化的原则来进行决策，即为风险中性和完全理性。

2 新零售供应链订货模型的构建

报童模型是供应链管理中的经典模型，主要用于讨论需求不确定条件下的订货量决策问题，因此本文采用了连续随机需求的报童模型，构建无转运时的新零售供应链订货模型，在此模型的基础上引入转运变量，对考虑转运时的新零售订货量进行决策。

2.1 无转运时的新零售供应链订货模型

在该模型中，零售门店N 和M 之间是相互独立的，转运量为零，属于连续随机需求的报童模型。建模的思路是计算出无转运时新零售供应链中各渠道销售量的期望值，在此基础上构建利润函数，以利润最大化为目标，通过求利润对订货量的偏导数，得到偏导数为零的点即为最优订货量模型。

（1）期望销售量计算。根据报童模型，可以得到零售门店i 的期望销售量式（1），“线上下单，店铺配送”需求的期望销售量式（2），“线上购买，线下自提”需求的期望销售量式（3），“线下需求”的期望销售量式（4）。

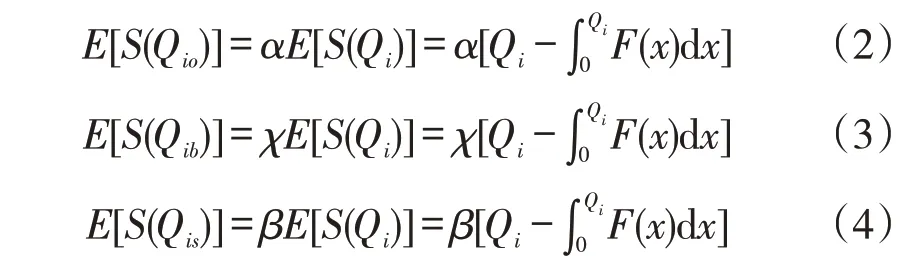
（2）新零售门店利润函数构建。由于零售门店M，N 完全对称，故选取零售门店N 进行研究。当不存在转运行为时，考虑其残值和缺货损失，零售门店N的利润函数见式（5）。

其中p·E[S(QN)]为销售收入，b·αE[S(QN)]为“线上下单，店铺配送”部分需求的配送成本，s·max(QN-x,0) 为销售期末剩余产品的残值，v·max(x-QN,0)为销售期末由于库存不足造成的缺货损失，w·QN为产品的批发成本。

（3）求解最优订货量。将式（5）展开得到不转运时零售门店N的利润函数式（6）。

对式（6）求关于QN的一阶偏导得到式（7），令其等于0，得到式（8）。

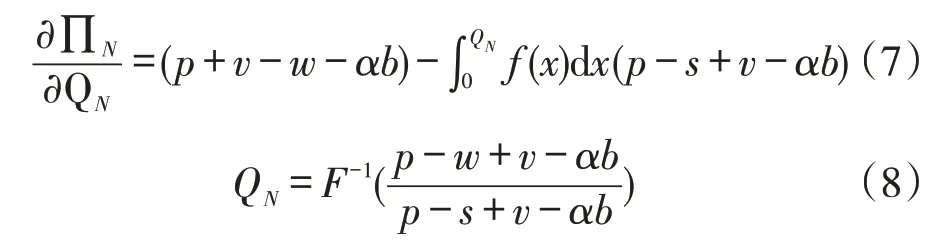
2.2 考虑转运的新零售供应链订货模型

该模型考虑了零售门店N 和M 之间的转运行为，具体结构如图1所示。进行转运的新零售门店M和N进行非合作静态博弈，即在信息缺失的情况下，两个零售商会各自考虑自身的最大利润，而某一方的利润会受另一方订货决策的影响，因此本节将根据两新零售门店的利润函数，求其纳什均衡订货量。

2.2.1 转运量的计算。为了方便理解，本节首先分析了两零售门店的库存与需求之间的关系，可以将其划分为六种情况，如图2所示。

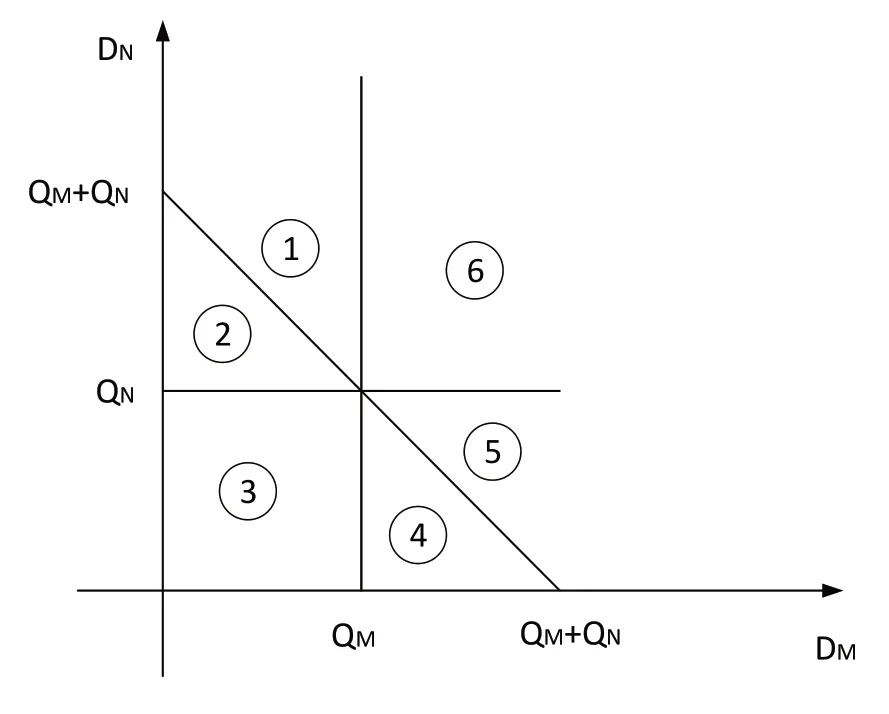
图2 新零售门店M和N的库存与需求关系

然后在此基础上对新零售门店M,N之间的转运量进行分析和计算，具体见表2。表2的六个事件与图2的六种情况一一对应。

⑥查询维修人员。对于刚刚维修不久的机井，可以询问维修人员，专业维修人员可以通过设备的大小、节数、粗细及型号印象，判断出具体型号。

基于需求的分布函数，对表2中的六种情形下的转运量进行计算。其中事件3、6 的转运量为0；事件1、2为新零售门店M向N转运，记转运量为TMN；事件4、5为新零售门店N向M转运，记转运量为TNM。

（1）TMN的计算

①当xN-QN ＜QM-xM时，转运量为TMN=xN-QN，转运后零售门店M有剩余，存有剩余残值。

② 当xN-QN＞QM-xM时，转运量为TMN=QM-xM，转运后零售门店N仍缺货，存在缺货损失。

综合以上分析，得出新零售门店M 向新零售门店N转运的转运量TMN，见式（10）。

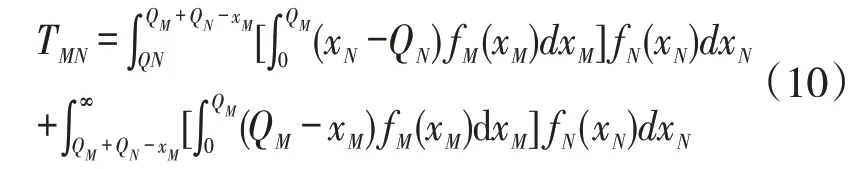
（2）TNM的计算

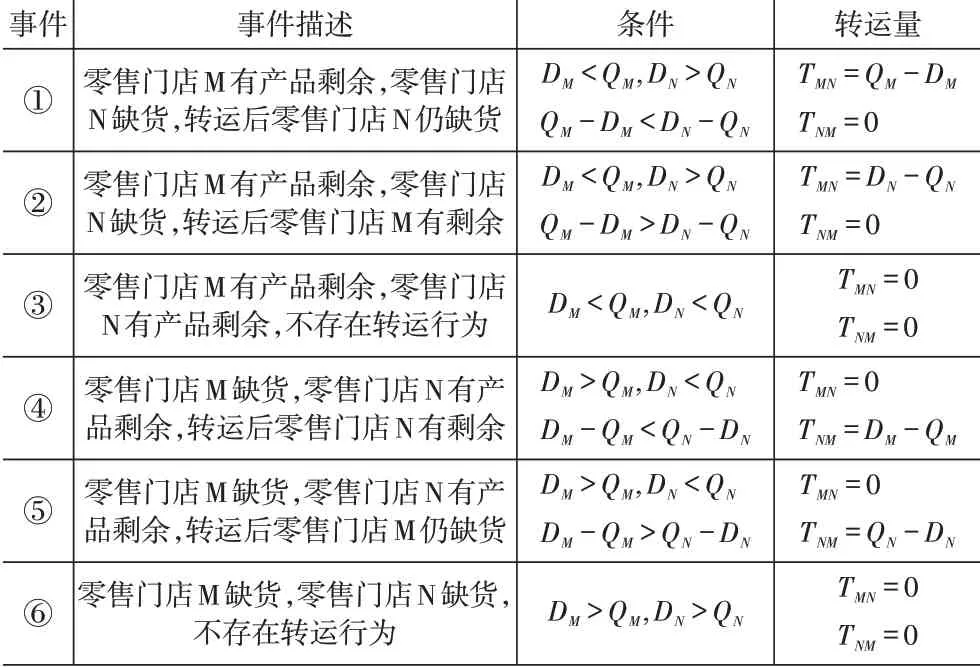
表2 转运时两零售门店之间的转运事件及转运量

①当xM-QM ＜QN-xN时，转运量为TNM=xM-QM，转运后零售门店N 有剩余，有剩余残值。

② 当xM-QM＞QN-xN时，转运量为TNM=QN-xN，转运后零售门店M仍缺货，存在缺货损失。

综合以上分析，得出新零售门店N 向新零售门店M转运的转运量TNM，见式（11）。

（1）利润函数的构建。与非转运时相比，转运时需要考虑转运部分产品的销售收入与成本。转运产品的售价与非转运相同为p。转运所造成的成本包括转运价格pt和转运过程中的运输费用bt，均由转入方承担。转运价格需高于转出方剩余商品的单位残值s，而低于转入方单位商品的边际收益与转运成本之差，边际收益即商品售价p与商品的单位缺货损失v之和，即s ＜pt ＜p+v-bt。基于以上的假设分析，得出新零售门店N的利润见式（12）。

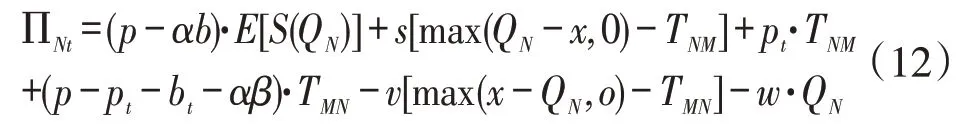
其中，p·E[S(QN)]为零售门店的全渠道销售收入，αb·E[S(QN)]为“线上购买，店铺配送”渠道需求的配送成本，s[max(QN-x,0)-TNM]为转运过后商家剩余产品的残值，pt·TNM为零售门店将剩余产品转运至缺货的商家所获得的转运收入，(p-pt-bt-αβ)·TMN为商家售卖转运进来的商品获得的利润，v[max(x-QN,o)-TMN]为零售门店在接受转运后仍然商品短缺所造成的缺货损失，w·QN为零售门店的批发成本。

将式（10）和式（11）代入式（12）展开得到转运时零售门店N的利润函数，见式（13）。

同理，由于两新零售门店完全对称，可以求得新零售门店M 的利润函数及其一阶导数，使其一阶导数等于0，并将两个公式联立，可以求得在静态非合作博弈状态下的新零售门店N的纳什均衡订货量见式（17），其中B=2(s-p-v+αb)+(pt-s)。

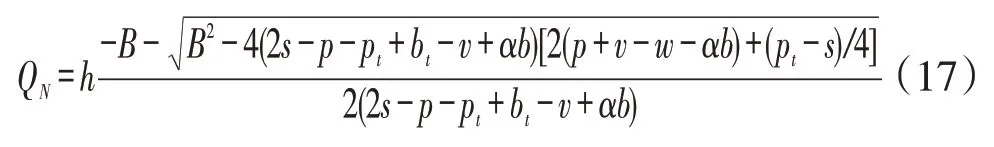
3 基于转运的新零售供应链订货策略分析

基于前文中构建的利润函数与最优订货量模型，进一步对其进行公式推导，发现转运可以提升供应链的利润，且在纳什均衡状态下，存在一个合适的转运价格使得供应链利润最大化，证明了转运行为对新零售供应链有协调作用。

3.1 转运前后的利润对比

定理一：转运后新零售门店的利润一定大于等于不转运的利润，即∏Nt≥∏N。

证明：化简式（13）可以得到式（18）。

而由于转运价格高于产品的剩余残值，转运后产品的售卖价格高于其售卖成本，故pt-s＞0,p-pt-bt-βb+v＞0，故(pt-s)·TNM+(p-ptbt-βb+v)·TMN≥0，所以∏Nt≥∏N。

故定理一得证。

3.2 转运价格对订货量的影响

定理二：零售门店M,N 的最优订货量随着转运价格的提高而增加，即。

证明：令

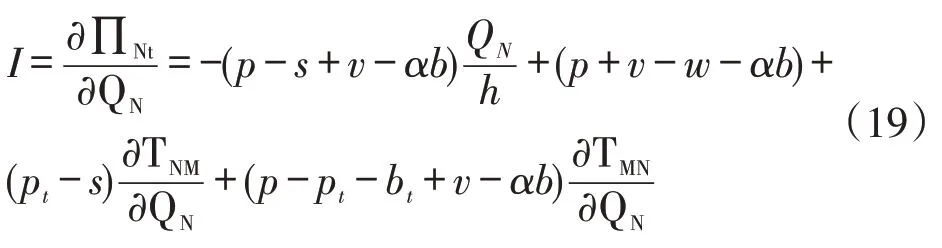
当处于均衡状态时，式（19）等于0，故根据隐函数的求导公式，求隐函数I(pt,QN)中订货量QN关于转运价格pt的导数，可以得到式（20）。

3.3 转运价格对利润的影响

定理三：在纳什均衡状态下，在[s,p+v]内，存在转运价格pt*使新零售环境下的零售门店N的利润达到最高。

证明：为了分析转运价格对于新零售门店pt均衡利润的影响，求得新零售门店利润对于转运价格pt的全导数，见式（27）。

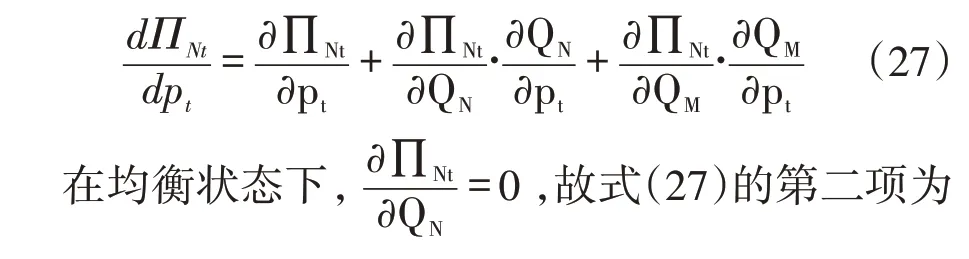
4 实例仿真分析

为了检验转运对零售门店的订货量以及利润的影响，运用A 企业的实际运营数据进行实证分析。假设两零售门店需求均服从（0,500）的均匀分布，其他参数见表3。

表3 参数取值

4.1 转运前后的最优订货量与利润对比分析

利用MATLAB软件进行数据仿真，得出表4的计算结果，对转运前后的最优订货量与利润进行对比分析。

（1）转运行为可以降低门店订货量，提升门店利润。通过表4可以看出在采取转运措施后，相较于非转运时，零售门店的订货量下降，利润大幅提升，这与新零售供应链订货模型得出的结论中定理一是相同的。

（2）新零售门店的最优订货量和利润对于是否转运较为敏感，对于转运价格的变化较为不敏感。对表4中的数据进行分析，以转运价格为35为例，相较于不转运时，最优订货量下降了14%，利润上升了93.5%。但是随着转运价格的提升，新零售门店的最优订货量和利润的变化虽然有所改变，但变化相对不明显。例如对转运价格为35 与转运价格为45 的两种情形进行对比，订货量上升了1.6%，利润上升0.5%。通过数据对比，说明新零售门店的订货量和利润对于是否转运比较敏感，但是对于转运价格的变化不太敏感。因此进行转运与否对新零售门店的订货量和利润影响较大，若两门店在转运价格协调不畅时，也仍建议采取转运行为。

表4 转运与非转运时零售门店的订货量与利润

4.2 转运价格对最优订货量及利润的影响

（1）转运价格对零售门店订货量的影响。通过图3 可以看出当转运价格提高时零售门店的最优订货量也随之增加，这与新零售供应链订货模型得出的结论中定理二是相同的。

图3 转运价格对订货量的影响

（2）转运价格对零售门店利润的影响。从图4可以看出，零售门店N 的利润随着转运价格的升高呈现先增后减的趋势，因此一定存在一个最优的转运价格，使得零售门店N 的利润达到最优，由图4 可知当转运价格为60时，新零售门店的利润达到最大，为6 360，这与3.3中定理三得出的结论是相同的。

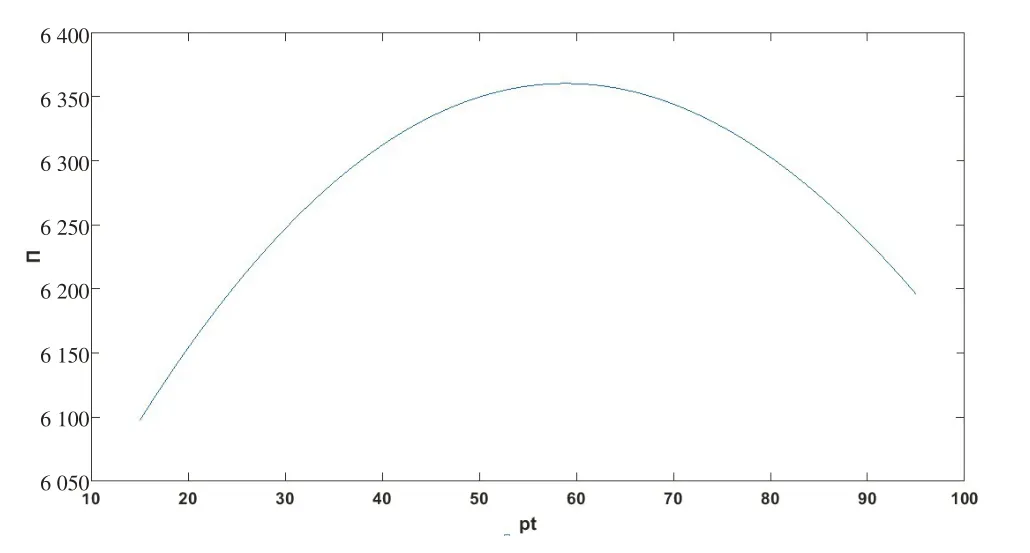
图4 转运价格对利润的影响

5 结语

在新零售背景下，供应链成员之间的冲突更加明显，需要对其进行协调，转运是供应链协调的有效方式。因此本文将转运行为加入到供应链订货模型的研究中。首先构建了无转运时的供应链订货模型，其次计算有转运时的转运量，在此基础上建立考虑转运的纳什均衡最优订货模型，分别求出了有转运和无转运时的最优订货量。在建模的基础上对模型进行进一步推导，分析了转运与否、转运价格对订货量以及利润的影响，得到了关于转运对零售门店订货量和利润影响的3个定理。最后通过MATLAB进行实例仿真分析，检验模型的可性和定理的可靠性。结果表明：（1）转运行为在解决缺货问题的同时，可以减少订货量，降低库存水平，提高利润。（2）当转运价格提高时，零售门店的最优订货量也随之增加。（3）零售门店的利润随着转运价格增加呈现先增后减的趋势，因此在纳什均衡下，存在一个最优的转运价格使得参与转运的两个零售门店获得的利润最高。