仿生气动肌纤维静态特性建模与实验研究
2021-06-01雷静桃张悦文戴臻豪徐子力
雷静桃, 张悦文, 戴臻豪, 徐子力
(上海大学 机电工程与自动化学院, 上海 200444)
气动人工肌肉因其与生物肌肉具有相似的柔顺性和收缩特性,被广泛应用于可穿戴机器人和仿生机器人.目前,德国FESTO 公司的DMSP/MAS型气动肌肉及日本Bridgestone公司的McKibben型气动肌肉是较为典型的气动人工肌肉,这类气动人工肌肉的直径范围为10~40 mm,两端是有一定长度的刚性防漏气接头元件[1],主要用于工业柔性机器人、外骨骼机器人、医用康复机器人及中型仿生机器人驱动系统.Kurumaya等[2]研制出一种结构更紧凑且轻量化的细径气动肌纤维(PMF),由弹性橡胶内管和外编织套管构成.当向气动肌纤维内通入一定气体时,橡胶内管在气压的作用下发生变形,引起外编织套管的径向膨胀与轴向缩短,进而使得气动肌纤维收缩并产生收缩力.气动肌纤维具有柔性好、功耗小、响应迅速、驱动能量密度高等特点,驱动力可达27~29 N[3].气动肌纤维束(PMFB)可模仿二头肌、三角肌、扁平肌等,实现类生物肌肉的形状或功能[4],在微小型仿生机器人、微小型医用机器人、精密医疗等领域有很好的应用前景.
气动肌纤维的静态特性与相应的参数建模方法研究是实现其控制与应用的基础.国内外将气动肌纤维的静态特性数学模型划分为几何模型、现象模型、实验模型[5]三大类.2011年,比利时鲁汶大学将气动肌纤维用于驱动微型手术器械,并基于Colbrunn现象模型,考虑了橡胶内管的弹性变形以及橡胶内管与外编织套管之间的摩擦力,引入最小驱动力、长度损耗、气压损耗、橡胶内管弹性应变等附加参数,建立气动肌纤维静态特性改进模型[6].该模型的计算值与仿真值、实际测量值均具有良好的一致性.由于长度损耗、气压损耗等附加参数的具体数值不易确定,该模型难以具体应用.2014年,日本东京工业大学将气动肌纤维用于驱动肌肉骨骼机器人[4]及仿生六足机器人[7],气动肌纤维的静态特性采用Schulte几何模型[8].由于没有考虑橡胶内管的初始硬度和外编织套管与橡胶内管间的摩擦力,由Schulte模型获得的理论值与实际测量值相差较大,Schulte模型的最大收缩力约为7 N,而实际测量值可达13 N左右[2].2016年,日本东京工业大学采用Kagawa实验模型[9]计算气动肌纤维静态特性,并根据测量收缩力和收缩率的实验结果,通过最小二乘法拟合确定实验模型中的待定系数.Kagawa实验模型的计算值与实际测量值吻合得较好.2016年,为确定气动肌纤维束的收缩力,Kurumaya等[2]提出一种菱形模型,即气动肌纤维束充气向外呈放射状扩张,假设肌纤维束在二维平面上呈菱形,且气动肌纤维排列无间隙.由该菱形模型计算的收缩力及收缩率与气动肌纤维束的实际测量值较为一致.但菱形模型的收缩力会逐渐大于实际测量值,菱形模型的收缩率会逐渐小于实际测量值,且偏离程度会随着气压的增大而增大.总结目前国内外气动肌纤维静态特性的数学建模,由于忽略了端部变形、橡胶内管的初始硬度及外编织套管与橡胶内管间的摩擦作用,简单的几何模型和现象模型难以准确描述气动肌纤维的静态特性.基于几何模型或现象模型的改进模型虽能提高模型精度,但因引入了一些难以量化的参数增加了模型的复杂程度.实验模型利用实验数据拟合气动肌纤维的收缩力、收缩率与其内部气压之间的函数关系,可建立精度较高、表达式较简单的数学模型.为了更好地描述气动肌纤维的静态特性且便于控制器的设计与编程,建立气动肌纤维静态特性数学模型应基于工程实用化,在静态特性的精确程度与模型表达式的复杂程度之间找到一个合理的平衡点.
本文综合考虑气动肌纤维的端部变形、外编织套管纤维间的摩擦力、外套管与橡胶内管间的摩擦力、死区气压等对其静态特性的影响,开展气动肌纤维静态特性建模研究,提出一种气动肌纤维静态特性数学模型.该模型结合了几何模型与实验模型的优点,一方面基于几何约束,利用参数间的几何关系建立模型,另一方面利用实验数据拟合待定系数,解决气动肌纤维某些内部结构参数数值难以准确获取的问题.开展气动肌纤维等长实验、等张实验和等压实验,对比分析不同规格参数的气动肌纤维的静态特性,结合实验数据辨识出符合实际情况的气动肌纤维静态特性数学模型,并通过与实际测量值的对比验证所提模型的合理性.
1 气动肌纤维静态特性数学模型
所制作的气动肌纤维实物如图1所示,其结构参数如表1所示.
当气动肌纤维初始充气时,部分气体产生的压力用于抵消橡胶内管的初始硬度以及外编织套管与橡胶内管之间的间隙,气动肌纤维将不会收缩,也不会产生收缩力,用于抵消的这部分气压称为死区气压pd[10](结合实验结果,此处取pd=0.03 MPa),气动肌纤维的有效气压pe为

图1 PMF实物图Fig.1 Picture of PMF

表1 PMF的结构参数Tab.1 Structural parameters of PMF
pe=p-pd
(1)
式中:p为输入气压.
气动肌纤维的充气状态及几何参数关系分别如图2和3所示.其中;α0,r0,l0分别为气动肌纤维的初始编织角、初始半径、初始长度;α,r,l分别为气动肌纤维的工作编织角、工作半径、工作长度;N为外编织套管编织纤维缠绕圈数;lb为外编织套管编织纤维长度,由于编织纤维无弹性,lb保持恒定不变.计算气动肌肉或气动肌纤维的收缩力时,工作半径r通常取肌肉或肌纤维外编织套管的半径.由于McKibben型气动肌肉的管壁较厚,通常达到3 mm以上,所以肌肉壁厚对其收缩力的影响不能忽略,国内外关于气动肌肉的建模中也考虑了壁厚的影响[11].本文所分析的气动肌纤维的橡胶内管壁厚初始值仅为0.36 mm,编织纤维直径仅为0.16 mm,当输入气压突破死区气压时,橡胶内管的壁厚因肌纤维膨胀减小至不到0.10 mm.进行收缩力计算时,壁厚对收缩力的影响较小,故本文不考虑肌纤维壁厚对收缩力的影响.

图2 PMF的充气状态示意图Fig.2 Diagram of inflation status of PMF
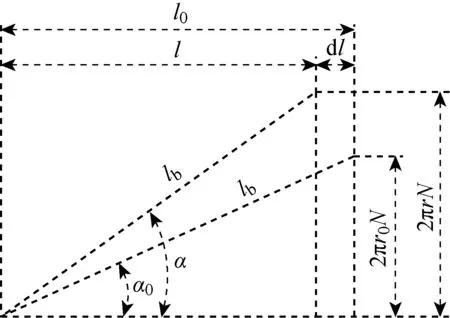
图3 PMF的几何参数关系示意图Fig.3 Diagram of geometric parameters of PMF
当p>pd时,气动肌纤维的有效输入功Win可表示为
dWin=pedV
(2)
式中:V为气动肌纤维的理想膨胀体积.理想状态下,气动肌纤维的输出功Wout可表示为
dWout=-Fdl
(3)
式中:F为气动肌纤维的收缩力.由能量守恒定律建立气动肌纤维理想静态特性数学模型[12-13],则有:
由几何关系计算可得:
(6)
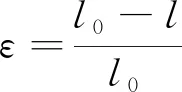
由于端部约束,气动肌纤维的实际膨胀体积小于理想膨胀体积,导致收缩力小于理想值.放大端部约束部分,橡胶内管膨胀与外编织套管圆柱体部分相切,如图4所示.
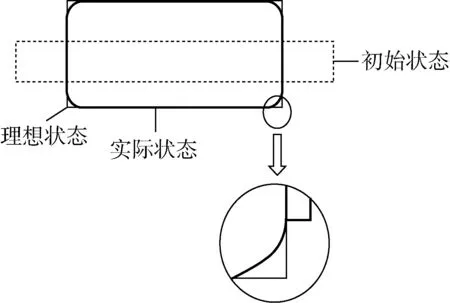
图4 PMF端部变形示意图Fig.4 Diagram of end deformation of PMF

图5 端部变形几何关系示意图Fig.5 Diagram of geometry of end deformation
气动肌纤维端部变形几何关系如图5所示.其中:rs为气动肌纤维实际膨胀情况下橡胶内管与外编织套管相切圆弧的半径,与其他几何参数的关系可表示为
rssinα=(r-r0)/(2sinα)
(7)
由气动肌纤维端部变形的几何关系,可计算理想圆柱形端部体积VL(两个端部),则有
(8)
实际端部体积Vs可表示为
(9)
由式(5)、(7)~(9)可得
(10)
(11)
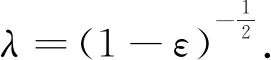
气动肌纤维充气过程中所产生的摩擦力主要包括外编织套管纤维间的摩擦力以及外套管与橡胶内管间的摩擦力.当输入气压较小时,橡胶内管尚未完全膨胀,与外套管间的接触面积较少,此时摩擦力以外编织套管纤维间的摩擦力为主.随着气压的增大,外套管工作编织角逐渐增大,纤维间的摩擦力逐渐减小,该特性与e指数函数的线性相似[14],引入修正系数qpe,当输入气压达到一定程度时(结合实验结果,以有效气压0.20 MPa为界),橡胶内管完全膨胀,外套管工作编织角增大,纤维间接触较少,此时摩擦力以外套管与橡胶内管间的摩擦力为主,引入修正系数kε.
式中:aε,bε,cε为待定系数,可通过最小二乘法拟合确定.
(14)
式中:a1~a3,b1~b3,c1~c3为待定系数,可通过最小二乘法拟合确定.
综上,考虑气动肌纤维的端部变形,外编织套管纤维间的摩擦力,外套管与橡胶内管间的摩擦力以及死区气压,气动肌纤维静态特性数学模型为
F(pe,ε)=
(15)
pe<0.20 MPa
F(pe,ε)=
(16)
pe≥0.20 MPa
2 气动肌纤维静态特性实验
2.1 气动肌纤维制作
将单根气动肌纤维及气动肌纤维束的一端固定在带有进气口的密封帽内,另一端通过绳结密封,两端均粘结由Dyneema纤维制的肌腱,制作单根肌纤维(SPMF)及肌纤维束如图6所示,其规格参数如表2所示,其中n为肌纤维数量.

图6 SPMF与PMFB示意图Fig.6 Diagram of SPMF and PMFB

表2 SPMF与PMFB规格参数Tab.2 Specifications of SPMF and PMFB
2.2 实验系统
实验系统如图7所示,实验平台如图8所示.所使用的硬件主要有单根肌纤维及肌纤维束、高精密x轴位移台、运动控制器、力传感器、比例阀、空气压缩机及PC上位机.由运动控制器控制位移台沿轴向移动,改变气动肌纤维的工作长度进而间接改变气动肌纤维的收缩率,由电气比例阀控制气动肌纤维的输入气压,由力传感器测量气动肌纤维的收缩力.利用该实验平台,开展气动肌纤维静态特性等长实验、等张实验和等压实验.
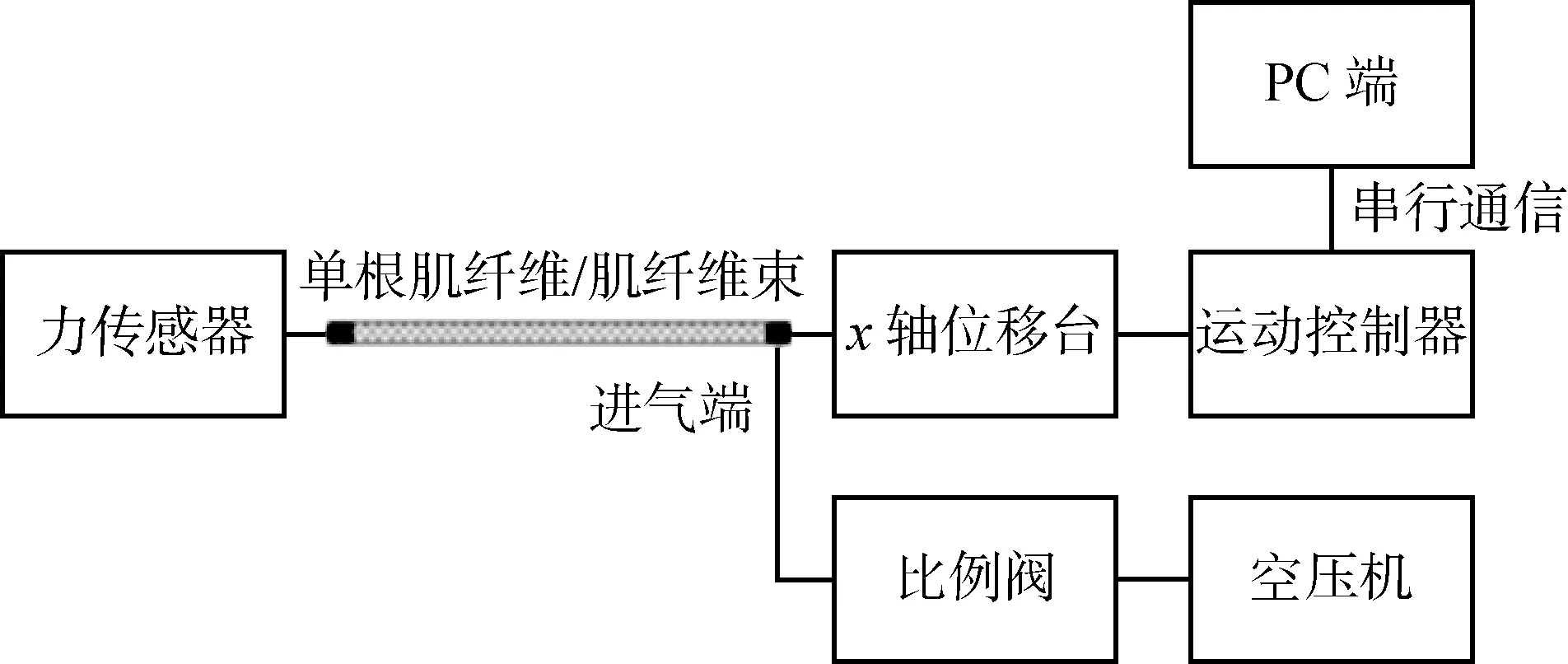
图7 实验系统图Fig.7 Diagram of experimental system
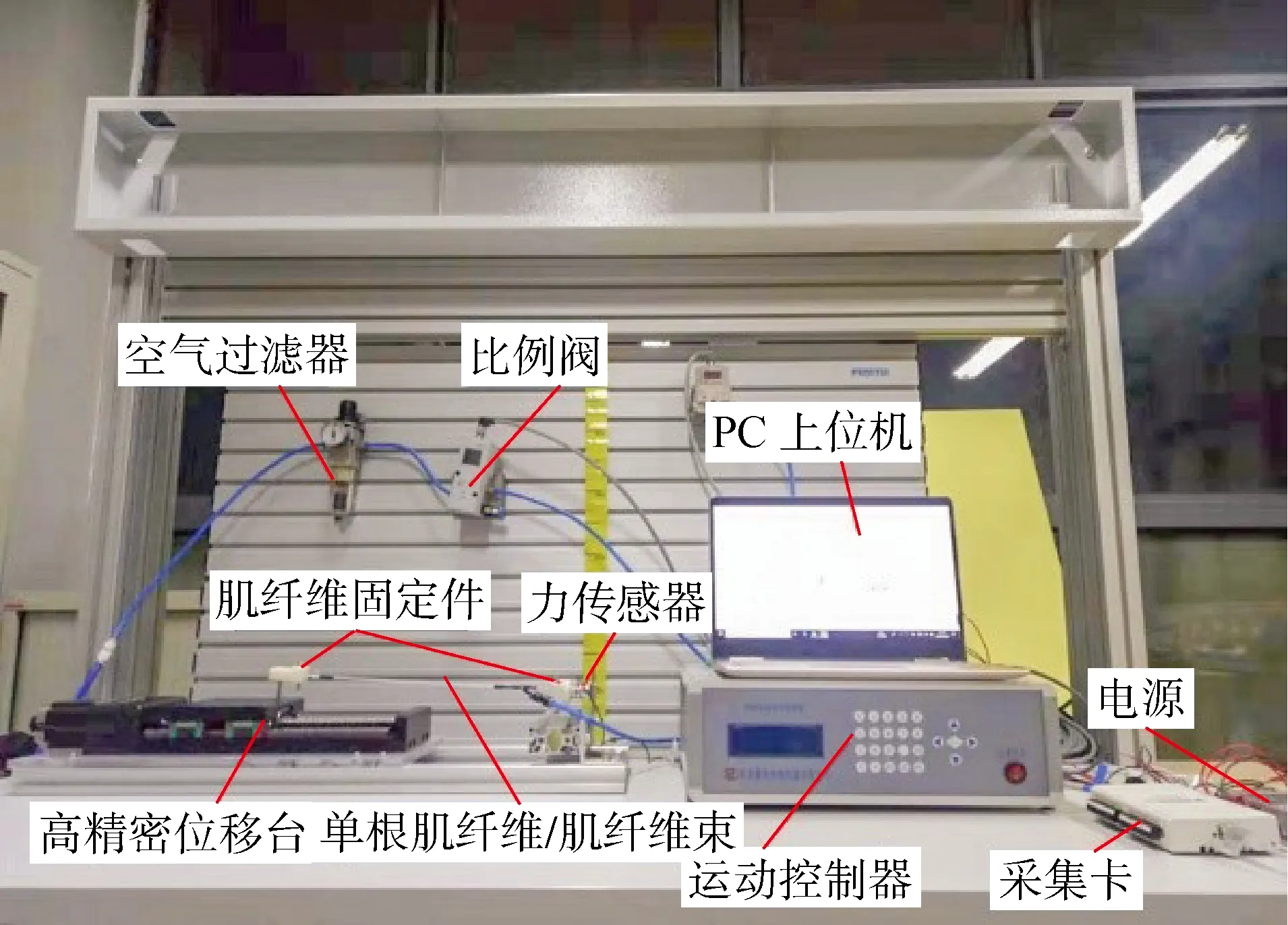
图8 实验平台Fig.8 Experimental platform
2.3 等长实验
保持单根肌纤维的收缩率为0,即保持单根肌纤维的初始长度不变,输入气压以0~0.50 MPa递增,分别测量初始长度为120、200、300 mm时,F随p的变化曲线,如图9所示.
由于橡胶内管的初始硬度及外编织套管与橡胶内管之间的摩擦,气动肌纤维和生物肌肉一样具有一定的迟滞特性[15], 经过多次实验,气动肌纤维的迟滞特性趋于稳定.
保持肌纤维束的收缩率为0,即保持肌纤维束的初始长度不变,输入气压以0~0.35 MPa递增,测量初始长度为120 mm的肌纤维束(肌纤维数分别为6、8、10)的收缩力FB随p的变化曲线,如图10所示.
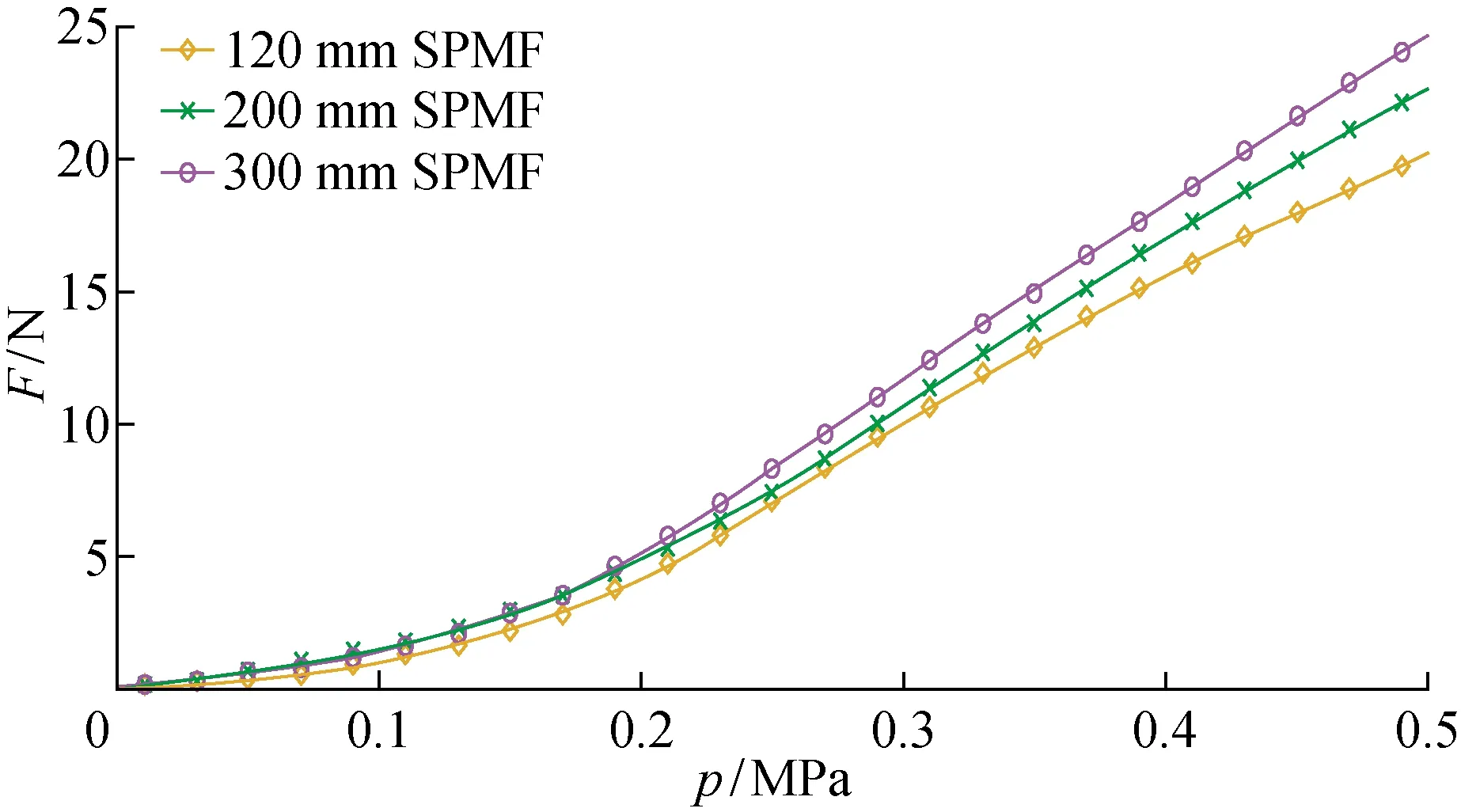
图9 不同初始长度下,SPMF的F随p的变化Fig.9 F of SPMF versus p at different initial lengths
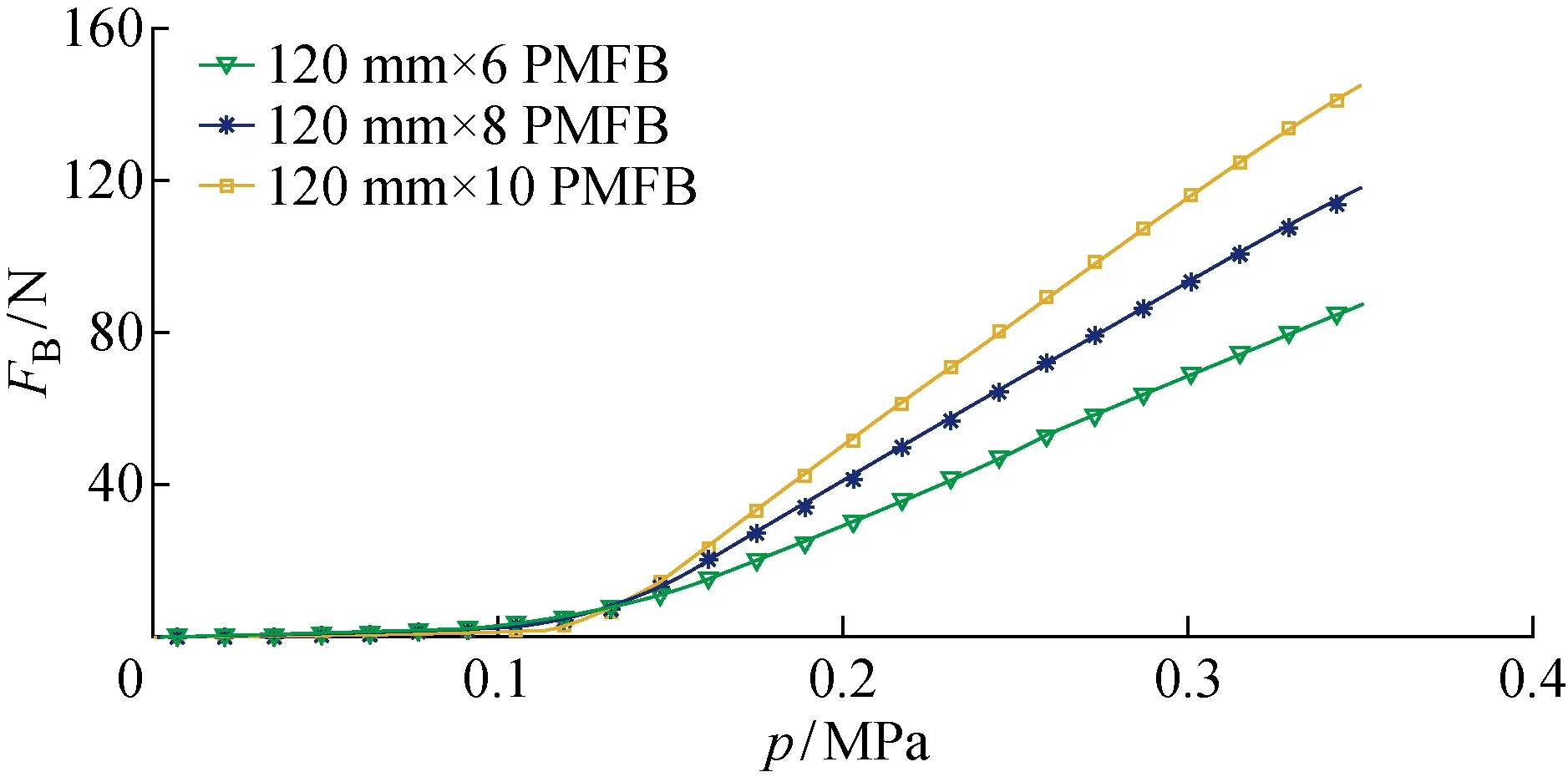
图10 不同肌纤维数下,FB随p的变化Fig.10 FB versus p at different numbers of muscle fibers
由图9~10可以看出,气动肌纤维束的收缩力不是简单的线性叠加.由于气动肌纤维的径向膨胀受限以及气动肌纤维外套管间的摩擦力,气动肌纤维束的收缩力除了与气压、收缩率有关之外,还与肌纤维数存在一定的非线性关系.
2.4 等张实验
保持单根肌纤维与肌纤维束的收缩力为0,输入气压以0~0.30 MPa递增,分别测量初始长度为120 mm的单根肌纤维、初始长度为120 mm的肌纤维数分别为6、8、10的肌纤维束的ε随p的变化曲线,如图11所示.

图11 不同肌纤维数的PMFB及SPMF的ε随p的变化Fig.11 ε of different numbers of PMFB and SPMF versus p
由图11可以看出,气动肌纤维间的摩擦导致橡胶内管的温度升高、硬度降低,肌纤维束的收缩率在一定气压范围内略大于单根肌纤维的收缩率,但气动肌纤维收缩到一定程度后就不能再收缩了,最大收缩率取决于其结构参数,如外套管的初始编织角、橡胶内管的弹性模量等,实验用气动肌纤维的最大收缩率约为29%.
2.5 等压实验
保持输入气压不变,分别测得不同气压下的单根肌纤维及肌纤维束的等压特性曲线,记录大量实验数据,用于辨识气动肌纤维静态特性数学模型.电气比例阀控制输入气压,运动控制器控制高精密位移台实现气动肌纤维的拉伸与收缩,以间接改变气动肌纤维的收缩率.设定气动肌纤维的匀速拉伸/收缩速度为0.2 mm/s,即每5 s拉伸/收缩1 mm,待收缩力保持稳定后采集气动肌纤维的收缩力.
初始长度为120 mm的单根肌纤维,输入气压p的取值范围为0.05~0.30 MPa,气压变化增量Δp为0.05 MPa,实验测得的6组等压特性曲线如图12所示.

图12 初始长度为120 mm的SPMF等压特性曲线Fig.12 Isobaric characteristic curves of SPMF at an initial length of 120 mm
实验中发现,由于气动肌纤维的阻尼特性,当以一定的速度对气动肌纤维进行充气时,气动肌纤维会产生一定的附加力,稳定一段时间后附加力消失.气动肌纤维的阻尼特性在实际应用中能起到吸收能量和缓冲减震的作用.
初始长度为120 mm,肌纤维数为6、8、10的肌纤维束,p的取值范围为0.05~0.30 MPa,Δp为0.05 MPa,实验测得的18组等压特性曲线如图13~15所示.
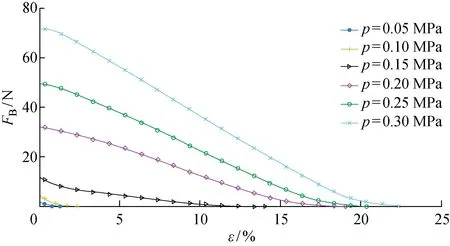
图13 120 mm×6 PMFB的等压特性曲线Fig.13 Isobaric characteristic curves of 120 mm×6 PMFB

图14 120 mm×8 PMFB的等压特性曲线Fig.14 Isobaric characteristic curves of 120 mm×8 PMFB

图15 120 mm×10 PMFB的等压特性曲线Fig.15 Isobaric characteristic curves of 120 mm×10 PMFB
由图13~15可以看出,每组等压曲线中气动肌纤维束的收缩力随收缩率的增大而减小,近似于弹簧的刚度特性.然而弹簧的刚度通常是恒定的,取决于其材料特性和几何结构[16],而气动肌纤维束的刚度是一个可变参数,除了上述因素还与pe和n有关.在气动肌纤维束的材料、几何结构确定的情况下,其可变刚度特性可以描述为
(17)
3 气动肌纤维静态特性数学模型识别
3.1 气动肌纤维静态特性数学模型识别
气动肌纤维静态特性数学模型如式(15)~(16)所示.当pe<0.20 MPa时,采用MATLAB数据拟合工具箱cftool对每组数千个等压实验数据进行拟合,最终确定待定系数aε=4.716,bε=-2.728,cε=-0.779.
当气动肌纤维内的pe≥0.20 MPa时,首先对不同气压的等压曲线分别进行拟合,以得到k(ε)与ε的映射关系;在此基础上,再对α(pe),β(pe),γ(pe)的相关系数进行拟合,拟合结果为a1=5.547,b1=-2.470,c1=2 329,a2=-3.971,b2=1.764,c2=-0.198,a3=-5.548,b3=2.471,c3=-2 329,进而获得完整的气动肌纤维静态特性数学模型.
3.2 气动肌纤维束静态特性数学模型识别
基于上述分析,气动肌纤维束的收缩力FB除了与pe和ε相关之外,还与n成非线性关系.将相同气压(0.30 MPa)、相同初始长度(120 mm),肌纤维数分别为6、8、10的肌纤维束的等压特性曲线进行对比,如图16所示.

图16 在初始长度和气压相同的情况下,不同肌纤维数的PMFB的等压特性曲线Fig.16 Isobaric characteristic curves of PMFB with different numbers of muscle fibers at the same air pressure and initial length
根据FB与n的非线性关系,提出一种气动肌纤维束静态特性数学模型,可表示为
FB(n)=τF2+φF+ω
(18)
τ=d1n2+e1n+f1
φ=d2n2+e2n+f2
ω=d3n2+e3n+f3
式中:τ,φ,ω,d1~d3,e1~e3,f1~f3均为多项式待定系数,采用最小二乘法可确定其具体数值.此处取值如下:
p=0.30 MPa,pe=0.27 MPa,F=F(0.27,ε)
采用MATLAB数据拟合工具箱cftool对每组数千个气动肌纤维束等压实验数据进行拟合,拟合过程分为两个步骤.
(1) 对不同n的等压曲线分别进行拟合,获得FB与F的映射关系为FB=FB(F),拟合结果如表3所示.
(2) 在(1)的基础上,针对τ,φ,ω的相关系数对n进行拟合,拟合结果如表4所示.

表3 不同肌纤维数下的多项式系数拟合结果

表4 τ,φ,ω的相关系数拟合结果
因此,气动肌纤维束的静态特性数学模型可表示为
FB(n)=
(0.009 2n2-0.185 4n+0.639 5)F2+
(-0.191n2+4.418n-12.54)F+
(-0.273 1n2+4.651n-17.49)
(19)
4 模型计算值与实验值对比
将气动肌纤维模型的计算值与目前国内外大多采用的Schulte模型的计算值、等压实验测量值进行对比,如图17所示.
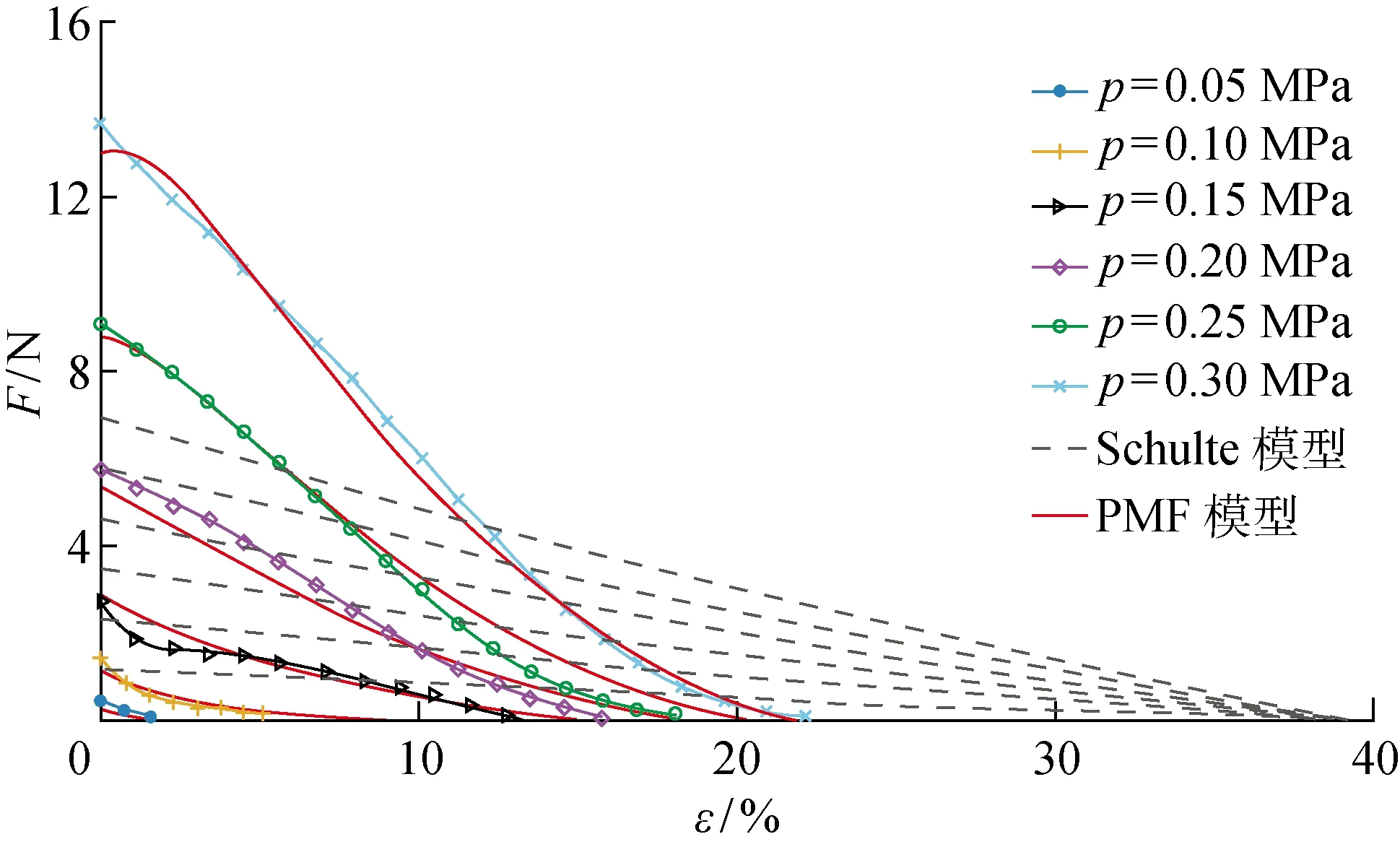
图17 PMF模型计算值与Schulte模型计算值及等压实验测量值对比Fig.17 Comparison of calculated values of PFM model and Schulte model and measured values of isobaric experiment
由图17可知,与Schulte经典模型对比,所建立的气动肌纤维模型综合考虑气动肌纤维的端部变形、外编织套管纤维间的摩擦力、外套管与橡胶内管间的摩擦力以及死区气压等因素对气动肌纤维静态特性的影响,可看出该模型计算值与实验值具有较好的一致性.
将输入气压为0.30 MPa,初始长度为120 mm,肌纤维数分别为6、8、10的气动肌纤维束模型与实验值对比,如图18所示.由图18可知,两者吻合度较高.
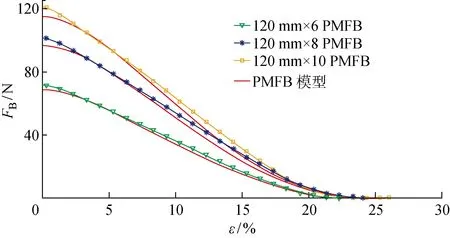
图18 初始长度相同,肌纤维数不同的PMFB模型计算值与实验测量值对比Fig.18 Comparison of calculated values and measured values of PMFB model at different numbers of muscle fibers and the same initial length
5 结语
本文综合考虑气动肌纤维的端部变形、外编织套管纤维间的摩擦力、外套管与橡胶内管间的摩擦力以及死区气压等对气动肌纤维静态特性的影响,提出的气动肌纤维静态特性数学模型弥补了几何模型、实验模型的不足.一方面基于几何约束,利用参数间的几何关系建立数学模型,另一方面利用实验数据拟合待定系数,解决了气动肌纤维某些内部结构参数的数值难以准确获取的问题.开展气动肌纤维静态特性等长实验、等张实验、等压实验研究,对比分析不同结构参数的气动肌纤维的静态特性.由大量实验数据辨识获得符合实际情况的气动肌纤维静态特性数学模型,与实验值对比验证了该气动肌纤维静态特性数学模型的合理性.
