基于可靠性理论的工程车辆结构强度设计

马智文，郭 超

（贵州交通职业技术学院，贵州 贵阳 550000）

0 引言

据统计，工程车辆的结构件重量占整机重量的50%～70%。在保证工程车辆结构强度的基础上，减轻车身的重量，对降低成本、提高作业效率、增加燃油经济性有重要的作用。

传统结构强度设计的核心观点是：材料的强度值大于或者等于载荷产生的应力[1]。即：

一般认为，满足上述条件，所设计的结构强度是可靠的。

传统的结构强度设计方法认为材料的强度和载荷应力均为恒定值。然而随着时间的推移，由于材料在动载荷、腐蚀、磨损、疲劳载荷的长期作用下，材料强度会逐渐衰减，同时外加载荷随着工况的不同，其产生的应力大小也不断地发生着变化。因此，该设计存在如下缺陷：1）使用初期，材料强度大于应力，但随着时间的推移，材料强度存在小于应力的可能，即随着时间的变化结构变得不可靠，而设计人员却无法预知；2）由于设计时外加载荷被假定为恒定值，在极端工况下，存在应力大于结构强度，从而结构发生破坏的情况。

本文在前人工作的基础上，基于可靠性理论，结合工程实践系统性地阐述了工程车辆结构可靠性设计的方法。

1 工程车辆结构强度设计

1.1 可靠性理论下的结构设计

可靠性理论认为零件强度会受到外加载荷、磨损、加工质量、润滑状态等因素的影响，由于这些影响因素的状态是随机变化的，因此强度为随机变量[2]。同理，应力在载荷工况、零件尺寸、工作温度等因素的影响下也为随机变量。

用f(x)表示零件强度，用g(x)表示零件应力，则某一时刻下，零件的应力和强度的关系如图1所示：

图1 应力-强度干涉图

通常零件的强度是高于其应力的，但由于强度与应力的随机性，使得应力-强度两概率密度函数曲线在一定条件下可能存在相交的区域，这一区域被称为干涉区，在该区域内零件可能出现破坏，同时干涉区域的面积即为不可靠度。

从时间角度讲，零件使用初期，强度分布与应力分布不存在交集，但随着时间的变化，强度慢慢减小，最后出现了干涉区域，如图2所示。因此，干涉区域面积的大小及其变化是可靠性设计重点关注的核心，是量化可靠度的重要内容。

图2 应力-强度干涉图随时间的变化情况

综上，基于可靠性理论的结构强度设计的主要内容为：确定基于实际工况下的应力和零件强度分布函数；根据设计要求，量化零件的可靠度；进行零件结构参数的确定。

1.2 基于可靠性理论的结构强度设计过程

1.2.1 零件可靠度的确定

工程车辆结构可靠性设计的起点是确定可靠度，即是确定在额定工作时间下的可靠度。可靠度的具体确定主要是根据机械产品的市场信息反馈或者客户的具体需求。一般而言，主要根据产品故障引发的危险性程度及经济性后果来确定。破坏后，造成的危险性较高、经济损失较大的零部件，其可靠性等级往往需要较高。产品可靠性水平等级与可靠度的关系如表1所示。对于工程车辆而言，关键零部件一般选择4级，特殊结构选用5级。

表1 可靠性等级与可靠度关系

1.2.2 结构可靠性设计的具体流程

在工程车辆的实际设计过程中，一般采用如下的设计流程，如图3所示：根据确定好的应力概率分布和强度概率分布，建立应力-强度的干涉模型；然后建立基于可靠度的应力、强度关系式；最后确定零件结构参数。

图3 结构强度可靠性设计流程图

1.2.3 应力（强度）概率分布的确定

应力是计算零件截面上载荷与截面几何尺寸的函数，强度是关于零件材料性能和几何尺寸的函数，因此求取应力（强度）概率分布实际上需要先求取载荷、几何尺寸以及零件材料性能的概率分布；然后再根据这三者的概率分布，计算出应力（强度）的概率分布。

概率分布确定过程中的数据来源主要有：1）产品使用或维修过程中的统计资料；2）可靠性试验产生的数据；3）可靠性解析式计算或预测的数据。统计或试验数据一般需要经过统计和分析才能进行使用。

载荷概率分布的计算要求进行实测，即对载荷-时间历程进行记录、计算，再根据数理统计，确定分布类型和建立数学模型。零件材料性能概率分布一般要求对材料进行一定数量的试验，然后根据试验数据，确定概率分布。由于金属材料的力学性能相对稳定且工艺已经流程化，因此金属材料的概率分布可以通过已有的金属材料手册数据进行近似计算；对于新材料，由于对其研究和认识不充分，必须经过试验、统计得出概率分布。几何尺寸受到加工设备精度、量具精度以及人员的操作水平的影响，其概率分布可通过实际测量计算得到，大量统计表明，几何尺寸一般呈现正态分布[3]。

确定载荷概率分布、几何尺寸概率分布、零件材料性能概率分布后，可通过各参数之间的函数关系求取应力（强度）的概率分布。通过对大量文献的综合分析，目前确定应力、强度分布的方式主要有以下几种：

1）代数法[4]。设影响零部件应力或强度的参数为X1，X2，……，Xn，且它们相互独立且服从正态分布，则可根据应力（强度）与参数的函数关系，把它们综合成仅含单一随机变量的应力或强度表达函数，按照正态分布函数的运算可求出其分布。显然，该方法的应用范围主要针对影响参数为正态分布的情况。

2）矩阵法[4]。当应力或强度函数f(x)比较复杂时，其数学期望和方差将很难获取，此时采用泰勒展开式，计算展开式的数学期望及方差。该方法虽然得到的是近似解，但是求解容易，精度也足够高。

3）Monte-carlo 法[5]。影响零部件应力或强度的参数为X1，X2，……，Xn，可能并非属于同一分布，此时应力或强度分布函数f(x)将很难解析或者根本就无法解析。Monte-carlo法可以用于解决此问题，其主要的策略为：对于每一个参数Xi，产生若干符合其分布的点，代入公式就得到若干符合Y分布的点，从而模拟出Y 的分布。该方法需要借助计算机，以统计抽样理论为基础，是目前解决工程技术问题近似解的一个数值计算方法，广泛应用于工程中。

1.2.4 基于可靠度的应力、强度关系式的建立

令f(s)为应力分布的概率密度函数，g(δ)为强度分布的概率密度函数，如图4所示。

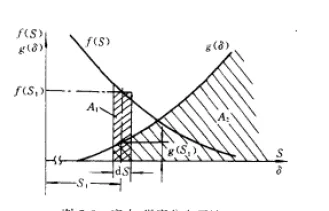
图4 应力-强度分布干涉

应力值S1落于宽度为dS的小区间的概率为：

强度δ大于应力S1的概率为：

由于强度分布和应力分布属于两个独立随机事件，因此，在dS的小区间内，不会出现失效的概率（即可靠概率）为：

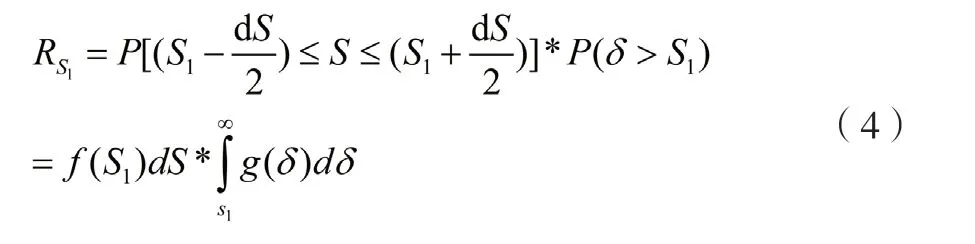
由于S1为随机选取的区间，因此在整个定义域内，可通过对RS1进行积分，即可得到整个零件的可靠度。

该方程即为基于可靠度的应力强度关系式，其中可靠度R 在零件设计前便已经确定，应力密度函数f(s)和强度密度函数g(δ)也已经确定，因此求解该方程便可得到整个零件的设计参数。

1.2.5 基于正态分布的可靠性结构设计

根据文献和实践应用，结构的强度分布和应力分布服从正态分布的情况较为常见。因此本文结合强度分布和应力分布均服从正态分布情况下，对结合参数的设计进行说明。

应力和强度服从正态分布时，其密度函数为：

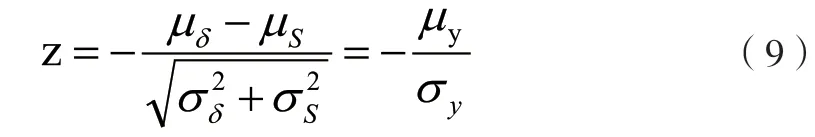
当y为+∞时，z也为+∞，故可靠度R可写为：

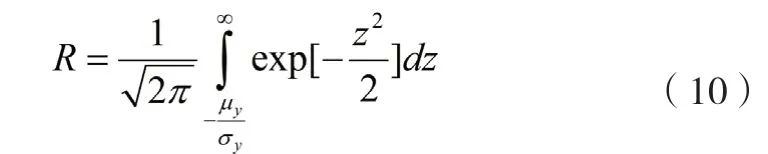
由于随机变量z 属于正态分布，因此，可靠性公式可写为分布函数的形式：

其中，zR=-z=，称为可靠性指数。

可见，对于应力分布和强度分布属于正态分布的情况，可通过应力和强度的均值和标准差及可靠度求取结构的设计参数。

1.2.6 工程实践中的数据处理

综上所述，求取应力（强度）概率分布前，需确定载荷、几何尺寸以及材料性能的分布。确定分布的最佳方式是通过实验或者统计数据进行统计，然而由于企业往往很难进行大规模的基础性实验，因此在进行结构可靠性设计时，最佳的做法是充分利用好以往的数据。

1）求取载荷概率分布的常见做法：如果企业以往有相关的载荷统计数据，可进行一定的处理后直接使用；若无相关数据，则必须进行载荷-时间历程的试验。鉴于载荷分布的准确性直接影响应力和强度分布的准确性，因此务必重视该项试验。

2）求取几何尺寸分布的常见做法[2，6-7]：文献显示，几何尺寸的偏差一般服从正态分布，因此批量加工零部件的几何尺寸可认为符合正态分布，一般按照“3倍标准差原则”进行参数的确定。

3）求取材料性能分布的常见做法[2，6-7]：相关文献及书籍显示，金属材料的抗拉强度、屈服强度一般能较好地符合或近似符合正态分布，大部分材料的疲劳强度服从正态分布或对数正态分布，部分材料的疲劳强度服从威布尔分布。因此在具体使用过程中，可翻阅相关的资料，确定材料性能的分布类型后，再通过材料手册进行计算。

2 结语

工程车辆的结构强度可靠性设计需要大量的试验数据，试验数据越丰富，所求解的概率分布就越准确，但是在实践过程中，由于条件的限制部分数据往往采用近似的方式进行处理。从理论上讲，对设计的精度有一定的影响。为确保结构强度可靠性设计的效果，应该做好产品使用、维修过程中的数据采集和记录，以便在新产品的设计中进行优化。