基于自适应旋转角度的CORDIC 算法的设计与仿真

2021-06-01

数字技术与应用 2021年4期

(南京恩瑞特实业有限公司,江苏南京 211100)

0 引言

CORDIC(Coordinated Rotation Digital Computer)算法只有移位和加减运算,便于在FPGA等硬件平台上实现复杂的三角函数、双曲函数、指数函数和复数求模等计算,广泛的应用于数字上下变频、波形产生、数字鉴相、快速傅里叶变换[1-2]等方面。

传统的CORDIC算法旋转的角度固定,通常需要较多的迭代次数才能实现较高的运算精度。近年来,大量学者在提高CORDIC算法运算精度、增加角度覆盖范围、减少迭代次数、降低资源消耗方面进行了大量的研究。文献[3]结合区间折叠技术和双步旋转策略,减少了迭代次数且具有较高的运算精度,但时延很大。文献[4]采用单向固定旋转方式降低了算法的延迟时间和资源消耗,但该算法运算精度较低。文献[5]提出将多种技术综合起来,可以有效降低输出时延,但硬件实现较为复杂。文献[6]提出单向最优迭代的CORDIC算法,具有实时性强、资源消耗少的优点,但该方法迭代结束时间判定复杂,硬件实现困难,难以应用于高速系统。

在相同迭代次数下,CORDIC算法运算精度与算法可以遍历的角度个数密切相关,但上述算法每一级的旋转角度固定,算法可遍历的角度个数较少。通常采用增加迭代次数、数据长度、存储深度等方法来提高运算精度,代价是延迟时间的增加以及硬件资源的消耗。本文提出了一种自适应旋转角度的CORDIC算法,根据输入的角度自适应选择每一级迭代的旋转角度,不需要消耗大量存储资源,具有收敛速度快,延迟时间短、可遍历角度个数多、运算精度高的优点。

1 CORDIC算法

1.1 传统的CORDIC算法

在直角坐标平面上将点(x1,y1)逆时针旋转θ角度到点(x2,y2)的标准方法如式(1)所示:

CORDIC方法的核心是旋转角度θ满足tanθi=2-i。每次旋转的表达式如式(2)所示:

式中z表示每次迭代累加的旋转角度,符号di=±1是判决算子,决定旋转方向。

CORDIC算法的旋转角度限定在第一象限,且每次旋转都会影响最终要旋转的累积角度,因此仅在-99.7°≤θ≤99.7°的范围内的任意角度可以旋转。为了保证旋转前后幅度不变,对CORDIC输出的数据乘以一个系数A,如式(3)所示:

传统的CORDIC算法实现较为简单,但每次旋转的角度固定,要实现较高精度的计算,需要多级流水线结构,多级流水线结构延迟大且会增加硬件成本。

1.2 改进的CORDIC算法

本文在传统的CORDIC基础上提出改进的CORDIC算法。根据输入的角度自适应选择每次旋转的最优角度,仅需要消耗少量存储资源且在旋转次数较少的情况下即可实现较高精度的正余弦值计算,延迟时间短,实时性强。改进的五级旋转CORDIC算法结构如图1所示。

建立两个数组CS、XX,CS存储角度值,XX存储对应的余弦值。根据每一级旋转的剩余角度从CS与XX中选择最优的旋转角度与余弦值补偿因子。角度表达式为:

式(4)中μ(i)∈{1,-1,0}决定第i次旋转的方向,1表示逆时针旋转;-1表示顺时针旋转;0表示旋转已经达到最小精度值,剩余角度已经为0;ε为误差值。a(s(i))表示第i次旋转的度数,s(i)∈{0,1,2,…,n-1},i∈{1,2,3,…n-1},n为数组的长度,为便于计算机实现,令:

综上可得迭代方程如式(6)为:

每一次旋转中,比较剩余角度的绝对值与数组CS 中的角度判断出此次旋转的最优角度值,并记录其余弦值,将每次旋转记录的余弦值相乘得到补偿因子Pn。

改进后的CORDIC算法有以下优点:

(1)对于某些特殊角度如:45°,arctan(2-1),…只需要一次选转即可使误差为零,传统算法旋转多次后仍有较大误差;

(2)量化位数、流水线级数相同时,改进后的CORDIC算法,跳过某些旋转,可以达到的精度远高于传统算法;

(3)只需要4级迭代,就可覆盖角度-π～π。

2 算法仿真与比较

本文将提出的自适应旋转角度CORDIC算法与传统的基于固定旋转角度的CORDIC算法在计算精度、遍历角度个数、收敛速度以及计算量方面进行仿真对比。

图1 改进CORDIC 算法五级流水线结构Fig.1 Improved five-stage pipeline structure of CORDIC algorithm

首先对0-360°范围的角度分别采用传统CORDIC算法与改进的CORDIC算法计算正弦值,计算误差如图2所示。仿真过程中角度从0°变化到360°,步进1°,角度量化为12位,幅度量化为12位,两种算法均采用五级迭代。从图2可以看出,相同的迭代次数下,改进的CORDIC算法计算的正弦值更接近标准的正弦值。

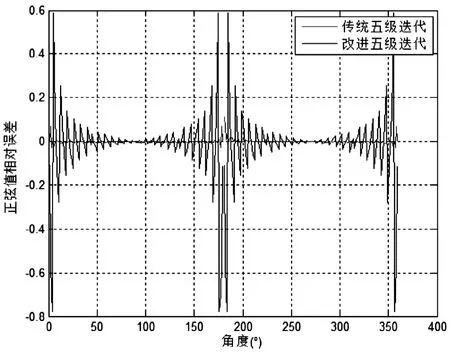
图2 0°-360°正弦值误差比较Fig.2 0°-360° sine value error comparison

仿真中分别对两种算法迭代3-7 次时能够遍历的角度个数进行比较,如图3所示。从图3可以看出两种算法可以遍历的角度个数均随着迭代次数的增加而增加,迭代次数相同时改进的CORDIC 算法可以遍历的角度个数明显比传统算法多。改进的CORDIC算法每一级旋转可以选择更多角度,因此可以准确计算的角度个数增加,从而提高了CORDIC算法计算正余弦值的精度。

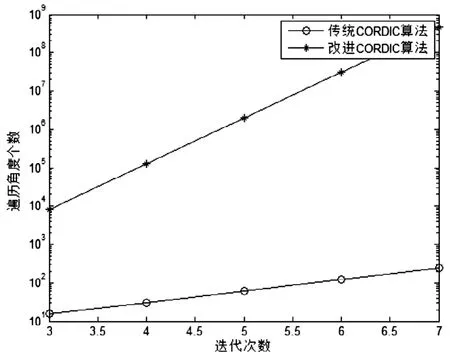
图3 两种算法角度遍历比较Fig.3 Comparison of angle traversal between two algorithms

图4为两种算法收敛速度的仿真比较。随机产生0-90°的输入角度,比较传统算法与改进算法每一级迭代后的剩余角度,重复实验1000次。从图4可以看出两种算法剩余角度均随着迭代次数的增加而趋近0,但是改进后的算法收敛速度更快。

图4 两种算法收敛速度比较Fig.4 Comparison of the convergence speed of the two algorithms

传统的CORDIC算法每次迭代过程需要进行一次角度判断、两次移位和三次加减法运算。改进的CO RDI C算法每次迭代过程需要进行一次角度比较、一次角度判断、两次移位和三次加减法运算。改进的算法比传统的算法多一次角度的比较,具体的运算量由角度数组CS 的大小决定。改进的CORDIC算法以略复杂的角度比较换取更少的迭代次数与更高的精度。