基于超像素的粘连谷粒分割算法

(南京理工大学计算机科学与工程学院,江苏南京 210094)

0 引言

影响水稻产量的重要因素有稻谷形状,该因素受基因控制,谷粒形态已成为水稻品种评价和选种的主要衡量指标之一。最初,是通过工作人员利用长度测量设备来得到谷粒形态,但该方法耗时耗力。接着,出现了谷粒测量机器,但在测量之前,也需要工作人员对谷粒进行一定的预处理,仍需要耗费人力。随着图像处理技术的快速发展,目前基于图像的谷粒形态测量方法已被广泛使用[1]。在测量谷粒形态之前,首先需要将谷粒从图像中准确分割出来。常用的分割方法包括OTSU、直方图阈值法以及分水岭分割等[2]。由于谷粒间存在不同程度的粘连,如果采用分水岭分割,则会造成欠分割。另外,谷粒图像受不同光照和背景影响,如果采用OTSU 和直方图阈值法分割,则会造成分割错误。针对上述问题,本文提出了基于超像素的粘连谷粒分割算法。

1 基于超像素的粘连谷粒分割算法

1.1 超像素初步分割

超像素分割,就是把一些邻近的,并且属性相近的像素聚类成一个大的“像素”,称之为超像素。这里像素的属性,包括像素的亮度,颜色值,纹理等因素。对图像作超像素分割的优点是,可以降低处理复杂度,同时也可以去除噪声点。

由于单个像素的RGB值易受噪声影响,为提高分割准确率,本文采用SLIC(Simple Linear Iterative Clustering)超像素分割方法[3]对谷粒图像进行初步分割,将其分为一定大小的超像素。SLIC超像素分割算法如下:

(1)输入谷粒图像I,假定该图像中共包含N个像素,将图像从RGB空间转换到Lab空间。

(2)确定初始聚类中心。首先,输入超像素的数目M,则定义作为初始聚类中心之间的距离。按S在图像中确定M 个初始聚类中心,表示为Ci=(li,ai,bi,xi,yi),。

(3)调整初始聚类中心位置。如果初始聚类中心位于图像中梯度较大位置,则初始聚类中心相当于位于图像边缘,这会造成分割错误。因此,需要将初始聚类中心按其梯度值进行调整,将其移至梯度值较小的位置。例如,图1是对谷粒图像中的局部区域经放大后的效果,由于A点位于图像的边缘,我们不希望初始聚类中心位于A 点,而B点和C点位于图像中较为平稳的位置,这两个位置的梯度值都较小,可以将B 点和C 点作为初始聚类中心。

图1 初始聚类中心的不同位置Fig.1 The different position of initial clustering centers

(4)利用k-means算法[4],计算聚类中心邻域范围(2S×2S)内各像素到其之间的距离,并将像素归类到与其距离最近的初始聚类中心。

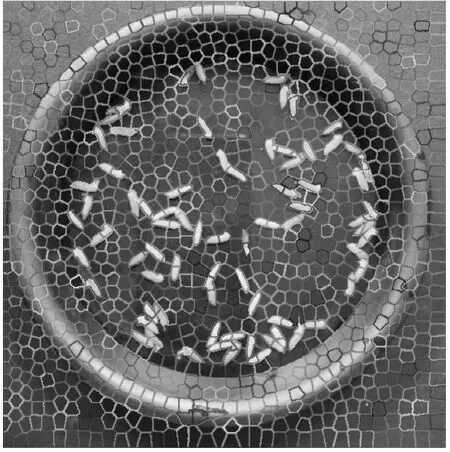
图2 SLIC 分割结果Fig.2 The segmentation result of SLIC

像素到聚类中心之间的距离定义为:

其中,i为第i个聚类中心,j是第j个像素点,Ns等于步长S,Nc为颜色分量的最大距离。

(5)迭代运算。对每个新得到的簇重新计算其聚类中心,当聚类中心不再变化,则聚类结束,输出聚类结果。

图2显示了利用SLIC超像素分割的结果,从图中可见,有的单个谷粒被分割为一个超像素,有的则被分割成多个超像素。接下来,需要对谷粒部分利用超像素分割结果进行进一步分割。

1.2 谷粒分割

谷粒的颜色是黄色,而黄色的特点是像素的红色,绿色和蓝色三个分量中,红色和绿色的值要大于蓝色,利用该特点,我们可以在超像素分割基础上对谷粒作进一步分割。

图3 四种算法的分割结果Fig.3 The segmentation results of four algorithms

表1 四种算法的分割准确率 (%)Tab.1 The segmentation accuracy of four algorithms (%)

假定谷粒图像的颜色用RGB空间表示,即图像中各像素表示为(R,G,B)三基色值,我们先将RGB空间变换到(R-B,G-B)空间,即像素点采用(rb,gb)两个数值表示。

接着,统计各超像素块中rb和gb分别大于阈值的像素的数目nrg,实验发现,谷粒中像素的rb要大于gb。本文将满足式(6)的像素统计进nrg中:

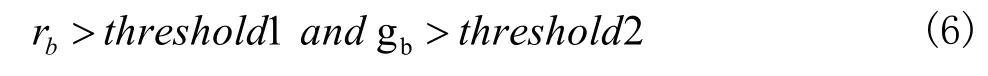
其中,threshold1和threshold2分别定义35和20。

得到nrg之后,计算各超像素的比值ratio:

其中,n为超像素块中像素的总数。

我们可以假定,当超像素为谷粒时,其中大部分像素应该满足式(6),即ratio值应该偏大,而当超像素为背景时,则其ratio值应该偏小。因此,我们将ratio值大于0.5的超像素作为谷粒,否则作为非谷粒。

2 实验结果

为验证本文算法的有效性,我们将本文算法与直方图阈值法,OTSU,以及分水岭分割法进行了对比实验。图3显示了利用以上4种算法得到的分割结果。从图3可见,本文算法的分割效果最好。另外,本文选取了不同光照、尺度下的谷粒图像,利用四种算法进行分割实验,得到表1所示的分割准确率[5]。从表1可见,本文算法的平均分割准确率为94%,在四种算法中最高。