“拓扑”教学融通生长
2021-05-31强晓明
强晓明
【摘要】习题教学是数学教学中的一个重要组成部分.习题的设计常常会因为教学内容的不同而不同,但是,由于书本教学的分散性,很多有较强连续性的习题被人为地分割.那么,教师应该根据不同的课程类型设计相应的具有知识连贯性和拓扑性的习题去帮助学生进行理解,从而拓展学生的思维能力.
【关键词】小学数学;习题设计;拓扑;拓展思维
让学生巩固和消化知识,并且转化成技能的关键要素即习题.在实际教学过程中,习题成为教师了解和检查教学效果的金钥匙,学生把所学知识用于解决实际问题,从而展现其知识吸收能力.正因为习题如此重要,所以通过多年对练习状况的分析,笔者紧紧抓住“有效”两字,去除冗繁重复性练习,以培养学生数学素养为基准,深入拓展学生思维,设计有效的习题,从而实现教学的有效性.
数学知识不是孤立的存在,知识与能力的提升与拓展往往依附于课后的资料.一味地让学生去解题,会让学生浮于如何解答,而不去了解为什么这样解答,大部分学生会处于模模糊糊的状态,对于知识的理解完全没有固化.在教学过程中,教师如果能够由点出发,利用观察和联想,让学生由点成线,学生的思维自然能完整并且深刻.教师要做到以一题带一片,深挖习题中的思维价值,让学生主动拓展,激活其原本记忆中的知识,达到融合消化,使习题价值得到最大化发挥.
下面以苏教版六年级上册教材中的习题为例,谈谈具体的做法和想法.
片段一:切一切——初步感知表面积的变化特点
1.出示一个长8厘米、宽6厘米、高2厘米的长方体木块,请求出这个长方体的表面积和体积.
师:如果沿着长方体的长、宽、高切一刀,有几种切法?
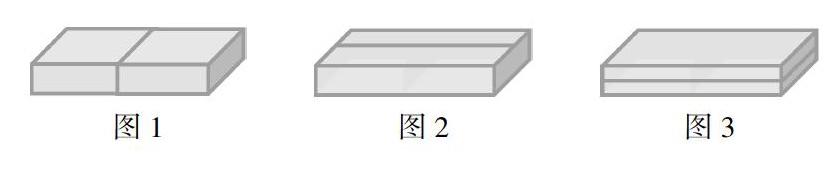
生1:我觉得可以在长的中点切,这样就可以得到2个长4厘米、宽6厘米、高2厘米的长方体木块.(如图1)
师:还有其他方法吗?
生2:我觉得可以在宽的中点切,这样就可以得到2个长8厘米、宽3厘米、高2厘米的长方体木块.(如图2)
生3:我觉得可以在高的中点切,这样可以得到2个长8厘米、宽6厘米、高1厘米的长方体木块.(如图3)
师:现在出现了3种不同的切法,我们继续思考,那么切好后的2个长方体的总表面积和原来长方体的表面积相等吗?
生:不相等,它们都变大了.
师:哪种表面积增加得最多?是多少?
生:不管是怎么切,表面积的和都会比原来多2个面的面积.在长的中点切,得到的这两个面积之和是(6×2×2=)24平方厘米;在宽的中点切,这两个面的面积之和是(8×2×2=)32平方厘米;在高的中点切,这两个面的面积之和是(8×6×2=)96平方厘米.因此,在高的中点切表面积增加得最多.
师:怎样才能快速地知道如何切表面积增加得最多?
生:切割面面积越大,表面积增加得越大;切割面面积越小,表面积增加得越小.
【思考】上面的教学侧重引导学生体会切割后图形的面积之和与原来长方体表面积相比发生了怎样的变化,以及发生相关变化的原因.为了降低学生的思考难度,教学时教师首先让学生先计算出原来长方体的表面积,然后通过课件上的动画,让学生直观地看到由于切的位置不同,所得到的长方体也可能不同.在教学中,教师多次让学生想一想切开后所形成的图形,从而培养学生的立体感.由此组织学生进一步观察、比较和分析,使他们在过程中认识到:之所以表面积会发生变化,是因为切的位置不同,导致剖面的大小不同.这样,学生不仅在切一切的过程中丰富和加深了对长方体表面大小的变化的理解,而且空間观念也得到了进一步的培养.
片段二:拼一拼——从不同方向丰富对表面积变化的认识
出示:再出示4个长8厘米、宽6厘米、高6厘米的长方体木块.
师:现在要把这4块长方体木块拼成一个大长方体,有很多种拼法,你觉得怎么拼得到的表面积最小?
师:请你拿出4个长方体木块,试着动手拼一拼.
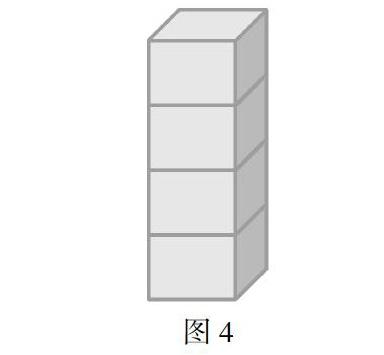
生1:我觉得像图4这样拼表面积最小.
师:说说你的想法.
生1:这样拼,长8厘米、宽6厘米的这个面一共重叠了3次,1次重叠2个面,这样得到现在图形的表面积就比原来少了(8×6×6=)288平方厘米.
师:有不同想法吗?
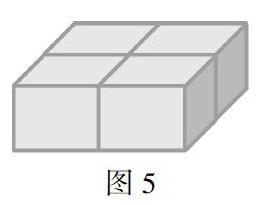
生2:我觉得像图5这样拼表面积最小.这里,长8厘米、高6厘米的这个面一共重叠了2次,少了4个面,这样比原来少了(8×6×4=)192平方厘米;宽6厘米,高6厘米的这个面一共重叠了2次,少了4个面,又比原来少了(6×6×4=)144平方厘米.
所以,表面积一共比原来减少了(192+144=)336平方厘米.
师:看来,不论是“切一切”还是“拼一拼”,仅仅根据重叠面的大小去判断表面积的增加和减少是不够的,有时候还需要结合重叠面的个数综合判断才行.
【思考】在这一个环节设计了“拼一拼”的操作练习,这个环节侧重引导学生从不同的方向去感受表面积变化的多样性.教学中,教师一方面鼓励学生借助已有的知识经验和实际操作主动探究解题方法;另一方面则注意借助课件的动态演示帮助学生体会多个组合图形表面积变化的特点.像这样,通过组合的方式不断刺激学生的数学神经,会更加有助于学生养成用整体和发展的眼光去看待不同数学现象的意识,从而丰富学生的空间意识.
片段三:想一想——在想象中提高空间思维能力
出示一个棱长4厘米的正方体,把每条棱都平均分成4份,从而平均分成64个棱长1厘米的小正方体,从正方体的一个顶点处去掉一个小正方体,求现在这个图形的表面积.(如图6)
师:想一想,这个图形的表面积是多少?
生1:表面积比原来少了4平方厘米.
师:大家有其他想法吗?
生2:表面积没有变.去掉一个小正方体以后比原来少了3个面,但是内部又多出来3个面(3-3=0),因此,现在图形的表面积和正方体的表面积相等.
出示第二个图形(如图7).
师:如果从正方体的棱上拿走一个小正方体,如图7,表面积有什么变化呢?
生:表面积比原来多了2平方厘米.去掉一个小正方体以后比原来少了2个面,但是内部多出来4个面(4-2=2),现在图形的表面积比正方体的表面积增加了2平方厘米.
师:从正方体的一个面上拿走一个小正方体,如图8,表面积又会有什么变化呢?
生:表面积比原来多了4平方厘米.去掉一个小正方体比原来少了1个面,内部多出来5个面(5-1=4),因此,现在图形的表面积比正方体的表面积增加了4平方厘米.
对比发现:仔细观察这3组图,结合刚才的思考过程,你有什么发现?
得到:无论是在顶点处还是在棱上、面上去掉一个小正方体,都只要思考和原来比少了几个面,再思考现在比原来又多出来几个面,然后再计算就可以了.
师:现在老师这还有一道课后题,请同学们课后自己思考.(出示课后题,如图9)
【思考】这道题是对学生空间思维能力考查的重要题型.本道题分成了2个层次:第一,分别从顶点、棱、面上去掉一个小正方体,研究现在图形和原来图形表面积之间的變化情况.得到:①在顶点处,表面积不变;②在棱上,比原来多2个面;③在面上,比原来增加了4个面.第二,分别去掉一行小正方体,由于位置的不同,表面积发生的变化也不同.当学生思考有困难时,教师要充分借助课件,通过课件的展示帮助学生理解和思考,从而将一些抽象的图形具象化,使得学生在今后解决较抽象的习题时能有一定的思维伸展性.虽然这次所教的是一群农村孩子,但是,让他们经历这样的活动过程,他们所获得的不仅仅是解决某个具体问题的思考经验,更是一种具有生成性的数学思考方法.
教师不能只关心习题的量,而忽略知识点的联系及融合,尤其是小学高年级的老师,应该让学生学习知识的积累,思维的拓展,能力的融合固化.案例中教师引导学生讲解解题后的自我感触,达到知识的反馈体现,既完成了习题的基本要求,又让学生感受到等量关系在解方程中的巨大作用.总之,在数学习题教学中,教师应建立系统科学的框架体系(即相关知识点的串联讲解),注意教材理论与习题之间的联系,让学生在有效的习题过程中习得经验,养成习惯,让学生愿意去探究和思考数学问题.
【参考文献】
[1] 苏桂芹,李秀珍.小学数学练习课六步教学模式的探索[J].小学数学教育,2015(05):16-17.
[2] 郑伟.基于多学科融合的学生空间观念的培养:以“平移、旋转和轴对称”练习课教学为例[J].西部素质教育,2020(06):76.
[3]单俊宁,鞠喜见.小学数学教学中有效问题情境的创设[J].教学管理与教育研究,2017,2(11):93-94.
[4]刘桂芝.例析小学数学课堂练习的问题切入[J].教学管理与教育研究,2019,4(24):90-92.
