不同排水条件下非饱和土中柱孔扩张问题的解析分析1)

周凤玺 牟占霖 杨汝贤 张雅森

∗(兰州理工大学土木工程学院,兰州 730050)

†(西部土木工程防灾减灾教育部工程研究中心,兰州 730050)

∗∗(甘肃建投建设有限公司,兰州 730050)

引言

圆孔扩张理论最先由Bishop 等[1]提出用来解决金属压痕问题,被Vesic[2]将其引入岩土与地下工程领域后,在诸如旁压和圆锥贯入试验问题[3-4]、石油工程中井筒稳定性的鉴定[5-6]、桩轴和地锚承载力的确定[7]以及沉桩扩孔和静力触探[8-13]等工程实践中得到了普遍应用,同时也促进了圆孔扩张理论的长足发展.

圆孔扩张问题的现有解答大多数都是建立在饱和土体基础上提出的[14-18],因而对于非饱和土地区的实际工程问题缺乏指导意义.首先,非饱和土是多相混合体,土中吸力会显著影响圆孔扩张后周围土体中应力场的分布,且不同于饱和土体,超孔隙水压力在非饱和土中难以产生,尤其在不同排水条件下,土体的体积变化情况对土体中应力应变场分布成为关键影响因素.现有对于非饱和土中圆孔扩张问题的研究中,Russell 和Khalili[19]采用有效应力和界面塑性理论的概念,在临界状态框架下建立统一的本构模型并考虑吸力和颗粒破碎的影响,对非饱和土圆孔扩张问题进行了求解,但其采用的是相对复杂的边界面模型,最终使用相似解技术得到了两种不同土壤条件下的球柱形小孔扩张的半解析解;胡伟等[20-21]考虑了土体体积变化的影响,结合修正剑桥模型推导出了非饱和土中球形孔扩张后土体中应力、位移分布的解析解,但其未将净应力和吸力的作用效应分开考虑,认为球孔扩张是在净应力和基质吸力耦合作用下发生的,忽略了吸力的影响;Yang 和Russell[22]使用相似解技术对非饱和粉砂的圆孔扩张进行分析,在分析中,孔隙比、吸力、饱和度和有效应力作用是完全耦合的,此外,他研究了3 种不同排水条件(恒定吸力、恒定含水量和吸力对有效应力的恒定贡献)对空腔壁压的影响,发现排水条件下吸力的影响与其他两个条件非常接近.目前,非饱和土圆孔扩张问题的解答多是基于修正剑桥模型和边界面塑性模型进行分析,很少考虑土体中的中间主应力在圆孔扩张中的影响.鉴于此,赵均海等[23]利用统一强度理论,合理考虑中间主应力和基质吸力的效应,得到了非饱和土中柱孔扩张问题的统一弹塑性解,并与现有的基于M-C 准则的公式进行对比验证,但上述成果并未分析不同排水条件下柱孔周围土体体积变化及土体剪胀对于周围弹塑性区应力应变场分布的影响.

基于以上研究基础,本文将采用统一强度理论,视非饱和土体为均匀且各向同性的弹塑性材料,将柱孔周围土体分为弹性区和塑性区,并提出在弹性区遵循小应变理论,在塑性区遵循大应变理论,以得到综合考虑中间主应力、吸力、不同排水条件及土体剪胀等影响因素下的非饱和土中柱孔扩张时周围弹塑性区内应力场和应变场分布规律与最大塑性区半径及极限扩孔压力的解析解,通过与已有的饱和及非饱和土中柱孔扩张解答进行退化验证与对比计算来证明解答的有效性,以期为非饱和地基压力注浆、复合地基处理等设计提供合理的理论参考依据.

1 柱孔扩张模型

实际工程中,非饱和土地基进行压力注浆时,浆柱与周围土壤存在明显的分界面,在均匀土壤中,其近似于柱状,水泥浆的膨胀会导致紧邻膨胀桨柱的注浆土壤区域在径向和切向有效应力作用下出现严重的破坏区,即剪切和塑性变形.随着土壤与注浆界面距离的增大,变形基本变为弹性.考虑一种理想情况,钻孔后将浆液注入地面,而不干扰周围土壤,并将注浆管牢固地密封在周围地面上,从而使上述问题变为一个典型的柱孔扩张问题.

非饱和土中柱孔扩张模型示意图如图1 所示.柱形孔初始半径为a0,承受初始内压力p,当内压从初始内压力p增大至极限有效孔压时,小孔半径达到最终扩孔半径au,此时塑性区半径为rp,塑性区范围为au≤r≤rp,弹性区范围为r≥rp.图中urp为扩孔后弹性区与塑性区交界处的位移,和分别为径向有效应力和切向有效应力,rp0为弹塑性交界面在扩孔前距孔中心的距离,为作用在周围的初始径向有效应力.

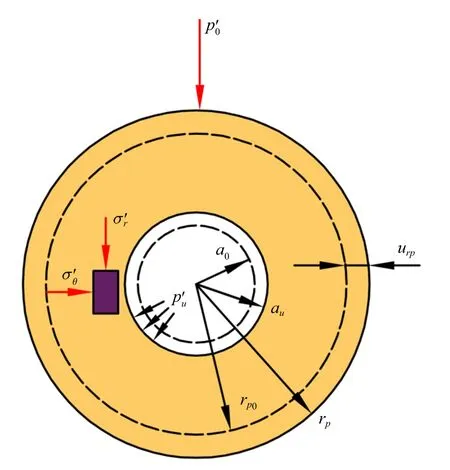
图1 柱孔扩张模型示意图Fig.1 Schematic diagram of the expansion of cylindrical cavity model

1.1 基本假定

在对非饱和土在排水条件及不排水条件下的柱孔扩张问题的弹塑性解析中,作出以下几点假设:

(1)非饱和土体是均匀的且各向同性的弹塑性材料,且在发生柱孔扩张前

(2)充分考虑中间主应力效应对不同应力条件下的土体发生屈服及破坏的影响,柱孔周围土体屈服服从统一强度准则;

(3)扩孔过程中,土体在弹性区遵循小应变理论,在塑性区遵循大应变理论.

1.2 基本方程

1.2.1 有效应力原理

非饱和土的有效应力原理是非饱和土力学的核心,目前有以单应力状态变量[24]、双应力状态变量[25]和复合应力状态变量[26]表示的有效应力公式.其中Lu 等[27]在考虑颗粒间相互作用力的基础上,提出了简化后的有效应力表达式为

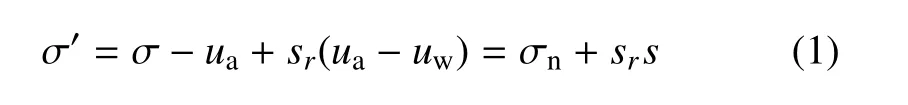
式中,σ′为有效应力,ua为孔隙气压力,uw为孔隙水压力,sr为土体饱和度,σn=σ-ua为净法向应力,s=ua-uw为基质吸力.

1.2.2 非饱和土抗剪强度理论

将式(1) 代入有效应力表示的抗剪强度公式,可得

式(2) 表明非饱和土的抗剪强度随净法向应力的增大而增大,并且由于饱和度对粒间吸力的影响使得基质吸力的增大引起了非饱和土黏聚力的增大.

1.2.3 几何方程

弹性区遵循小应变理论的几何方程为

式中,εr,εθ分别为径向应变与切向应变;u为土体位移;r为土体半径.

在塑性区根据大变形理论可得几何方程为

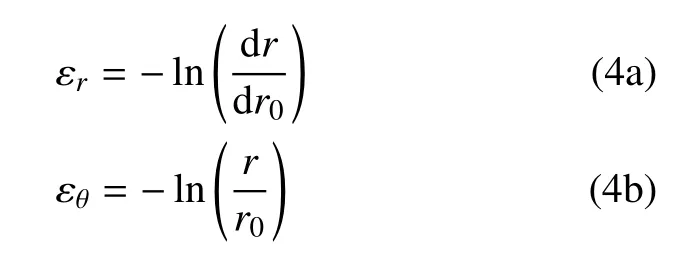
式中,r0为土体内任意某一土体单元距离柱孔中心的初始半径距离;r为这一单元扩孔后的半径.

1.2.4 本构方程

考虑非饱和土中的柱形扩孔问题属于平面应变问题,则本构关系用有效应力形式表示为

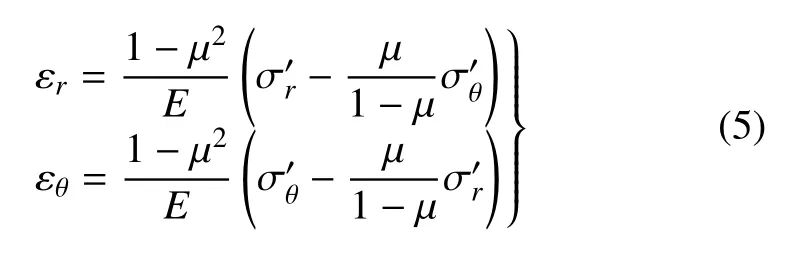
式中,E为材料的弹性模量,µ为泊松比.

1.2.5 微分平衡方程

小孔周围土体的应力关系满足下式

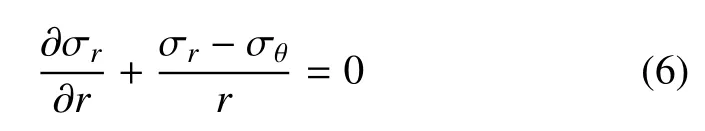
结合式(1)和式(6)可得到用有效应力表示的小孔周围土体满足的平衡方程为

式中,η 代表折减系数,η=1+(s/sr)(∂sr/∂s).

1.2.6 屈服准则

根据统一强度理论[28],用有效应力表示的非饱和土屈服准则为

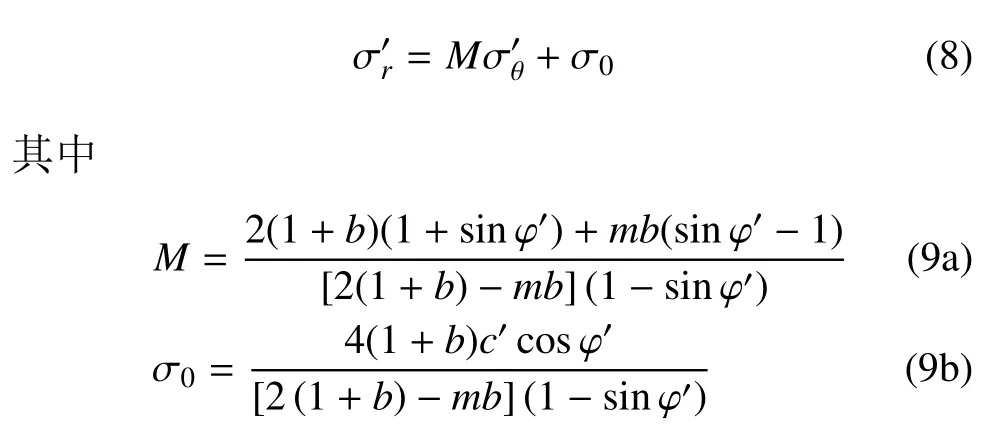
式中,c′为土体有效黏聚力;φ′为有效内摩擦角;b为表征中间主应力效应的参数,可由试验测定,通常取值范围为0～1;m为中主应力参数,在平面应变条件下m≤1,当土体进入塑性状态时m→1.

2 排水条件下的弹塑性解答

排水条件下考虑恒定吸力s的情况[19],可得到

结合式(7),排水条件下的平衡方程为

2.1 弹性区解答

2.1.1 弹性区应力场解答

弹性区的应力边界条件为

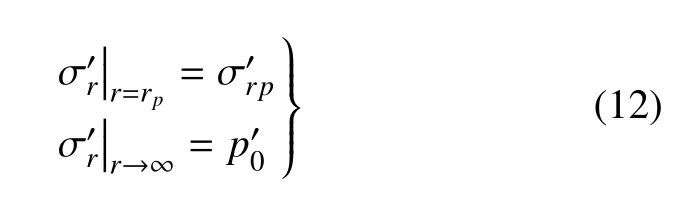
结合式(11) 和式(12) 可解得弹性区内有效应力场如下

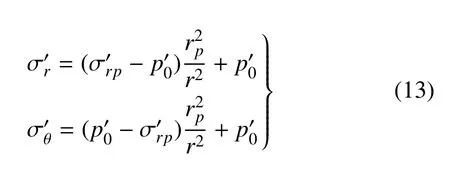
2.1.2 弹性区应变场及位移场解答

结合式(3b)、式(5)、式(13)及假设(1),最终可得弹性区内的应变场及位移场解答如下

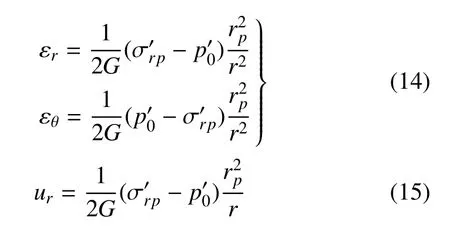
式中,G=E/[2(1+µ)]为材料的剪切模量.结合应力边界条件,并将弹性区内的有效应力场式(13) 代入式(8),可得弹塑性交界面上的径向及切向有效应力如下

2.2 塑性区解答

2.2.1 塑性区应变场解答

在塑性区应变场问题中,径向与切向的总应变包括弹性应变和塑性应变两部分,表示如下

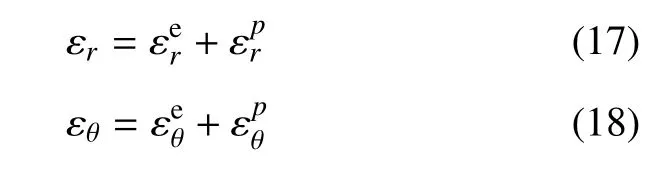
将式(16)代入式(15)可得弹塑性交界面上的径向位移为

结合式(3a)、式(3b)可得弹塑性交界面上的径向及切向的极限弹性应变为

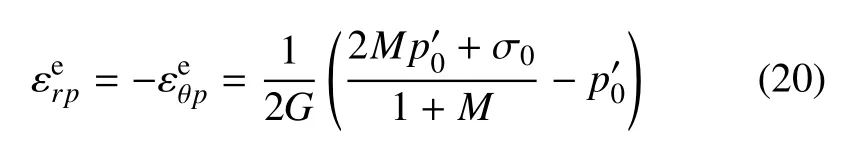
本文中在塑性区采用非关联流动法则,因为塑性区内弹性应变相对于塑性应变很小可忽略,所以在塑性区内的径向塑性应变与切向塑性应变有如下关系

式中,h为剪胀特性参数,h=(1+sin ξ)/(1-sin ξ);ζ为土体剪胀角,用来表示土体在剪切过程中体积变化率的一个物理量.

联立式(4a)和式(4b)、式(17)和式(18)及式(20)和式(21)可得塑性区内的位移协调方程为

结合式(26)及式(32)可得,非饱和土柱形扩孔问题的极限扩孔压力的解答如下

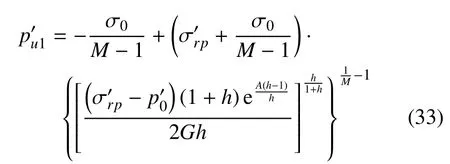
3 不排水条件下的弹塑性解答

3.1 弹性区解答

本文为了分析不排水条件下柱孔扩张时周围弹塑性区内应力场,定义

因此,排水情况下的弹性区内的解答在不排水条件下同样适用.

3.2 塑性区解答

3.2.1 塑性区应变场解答

柱孔孔径从r0扩张到r,体积应变的表达式为

不排水条件下柱孔扩张时,当非饱和土中的气压保持不变,土体是等容变形,其塑性区域内的体积应变及体积应变率均为0,即

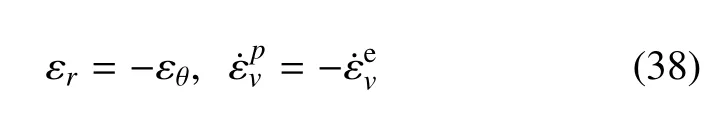
联立式(4a)、式(4b)、式(38)及式(45)可得不排水条件下柱孔周围塑性区内应变场如下

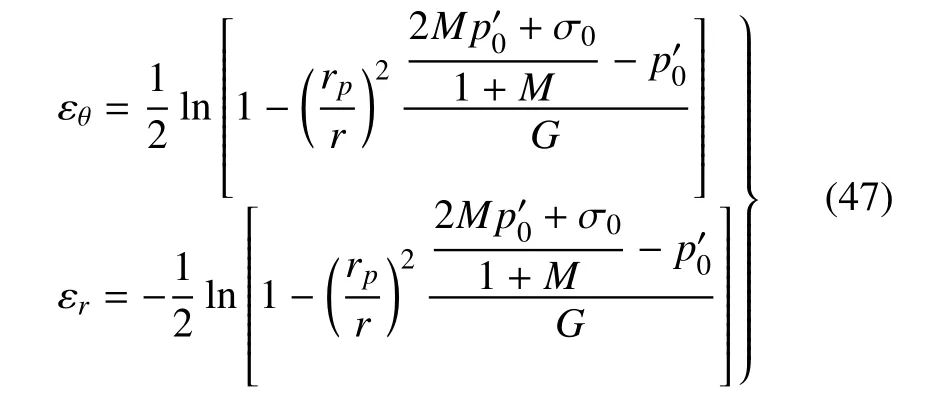
由式(20)可得塑性区内径向及切向塑性应变表达如下

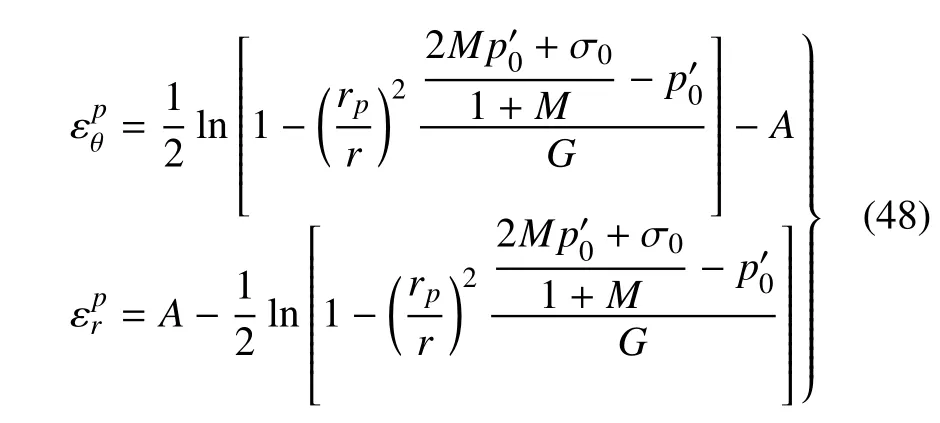
3.2.2 塑性区应力场解答

为解答柱孔周围塑性区应力场分布,假设不排水条件下非饱和土柱孔扩张时塑性区中的屈服条件(式(48))和塑性流动法则(式(49))分别为

将式(56)代入式(8)可得用p′与q′表示的屈服准则

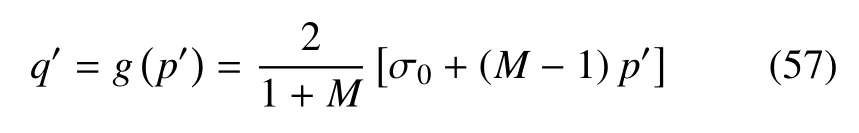
式(35)中得体积模量K及剪切模量G可分别表示为

式中,v为非饱和土体的比体积;κ 为非饱和土在v-p′平面上的加载-再加载线的斜率;根据体积模量,剪切模量及弹性模量间的关系,可得β 表达式为:β=3(1-2µ)/[2(1+µ)].

运用正交流动法则计算塑性区内的塑性体积应变率和塑性剪切应变率,代入式(50),可得

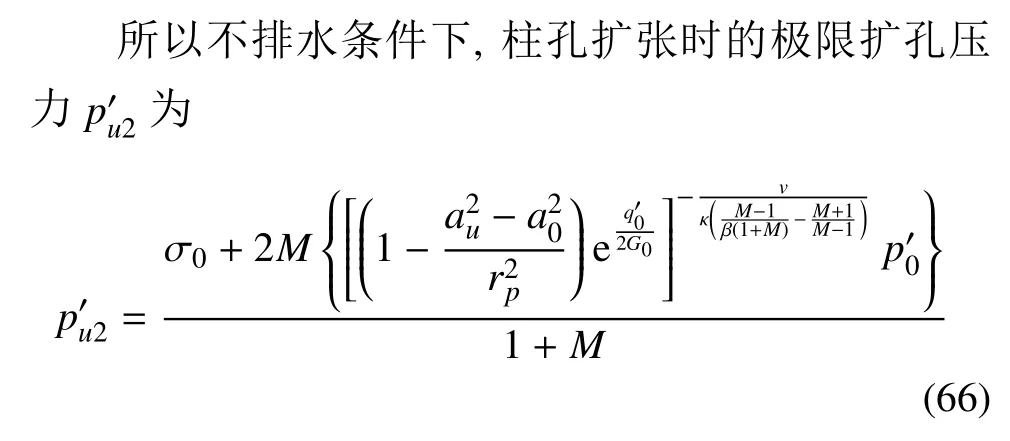
4 解答的有效性验证

4.1 排水条件

为了验证排水条件下极限扩孔压力理论解的有效性,利用式(33) 得出的极限扩孔压力的解答,与文献[2] 得到饱和土中的柱形扩孔问题的极限扩孔压力的结果进行比较.图2 绘出了当E=6000 kPa,µ=0.3,φ′=14°,c=20 kPa,m=1,b=0,h=1,s=0时的极限扩孔压力结果对比.

图2 不同 与h 下文献[2]解与本文解的对比Fig.2 Comparison of the solution in Ref.[2]and the solution in this article under different and h

从图2 可以看出,h=1 时,在同等初始有效应力下本文理论解略大,但随着初始径向有效应力的增加,二者的解的值都在递增且逐渐吻合,反映了对极限扩孔压力的影响,随着的增大,柱孔扩张时需要更大扩孔压力克服初始有效应力的影响.同时由于本文得到的排水条件下极限扩孔压力解答考虑了土体剪胀对极限扩孔压力的影响,不单一受的影响,所以在同一下,随着h值不断增大,本文解与文献[2]间的差值愈大,其原因是此时土体需要更大扩孔压力来克服土体剪胀特性的影响,亦印证了排水条件下本文解充分考虑剪胀效应的必要性.

4.2 不排水条件

对于不排水条件,利用文献[30] 得到的柱孔扩张中极限扩孔压力与本文得到的不排水下的解答式(66) 进行对比验证如图3 所示.选取计算参数E=6000 kPa,µ=0.3,φ′=14°,c=20 kPa,m=1,b=0,v=2.0,a0=0.05 m,κ=0.062,au=0.1 m.

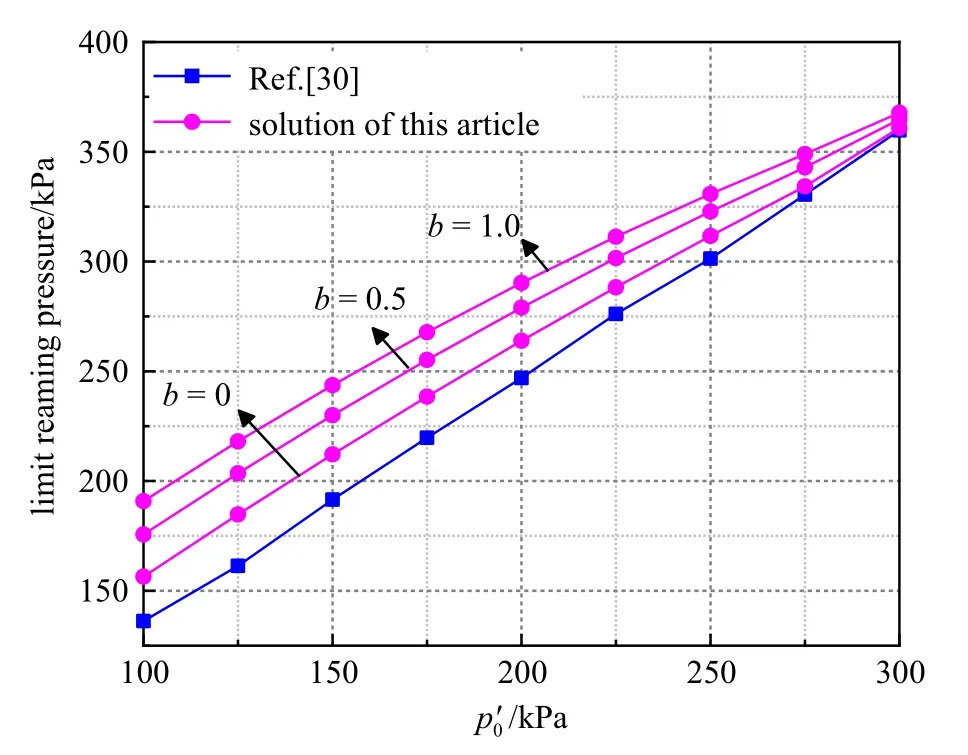
图3 不同及b 下文献[30]解与本文解的对比Fig.3 Comparison of the solution in Ref.[30]and the solution in this article under differentand b

从图3 可以看出,本文所得到的不排水情况下的理论解较文献[30]的理论解存在一定差别,这是因为文献[30]的理论解是基于M-C 强度理论得出的,并未考虑中间主应力在柱孔扩张中的影响,但此处为验证本文解的有效性,首先将参数b退化为0,从而弱化了中间主应力效应,使得随着的增大,本文解与文献[30]解间的差异弱化,逐渐吻合,而后相继改变b值,可以看到随着b值增大,本文解与文献[30]解在同一时,相对误差变大,从而验证了本文充分考虑中主应力效应的必要性及有效性.

上述现有的扩孔理论在岩土工程领域有着广泛的应用,例如确定地基的极限承载力,分析沉桩、静力触探,隧道开挖及支护等土工问题.对比分析本文柱孔扩张理论与现有理论,可以看出,本文理论以统一强度理论和大小应变理论为出发点,综合考虑中主应力、吸力、土体剪胀等因素,对非饱和土体在排水及不排水下的扩孔问题进行研究,最终将研究成果在现有应用领域的基础上,进一步应用于注浆机理分析和注浆压力的预估,以指导非饱和土地基压力注浆、复合地基处理等实际工程问题.

5 参数分析与讨论

5.1 排水条件

5.1.1 弹性区参数分析

在数值算例中,土体的物理力学参数取值为φ′=25°,E=3000 kPa,µ=0.3,m=1,v=2.0,κ=0.062,a0=0.1 m,a=0.2 m.

考虑在柱孔周围的初始径向有效应力=80 kPa,图4 和图5 分别给出了排水条件下不同吸力时弹性区径向及切向有效应力与rp/r和b之间的变化关系.

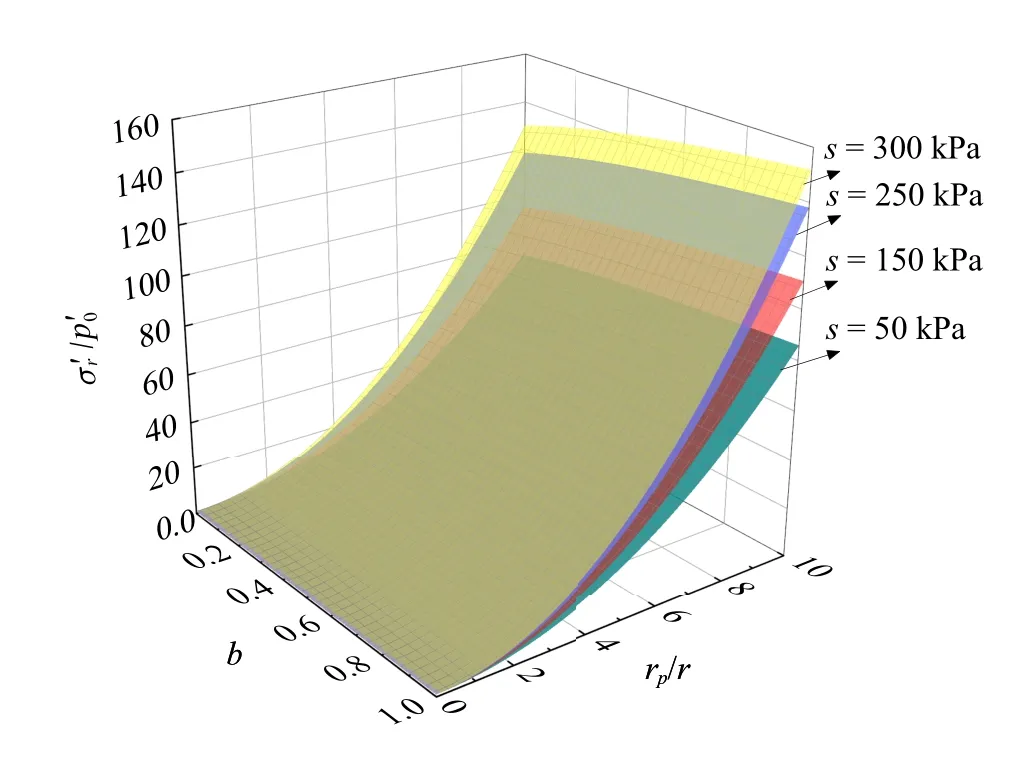
图4 不同吸力下弹性区径向有效应力与rp/r 和b 之间的变化Fig.4 Radial effective stress of the elastic zone and the change between rp/r and b under different suction

从图4 和图5 可以看出,当参数b和rp/r一定时,随着吸力的增大,弹性区径向及切向有效应力均随其非线性增加;同一吸力下,控制参数b或rp/r一项影响因素保持不变,径向及切向有效应力均随另一因素递增.

图5 不同吸力下弹性区切向有效应力与rp/r 和b 之间的变化Fig.5 Tangential effective stress of the elastic zone and the change between rp/r and b under different suction

在给定初始吸力s0=50 kPa,不同初始径向有效应力下弹性区径向及切向有效应力与rp/r和b之间的变化趋势如图6 和图7 所示.

图6 不同初始径向有效应力下弹性区径向有效应力与rp/r 和b 之间的变化Fig.6 Radial effective stress of the elastic zone and the change between rp/r and b under different initial radial effective stress

从图6 和图7 可以看出,当参数b和rp/r一定时,随着初始径向有效应力的增大,弹性区径向及切向应力均随其非线性增大;同一初始径向有效应力下,控制参数b或rp/r一项因素保持不变,径向及切向应力均随另一因素递增.

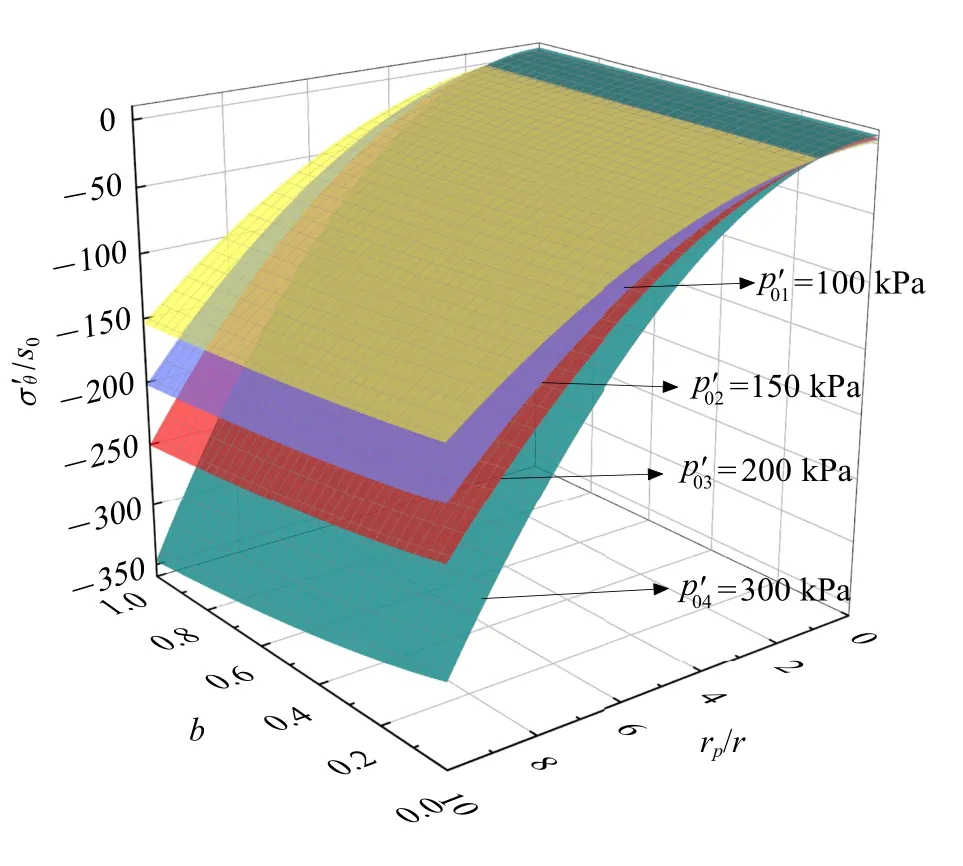
图7 不同初始径向有效应力下弹性区切向有效应力与rp/r 和b 之间的变化Fig.7 Tangential effective stress of the elastic zone and the change between rp/r and b under different initial radial effective stress

以上分析表明,非饱和土中,吸力、中主应力及初始径向有效应力对弹性区内的应力场分布影响显著.

5.1.2 塑性区参数分析

给定作用在柱孔周围的初始径向有效应力=80 kPa,图8 和图9 所示分别为不同吸力下塑性区径向及切向有效应力rp/r与和b之间的变化趋势.

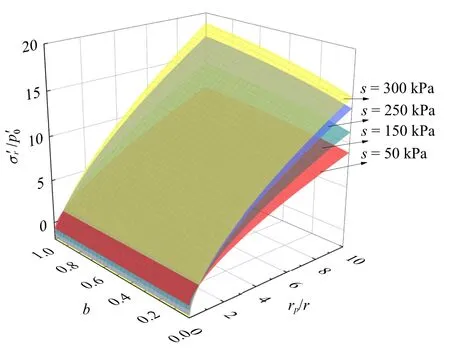
图8 不同吸力下塑性区径向有效应力与rp/r 和b 之间的变化Fig.8 Radial effective stress of the plastic zone and the change between rp/r and b under different suction

从图8 和图9 可以看出,rp/r一定时,b对应力场的影响甚微,而当b一定时,切向及径向有效应力随着rp/r的增大而递增,且当rp/r和b一定时,应力场随着s的增大而递增.

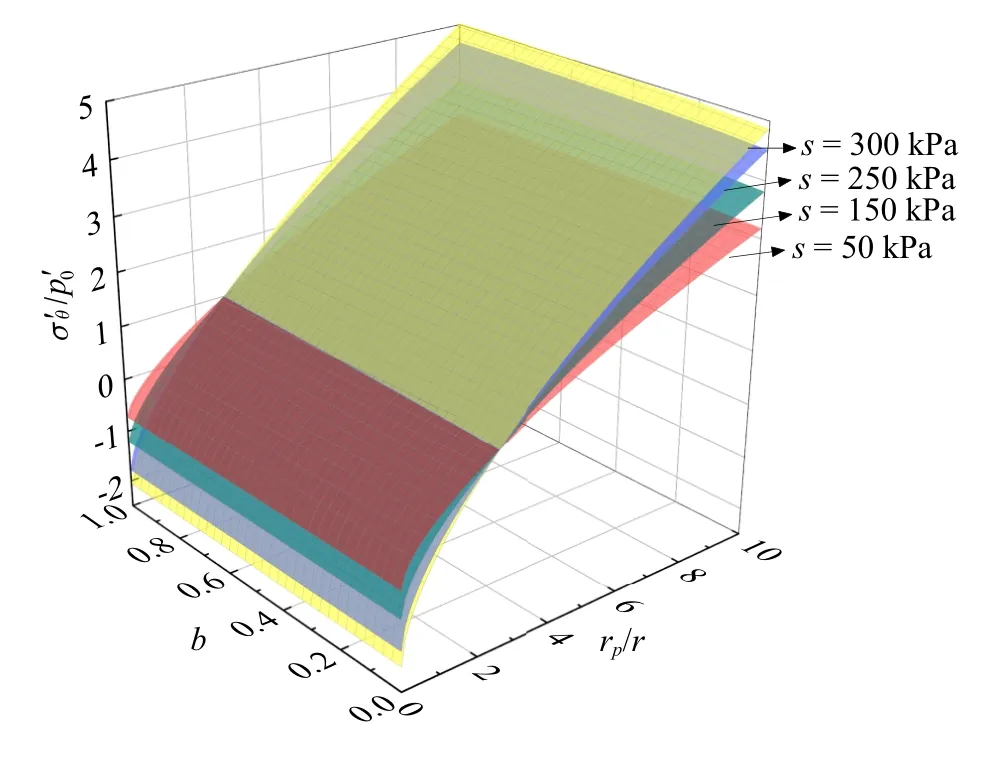
图9 不同吸力下塑性区切向有效应力与rp/r 和b 之间的变化Fig.9 Tangential effective stress of the plastic zone and the change between rp/r and b under different suction

考虑土体吸力s=50 kPa,初始径向有效应力=100 kPa,r0=10 m.图10 和图11 为塑性区径向及切向应变在不同剪胀系数下与参数b之间的变化曲线.

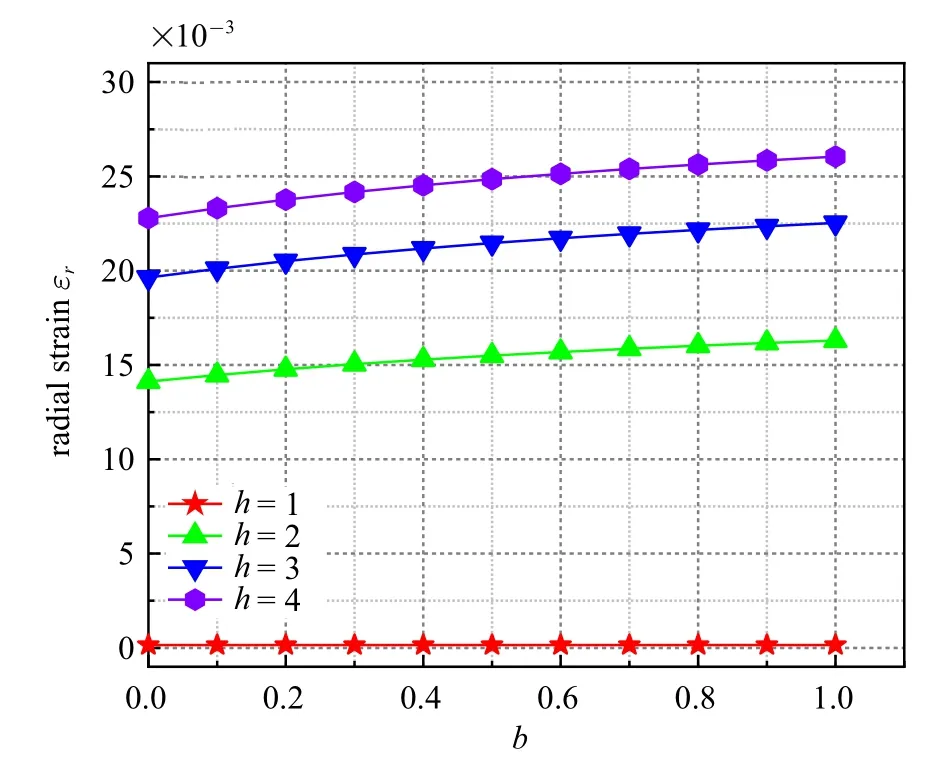
图10 不同剪胀参数下塑性区径向应变与b 之间的变化Fig.10 Change between the radial strain of the plastic zone and b under different dilatancy parameters

从图10 和图11 可以看出,参数b的变化对应变场的影响很小,尤其对于切向应变,因此分析变形时可以不用过多考虑其影响;而剪胀参数则影响显著,随着剪胀参数的递增,径向及切向应变均随之增大.可以看出,对排水条件下的塑性区进行弹塑性进行分析,综合考虑大变形、土体剪胀及中主应力等因素的必要性.

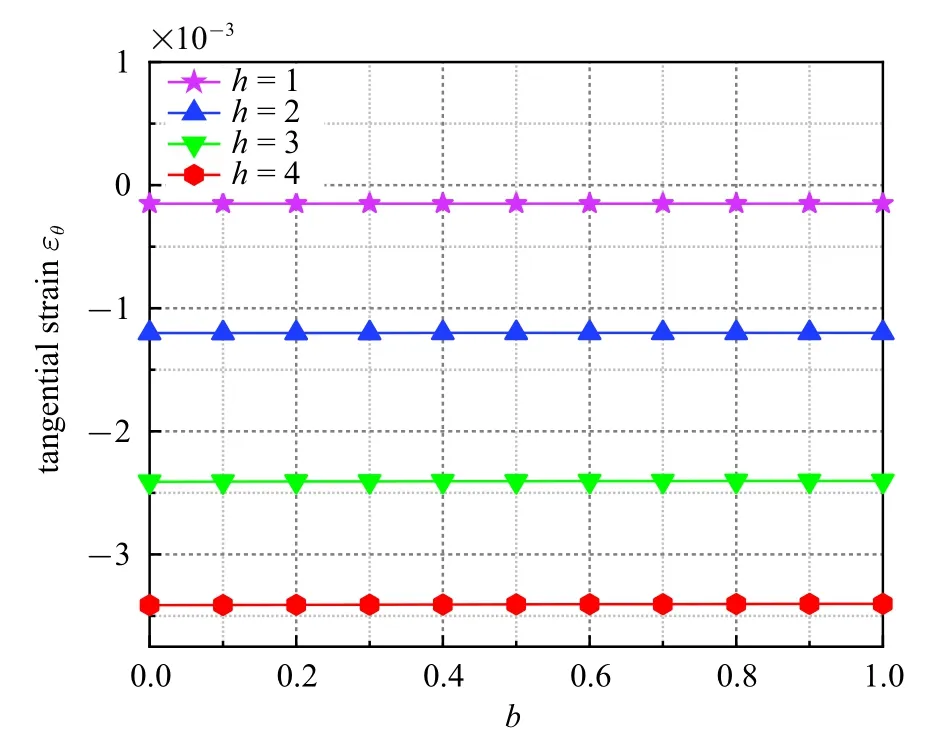
图11 不同剪胀参数下塑性区切向应变与b 之间的变化Fig.11 Change between the tangential strain of the plastic zone and b under different dilatancy parameters

5.1.3 极限扩孔压力参数分析

当土体初始吸力s0=50 kPa 且=100 kPa 时,图12 给出了极限扩孔压力在不同剪胀系数下与参数b之间的变化关系.

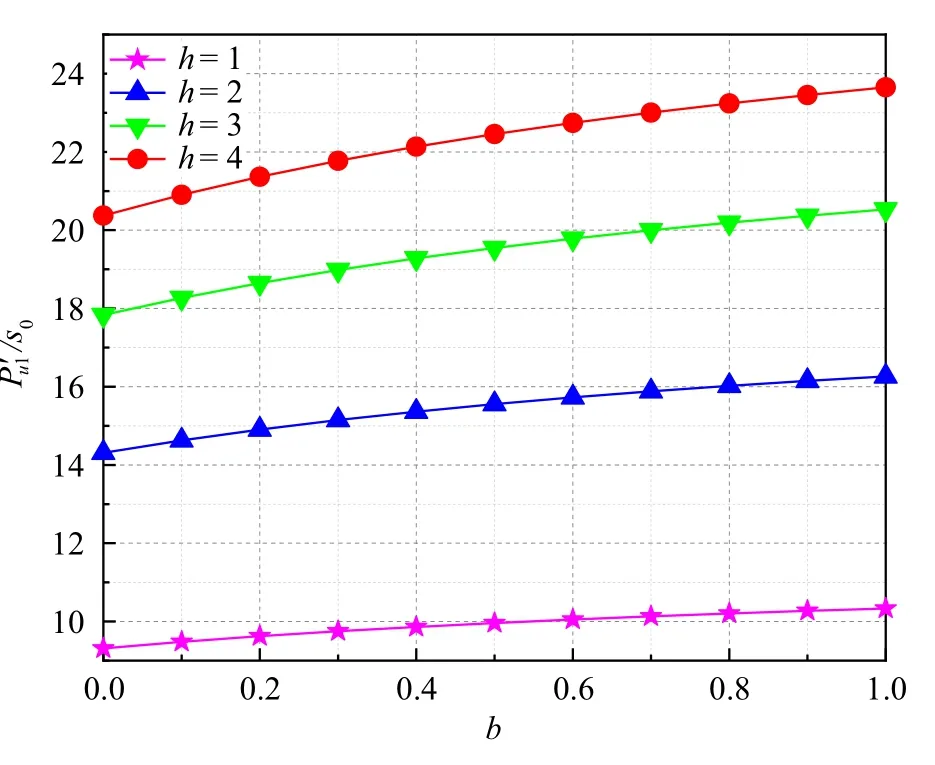
图12 不同剪胀参数下极限扩孔压力与b 之间的变化Fig.12 Change between the limit reaming pressure and b under different dilatancy parameters

从图12 可以明显看出,同一参数b,随着剪胀参数的增大,扩孔压力显著递增;h一定时,随着参数b的增大,扩孔压力呈非线性增长.

5.1.4 最大塑性区半径参数分析

当土体初始吸力s0=50 kPa 且=100 kPa 时,图13 给出了最大塑性区半径在不同剪胀参数下与参数b之间的变化曲线.

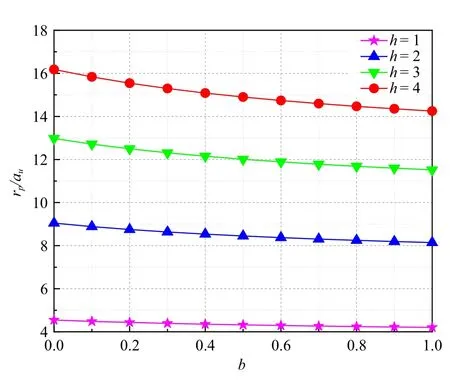
图13 不同剪胀参数下最大塑性区半径与b 之间的变化Fig.13 Change between the maximum plastic zone radiu and b under different dilatancy parameters

从图13 可以明显看出,参数b对于rp的影响随着剪胀参数的增大而逐渐显著,而参数b一定时,剪胀参数h的增大引起了rp的显著增大.

以上可以分析可知,对于和rp,中主应力及剪胀参数均对其影响显著,尤其是土体剪胀特性更应作为实际工程中考虑的重点因素.

5.2 不排水条件

5.2.1 塑性区参数分析

同样选取土体吸力s0=50 kPa,初始径向有效应力=100 kPa,图14 和图15 为在不同初始径向有效应力下,塑性区径向及切向应变与rp/r和参数b之间的变化.

图14 不同初始径向有效应力下塑性区径向应变与rp/r 和b 之间的变化Fig.14 Radial strain of the plastic zone and the change between rp/r and b under different initial radial effective stress

从图14 和图15 可以看出,径向及切向应变随着参数b及rp/r的增大而增大,随着增加变化趋势更加显著.而当b及rp/r一定时,递增,径向及切向应变相应增大.显然,对于不排水条件下的塑性区应变场分布,中主应力,半径比及初始径向有效应力均影响显著,且这种趋势随着的递增愈加显著.

图15 不同初始径向有效应力下塑性区切向应变与rp/r 和b 之间的变化Fig.15 Tangential strain of the plastic zone and the change between rp/r and b under different initial radial effective stress

当初始吸力s0=50 kPa 时,在不同初始径向有效应力下,塑性区径向及切向应力与r/a和参数b之间的变化如图16 和图17 所示.

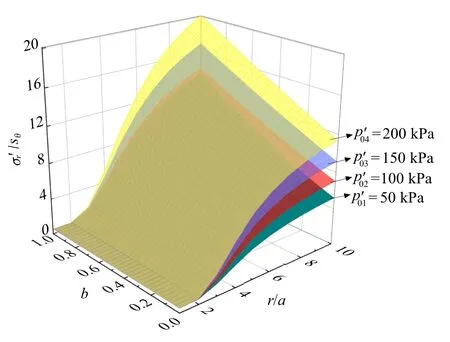
图16 不同初始径向有效应力下塑性区径向有效应力与r/a 和b 之间的变化Fig.16 Radial effective stress of the plastic zone and the change between r/a and b under different initial radial effective stress

图17 不同初始径向有效应力下塑性区切向有效应力与r/a 和b 之间的变化Fig.17 Tangential effective stress of the plastic zone and the change between r/a and b under different initial radial effective stress

5.2.2 极限扩孔压力参数分析

为了分析参数au和b对极限扩孔压力的影响.图18 所示为在=100 kPa 时,不同初始吸力s0下极限扩孔压力的变化.

图18 不同初始吸力下极限扩孔压力与b 之间的变化Fig.18 Change between the limit reaming pressure and b under different initial suction

从图18 可以明显看出,同一参数b下,随着初始吸力s0的增大,扩孔压力显著递增,说明土体出现吸力硬化的现象;不同于排水情况,当s0一定时,扩孔压力随着参数b明显减小,中主应力的效应随着b的增大而显著.

5.2.3 最大塑性区半径参数分析

取吸力s=50 kPa,图19 所示为在不同初始径向有效应力下,最大塑性区半径与au和参数b之间的变化.

从图19 可以看出,rp随着参数b的增大而递减,且这种趋势随着的增大而愈加清晰,而当参数b一定时,rp随着的增大而递增.显然,对于最大塑性区半径,参数b及均对其影响显著,因而进行不排水条件下柱孔周围土体变形分析时,二者的影响作用应共同考虑.

图19 不同初始径向有效应力下最大塑性区半径和参数b 之间的变化Fig.19 Change between the maximum plastic zone radiu and b under different initial radial effective stress

6 结论

本文针对非饱和土中柱孔扩张问题,通过理论分析,得出了排水及不排水情况下柱孔周围弹塑性区内的应力场、应变场及位移场解答,并进行了参数分析,得出以下结论:

(1)排水情况下,弹性区内径向及切向应力均随着rp/r和b的增大呈非线性增大,且在不同s及下,径向及切向有效应力均随着二者的增大而增大,以上反映了中主应力及吸力的效应;塑性区内,参数b对于应变场影响甚微,尤其对于切向应变,因此对塑性区进行变形分析时可不过多考虑其影响;同时,随着参数b的增大,亦随之递增,这种趋势伴随着剪胀效应的显著而愈加清晰,这是由于b和h的增大,需要更大的扩孔压力来克服中主应力和土体剪胀特性的影响,同样,最大塑性区半径rp也随着土体剪胀的发生而逐渐增大,因此土体剪胀对变形的影响应是理论应用的过程中重点考虑的问题.

(2)不排水情况下,弹性区整体变化趋势同排水情况,塑性区则不同.塑性区内,径向及切向应变随着参数b及rp/r的增大而增大,随着增大变化趋势愈加明显,显然排水条件及亦对应变场分布影响显著.对于应力场,存在r/a=3 这个应力转折点,参数b对应力场的影响在转折点前后显著不同;对于及rp,随着s0增大,引起了c′的增大,导致及rp亦随其递增,而参数b的增大意味着中主应力对于土体破坏效应增强,因而及rp随着参数b递增而减小.