基于LBM 的壁湍流跨尺度能量传递结构统计1)

高 铨 邱 翔,,2) 夏玉显 李家骅 刘宇陆,

∗(上海应用技术大学理学院,上海 201418)

†(上海应用技术大学机械工程学院,上海201418)∗∗(上海应用技术大学城市建设与安全工程学院,上海 201418)

††(上海大学力学与工程科学学院上海市应用数学和力学研究所,上海 200072)

引言

壁湍流近壁区多尺度相互作用近年来一直是湍流研究的热点领域[1-3].在壁面附近,湍流各尺度间的能量传输机理与近壁相干动力循环密切相关,对于高保真大涡模拟技术而言,研究并利用壁湍流多尺度能量传输机制,对于建立能够准确刻画近壁区相干结构演化的壁模型具有极其重要的意义[4-5].大量的数值和实验通过在物理空间滤波获取不同尺度间的能量传递研究了壁湍流跨尺度能量传递机制[6-20].H¨artel 等[7]通过物理空间滤波在近壁区缓冲层内发现了由亚格子尺度向可解尺度进行的能量反级串现象,认为这种反传现象的主要成因是平均速度产生的能量与亚格子尺度耗散作用在截断波数附近重合在一起,没有完全分开.通过条件统计发现,近壁区的相干运动如:猝发,可以显著增强近壁区的能量反传.Piomelli 等[8]应用条件统计方法进一步发现能量的正反传事件与壁湍流的典型结构如:准流向涡、发卡涡以及上抛和下扫等结构密切相关.在缓冲层内,正传事件伴随上抛结构,反传事件伴随下扫结构,正反传事件出现在沿流向略微抬起一定角度的拟流向涡两侧.H¨artel 等[7]和Piomelli 等[8]的研究都表明:Smargorinsky 涡黏模型并不能准确刻画近壁区能量正反传事件.Lin[9]通过对平板边界层的大涡模拟进一步解释并支持了Piomelli 等[8]的结果.而Germano等[10]提出的Dynamic Smagorinsky 模型以及后来的混合模型、多尺度模型则可在一定程度上刻画近壁区的能量反传事件,但各个模型和实验间依然存在一些差异.Tian 等[11]通过对湍动能方程各项进行机理分析,解释了亚临界圆柱绕流工况下几种LES 模型和实验数据在回流区长度和尾迹区平均速度两个方面上产生差异的原因.国内学者贾宏涛等[12]利用子波分析在壁湍流流向和展向上分别进行多尺度分解,发现流向主要以反传为主,而展向存在明显正传,当截断尺度增大时则以正传为主.王占莹[13]采用临界点理论的流型分析方法发现对数区能量正传事件与不稳定的结点/鞍点密切相关,而反传事件中稳定的焦点占比最大.实验方面,Natrajan 等[14]通过对平板边界层PIV 实验数据在物理空间进行滤波,发现在对数层中,瞬时正传事件发生在上抛事件附近,两个相邻的发卡涡头之间,而最强烈的正传事件则出现在下扫事件附近,并形成沿着发卡涡背部的倾斜剪切层.相反,局部的反传事件则出现在发卡涡头部与流向方向相反的上方和沿流向方向的下方,后者要比前者更强烈.最后,在涡包的尾迹边缘经常能观察到显著的瞬时能量反传事件.王帅杰等[17]通过使用压电陶瓷振子在平板壁面展向施加不同频率振幅的周期性扰动,表明壁面周期扰动可通过使大尺度扫掠流体破碎为小尺度结构达到减阻效果.此前的结果在一定程度上对能量传输性质特别是与近壁区相干结构有关的特定区域的传输性质进行了刻画,然而这些研究往往只关注了特定区域或特定条件的传输事件,而忽略了部分传输区域和事件的存在,缺乏对传输事件的全面统计,随着新的流场结构识别技术的提出[21-29],对瞬时三维流场内结构的全面统计已成为可能.Del ´Alamo 等[21]采用聚类分析方法(clustering methodology)统计了壁湍流涡团结构的性质,发现按照距壁面距离可将涡团分为附着族类和分离族类,其中附着部分为一类尺寸自相似族群,而分离结构的尺寸仅与当地Kolmogorov 尺度有关.Lozano-Dur´an 等[22]采用聚类方法对壁湍流上抛下扫结构中的附着结构和分离结构的分布特性和几何特性进行了全面而精确的刻画,进一步采用直接数值模拟时间解析数据,对结构的分裂、融合等演化形为进行了定量刻画.Cheng 等[25]采用聚类方法,在中低雷诺数下通过对脉动速度结构的统计对壁湍流前沿的附着涡理论进行了解释.Dong 等[28]则采用聚类方法给出了均匀剪切湍流中能量级串结构的空间结构统计特性并采用条件统计研究了正反级串结构的形成机理.将瞬时流场内发生能量正传和反传的区域定义为级串结构,本文采用空间滤波方法(filterspace technique)获取不同尺度间的能量传递,结合聚类分析法对流场内的级串结构进行了进一步的刻画,由于本研究所考虑的问题需在均匀网格数据下进行分析,所以本文采用格子玻尔兹曼方法(lattice Boltzmann method,LBM)进行模拟,LBM 在本研究中的优势在于无需对后处理数据额外插值,实现简单,易于并行.本文的主要内容如下:第1 部分首先介绍了LBM 的基本方程、外力项及边界条件等的处理,结合空间滤波方法给出了表征跨尺度能量传递的物理量,最后介绍结构识别捕捉方法—聚类分析方法.第2 部分介绍了直接数值模拟的参数设置.第3 部分给出了本文的数值模拟结果与已有的DNS 结果对比,进一步的给出了滤波场的统计结果,均与前人的统计结果一致,证明了数据和滤波方法的可靠性.最后给出了聚类分析方法的得到的结构统计结果.

1 数学模型

1.1 基本控制方程

格子Boltzmann 方程是Boltzmann-BGK 方程的一种特殊离散形式,这一离散包括速度离散、时间离散和空间离散.Boltzmann 方程描述了离散粒子分布函数的演化,以f(x,t,ζ)代表特定时刻t,特定位置x处,速度为ζ 的粒子密度分布函数.进一步将Boltzmann 方程在时间和空间离散,将空间中有无穷方向可能的速度离散为时间步Δt内空间格子中有限方向的速度集合ci,在离散时间步Δt内粒子仅在格子内运动,由此导出的格子Boltzmann 方程为

在SRT-LBM 算法中,计算通过碰撞、迁移两步来执行.首先,经过碰撞的粒子由非平衡态向平衡态趋近,此过程称为驰豫.紧接着,粒子的分布函数fi随着粒子按照对应的格子速度ci和权系数ωi迁移到相邻格点上.

考虑外力项的处理,本研究采用直接在演化方程中增加一个作用力项来实现体积力F在LBE 中的影响[31],即

其中,Fi进一步通过基于格子气自动机方法中处理作用力的方法[32],将Fi表示为

对于边界条件,本研究采用郭照立等[30]提出的非平衡外推方法,将边界格点处的未知分布函数分解为平衡态和非平衡态两部分,即

1.2 跨尺度能量传递

在大涡模拟理论中,基于滤波操作,Navier-Stokes方程中的独立变量被划分格子尺度和亚格子尺度(SGS)两部分,本研究中采用的是物理空间中的各向同性高斯滤波器直接对DNS 数据进行低通滤波,在尺度l上进行的滤波函数记为Gl(x),则滤波操作如式(1)

对连续性方程和NS 方程进行滤波得

其中,方程等号左边第1 项为对流项,等号右侧第1～6 分别对应湍流输运项、压力扩散项、黏性扩散项、亚格子应力扩散项、黏性耗散项和能量通量项.亚格子应力耗散项代表解析尺度和未解析尺度之间的净能量交换,为大尺度应变率张量,定义Π 为尺度间能量交换的度量,Π 值为正代表能量从解析尺度向过滤尺度传递,Π 值为负代表能量从过滤尺度向解析尺度反传

1.3 空间强结构捕捉——cluster 方法

对于任意时刻流场内不同湍流结构总是通过若干等值面互相黏连,这对使用数字手段区分不同结构造成了干扰,因而需要某种手段人为地去除这些黏连的部分,基于这种思想,Moisy 等[20]率先通过筛选出瞬时流场内大于自身a倍的标准差的数据点,由此保留了瞬时流场内在长时间统计上表现较为强烈(intense)的点,筛选掉的即为瞬时流场中的不同结构之间的黏连部分,这种方法称为聚类分析方法.本研究采用cluster 方法来识别近壁区中的发生跨尺度能量传递的区域所包围的结构,结构由满足下列条件的空间联通区域确定

其中Πrms为Π(x,y,z)的标准差,α 为需经逾渗分析(percolation analysis)所人为选定的阈值.结构的连通性由笛卡尔网格中满足六正交相邻条件所确定,如图1 所示.

图1 六联通示意图Fig.1 Six-connected pixels

通过式(22)可将结构分为正级串Π+和逆级串Π-结构,进一步构建出每个结构的轴对齐最小包围盒(axially aligned bounding box),以边界框的长lx,宽lz,高ly分别代表结构沿流向、展向和垂向的尺寸.

2 模拟参数设置

2.1 模型参数

对于槽道湍流,除雷诺数外,首先应确定模拟所需要的计算域尺寸.Jimenez 等[32]研究了能够维持湍流所需要的最小槽道尺寸,他们定义αx=Lx/H,αz=Lz/H,基于此Spasov 等[33]使用LBM 模拟Rτ=180 的槽道湍流时取αx=4,αz=1,结果与Kim 等[34]的研究相比,平均速度剖面结果基本吻合但在对数区略高,雷诺应力的结果也存在一定偏差,因此本研究选取的槽道尺寸为αx=4.6,αz=2,网格数Lx×Ly×Lz为600×260×260.槽道尺寸选定后,对于直接数值模拟,每个网格的尺寸都应小于当地的Kolmogorov 尺度η.对于槽道湍流在垂向方向上壁面处耗散率最大,相应的当地Kolmogorov 尺度η 为需要解析的最小尺度,定义壁面处Kolmogorov 的尺度为η0,考虑

由Kim 等[34]提供的数据可知,的最大值约为0.2,相应的=1.5.由于LBM 中网格尺寸为无量纲数Δ=1.

对于摩擦雷诺数Reτ=uτH/ν=180,槽道半高须满足H≥120,在本研究中取H=130.

摩擦速度可由对数律公式估计

其中κ 为卡门常数,约等于0.4,B取6.对于LBM,为了满足低马赫数条件,流场中的最大速度须小于等于0.1[33],对于槽道湍流最大平均速度在槽道中心,所以可取U0=0.1.

由此,黏性系数和压力梯度分别为

3 结果与讨论

3.1 数值模拟验证

图2 为基于Q准则的空间涡结构等值面图,=0.015,展示了流场内涡结构的分布,从图2 可以看到近壁区的准流向涡和一些类似发卡涡的结构.图3 为平均速度U+沿垂向变化曲线,符号圆点为本文DNS 的结果,虚线为Kim 等[34]的结果,叉型标记为Lee 等[35]的结果,可以看到,本文的平均速度剖面结果与Kim 等[34]吻合得较好.此前本研究也计算过αx=4,αz=1 的结果,结果显示在对数区吻合的效果并不理想,这与Spasov等[33]和许丁等[36]的结果类似,表明展向尺寸也会对计算结果产生显著影响.

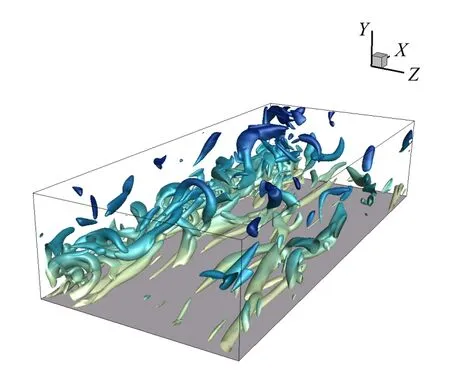
图2 基于Q 准则槽道下半部涡结构等值面图Fig.2 Iso-surface of Q on the lower-half of the channel

图3 平均速度剖面Fig.3 Comparison of mean streamwise velocity

图4 和图5 为湍流统计量脉动速度均方根和雷诺应力的统计结果,与Kim 等[34]和Lee 等[35]Reτ=180 下的DNS 结果对比吻合得较好,同样在αx=4,αz=1 的条件下,结果也存在较大偏差.

图4 脉动速度均方根沿法向变化曲Fig.4 Comparison of r.m.s.of velocity fluctuations

图5 雷诺应力沿法向变化曲线Fig.5 Comparison of Reynolds shear stress

3.2 尺度间能量传递结果统计

图6 展示了4 种滤波尺度下的级串结构等值面图,等值面的取值分别为:±3.16×10-7,±3.3×10-7,±5.0×10-7,±1.83×10-9,其中乳白色等值面为负的逆级串结构,即能量从小尺度相大尺度传递,(a,b,c,d)中的其他颜色分别为蓝色、绿色、橙色、紫色,均代表取值为正的正级串结构,即能量从大尺度向小尺度传递.

图6 四种滤波尺度下的级串结构等值面图Fig.6 Interscale energy transfer stucture at four different scale

可以看到近壁区依附有很多体积较大的长条带结构,这与近壁区拟流向涡的形态比较相似,且正负级串沿展向交替排列,而小体积结构多存在于远离壁面的层级中.图7 展示了时间平均后的亚格子耗散项沿垂向的分布情况,滤波尺度为23η0,趋势上与Piomelli 等[8]采用盒式滤波器的结果一致,结果表明反级串结构效应尽管弱于正级串,但仍然较为显著.正反级串效应在缓冲层内达到峰值,正级串总体上强于反级串,在缓冲层内二者的差值达到最大,缓冲层后二者大致相当.

图7 能量通量沿法向分布Fig.7 SGS dissipation in the normal direction

图8 展示了亚格子应力耗散项的概率密度分布,与Piomell 等[8]、Natrajan 等[15]的结果一致.结果显示正级串的概率密度较反级串更大,正级串横轴尾部也较长,说明正级串效应较反级串效应略强,但反级串效应也较为显著.

图8 能量通量概率密度分布Fig.8 Probability density function of energy flux

3.3 能量级串结构的空间统计

应用cluster 方法首先要进行逾渗分析(percolation analysis)[21-22]选定某一阈值,当阈值较低时,新的结构点被识别出,并与已识别的结构体融合,如果阈值为零,所有的结构将会融合成少量的复杂结构,从而对结构研究造成干扰,而阈值过大又会造成筛选掉过多的结构,这里采用Jimenez 等[21-22]所采用的方法来尽可能地使用较小的阈值使得结构仍能被单独识别出来.图9 展示了不同α 值下最大cluster结构的体积与所有cluster 结构体积之和的比值以及不同α 值对应的cluster 结构数量N与所有α 值能识别出的最多数量Nm的比值.由图9 可以看出,当α较小时,大部分结构融合在一起,仅有少量的结构被识别出,随着α 的增大,结构逐渐“断裂”,新的结构从原有结构脱离出来,在α=1 处,3 种滤波尺度的结构数量均达到峰值附近,此时解析的数量较高,对应的体积曲线位于中段,α 值的选择是“断裂”和“融合”两个过程相平衡的结果.图9 所展示的变化趋势与Jimenez 等[21-22]的研究中涉及的湍流结构所体现的规律相一致,Jimenez 等[20]将结构的这种特性称为“渗透性”.基于图9 的结果,取阈值α=1.

图9 结构的逾渗分析Fig.9 Percolation analysis of the identified clusters

图10 为级串结构体积的统计结果,可以看到小尺寸结构出现的概率要远远高于大尺寸结构,且体积概率密度分布呈现-4/5 的幂律关系.图11 展示了槽道内能流结构数密度随结构距壁面的最小距离ymin和距壁面最大距离ymax的分布规律.从图11 可以看出,结构主要集中在以=17 为分界线的两侧,因此可将能流结构划分为<17 的壁面附着结构,以及>17 的分离结构.这个分界线的距离与Lozano-Dur´an 等[22]研究中所涉及的上抛下扫结构的分界线y+=20 十分接近,表明两种结构的分布可能存在某种关联.

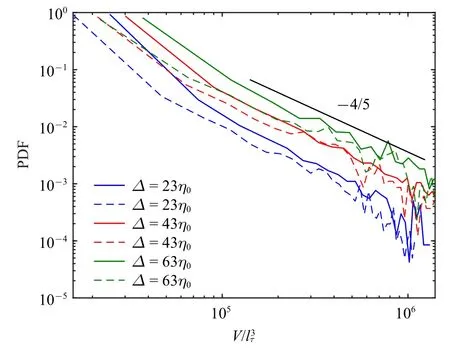
图10 级串结构体积概率密度分布Fig.10 Probability density function of volume of structure

图11 结构按距壁面最小距离和最大距离的二维分布Fig.11 The number of the clusters per unit wall-parallel area as a function of ymin and ymax

表1 进一步给出了附着结构和分离结构的数量占比和体积占比.可以看到,Π+附着结构的数量只占结构总数的18%,但体积分数却占到69%,而对应的分离结构数量占比和体积占比分别为82%和31%.Π-附着结构的数量占比仅为14%,体积占比却达到了60.5%,相应的分离结构分别占比86%和39.5%.这说明无论是Π+还是Π-结构,大尺寸结构都主要分布在附着结构中,而分离结构中主要为小尺寸结构.

表1 正反级串结构的数量占比和体积分数Table 1 Number and volume fractions with respect to the total number and total volume of all the structure

其中为单个结构的几何中心,d(i) 为包围盒对角线长度.采取与Lozano 等[22]类似的配对方法,只考虑包围盒对角线长度之比满足1/2 ≤d(j)/d(i) ≤2,且距离最近的正级串附着结构和反级串附着结构为一对结构对.图13 给出了流向相对距离δx和展向相对距离δz的二维散点图.由图13 可见二维散点主要分布在δy=0 两侧,而在δz=0 附近的散点极为稀疏,这说明结构对在展向上总是保持一定距离,几乎不会在展向发生重叠,表明附着结构对更倾向于沿展向并排排列.

图12 (a)(b)Π+ 结构流向长度、展向长度与纵向长度的联合概率密度;(c)(d)Π- 结构流向长度、展向长度与纵向长度的联合概率密度Fig.12 (a)(b)Joint p.d.f.s of the length()and widthof with respect to their height();(c)(d)Joint p.d.f.s of the length()andwidth()of with respect to their height()

图13 能量级串结构对流向相对距离与展向相对距离的二维散点图Fig.13 Scatter of the relative distance between Π+ and Π- structure pairs in the streamwise direction and spanwise direction

4 结论

本文通过LBM 方法得到直接数值模拟数据与已有槽道湍流数据库对比,结果吻合较好.通过各向同性高斯滤波器对数据进行滤波构建表征可解尺度与亚格子尺度之间能量交换的物理量,表明正级串出现的概率要大于逆级串,且正反级串均在缓冲层内达到峰值.对级串结构使用cluster 方法进行空间统计表明:以结构包围盒下方距壁面距离y+=17 为分界,结构集中分布于分界线的两侧,即距壁面距离小于y+=17 的附着结构,和距壁面距离大于y+=17的分离结构.对附着结构进一步统计表明:级串结构的流向长度和展向长度均与纵向长度满足特定的幂律关系,即结构在尺寸上存在着自相似性.最后对满足尺寸相近且距离最近的正反级串附着结构对的流向与展向相对距离的统计表明,正反级串附着结构更倾向于沿着展向并排排列.