精确计算弹性薄型结构中奇异积分方法

郭壮志

（1.郑州轻工业大学机电工程学院,河南 郑州 450002；2.河南省机械装备智能制造重点实验室,河南 郑州 450002）

在弹性问题的边界元法求解中，弱奇异积分一直是其研究的一个重要课题[1-4]。尤其对于薄型结构[5-8]，此结构在进行离散时，将会存在形状较差的单元（比如含大角度或狭长的单元），严重影响计算结果的精度。准确快速的计算边界积分方程中的弱奇异积分是其顺利求解的关键。

目前有很多处理弱奇异积分的方案，比如积分简化法、单元细分法和坐标变换法等[9-12]，每一种方法都存在优缺点。但当源点位置比较差时（比如源点靠近单元的边界），单纯的积分变换无法获得较高的计算精度，需要对单元进行细分。因此，单元细分法加上极坐标变换方法是最广泛应用的一种方法。目前存在不少的细分方法，比如奇异点（即源点）直接和单元顶点相连、区间分块法，等等，这些方法在进行细分的时候，会分出一些形状比较差的积分块（比如含大角度的三角形积分块和边长比较大的积分块），为奇异积分的处理增加了困难。极坐标变换法是消除弱奇异性的关键，它把面积分转换为环向和径向的双重积分，再对径向作变换来达到消除奇异性的目的。但这种方法在使用时，每次都需要重新计算积分块在径向和环向的积分区间，实现起来比较的麻烦。

本文针对弹性薄型问题边界积分方程中位移基本解的弱奇异性质，对于一个离散单元的数值积分，首先依据源点位置、单元形状和源点到单元的最近距离，分别开发三角形和四边形单元的细分技术；然后在该细分技术的基础上，针对细分所得到的积分块，构造一种更加简单的坐标变换法，用来消除被积函数中的奇异性。该方法相比常规的极坐标变换法，不需要再去计算它们的积分区间，实现起来更加简单有效；最后将该细分技术和坐标变换方法用于弹性薄板结构的边界元法求解，实现该问题精确有效的求解。

1 薄型问题的奇异边界积分方程

三维弹性薄型问题的边界积分方程如式（1）所示，其中P和Q分别为源点和场点，在光滑边界上cij(P)=0.5，和为位移和面力基本解，其表达式如式（2）所示。

其中，G和v分别是剪切模量和泊松比，r是源点和场点之间的距离，uj(Q)和tj(Q)分别表示边界上的位移和面力，δij为克罗内克符号，ni和nj为i、j方向的外法向量。若把方程(1)中的边界离散成N个单元，式（1）可以写为：

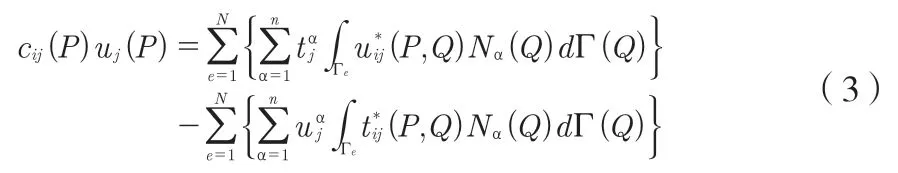
其中，n是每一个单元上的节点数，Nα(Q)是单元上第α个节点的形函数。从式(2)可以看出，对位移基本解的积分具有弱奇异性，而对面力基本解的积分具有强奇异性，本文重点关注对位移基本解的积分。

2 弱奇异边界积分处理方法

首先取一个离散单元作为研究对象，把对位移基本解的积分简化成式（4）形式，其中，P和Q分别代表着源点和场点，r是P和Q之间的距离，f(P,Q)为是一个不带奇异性的光滑函数，Ф(Q)是相应的形函数。

针对此离散单元的积分具有弱奇异性，下面介绍一下对该单元的奇异积分处理方法，以达到精确求解弱奇异积分的目的。先来介绍一种奇异积分单元细分技术。

2.1 求解奇异积分的单元细分技术

由于源点位置的不确定性（可能落在单元的内部、边和顶点上），所以细分方式也会不同。当源点位置给定时，首先计算源点到单元各边的最近距离d，然后以0.2 d为长度在源点附近构造一个很小的四边形，并把源点包括在里面。再分别延长小四边形的四条边，分别与积分单元进行相交，得到若干个三角形和四边形积分块。最后把包含源点的小四边形的各个顶点与源点相连得到若干个含奇异点s的三角形积分块。三角形和四边形单元的具体细分方案如图1和图2所示。其中，0.2 d的选取是为了避免积分块之间相互干涉，根据数值试验得到的一个经验数值。

图1 不同源点位置三角形单元的细分方法

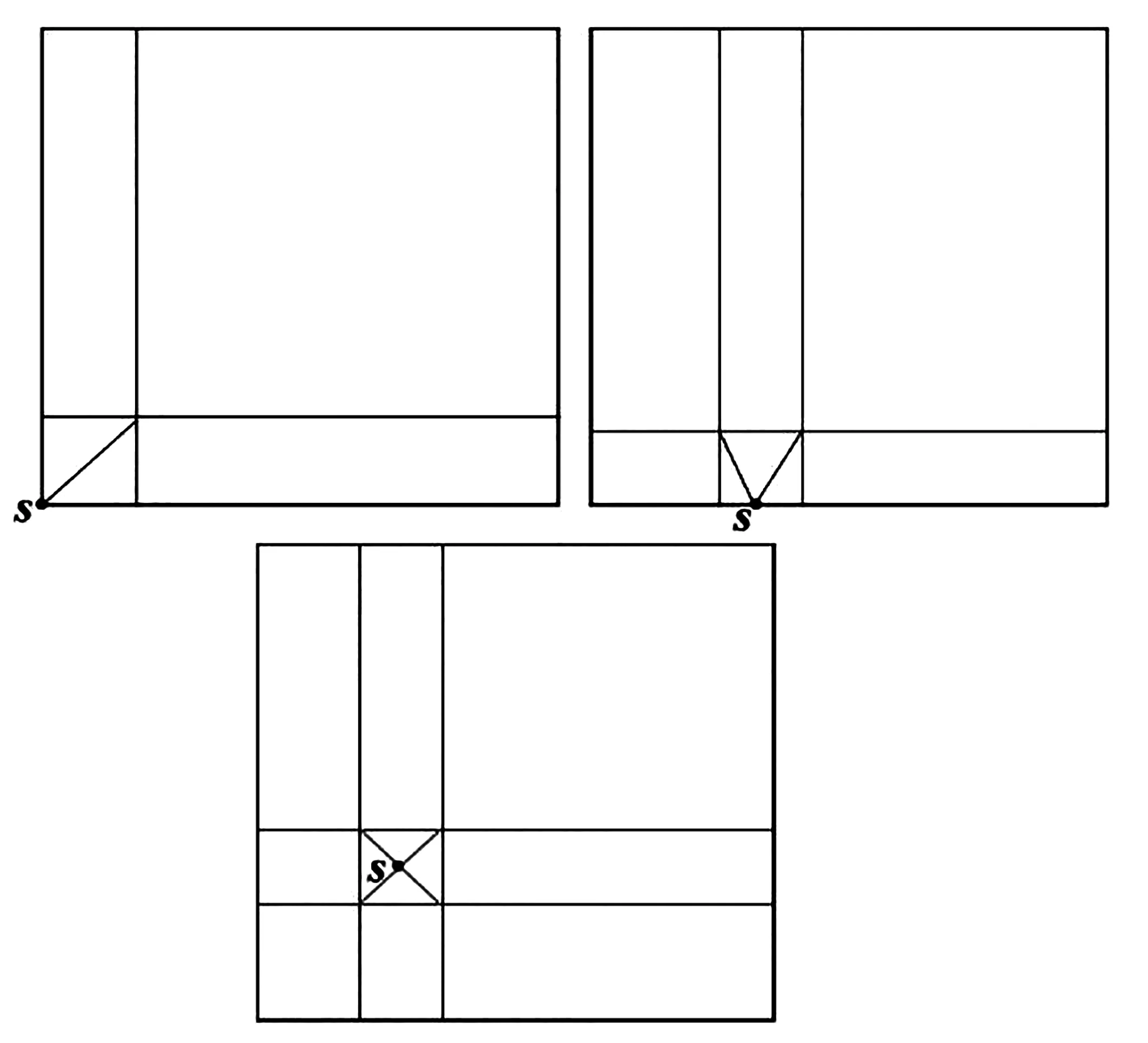
图2 不同源点位置四边形单元的细分方法

除此之外，若积分单元比较狭长，可以先根据该单元的最长(Lmax)和最短边(Lmin)的比例先对其进行一次细分（如图3所示，若Lmax/Lmin＜ 2则不分；若2 ＜Lmax/Lmin＜ 3，就把该单元分成两个积分块。以此类推），然后按照图1和2中的细分方式对含源点的积分块进一步细分。另外，若细分得到细长的积分块（图1和2中细长的四边形积分块），仍可根据图3中的方法，对该积分块进一步细分，以确保细分结果中不出现含较大边长比的积分块。

图3 细长四边形单元的细分方法

2.2 弱奇异性消除方法

通过上述单元细分可知，不管是三角形还是四边形单元，最后都会把包含奇异点（源点）的小四边形分成若干个三角形，而源点刚好是这些三角形的其中一个顶点。不含源点的积分块可以通过普通的高斯积分（四边形积分块）或汉默积分（三角形积分块）来求解，但由于包含源点的三角形积分块具有奇异性，单纯的汉默积分无法消除被积函数中的奇异性，需要进行特殊处理。

以式(4)作为积分方程，针对细分得到的包含源点的积分块，本文构造一种新型的坐标变换法来消除其奇异性。引入了(α,β)局部坐标系，相应的坐标变换如图4所示。

图4 三角形积分块的坐标变换

坐标变换的具体过程如下：

将式（5）和（6）代入（7）可得

通过式（8）的坐标变换，把原自然坐标系下的三角形映射为局部坐标系下的一个正四边形，四边形的两个顶点坐标分别为（0，0）和（1，1），即局部坐标α和β的取值范围为[0,1]。坐标变换的雅可比为αS。

经过变换之后，式（4）在奇异三角形积分块的积分就可以写成如下形式：

从式（5）～式（9）可以看出，这种新型的坐标变换得到的雅可比中含有拟零因子α，刚好和积分方程（4）分母中的拟零因子抵消掉，达到消除奇异性的目的。并且这种坐标变换方法直接把α和β的积分区间变换到[0,1]，不需要再去计算每一个积分块的积分区间，相比传统的极坐标变换实现起来更加的简单有效。

3 数值算例

本节给出了几个算例来验证本文方法的精确性和有效性。首先验证本文方法在一个单元上的积分精度（算例考虑了不同源点位置和单元的形状类型），最后把本文方法用于弹性薄板结构的求解。相对误差的计算式如式(12)所示。

其中，In为数值计算结果，Ie为相应的参考解。参考解通过使用单元细分和坐标变换法，采用大量高斯积分点得到。为了方便计算，假设在式(4)中，f(P,Q)=1.0。下述第一个例子考虑式（4）形式具有弱奇异性的边界积分。

3.1 奇异积分算例

本例以四边形单元为例来验证本文方法。四边形单元的四个顶点为(0.0,0.0,0.0)、(1.0,0.0,0.0)、(1.0,1.0,0.0)和(0.0,1.0,0.0)，边长比为a=1。采用本文方法和传统方法（坐标变换加传统单元细分法，其中传统单元细分法是源点直接和单元顶点相连），得到的数值结果如表1所示。

当四边形单元的边长比为5时，给定4个顶点为(0.0,0.0,0.0)、(5.0,0.0,0.0)、(5.0,1.0,0.0)和(0.0,1.0,0.0)，计算结果如表2所示。

表2 四边形单元奇异积分数值结果（边长比5:1）

当四边形单元的边长比为10时，给定4个顶点为(0.0,0.0,0.0)、(10.0,0.0,0.0)、(10.0,1.0,0.0)和(0.0,1.0,0.0)，计算结果如表3所示。

从表1～表3可以看出，在高斯点数相当的前提下，随着积分单元边长比的增加（即单元变得狭长），本文方法的计算精度一直保持较高。

表1 四边形单元奇异积分数值结果（边长比1:1）

表3 四边形单元奇异积分数值结果（边长比10:1）

3.2 薄型平板结构

把本文方法应用到弹性薄板结构的边界元法求解中，考虑图5这样一个薄板，长宽高分别为l=10 mm，l=10 mm，h=1 mm。统一量纲下弹性模量和泊松比分别为E=1 Mpa，v=0.25，质量密度为ρ=1.14。为了方便对比，在薄板边界上施加具有解析解的二次位移场，表达式如式(13)所示。

图5 薄板模型

把薄板模型离散成140个四边形单元，侧面用细长的四边形单元进行离散。在x=10、z=0.5这条线上选择一系列样本点，采用本文方法和传统方法的计算结果如图6和图7所示。

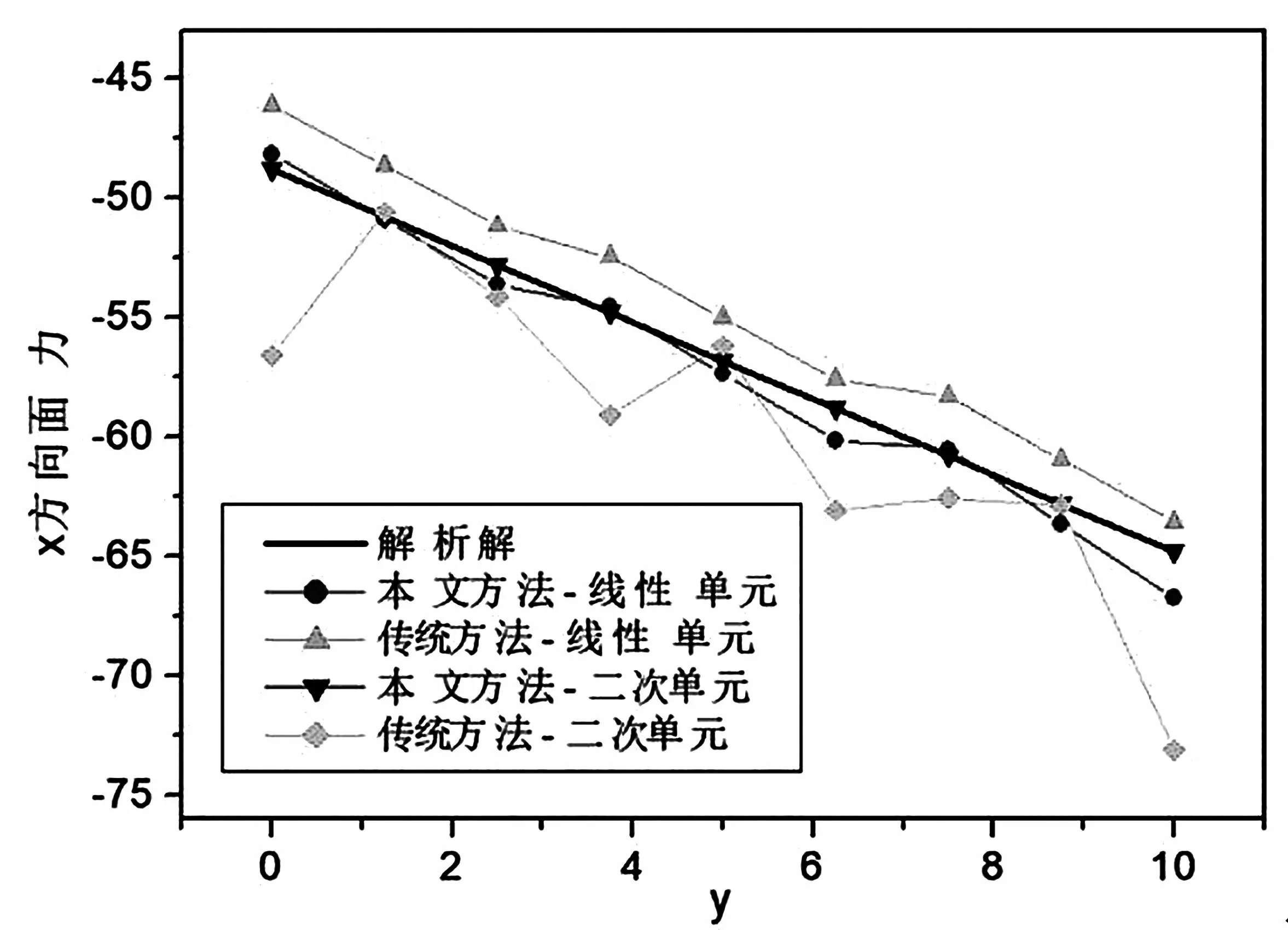
图6 x方向的面力结果

图7 米塞斯应力结果

由此看出，相比传统方法（坐标变换加上传统单元细分法，其中单元细分法是源点直接和单元顶点相连接的方法），本文方法的计算结果和解析解吻合得更好，精度更高，进一步验证了本文方法的精确性和有效性。

4 结论

本文从弹性薄型问题边界积分方程中存在的弱奇异积分的性质出发，提出了一种单元细分结合坐标变换的方法。该方法实现起来更加简单，无论源点在单元的什么位置，无论单元形状怎样，都可以得到精确稳定的计算结果。然后通过C++编程软件，结合UG建模和仿真平台实现本文方法，并将其应用到薄板结构的边界元法求解中，获得了较好的计算结果，进一步验证了本文方法的精确性和有效性。