复杂型面点云的法向特征聚类分级估计方法

孙殿柱,沈江华,汪思腾,李延瑞,林 伟

(1.山东理工大学 机械工程学院,山东 淄博 255049；2.西安交通大学 机械工程学院，陕西 西安 710049)

0 引言

点云的法向信息是三维模型不可或缺的属性，法向估计的准确性和一致性直接影响点云配准[1-2]、精简[3-4]和曲面重建[5-6]等后期处理的准确性。随着点云数据在逆向工程、工业制造及医学可视化等领域的应用，复杂型面采样点云，特别是含棱边特征点云法向估计的精确度问题一直倍受关注[7-8]。

目前，应用最广泛的法向估计算法为Hoppe等[9]提出的点云微切平面估计法，其主要思想是用样点的k-邻域计算其最小二乘意义上的局部拟合平面，将拟合平面的法向作为点云的法向。为进一步提高法向估计的准确性，Pauly等[10]在其提出的散乱点云曲面建模中，采用移动最小二乘表面定义中的局部参考平面估计样点的法向；Gross等[11]为样点的邻域点集赋予高斯权重，使距离样点越近的邻域点对法向估计的影响越大，距离越远的邻域点影响越小；Yoon等[12]对样本进行多次随机采样得到若干个相互覆盖的子集，将基于各子集估算的样点法向均值作为样点的最终法向。然而，因为点云微切平面估计法及其改进算法均将欧氏距离搜索的样本作为平面拟合数据，所以在后期处理的曲面重建过程会将尖锐特征平滑掉，为提高棱边尖锐特征区域点云法向估计的准确性，王醒策等[13]通过Hoppe算法获取初始法向，然后改进移动最小二乘曲面重建算法实现局部曲面拟合，以重建的网格面片作为样点法向；孙殿柱等[14]提出一种以有界泊松曲面逼近局部样本作为约束的样点法向加权估计算法，通过泊松曲面逼近样本点，用有界泊松曲面离散网格中距样点最近的网格面片作为样点的参考面片，并基于顶点邻域面的正则度及邻域面到该顶点的测地距离估计参考面片顶点法向，将参考面片各顶点法向的加权求和结果作为样点最终法向；Mura等[15]对样点局部邻域进行离散化，选择距邻域中心最近的样点，以其法向修正初始经由Hoppe算法估计的法向；Cao等[16]通过最大化邻域结构一致性对局部样本进行漂移获取样点的各向同性邻域，可提高棱边样点邻域样本搜索的准确性，避免棱边区域样点法向被平滑处理。

现有的点云法向估计算法对实物表面采样数据所作的主要假设是数据来自光滑曲面，即任一样点的欧氏近邻点集构成的曲面样本所呈现的形貌近似平面，这一假设对含有棱边(或小半径圆角)和尖角等特征的曲面样本无效。在工业设计领域，有许多产品的数字模型是基于曲面求交、裁剪、倒角等建模过程构造的复合曲面模型，对于该类产品的实物表面采样数据，在特征区域，若将曲面局部样本所体现的形貌视为平面，则将导致样点的法向和曲率等微分几何量的估计结果与真实情况存在较大偏差。

针对上述问题，本文提出一种基于曲面形貌聚类优化的点云法向估计方法。首先，基于曲面局部平坦性和贝叶斯信息准则对每个样点邻域构成的曲面局部样本进行聚类分析，将曲面采样点云划分为平坦区域、特征边缘、棱边区域和尖角区域等类别；然后，估计平坦区域样点的法向，以该类样点的法向作为确定性最高的初始法向；最后，将平坦区域样点法向向邻近特征区域样点分级传播，实现特征样点的法向估计。本文方法对复杂型面样点的分类与曲面形貌一致，可有效提高特征边缘样点法向估计结果的准确性，并能保证棱边和尖角区域样点法向具有多义性。

1 曲面样本分类

设S为曲面采样点云，对于任一样点p∈S，可基于S的空间索引(kd树、空间八叉树或R树皆可)[17]从S中搜索距离p最近的k个样点，并将其与p所构成的点集作为以p为中心的曲面局部样本λ(p)。

若S来自光滑曲面，则可采用平面逼近λ(p)的方法估计p的法向，然而对于形貌复杂的曲面采样点云，如图1所示的涡轮发动机轮盘点云，在棱边特征区域，λ(p)包含来自两张曲面的样点，亦即在理论上p有两个法向，仅以单张平面逼近λ(p)来估计p的法向会导致错误的结果。含有小圆角特征的曲面局部样本也存在类似问题。因此，为提高复杂型面采样点云法向估计结果的准确性，必须对样点所处区域对应的曲面特征进行识别和分类，然后针对特定类别对样点的法向估计结果进行优化。

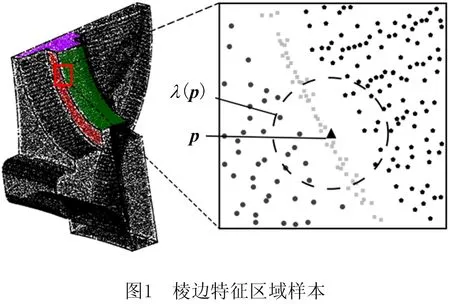
复杂型面的形貌复杂性可基于曲面上任意一点的曲率作量化分析，然而对曲面采样点云而言，其中任一样点与其周围样点不存在任何拓扑和几何意义上的邻接关系。对曲面采样点云S中的任一样点p所处区域对应的曲面特征进行识别和分类的前提是，为λ(p)的形貌复杂性构造与曲面形貌一致的量化模型。

复杂型面上的棱边和尖角等特征区域有别于平坦区域，对于后者，可基于λ(p)拟合平面γ(p)，用λ(p)中的样点到γ(p)的残差衡量λ(p)形貌的平坦程度。设λ(p)中所有样点到γ(p)的残差平方和为χ(p)，用阈值ε区分λ(p)的形貌是否平坦，若χ(p)≤ε，则λ(p)形貌为平坦；若χ(p)>ε，则为不平坦，将λ(p)视为处于小圆角、棱边或尖角等特征区域。因此，基于ε可实现对曲面采样点云S中平坦区域样点与非平坦区域样点的分离，设结果分别为S1和S2。为便于描述，将χ(p)称为λ(p)的形貌特征值。

对于p∈S2，可继续基于ε对其所处特征区进行细化识别。假设p处于棱边区域，若将λ(p)中所有形貌特征值大于ε的样点全部剔除，则可得点集λ′(p)。若λ′(p)非空，则因λ(p)中被剔除的样点集中于曲面的棱边区域，而且λ′(p)中的样点主要分布于棱边区域两侧的平坦区域，所以在欧氏空间中只需对λ′(p)进行聚类划分，便可分离不同平坦区域的样点，如图2所示。若λ′(p)被划分为两类，则认为p处于棱边区域；同理，若划分结果多于两类，则可认为p处于尖角区域。关键问题在于，如何确定λ′(p)聚类划分结果的数量。

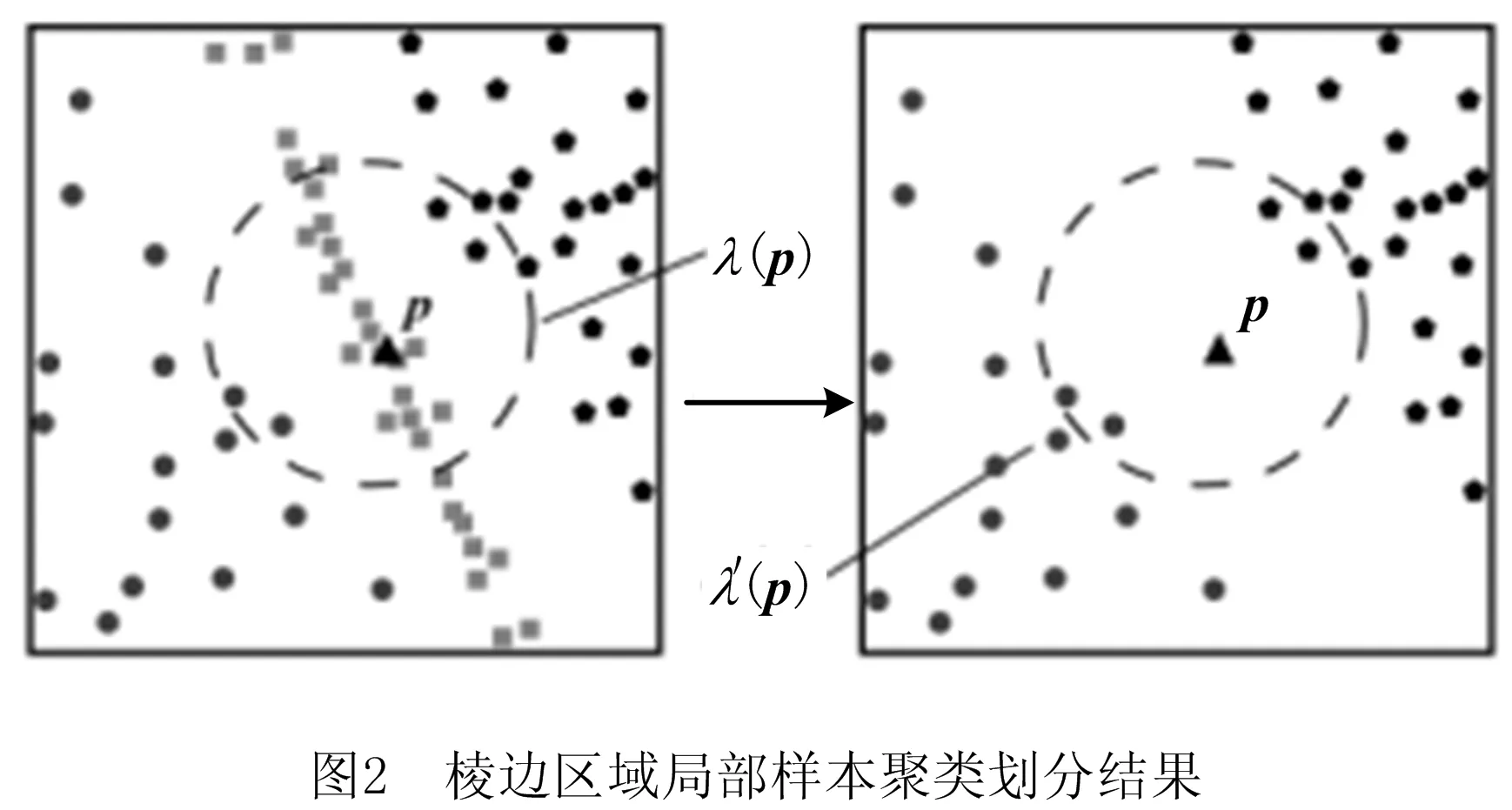
假设λ′(p)的聚类结果为C={C1,C2,…,Cm}，m值取决于C的聚类最优性。若采用k均值聚类算法[18]对λ′(p)进行划分，则可基于贝叶斯信息准则(Bayesian Information Criterion，BIC)[19]估计C的聚类优性。对于λ′(p)任一候选的聚类划分结果Ci={Ci1,Ci2,…,Cim}，其聚类优性可量化为

B(Ci)=2logL(mi|Ci)-dlog|λ′(p)|。

(1)

式中：L(mi|Ci)为似然函数；d为样点数据维度(文中d=3)；|λ′(p)|为λ′(p)包含样点的个数。定义

(2)

2 特征样点法向估计

若样点p处于曲面平坦区域，即χ(p)≤ε，则γ(p)的法向便可作为p的法向估计结果。值得探讨的是，当p处于曲面上的特征区域时，其法向如何确定。

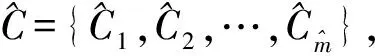
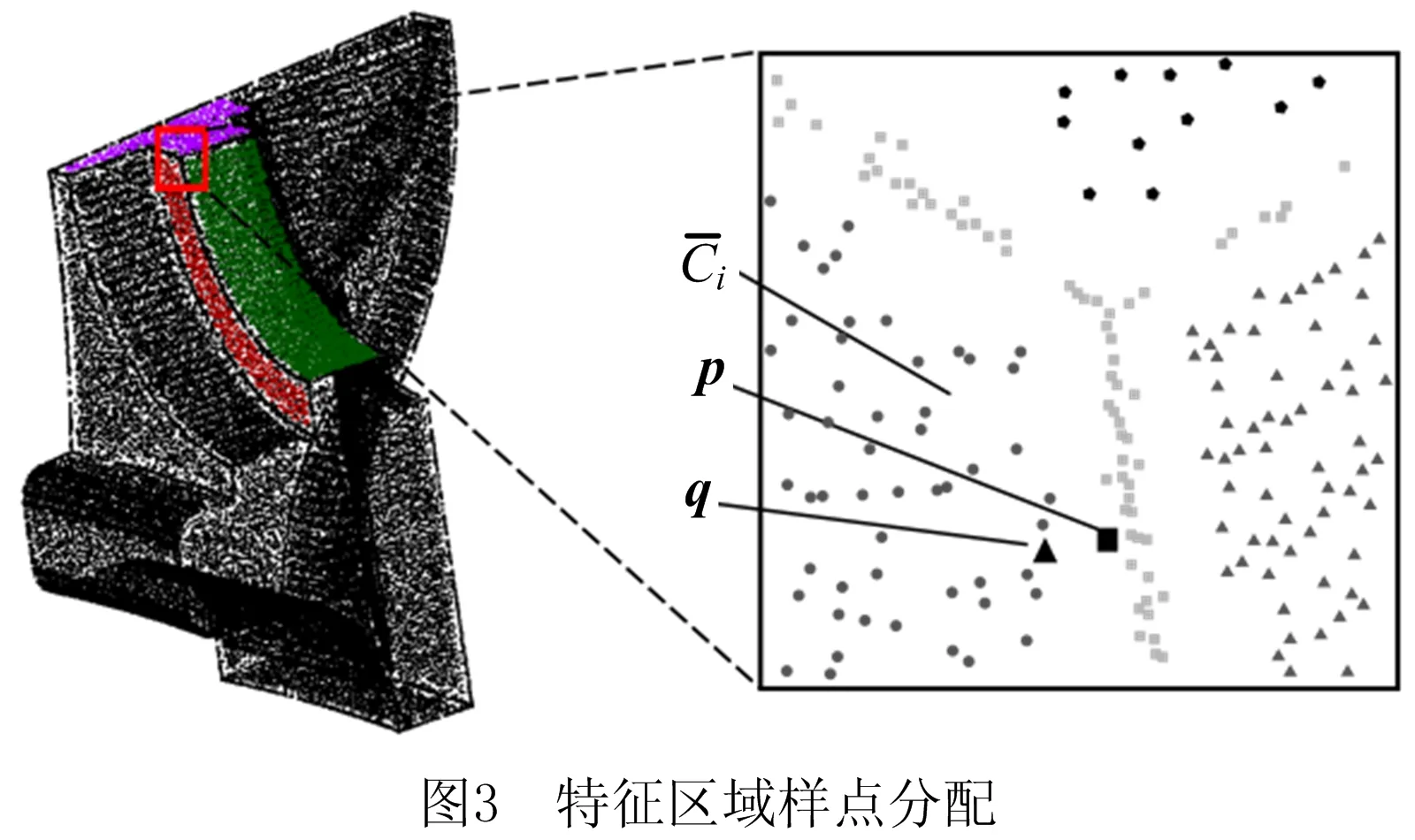
基于上述分析，设曲面采样点云S中法向确定的样点所构成的集合为P={p1,p2,…,pn}，将特征边缘样点、棱边区域样点、尖角区域样点分别赋以级别编号1，2，3，则样点法向确定性的传播过程如下：

(1)h←1。

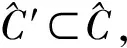
(4)从P中剔除pi。

(5)重复(2)～(4)，直到P中不存在级别为h的样点。

(6)h←h+1。

(7)重复上述步骤，直到P为空集。

对于棱边区域或尖角区域的任一样点，上述过程为其估计的法向并不唯一，每个棱边区域样点有两个法向，每个尖角区域样点有3个甚至更多法向，这种结果与曲面棱边和尖角特征相符，即棱边为两张光滑曲面的交线，而尖角为多张光滑曲面的交点，因此棱边样点和尖角样点的法向必定具有多义性。现有的曲面采样点云法向估计算法通常忽视了该性质，为棱边区域和尖角区域样点所估计的法向通常近似为多义性法向的合向量，这种单一的法向并不合理。

3 算例

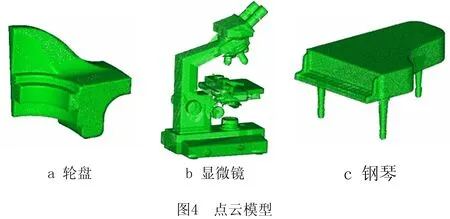
为验证本文法向估计结果的准确性，在硬件配置为Inter(R)Xeon(R)CPU 5120，1.86 GHz，2.0 GB内存，GNU/Linux操作系统环境下，采用Mura算法、Cao算法和本文算法对不同点云模型进行实验。如图4所示，轮盘、显微镜、钢琴模型均含有棱边和尖角等复杂特征。

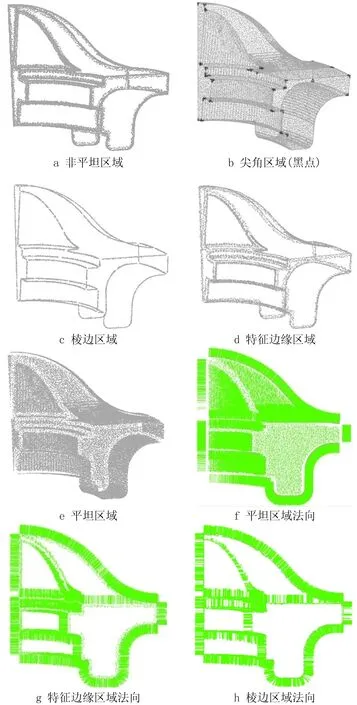
如图5所示，对轮盘模型的三维点云数据进行法向估计实验，由于点云分布较均匀，实验中设置k=10，从点云中随机抽取1 000个采样点并搜索每个采样点的k近邻，对于每一采样点，计算其与邻域中最远点的距离，然后将1 000个采样点的距离平方和求平均，用该平均值区分平坦与非平坦区域的阈值，即ε=0.03。计算样点的邻域到其局部拟合平面的残差平方和，并将大于ε的样点归为非平坦区域，非平坦区域的识别结果如图5a所示；对于非平坦区域中的任一样点，剔除其邻域中的非平坦区域点，并将剩余点进行聚类分析，基于分类数量将其划分为尖角、棱边、特征边缘区域，分别如图5b～图5d所示，图5e是去除尖角、棱边、特征边缘等特征的平坦区域。在计算法向过程中，首先采用主元分析算法计算平坦区域样点的法向，然后以平坦区域样点为初始法向，逐级向特征边缘、棱边、尖角区域样点传播，各区域的法向估计结果如图5f～图5i所示，特征区域样点的法向估计结果与其邻近平坦区域样点的法向保持一致，图5j所示为轮盘模型全部样点的法向。

采用Mura算法、Cao算法和本文算法对图4c所示含有棱边、圆角且采样不均匀的钢琴模型进行法向估计，结果如图6所示。3种算法在圆角特征区域的法向无明显区别，但是在棱边区域，本文算法样点的法向估计结果准确，棱边上的样点存在多义性法向，且多义性法向的夹角近似为邻接面的夹角；Mura算法出现法向光滑过渡现象；Cao算法棱边区域法向虽未被完全平滑处理，但法向准确性明显低于本文算法。

为进一步展示本文算法在棱边和尖角区域样点法向计算的准确性，将图4b中含有大量棱边和尖角特征的显微镜模型作为实验对象进行实验。图7所示为不同算法在其中一特征区域的法向计算局部放大图，图中的特征区域由3个平面相交产生，Mura算法和Cao算法棱边区域样点的法向在一定程度上被平滑处理，本文算法则能准确识别特征区域样点所属的平面，其法向估计结果与邻近平坦区域样点的法向保持一致，从图中可见，邻接面上相近的两点法向夹角近乎为两平面夹角，而且尖角点存在3个方向的法向。

为测试法向估计的稳健性，需对法向估计结果进行定量分析，故基于法向偏差均方根(Root Mean Square，RMS)统计棱边和尖角区域样点法向估计误差，其中RMS的计算公式为

(3)

f(〈nref,nest〉)=

(4)

式中：nref和nest分别为单位标准法向和估计法向；|S|为曲面采样点的总数量；τ为角度阈值，根据文献[20]取τ=π/18。

图4a中轮盘模型的点数为53 720，将其分别添加0，15%，25%，35%的高斯噪声，其中高斯噪声的标准差为0.01，利用Mura算法、Cao算法和本文算法对该点云在不同噪声下进行样点法向计算，统计3种算法所得结果的RMS值和法向出错样点数量Nbad-point，结果如表1所示，可见Cao算法和Mura算法所得法向出错样点数量随噪声含量的增大而明显增大。对于噪声含量为25%的数据，3种算法所得结果及法向出错样点如图8所示，Cao算法和Mura算法估计结果中的法向出错样点数量较多，主要分布于棱边和尖角区域，而本文算法估计结果仅存在少量法向出错样点。

表1 3种算法在不同噪声下的法向出错样点数和RMS值

为进一步测试法向计算的准确性，以25%高斯噪声下计算的法向为例，通过堆积图统计3种算法计算结果中法向出错样点的法向与其标准法向的角度偏差，结果如图9所示。可见，3种算法的法向出错样点主要集中在10°～18°角度偏差范围内，所占比例均超过50%，Mura算法、Cao算法和本文算法的比例分别为76.04%，81.76%，83.56%，本文算法角度偏差超过34°的法向出错样点的数量可以忽略不计。

4 结束语

本文提出一种针对含有棱边和尖角等特征的曲面采样点云法向估计方法，基于平坦区域样点法向的估计结果，逐级确定特征边缘、棱边区域和尖角区域样点的法向，该方法具有以下特点：

(1)基于样点对应曲面局部样本平面拟合结果的残差值，从点云中任一样点对应的曲面局部样本中剔除非平坦区域样点，从而使剩余的曲面局部样本数据具有可聚类性，可将曲面局部样本所属特征区域的识别问题转化为更加简单的k均值聚类分析问题。

(2)采用贝叶斯信息准则对特征区域的聚类优性进行量化，基于最优聚类划分结果的分类数量可准确推断样点所属特征区域的类型。

(3)基于平坦区域样点的法向估计结果，逐级确定特征边缘、棱边区域和尖角区域样点的法向，可提高特征区域样点法向估计结果的正确性，能保证棱边区域和尖角区域样点法向具有多义性，且对数据噪声具有抑制作用。

对于复杂型面采样点云，特征区域样点法向的多义性通常会破坏以曲面光滑为前提的法向一致性传播过程，导致各块平坦区域样点法向难以获得统一，拟对该问题进行进一步研究。