磁式滑移隔震体系及其在基础隔震中的应用

彭勇波,李 杰

(同济大学 土木工程防灾国家重点实验室,上海 200092)

作为一类研究和应用成熟的结构减震控制技术,隔震技术被广泛应用于工程实践,在提升结构安全性、改善结构功能性以及降低工程投资等方面发挥了重要作用[1-2]。从早期对建筑结构安全性的重视过渡到目前对建筑内部重要设施或精密仪器抗震性能的关注,现代隔震技术特别是具有自适应耗能能力的隔震体系大有用武之地。经过40余年的发展,以叠层橡胶隔震[3]、摩擦摆隔震[4]等为代表的隔震体系逐渐形成。然而,叠层橡胶隔震体系会放大地震波中的长周期成分,在近场强震作用下往往会出现较大的隔震层变形,易与周围挡墙发生碰撞,同时,其自身材料的长期稳定性能也存在问题;摩擦摆隔震体系在大震时可能产生过大的位移,且长期静止难以保证支座的摩擦系数,在设计中如何合理地选择或优化摩擦系数和复位刚度,保持摩擦系数长期不变等是提高隔震效果和性能的关键。在单一模式隔震体系基础上发展起来的组合隔震体系[5]构造繁琐,且经济性较差,而依赖于反馈控制算法的混合隔震体系[6]逻辑复杂,鲜有在工程中实施。

针对传统单一模式隔震体系存在的耗能能力弱、限位性能差等问题,作者近年来研究了一类基于电涡流耗能机制的磁式滑移隔震体系,并考虑不同的界面摩擦特性,研制了内磁式[7]和液磁式[8]滑移支座。通过开展隔震支座磁电耦合有限元模拟、理论推导和拟静力试验,建立了磁式滑移支座力-位移关系,揭示了内磁式滑移隔震支座(IMB)、液磁式滑移隔震支座(HMB)较铅芯橡胶支座(LRB)、摩擦摆支座(CSS)更优越的隔震性能。同时,开展了磁式滑移隔震结构振动台试验[9-10],验证了隔震系统的减震效能。

本文阐述了磁式滑移隔震体系的电涡流自适应耗能机制和可变限位模式,深入研究了磁式滑移支座力-位移关系,分析了磁式滑移隔震结构系统的场地适应性,开展了基于整体抗震可靠度的磁式滑移隔震结构系统优化设计,研究成果可为高烈度地震区传统隔震体系面临的瓶颈问题提供良好的解决方案。

1 磁式滑移隔震体系工作原理

磁式滑移隔震系统具有电涡流阻尼耗能和磁体互斥限位功能,由上层滑块和下层底座组成,接触面为铝板,滑块侧壁黏附或内置永磁铁,当上、下层发生相对运动时,切割磁感应线在铝板内产生电涡流,电涡流次生磁场形成阻尼力,抑制相对运动;同时,上、下层联结的永磁铁之间的排斥力限制滑块滑出边界。此外,界面摩擦力减阻上、下层相对运动。磁式滑移隔震支座原理如图1所示。

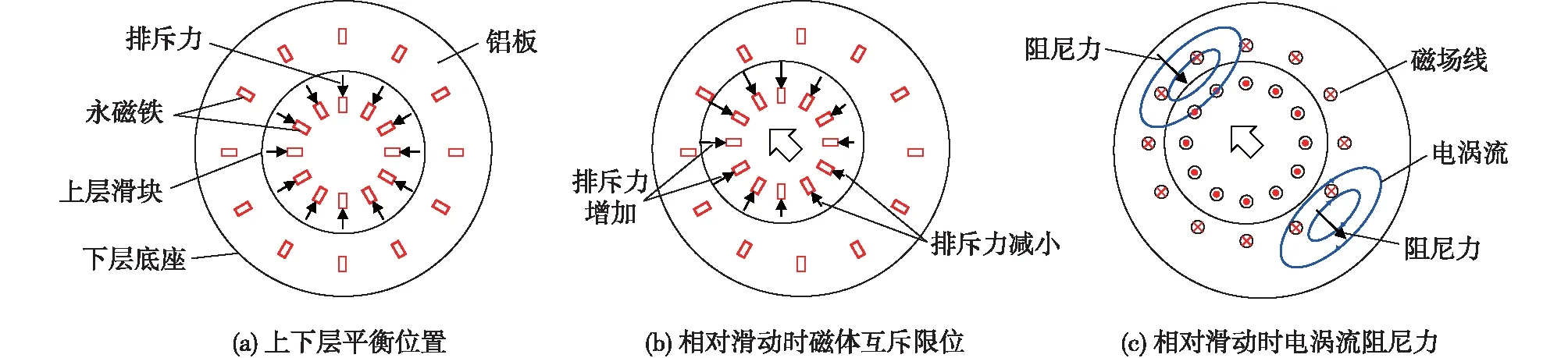
图1 磁式滑移隔震支座原理图

由图1可知:磁式滑移隔震支座的恢复力由摩擦力、排斥力和阻尼力三部分构成。摩擦力(Ffric)主要由铝板在滑移过程中产生,计算公式见式(1)。

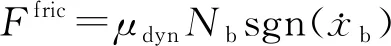
(1)

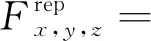
(-1)i+j+k+l+m+nφx,y,z(uij,vkl,wmn,r)

(2)

其中

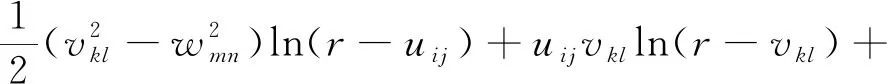
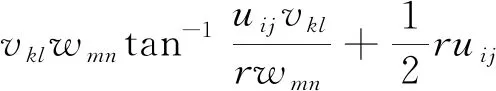
(3)

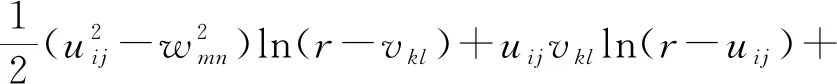
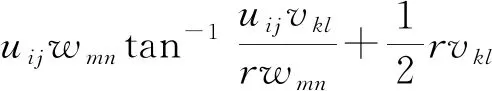
(4)

φz=-uijwmnln(r-uij)-vklwmnln(r-vkl)+

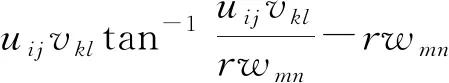
(5)

uij=α+(-1)ja′-(-1)ia

(6)

vkl=β+(-1)lb′-(-1)kb

(7)

wmn=γ+(-1)mc′-(-1)nc

(8)

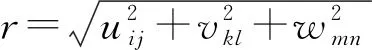
(9)

式中:Br和Br′为相互作用的两立方体永磁铁的剩磁强度;μ0=4π×10-7,为真空磁导率;两立方体永磁铁的尺寸分别为2a×2b×2c和2a′×2b′×2c′,中心沿着X、Y和Z轴距离分别为α、β和γ,磁化方向为2a×2b和2a′×2b′法向量方向,如图2所示。

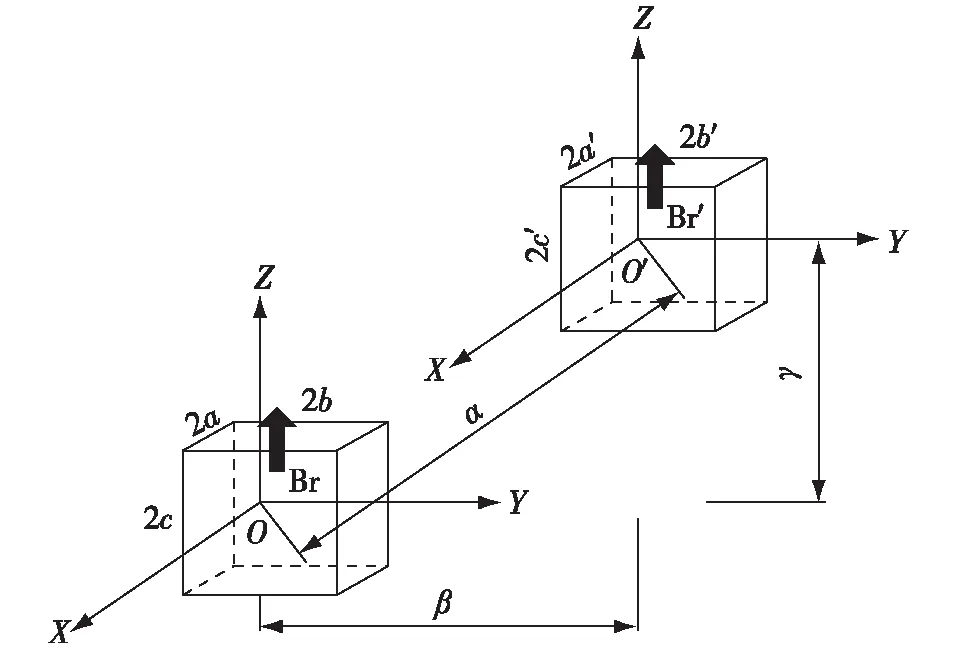
图2 立方体永磁铁位置和尺寸关系示意图

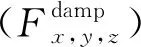
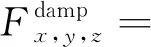
(10)

式中:Vx、Vy为滑移面滑块沿2个水平坐标方向的速度;Bx、By、Bz为空间坐标方向的磁场强度,采用有限元软件QuickField对空间磁场分布进行模拟得到;σ为铝板的电导率;δ为铝板厚度;rp为铝板半径;θ为极角;i、j、k为空间坐标方向的单位矢量。

假定支座沿着Y轴方向运动,即Vx=0,则

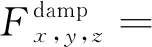
VyByBzk)ydθdy

(11)

由于磁场的对称性,Bx=0,则

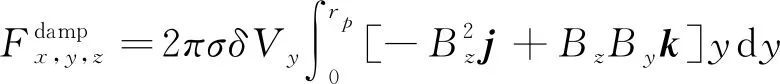
(12)

因此水平向的阻尼力可写为

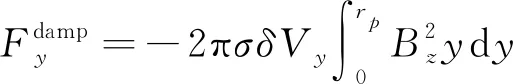
(13)

竖向的阻尼力可写为

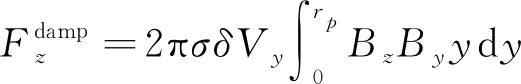
(14)

2 磁式滑移支座力-位移关系

2.1 内磁式和液磁式滑移支座

考虑不同的界面摩擦特性,研发了2套滑移隔震支座:以聚四氟乙烯板(PTFE)-铝板为滑动界面的IMB[7]和以高压机油-铝板为滑动界面的HMB[8],并以某两跨六层钢框架隔震结构振动台试验的缩尺模型为分析对象[9],进行IMB和HMB的设计,采用ABAQUS有限元软件进行了强度校核分析。图3—图6为IMB和HMB的设计图与研制样品。

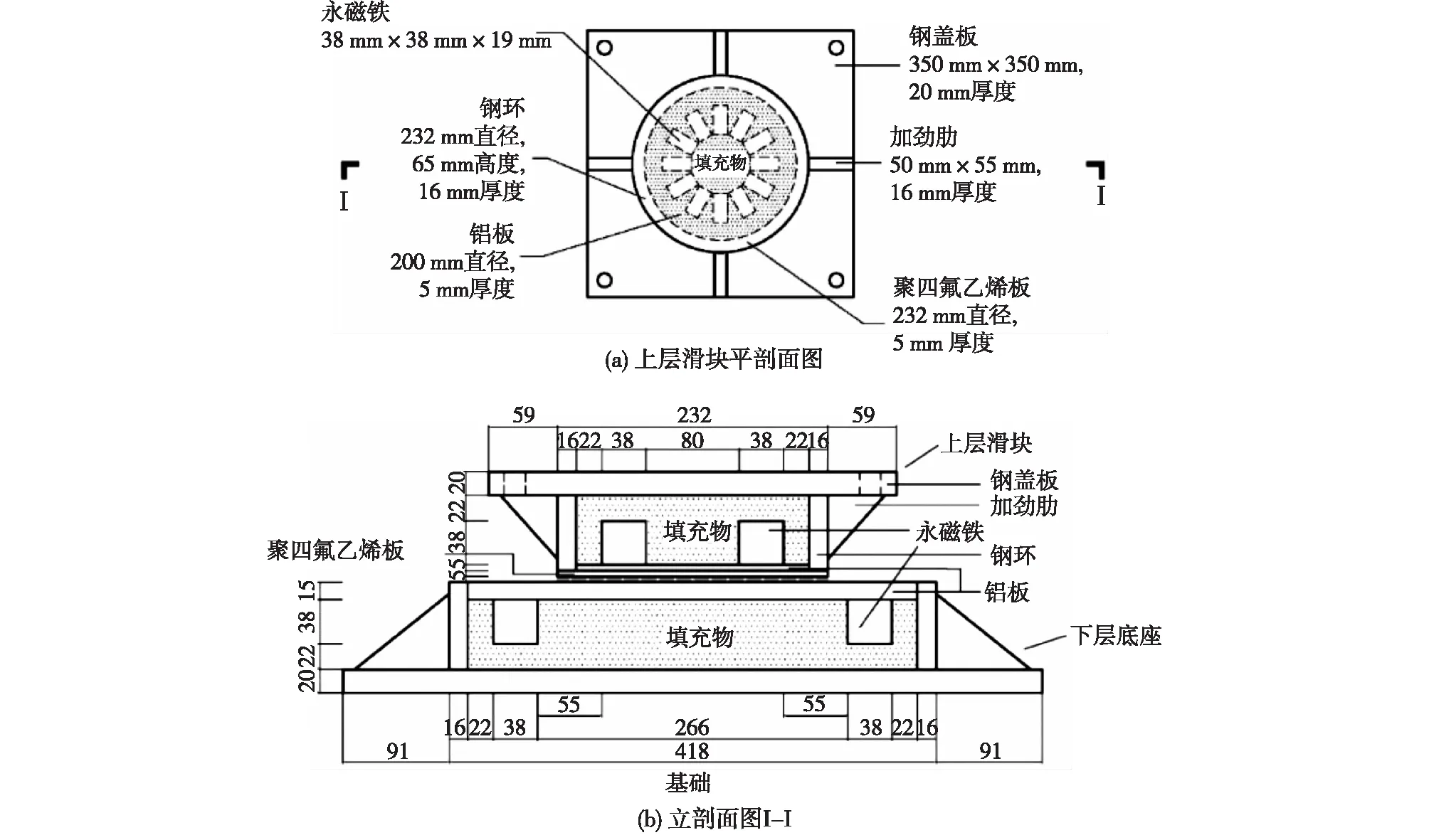
图3 IMB设计图

图4 IMB研制样品

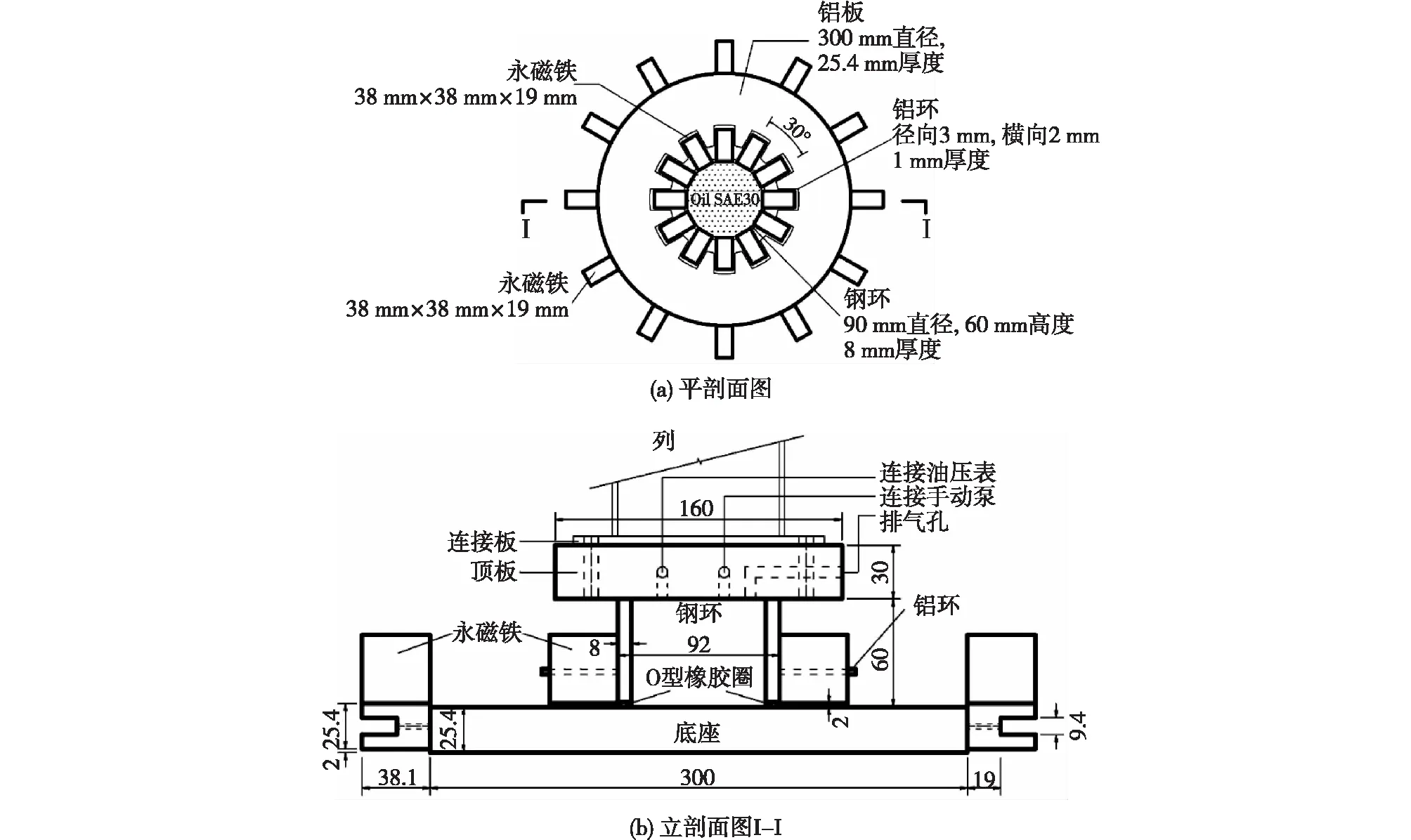
图5 HMB设计图

图6 HMB研制样品

IMB由上层滑块和下层底座构成,上、下层均由钢制盖板、钢环、内部填充(聚氨酯)、永磁体和两块层间垫板(抛光铝板和聚四氟乙烯板板)组成。相同尺寸的12块烧结钕铁硼永磁体(目前市面上磁性最强的磁铁),N极向外、S极向内均匀嵌置在上、下层滑块的聚氨酯填充物中。上、下层垫板均为T6061圆形铝板,上层滑块表面粘贴圆形聚四氟乙烯板。

HMB底板为T6061圆形铝板,滑移支座为钢环壁且底部带凹槽,顶板材料为Q345高强钢,钢环内密封高压机油SAE30。在支座外壁和底板外围分别贴附12块烧结钕铁硼永磁体,内、外圈磁铁一一对应,尺寸相同,沿径向同极相向。支座与底部铝板接触部位采用X型的O形橡胶圈(四分叶形),O形橡胶圈为派克精密标准件,选用邵氏硬度A70的丁腈橡胶(NBR)弹性体,安装在支座环壁底部凹槽内。

2.2 考虑高速滑移效应的磁式滑移支座力-位移关系

拟静力试验是揭示构件或装置系统恢复力特征的重要手段和方式之一。利用研制的磁式滑移支座,开展了滑移隔震支座拟静力试验。采用无锡市圣丰隔震器有限公司的三向液压伺服动静力加载试验机(竖向最大荷载50 t,水平X向最大动力荷载200 t,水平Y向最大动力荷载5 t,水平向最大位移均为 200 mm),进行Y向水平和竖向两向加载条件下IMB和HMB的拟静力试验:正弦位移波加载,竖向荷载分别为2、3和4 t,加载频率分别为0.05、0.10和0.20 Hz,位移幅值分别为20、35和50 mm。图7为IMB和HMB的恢复力-位移拟静力试验曲线(工况:竖向加载3 t,加载正弦位移波频率0.20 Hz,幅值20、35、50 mm)。从图7中可见:两者均具有与加载频率和加载幅值相关联的自适应特征,前者有显著的耗能特征,适用于速度脉冲丰富的近场地震动作用;后者有显著的限位特征、适用于长周期成分丰富的远场地震动作用。

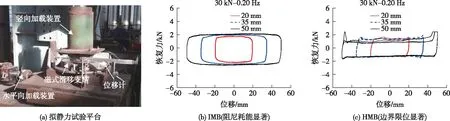
图7 磁式滑移隔震支座恢复力-位移拟静力试验曲线

结合理论分析、数值模拟[7]和拟静力试验可以看出,恢复力主要由三部分组成:与速度相关的阻尼力和滑动摩擦力,与位移相关的排斥力。阻尼力和排斥力幅值变化相差四分之一个周期;阻尼力与黏滞阻尼器的滞回特征相似,也与Duffing振子行为相似;排斥力随位移快速增大,与双曲正弦函数相似。因此,从阻尼力的表征角度,磁式滑移隔震支座的恢复力可以采用多项式模型(Duffing振子),排斥力采用双曲正弦函数表征,摩擦力采用符号函数。

对于IMB,恢复力(F)表达式为多项式模型,即

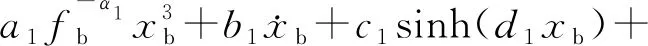
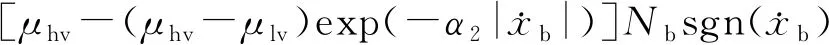
(15)

式中:xb为隔震支座的滑动位移;fb为滑动位移频率;α1为频率指数;a1、b1、c1、d1为待定参数;sinh(·)为双曲正弦函数;μhv、μlv分别为高速和低速下的摩擦系数;α2为摩擦指数,它的取值与摩擦面介质相关。

对于HMB,恢复力表达式亦为多项式模型,即

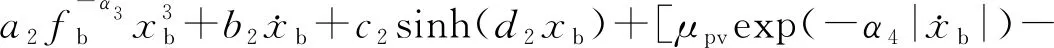
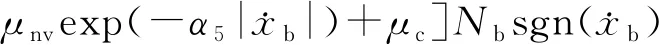
(16)

式中:α3为频率指数;a2、b2、c2、d2为待定参数;μpv和μnv分别为动摩擦系数峰值出现前后的摩擦系数;μc为摩擦系数校正项;α4、α5为摩擦指数。

摩擦系数和摩擦指数的精确识别对于磁式滑移支座隔震性能的标定非常关键。结合拟静力试验数据,分离出滑动摩擦力,识别得到动摩擦系数与滑移支座滑动速度的关系曲线,如图8所示。图8(a)为IMB的动摩擦系数与滑动速度的关系曲线,可以看到,指数型函数的拟合曲线与试验数据吻合,这与CSS的摩擦系数和速度的关系非常相似,即可以采用修正的库仑模型模拟IMB的摩擦系数。图8(b)为HMB的动摩擦系数与滑动速度的关系曲线,可以看到,尽管HMB的摩擦力也为库仑摩擦,但是由于其摩擦面为高压机油和铝板(液-固摩擦),其摩擦行为与IMB的聚四氟乙烯板和铝板摩擦面(固-固摩擦)不同。主要体现在:高速运动下,高压机油会出现剪变稀化的现象,导致动摩擦系数在速度较大时会出现明显的减小。

图9为参数标定后得到的IMB和HMB的恢复力-位移模型曲线。由图9可以看出,IMB的电涡流阻尼耗能效应显著:当滑移谐波位移频率为5 Hz时,最大速度处(位移为零)的恢复力增大22%(均为电涡流阻尼力的贡献),如图9(a)所示;然而,在较高的滑移谐波位移频率时,由于高压机油的剪变稀化,滑移面摩擦系数降低,HMB恢复力中电涡流阻尼力的增强小于库仑摩擦力减弱,总体表现为恢复力下降,如图9(b)所示。

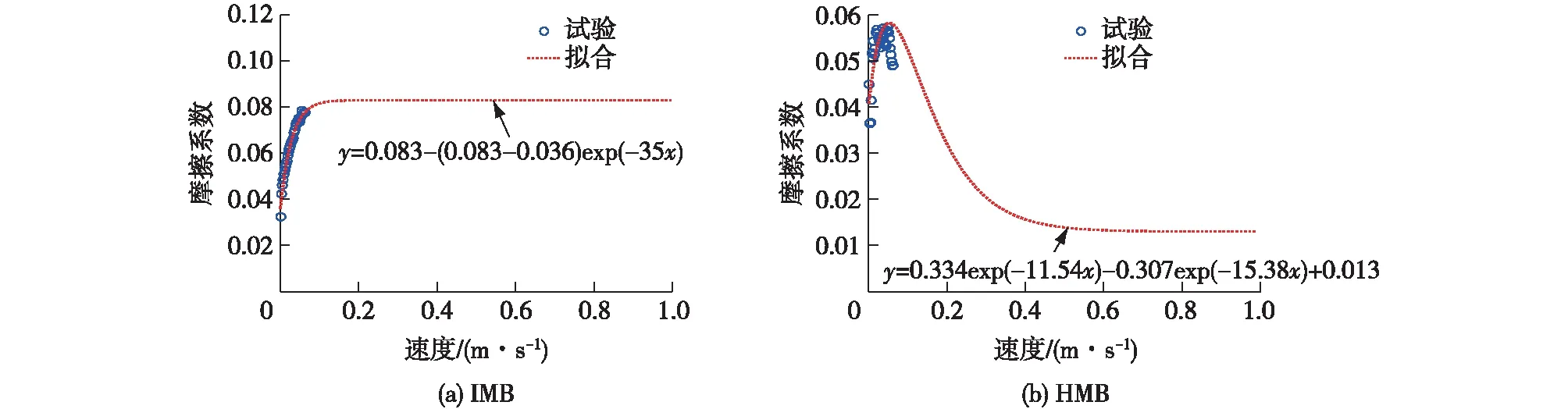
图8 磁式滑移支座摩擦系数与支座滑动速度关系曲线

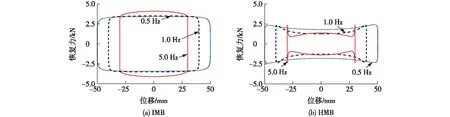
图9 磁式滑移支座恢复力-位移模型曲线

3 磁式滑移隔震结构系统的场地适应性

通过参数识别得到IMB和HMB恢复力模型中的参数。进一步研究分别附加IMB、HMB、CSS和LRB的两跨六层钢框架结构隔震结构系统的场地适应性,包括远场地震动(FF)、近断层无脉冲地震动(NF-NP)和近断层有脉冲地震动(NF-P)作用。其中,CSS和LRB的组成尺寸设计、模型参数定义依据《建筑抗震设计规范》(GB 50011—2010)、《叠层橡胶支座隔震技术规程》(CECS 126—2001)和标准《橡胶支座 第3部分:建筑隔震橡胶支座》(GB 20688.3—2006),采用双线性模型进行分析。

采用基于小波的速度脉冲识别方法[15],从美国FEMA-P695报告中选取了34个远场地震动分量、20个近断层无脉冲地震动分量和25个近断层有脉冲地震动分量,进而分析了峰值加速度0.2g远近场地震动作用下IMB、HMB、CSS和LRB的等效单自由度隔震系统的地震动响应。将各场地地震动和各类支座的平均减震率绘制在一张图上,如图10所示,纵坐标表示平均减震率,横坐标表示地震动类型和场地类别。此外,不同场地条件地震动(包括远场地震动、近断层无脉冲地震动、近断层有脉冲地震动)作用下各类隔震体系的峰值水平位移绘制于图11。

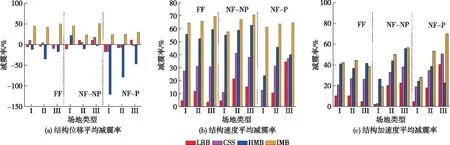
图10 不同场地条件下各类隔震体系的平均减震率

由图10可以看出:隔震体系IMB在各类地震动作用下位移平均减震率变化并不是十分明显,仅在NF-P作用下位移减震效果有所降低,但较其他3种支座仍具有较小的位移,始终处于位移限值内。隔震体系LRB、CSS和HMB在FF和NF-NP作用下,隔震位移几乎与无隔震位移一致,少数情况有放大现象、且存在超越阈值的可能。由图11可以看出:在NF-P作用下隔震位移明显增大,隔震体系HMB尤为明显,尽管随着场地土变软,隔震位移逐步减小,但是在NF-P作用下HMB位移峰值有较大概率超出限值。

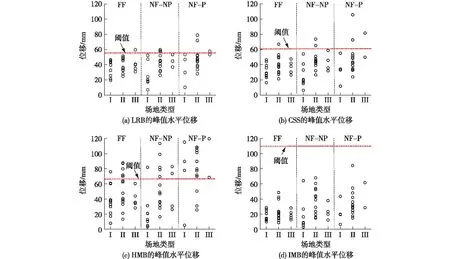
图11 不同场地条件下各类隔震体系的峰值水平位移

IMB对于速度的控制效果非常明显,在各类场地、远近场地震动作用下,均保持60%左右的减震率。HMB在FF和NF-NP作用下效果与IMB相当,但是在应对NF-P时,速度减震效果明显下降。CSS对于速度的控制效果明显比IMB和HMB差,但是优于LRB。

对于FF,各种隔震支座在不同场地地震动作用下加速度减震效果几乎一致,其中,IMB和HMB最好,CSS次之,LRB最差。而对于近断层地震动,无论有、无脉冲,随着场地土变软,各种隔震结构的隔震效果总体上逐步提升。在NF-NP作用下,IMB和HMB减震效果最优,CSS次之,LRB最差;但是在NF-P作用下,HMB的减震效果显著下降、在III类场地条件最差,IMB始终保持最好的减震效果。

综上所述,隔震体系IMB在各类场地、远近场地震动作用下,无论对结构位移,还是对结构速度、结构加速度的控制均有出色表现,在考察的4种隔震体系中减震效果最优,因此具有卓越的工程适用性。隔震体系HMB在FF和NF-NP作用下,控制效果显著,与IMB相当,但是由于其液-固摩擦的剪切稀化效应,导致在NF-P作用下控制效果急剧下降,因此HMB适用于FF和NF-NP,不推荐用于NF-P。隔震体系CSS与IMB相似,在各类场地、远近场地震动作用下,表现差异性并不明显,控制效果均弱于IMB,但好于LRB,因此CSS也具有良好的工程适用性。LRB在各类场地、远近场地震动作用下的减震效果总体上较前3种隔震体系差,因此从技术层面不推荐采用。此外,HMB和LRB的位移控制较差,在基础隔震设计中需要附加装置(如黏滞阻尼器)或通过半主动、智能控制(如HMB油压实时调节,LRB与磁流变阻尼器、形状记忆合金等联合使用)限制隔震层位移。

4 基于可靠度的磁式滑移隔震结构优化设计

以内磁式滑移隔震结构振动台试验模型[9]为分析对象,采用SAP2000有限元分析软件对试验模型进行建模分析,进而利用静力凝聚方法得到6种自由度集中质量模型,在此基础上,采用概率密度演化理论[16],以工程随机地震动模型为输入[17],进行了磁式滑移隔震装置施加前后结构随机地震响应分析与可靠度评价。图12为罕遇地震作用下(地震动峰值加速度0.51g)结构层间位移等价极值的概率密度及概率分布。由图12可以看出：施加IMB后,结构层间位移响应的均值向左、偏小方向移动,变异性降低;同时,结构安全的可靠度由施加磁式滑移隔震装置前的0.831提升到1.000,表明IMB能有效增强结构抗大震的能力。

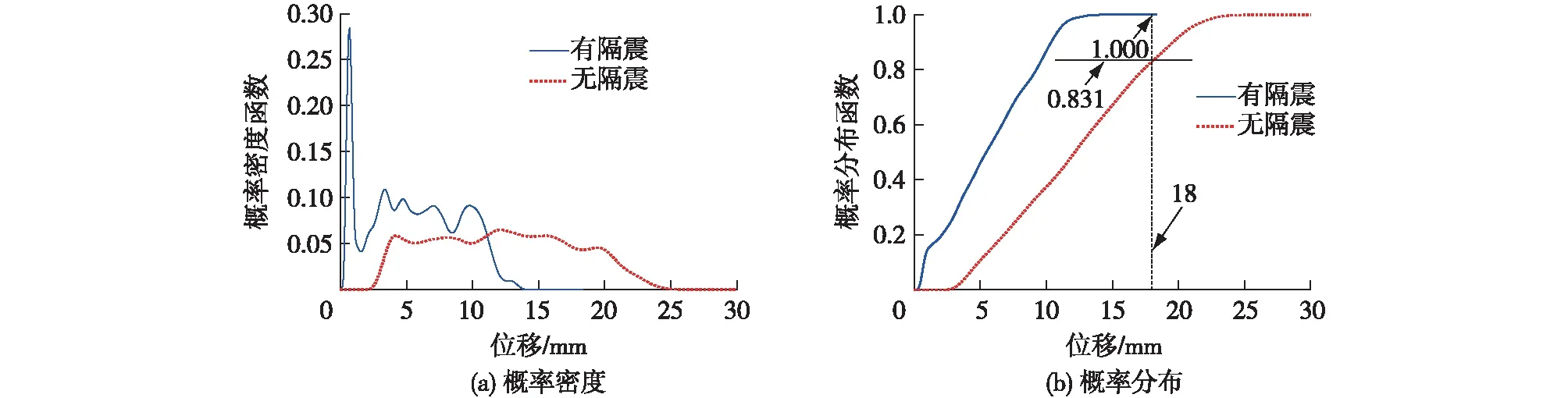
图12 罕遇地震作用下结构层间位移等价极值的概率密度及概率分布

隔震层变形是隔震结构系统失效模式研究的重要方面。为了揭示罕遇地震作用下内磁式滑移隔震系统的可靠性,对隔震层变形做了概率密度演化分析和可靠度评价。图13为多遇(0.11g)、设计(0.20g)、罕遇(0.51g)地震作用下隔震层位移等价极值的概率密度及概率分布,由图13可以看出：在多遇和设计地震作用下,隔震层具有足够的可靠性;然而在遭受罕遇地震时,隔震层的可靠度为0.842,表明需要针对隔震层开展基于可靠度的优化设计研究。

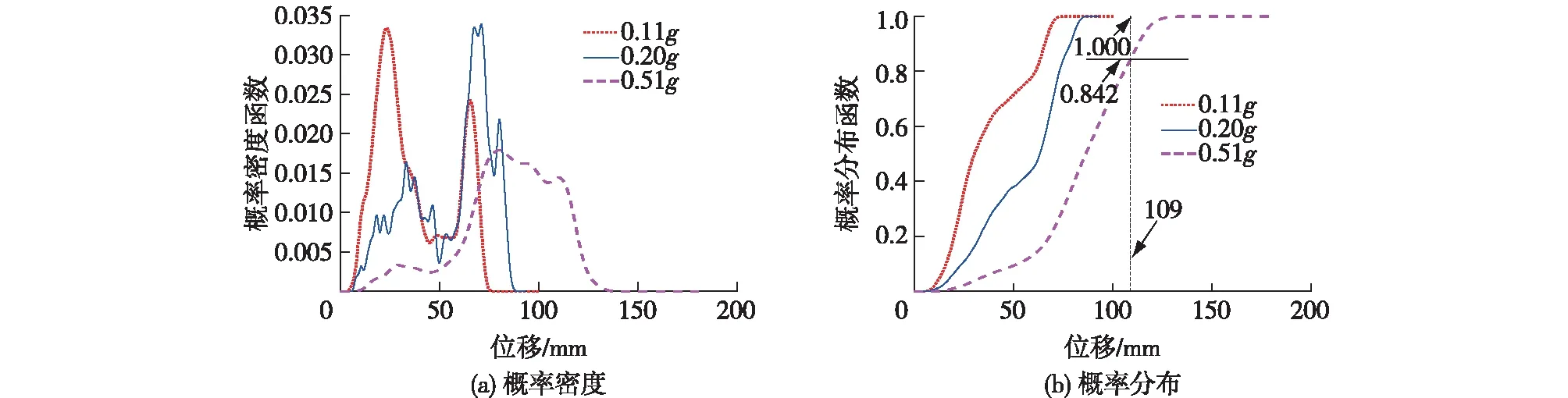
图13 多遇、设计、罕遇地震作用下隔震层位移等价极值的概率密度及概率分布

首先采用方差敏感性分析方法,分析了正弦位移加载和天然地震动作用下隔震层模型参数的全局敏感性。在本文中,IMB的模型参数有8个,包括频率指数α1,待定参数a1、b1、c1、d1,高速和低速下的摩擦系数μhv、μlv,摩擦指数α2。分析表明,与摩擦力相关的摩擦系数和摩擦指数为最敏感的3个参数。

根据国际结构安全性联合委员会(JCSS)发布的规范规定[18],结构构件在中等造价时的失效概率为0.05,因此对于隔震支座的可靠度应大于0.95。在前述分析中,遭受罕遇地震时隔震层的可靠度为0.842,不满足规范要求,由此应构建以磁式滑移隔震支座变形可靠性为约束、以隔震结构层间位移整体可靠度最大为目标的优化准则,进行磁式滑移隔震体系模型参数优化设计。基于可靠度的磁式滑移隔震结构优化设计准则见式(17)。

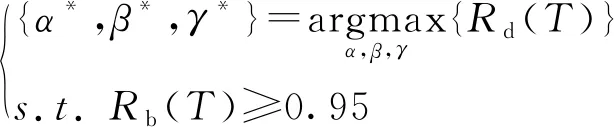
(17)

式中:Rb、Rd分别为隔震层可靠度和隔震结构层间位移整体可靠度;α、β、γ表示与摩擦力相关的摩擦系数和摩擦指数。

采用遗传算法进行上述参数优化,得到摩擦系数μhv、μlv,摩擦指数α2分别为0.164、0.05和69.8。进一步分析表明,优化后在罕遇地震作用下隔震层位移可靠度可达0.966,较优化前提升了15%,如图14所示。因此,基于可靠度的隔震体系优化能显著提升隔震结构的抗震性能。同时,比较优化前后隔震层IMB在正弦波位移下的恢复力曲线,如图15所示,可以看到,优化后隔震层抵抗滑移变形的能力和耗能能力均提升了一倍。

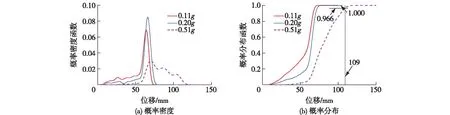
图14 优化后多遇、设计、罕遇地震作用下隔震层位移等价极值的概率密度及概率分布

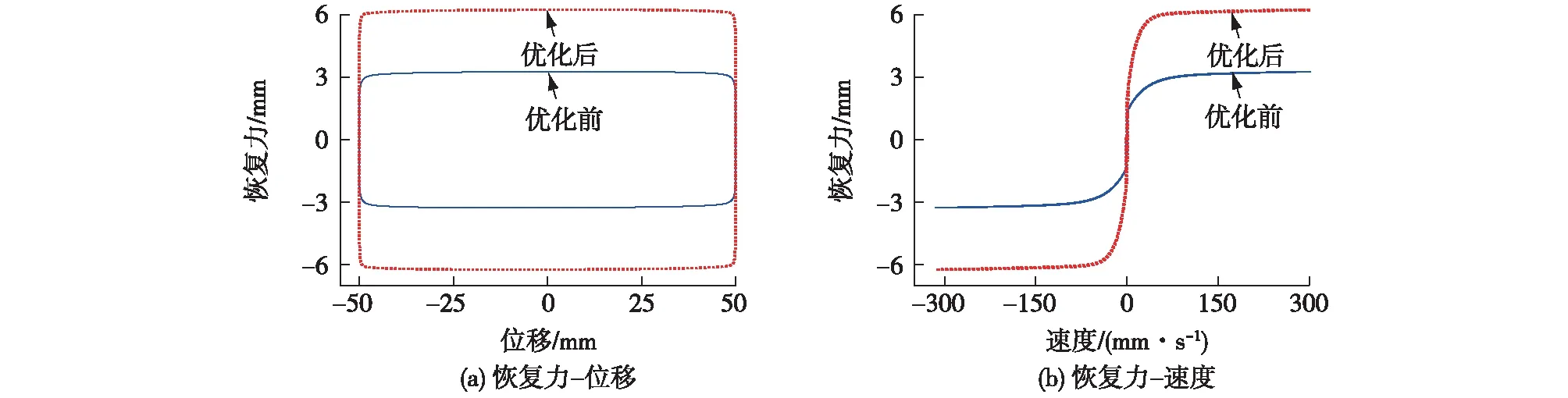
图15 优化前后IMB在正弦波位移下的恢复力曲线

5 结论

1)研究了基于电涡流自适应耗能机制和可变限位模式的磁式滑移隔震体系,考虑不同的界面摩擦特性,研制了IMB和HMB。

2)通过开展隔震支座磁电耦合有限元模拟、理论推导和拟静力试验,揭示了磁式滑移隔震体系的工作原理,建立了考虑高速滑移效应的磁式滑移支座力-位移关系。

3)分析了磁式滑移隔震结构系统的场地适应性,揭示了IMB、HMB较LRB、CSS优越的隔震性能。

4)开展了基于可靠度的磁式滑移隔震结构优化设计,建立了隔震结构系统性能提升的概率优化方法。

致谢

刘伟庆教授生前致力于结构抗震、减震研究,在诸多方面做出了重要贡献。本文作者曾有幸与他合作、开展了高烈度地区隔震结构的随机地震反应分析与抗震可靠度研究,获益良多。谨以此文纪念刘伟庆教授。