传统木结构建筑斗栱力学性能研究进展

2021-05-31刘杏杏陆伟东程小武吴伟强

南京工业大学学报(自然科学版) 2021年3期

刘杏杏,陆伟东,程小武,吴伟强

(1.南京工业大学土木工程学院,江苏南京 211800;2.南京工大建设工程技术有限公司,江苏南京 211800)

我国木结构建筑历史悠久,自河姆渡时期,人们就开始运用榫卯的连接形式,发展至明清时期,木结构的建筑形态和建造技艺已趋于巅峰。这其中最具代表的当属殿堂型木结构建筑,殿堂型木结构是等级最高、结构最复杂的古建筑结构形式,在我国建筑史中具有独特的地位,其大屋顶、深出檐的特征充分体现了建筑的恢宏气势,因此被大量应用于高等级的寺庙、宫殿建筑中(图1和2)。我国目前留存的殿堂型木结构建筑数量众多,它们屡经灾害而不倒,成为我国乃至世界的建筑文化遗产,其独特的结构性能和抗震机制值得不断地深入研究。

图1 五台山佛光寺东大殿

图2 太原晋祠圣母殿

斗栱是殿堂型木结构建筑的显著特征之一,也是中国传统建筑文化的标志性元素。斗栱在不同时期有不同名称,又被称作铺作、斗科、枓栱、欂栌等(本文中统一称为斗栱),是由水平放置的方形斗、升、栱和斜置的昂组成,如图3所示[1]。斗栱在结构上具有传递荷载、减小跨度、增加出檐等作用,在殿堂型木结构建筑中,通过柱头、补间、转角铺作的巧妙结合形成了铺作层,铺作层的竖向层叠变形和水平摩擦变形契合了现代结构的减震理念[2-3],充分体现了我国古人的建筑智慧。

1 斗栱的演变及分类

1.1 西周至南北朝时期

在早期,以土木为建筑材料的建筑体系中,为了保护夯土台基以及土墙免受雨水淋洗,建筑的出檐尤为重要。为了保证出檐要求,最简单的承檐结构就是擎檐柱,考古发掘表明,在商代已经使用了擎檐柱。此后,发展出了斜撑、插栱,到战国时期,插栱与横栱结合在一起,形成了斗栱的雏形。汉代以后开始在柱间使用斗栱,最初是一种在现代被称为人字栱的斗栱,即在额枋上立一个叉手,上置一斗,用于承托檐檩,如图4所示。南北朝时期,斗栱的栱端已经有明确的卷杀,此时已经将美观融入到斗栱之中,如补间用的人字栱由直线变为曲线[4]。

1.2 唐至元时期

唐至元时期是斗栱发展的高峰期,斗栱的结构机能和造型艺术在这阶段完美地结合在一起[5]。唐代斗栱的构造已经完全成形,形式丰富、各类构件完善,之后历代的斗栱构件都是在此基础上不断变化,唐代斗栱雄大壮阔,其高度可以达到柱高的一半,佛光寺东大殿柱头铺作即为唐代典型斗栱结构(图5(a))。到了宋代,我国古代建筑已经发展到了较高水平,李诫编制的《营造法式》是我国古代最完整的建筑技术书籍[6],提出的材份制概念使得斗栱的分类与做法趋于规范化。唐宋时期的斗栱最显著的特点是下昂的使用,昂在结构中具有杠杆的作用,用于平衡昂头和昂尾的屋面荷载。到元朝时期,昂逐渐由斜向转变为水平向,其结构作用也发生变化,如河北正定县阳和楼的单抄双下昂(图5(b))。此外,唐至元时期内的斗栱通过柱头、补间和转角的结合形成了铺作层,铺作层介于柱架层和梁架层之间,具有耗能减震作用。

1.3 明清时期

明朝时期斗栱是处于元和清的过渡期,柱头铺作、转角铺作与明之前的变化不大,而在局部构造上发生了变化,如将斜向的昂转变成了平昂(图5(c))。清雍正十二年《工程做法则例》问世,对斗栱的名称、构造、外观、尺寸进行了新的规定[7]。此时的斗栱与之前的斗栱形式有了较大的变化,其作为结构的作用减退,更偏向于装饰作用。由于房屋出檐距离的收缩,斗栱的尺寸也显著缩小,斗栱高度仅为柱高的1/10～1/8。明代斗栱还多用真昂,清式斗栱则逐步削减了昂的作用,斗栱里侧采用斜向拽架、外侧为水平昂嘴,谓之溜金斗栱[8]。清式斗栱另一个较大的变化在于乳栿变成了桃尖梁(图5(d)),桃尖梁置于柱头之上,而非像乳栿一样插入栱中,柱头科支撑挑檐的作用被梁取代。随着建筑功能需求的变化、建造技艺的发展和建筑审美的变化,明清时期的斗栱逐渐形成了其独特的风格特征。

图5 各时期斗栱演变过程[7]

1.4 斗栱分类总结

从斗栱的发展和演变过程可以看出,各个时期的斗栱具有不同的形式特征和功能作用。唐代以前的斗栱仅在墓葬中发现了少量遗迹,且该时期的斗栱结构简单,科学研究价值较弱;唐至元时期的斗栱在建筑中开始发挥重要的结构作用,其抗震机制应进行深入探究,另外该时期的木结构建筑仍有少数保留至今,且已成为国家重点文化保护建筑,亟需进行科学合理的保护和修缮。明清时期的斗栱是在唐宋斗栱形式之上,根据建筑功能、建筑审美、建造材料的变化演变而成的,是自成体系且同样发展至技艺巅峰的斗栱形式。现有关于斗栱性能的研究主要集中于唐宋时期和明清时期的斗栱,本文从斗栱的竖向承载、水平抗震、铺作层抗震作用以及斗栱有限元分析4个方面对国内外的研究进行了梳理归纳,对斗栱的研究现状进行总结并提出可能的后续研究方向。

2 斗栱竖向承载力学性能

2.1 试验研究及破坏形态

斗栱通过挑檐桁、正心桁以及栱与栱之间的挤压层层传递屋面荷载至下部结构。通过这种方式,斗栱可以支撑屋面的出挑,传递竖向荷载至柱架层。斗栱竖向加载试验是研究斗栱竖向承载力和破坏模式的直接方法,现有研究中竖向加载试验主要采用两种加载方法:一种是正向加载,荷载施加于乳栿上;一种是倒置加载,以慢栱为支座,栌斗为施加荷载端。

谢启芳等[9]对叉柱造式斗栱节点进行了竖向加载试验,荷载施加于柱端,试验中栌斗最先开始出现裂缝,并最终发展至栌斗木材劈裂、斗耳木材压屈破坏。肖碧勇[10]对应县木塔双抄双下昂七铺作斗栱进行了竖向加载试验,试验模拟了屋面实际荷载施加模式,采用分载梁施加于橑檐枋和草乳栿,如图6(a)所示。陈志勇[11]对应县木塔第二层平坐层两种外槽柱头斗栱铺作进行了竖向加载试验，试验破坏形态均为底部栌斗和泥道栱先破坏，继而发生华栱破坏，直至斗栱丧失承载力。文献[12-13]对应县木塔中典型的3种柱头铺作、补间铺作、转角铺作进行了竖向荷载试验,试验采用斗栱倒置加载法(图6(b)),加载后试验破坏为栌斗破坏。文献[14-16]对会善寺大雄宝殿斗栱进行了竖向加载试验,发现栌斗与头昂、泥道栱交汇处易发生剪切、承载破坏,斗栱的分层变形峰值均为头昂最大、二昂次之、蚂虾头最小,试件竖向的延性系数较好。

斗栱在竖向荷载作用下的传力机制是从上至下逐层传递至栌斗,越靠近斗栱下部的组件承受的荷载越大。因此,试验研究中的破坏形态主要表现为斗栱下部的华栱折断、栌斗劈裂等,而斗栱上部的昂、慢栱、瓜子栱等组件由于只承受部分荷载的作用,未发生明显的破坏现象。

2.2 力学模型

中国传统建筑对于斗栱的选用,通常是依照房屋建筑等级、用材规格来确定形式和尺寸的,对斗栱竖向受力机制没有深入探究。斗栱在竖向荷载作用下,由于木材的局压变形,斗栱的刚度、承载力会发生变化,通过建立力学模型推导出斗栱的竖向承载力和竖向刚度理论公式是研究斗栱力学性能的关键。

魏国安[17]和高大峰等[18-19]通过对斗栱进行竖向承载力试验和有限元分析,提出了三折线的斗栱竖向变刚度力学模型,同时考虑了斗栱的竖向隔震作用,采用竖向弹簧和阻尼器建立斗栱的单自由度线性阻尼系统模型(图7)。吕璇[20]认为斗栱竖向刚度可采用三折线模型描述,在竖向偏心荷载下的转动刚度可采用两折线模型描述。程小武等[21]通过试验发现斗栱在栌斗层出现塑性破坏,而上部斗栱依然处于弹性状态,提出了以栌斗与华栱接触面为界,将斗栱竖向刚度简化为两个竖向弹簧的串联模型来进行描述。周乾等[22-23]对故宫太和殿一层和二层中3种不同的清式斗栱节点进行了试验研究,提出了三折线形式的竖向刚度模型。

图6 斗栱不同竖向加载方式

图7 斗栱竖向弹簧-阻尼器模型[17]

中国台湾地区、日本的研究者对斗栱的竖向承载力学性能也开展了众多研究,提出了不同的斗栱竖向承载力学模型。Yeo等[24]对不同的竖向与水平荷载组合下的足尺叠斗模型进行了拟静力试验,研究了叠斗节点弹性和屈服后的结构性能,并由模型的破坏模式建立了节点的力学模型。日本东京大学的学者们[25-27]选取大斗肘木、平三斗、出三斗、出组4种日本斗栱基础构造形式,通过斗栱的振动台试验及拟静力加载试验分析其恢复力特性、斗栱变形特征及刚度,建立了斗栱刚性的弹簧简化模型。

上述研究均指出斗栱在竖向受力时,具有三折线的变刚度力学特征,如图8所示,这与斗栱中组件的横纹受压性能有关。由图8可知:在加载初期,斗栱处于弹性受力阶段,由于木材横纹受压弹性模量低以及存在初始的安装间隙,此阶段的弹性刚度(k1)较低;随着荷载进一步施加,斗栱部分组件进入屈服状态,木材横纹受压屈服后性能进入强化阶段,斗栱整体刚度(k2)呈现出增大的趋势;当斗栱部分组件随着荷载施加出现破坏时,如华栱开口处木材劈裂、栌斗劈裂等现象,斗栱刚度(k3)开始下降直至最终破坏。三折线的力学模型较为清晰地诠释了斗栱竖向加载下的受力特征。

图8 竖向刚度三折线模型

3 斗栱水平抗震性能

3.1 试验研究及破坏形态

斗栱在水平荷载作用下,通过栱与栱之间的摩擦和挤压,使得斗栱具备一定的耗能作用,这种耗能作用与斗栱的形式、尺寸有关,研究者们对不同形式的斗栱开展了水平荷载试验研究。

图9 斗栱及其滞回曲线[31]

明清时期的斗栱尺度和构造与唐宋时期的斗栱相比有明显的差异。邵云等[32]对六朵八等材宋式斗栱及一攒三跳柱头科清式斗栱足尺模型进行了低周反复荷载试验,研究认为两者都具有较好的整体性和转动能力,但宋式斗栱具有更高的抗侧刚度和承载力。周乾等[33-34]对故宫太和殿一层、二层柱头科，平身科，角科的1∶2缩尺模型进行了反复荷载试验，加载时采用斗栱倒置,分别在坐斗的横向和纵向两个方向进行水平加载,试验中斗栱的各构件间不断发生摩擦和滑移,但未出现明显的构件破坏现象。

3.2 恢复力模型

斗栱恢复力模型是斗栱抗震性能的重要表征方式,是对斗栱滞回性能的总结归纳。国内学者对斗栱的水平恢复力模型开展了大量研究,总体可分两类:第1类为双线形恢复力模型,文献[35-38]基于双线形强化弹塑性模型,通过实验分析,提出恢复力模型的弹性刚度与竖向荷载呈正相关;第2类为三线形恢复力模型,文献[39-40]搜集了27个4种典型宋式斗栱的试验数据,在OpenSees有限元软件内置的Hysteretic材料恢复力模型基础上,提出了基于试验参数分析的斗栱简化滞回模型。文献[41-42]对4种斗栱节点进行了动力荷载和静力荷载试验,提出了斗栱节点的滞回模型以及模型侧向刚度的计算方法。

由上述研究可以得出,斗栱在水平荷载作用下具备一定的耗能能力,并且在多铺作组合下抗震性能比单铺作下更优越。现有研究提出了不同类型的斗栱恢复力模型,但主要基于试验数据的拟合,尚未形成统一的斗栱恢复力模型,制约了相应数值模型的深入分析和应用。

4 铺作层抗震性能

铺作层位于殿堂型木结构建筑的柱架层和梁架层之间,在地震作用下可以通过铺作的摩擦和变形耗能降低梁架层的地震响应,具有耗能减震的作用。基于此,国内众多学者开展了铺作层的抗震性能研究,采用现代建筑的结构减震、隔震理念去解析我国古建筑的抗震原理。

4.1 振动台试验

铺作层是由多种不同形式铺作共同组成,铺作数量、铺作间距、铺作间的联系是影响铺作层抗震性能的重要因素。潘毅等[43]研究了铺作层斗栱尺度、斗栱数量对木结构抗震性能的影响,结果表明:在强震作用下,斗栱布置数量越多、布置越对称,铺作层对地震动加速度的衰减作用越明显,斗栱铺作层的侧向变形也越小;而当斗栱的尺度减小后,虽然仍可降低斗栱铺作层的侧向变形,但对地震动加速度的衰减作用却不明显。王娟等[44]对唐代殿堂型木结构单间四柱空间木构件进行了抗侧力性能研究,探究了铺作层构造、柱脚和柱头节点形式、竖向荷载大小和位置对木构件抗侧力性能的影响。现有铺作层振动台试验研究大多仅建立了柱架层和铺作层模型,对于梁架层则采用刚性板或者附加质量进行模拟,较少考虑铺作层对含有梁架层的整体建筑抗震性能的影响。

4.2 铺作层减震、隔震理论模型

铺作层在地震作用下刚度、阻尼等动力响应的变化是影响铺作层耗能减震作用的关键因素。赵均海等[45]首次对中国古建筑中清式斗栱进行了动力试验研究,得到了斗栱模型的频响函数曲线以及边界条件、竖向荷载等对固有频率和阻尼比的影响。李海娜[46]推导了铺作层的水平刚度和阻尼比的计算公式,提出了铺作层隔震结构水平和竖向的动力分析模型。薛建阳等[47]通过对柱架层和铺作层的振动台试验,基于能量分配系数建立了柱架层和铺作层的地震破坏评估模型。张锡成[48]对单层单开间殿堂结构当心间模型进行了振动台试验,提出了综合考虑柱础滑移隔震、半刚性榫卯节点的特性及铺作层耗能减震特性的木结构简化计算模型。李飞[49]以西安箭楼中斗栱为研究对象,通过对清式单体和组合斗栱节点进行抗震性能试验,提出了将斗栱层的横向隔震等效为多个单自由度体系的并联模型。

铺作层的减震、隔震性能是研究殿堂型木结构建筑抗震性能的关键,铺作层抗震效应除了与铺作层自身的刚度和阻尼相关外,还与上、下部结构质量和频率的比值相关,目前的减震、隔震理论模型较少考虑木结构梁架层对铺作层动力反应的影响。

5 斗栱有限元分析

5.1 木材非线性本构关系模拟

木材是一种各向异性的材料,受拉和受剪时具有脆性破坏特征,顺纹受压时具有屈服破坏特征,横纹受压时会发生二次硬化,除此,木材在各个方向的材料力学性能也有极大差别,顺纹方向的强度和弹性模量大于横纹方向的[50-51]。因此,木材的本构模型非常复杂,如图10所示,XT、YT和ZT分别为木材顺纹纵向(L)、横纹径向(R)和横纹切向(T)的抗拉强度;XC、YC和ZC分别为木材L、R和T三向的抗压屈服强度;SXY、SYZ和SZX分别为木材L-R、R-T和T-L三个平面的抗剪强度;N2和N3为木材抗压应变硬化时屈服面转移系数;n2和n3分别为木材横纹径向和切向抗压最终强度与屈服强度的比值;εo,1为木材顺纹纵向抗压时应变软化的门槛值,而εo,2和εo,3则分别为木材横纹径向和切向承压二次应变硬化(二次硬化)的门槛值。通用有限元软件目前均无法全面、准确定义木材本构关系,限制了木结构精细化有限元分析的发展。

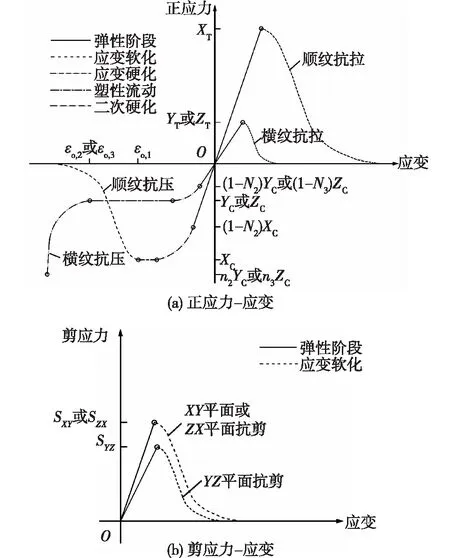
图10 木材各向应力-应变关系

目前研究中定义木材本构关系常用的方法是采用9个工程常数定义弹性性能,采用塑性应力-应变关系定义单方向的塑性性能；对于复杂的三向非线性应力-应变关系则需要考虑木材强度准则、硬化准则等,通过编制用户子程序实现本构模型的定义。徐博翰等[52]系统介绍了木材单轴、双轴以及多轴应力状态下的最大应力准则、最大应变准则、Hill屈服准则、Hill型强度理论、Tsai-Wu准则、van der Put强度理论和木材剪切强度理论。陈志勇等[53]将木材弹性应力-应变关系简化为正交各向异性,基于Yamada-Sun强度准则,通过引入损伤因子和弹性应变能, 建立了木材发生脆性破坏时的应变软化模型,通过设置初始屈服面和最终屈服面，并约束屈服面由初始向最终转移来描述木材应变硬化和横纹承压时的二次应变硬化。王明谦等[54]采用Hill屈服准则和Voce强化模型描述木材硬化行为,通过修正后的Hashin 破坏准则和指数型损伤演化模型控制木材受拉、受剪的损伤演化过程。Sun等[55]采用Hill屈服准则和修正后的Hashin破坏准则定义木材弹塑性损伤模型。

5.2 精细化有限元模拟

由于试验研究的局限性,斗栱的精细化有限元模拟是获取斗栱力学性能的重要手段。为了更符合斗栱实际受力情况,有限元模拟时需要充分考虑斗栱各组件的材料性能、接触状态和边界条件等。

张锡成等[56]建立了采用普通工程常数定义木材性能的普通斗栱模型和采用用户子程序方法定义木材本构的精细化斗栱模型,并对比二者在竖向荷载下的有限元模拟结果,发现精细化斗栱模型模拟的破坏形态和承载力曲线更加准确。潘毅等[57]采用ANSYS软件对计心造和偷心造两种构造形式的斗栱进行有限元模拟研究,斗栱间的木材接触方式采用刚体-柔体与柔体-柔体两类,木材接触面摩擦因数取为0.45。袁建力等[58]采用ANSYS软件建立斗栱实体模型,在斗与栱的接触面设置摩擦接触，模拟了斗栱摩擦-剪切耗能的作用。

董晓阳[59]通过ABAQUS有限元软件进行竖向荷载和水平低周反复荷载的数值模拟,得到歪闪斗栱节点在两种荷载形式下的破坏形态与完好斗栱节点类似,歪闪角度增大导致侧向刚度与耗能能力降低。钟永[60]采用ABAQUS软件对应县木塔中不同类型的柱头和转角铺作进行了有限元分析，得到了斗栱节点在竖向荷载作用下的荷载-位移曲线，归纳了不同斗栱的破坏形式、传力路径等。

5.3 斗栱有限元简化模拟

在对传统木结构建筑进行整体有限元分析时,现有研究采用多种方式对斗栱进行了简化模拟,如等效杆单元[61]、斜撑单元、半刚性连接单元等。姜绍飞等[62]探讨了古建筑整体结构分析的多尺度建模方法,对梁柱单元采用梁单元建模,对榫卯、斗栱采用实体单元建模,这种方式能够在计算精度和计算效率之间寻找到平衡点。刘妍等[63]研究了结构在竖向荷载作用下内力沿铺作中连接构件“斗”的连线斜向传递的规律,在整体结构模拟中将铺作简化为了斜撑与桁架的组合结构。王珏[64]通过分析斗栱结构的受力特点,利用刚度等效原则,提出了空间牛腿力学模型,并在应县木塔有限元模型中采用该模型模拟其斗栱。文献[65-67]将斗栱视为半刚性节点连接单元,利用现场实测和模型实验结果,采用Simplex方法反演推断半刚性节点平均刚度的范围。童丽萍等[68]在对整体建筑模拟时,采用Combine39单元定义斗栱半刚性特征,轴向采用线性弹簧模型、转动采用三折线弹簧模型进行模拟,并分别根据试验结果确定不同阶段的刚度。上述研究中对斗栱采用半刚性连接单元模拟斗栱的弹性和屈服阶段的刚度特征,但仍无法反映斗栱在地震作用下的滞回性能。

综上,斗栱的有限元模拟可以分为精细化模拟和简化模型模拟两种形式,精细化模拟中还存在木材非线性本构模型稀缺、接触定义不完善等问题;对斗栱在整体结构中简化模型的模拟还缺乏深入研究,没有考虑斗栱的恢复力特性对整体建筑抗震性能的影响。