数字建筑参数化设计中的几何学理论与方法

吴哲昊1 王天裕 张群力3 黄轩安3 潘润洲

(1.浙江省建筑设计研究院，杭州 310006； 2.杭州吉易科技有限公司，杭州 310000； 3.浙江新盛建设集团有限公司，杭州 310011)

1 数字建筑与建筑几何

“在建筑实践的现实世界中，数字技术已经渗入到方方面面，而设计师正是要负责数字技术在方方面面的联系。”——彼得.绍拉帕耶。数字建筑一般是指采用数字信息技术进行设计、建造及运维的建筑，数字化设计与制造中解决几何问题的三种重要的数学工具是计算机辅助几何设计、计算几何、微分几何。建筑几何学是数字时代建筑学结合复杂几何学进行多学科交叉的专业研究领域，2007年由奥地利计算几何学家赫尔穆特·波特曼提出这一概念，它是以计算机为技术载体，旨在解决数字化建模过程中复杂形体建筑设计建造问题，包括几何离散化和数值优化两方面特点。尽管建筑几何学属于跨学科的研究领域，受到建筑师、计算几何学家、结构工程师及数学家等不同群体的关注，但最终研究的仍是建筑形式的操作与实现。近年来，建筑几何学正逐渐成为数字化建筑领域的核心话题，它不仅是关联数字化设计与建造的“信息媒介”，更是关键的设计方法，以致力于探索与呈现几何规则、形式生成和建造逻辑之间的一致性[1]。

2 参数化与曲面内蕴几何

2.1 流形与参数化

流形的概念最早由黎曼提出，按黎曼的想法，排成一定次序的n个自变量看成一个动点，每一个自变量称为该动点的坐标，而动点的变换范围就是所谓的n维流形。流形的最重要的特性是具有局部坐标系，使许多几何、物理问题可通过坐标方法进行处理。流形是可以参数化的几何对象，在三维几何形体的创建、优化、表达的过程中，参数化是一种有效的工具。

2.2 曲面内蕴几何

度量和联络是微分几何中最基本的内蕴几何概念

(1)度量

曲面上由第一基本形式决定的几何，就是曲面的内蕴几何。曲面的度量是用曲面第一基本形式表达的，度量是内蕴几何概念。曲面的度量是曲面嵌入R3空间时由R3空间度量在曲面上诱导出来的一种黎曼度量。度量也称为距离函数，利用曲面的度量，就可以定义曲线的弧长、曲面的面积、两曲线的夹角、高斯曲率等内蕴几何量。

曲面参数化映射是计算机图形、图像工程中的重要的工具。它的任务就是在不同的曲面之间(局部乃至整体)建立图形图像几何信息无畸变、或部分无畸变的传输。具体可应用在纹理贴图、法向量贴图等方面[2]。数字建筑设计中可用于建筑表面蒙皮、幕墙风格排布等。

局部上当两曲面对应点上第一基本形式相等时两曲面存在等距(等度量)映射； 第一基本形式成比例时存在等角映射(共形映射)； 第一基本形式系数行列式(面元)相等时存在等面积映射。实现曲面参数化映射算法需要运用许多数学工具，但最原始的几何思想来自曲面度量概念。可根据对称的思想通过变换群分析此类几何问题，利用共形变换群(一般为有限群)研究曲面间的共形映射。利用等面积变换群(一般为无限群)研究等面积映射。曲面共形映射算法的理论基础来自共形几何，曲面表面积映射算法的理论基础来自最优输运理论。

(2)联络

比较曲面上两个不同点的几何量，得将两个点上的几何量放在同一点上才能进行，利用Levi-Civita平行移动是一个重要的方法。意大利数学家列维齐维塔(Levi-Civita)对弯曲空间上的几何做出了突出贡献，他发现的Levi-Civita平行移动为联络概念提供了几何上的解释。要在曲面上做几何，就要将平面上的直线、向量的平行移动的概念扩展到曲面上来。将曲面S上曲线C上的切向量场α(s)沿曲线的微分da(s)，按曲面的法线方向n投影到曲面S的切平面上，就得到了协变微分Da(s)。协变微分是一种线性微分算子有时也称为Levi-Civita联络，曲面上的Levi-Civita 联络系数可由曲面的度量张量导出，所以Levi-Civita联络概念也是曲面的内蕴几何概念。利用它可以建立曲面上的向量场不同点之间的保向量、保内积的一种同构关系。如果曲面上沿一条曲线的向量场的协变微分为零，我们称该向量场沿该曲线是Levi-Civita平行的。

实际上联络反映流形上的一种平行移动结构，是一种独立于度量的几何概念。利用联络可将流形上局部的微分几何与流形整体拓扑性质联系起来，对流形进行整体微分几何讨论。Levi-Civita平移的概念在弯扭斜交网格的控制网格线为测地线或分段测地线时，就可以看到其直观的几何意义。详见后续文章“弯扭斜交网格结构参数化设计中的几何学理论与方法”。平面上的等距曲线就是平行曲线，曲面上一般没有等距曲线和平行曲线的概念，只有测地等距曲线与Levi-Civita平行曲线的概念。

2.3 相伴曲面、法向映射曲面、法向等距曲面

相伴曲面Sx、法向映射曲面Sf、等距Sd曲面是计算机几何建模中的常用映射曲面[3]，它们是通过对两个曲面对比中来建立曲面及研究曲面之间几何特性的映射方法。设有两张曲面S和Sx，如果它们之间建立了点到点的映射关系，则称它们为一对相伴曲面。如果曲面Sf沿着曲面S的法向与S一一对应，称Sf为S的法向映射曲面。

当法向映射函数的距离等于常数c时，法向映射曲面Sf成为曲面S的等距曲面Sd(注：这是外在等距关系)，它们互为等距面。三种映射曲面按集合中的包含关系为：Sx⊃Sf⊃Sd。等距曲面与源曲面之间具有良好的几何对应关系，等距曲面或等距网格上，对应点共用同一法线。

高斯曲率是曲面上最重要的内蕴几何量，仅用一个数量就能反映出曲面上一个点的弯曲程度。曲面上任一点的高斯曲率数值上等于该点上曲面两个主曲率的乘积，几何上高斯曲率反映了该点曲面偏离平面的程度。当高斯曲率为零时曲面为平面(两个主曲率为零)或可展直纹曲面(一个主曲率为0)。曲面上高斯曲率大于零的点称为椭圆点，高斯曲率小于零的点称为双曲点。曲面做法向等距映射时，源曲面与等距曲面在对应点上的高斯曲率正负性不变； 对高斯曲率大于0的曲面，向凸方向映射时等距曲面的高斯曲率变小，向凹方向映射时等距曲面的高斯曲率变大，大小变化的公式可以用活动标架外微分法获得。

3 项目介绍

图1 运河亚运公园

图2 玉碂

图3 乒乓球馆外景

图4 乒乓球馆侧厅

图5 乒乓球馆比赛大厅

3.1 建筑设计及建筑表皮设计

本项目建筑轮廓的形成取自于良渚玉碂的形态，方圆求交。由内向外，中间圆形场地作为比赛大厅、空腔、侧厅。外围四个直角经过曲率优化处理成为圆润的卵状形体，与周围景观浑然一体。整个形体沿着高度方向在中部有一个小小的剪切变形，巧妙地设计出后方观景平台同时又增大了前方入口处的使用空间，现代工匠们利用数字信息技术精雕细琢出这一现代玉碂建筑[4]。

建筑表皮参数化设计，建筑形体表面是由若干张自由曲面组合而成的连通曲面，表皮造型主要由两部分组成。一部份是在曲面上按一定倾斜角排列的鳞片式仿铜平面铝板幕墙，另一部分是按斜交网格排列鳞片式棱形平面玻璃幕墙。棱形平面玻璃按排布逻辑渐变起翘，两种幕墙之间通过变换表皮曲率形成的腰带鼓包进行过渡。整体上两种幕墙通过虚实对比、动静结合形成完美的视觉效果。白天，阳光照射下铝板熠熠生辉，幕墙整体亮度分布随阳光与铝板平面夹角大小变化，自然地反映了建筑外轮廓上空间曲率变化。夜晚，当月亮在空中升起，月光撒落大地，每一块棱形玻璃上都会折射出一个月亮，令人想起春江花月夜中诗句“滟滟随波千万里，何处春江无月明”。整个建筑表皮设计给人以极致雍容华贵感觉，远处望去，弯曲形体表面构画出了一幅行云流水、鱼跃龙腾的图案。

3.2 结构设计

整体结构由外围护结构、内部混凝土框架结构、屋顶自由曲面空间网架结构组成。其中外围护结构由两部分组成，一部分是阳极氧化铝板幕墙区域，底部混凝土型钢斜柱加上部自立式钢桁架，另一部分是玻璃幕墙区域，弯扭斜交网格结构。两部分结合处布置了格构式钢柱用于转换和传递两部分结构之间相互作用。内部结构为钢筋混凝土框架结构，在内外两圈空腔的墙体部位，用圆柱坐标系各按每十度布置一个框架柱，内外圈框架柱之间以及环向框架柱之间布置混凝土梁板结构形成空间框架结构。屋顶结构为自由曲面空间网架结构，网架底部共有36个支座，分别安装在36个混凝土柱顶部，其中外圈26个，内圈10个，基础采用混凝土钻孔桩基础。

图6 结构系统

4 建筑的基本几何控制系统

4.1 基本几何控制系统组成部分

数字建筑领域的领军人物邵韦平教授曾对建筑几何控制系统做出如下定义“设计师会在设计控制过程中对所有与几何定义相关的信息、数据进行系统的描述和表达，而这些处理后的几何信息具有直接与建造对接的能力，以达到全过程精确控制设计、深化、加工、安装的目的。将这类描述几何定义，限定几何关系的信息、数据统称为几何控制系统。其表现在计算机模型中为具有具体坐标和特性的点、线、面所组成的数据系统。”建筑外形轮廓确定之后，对于复杂形体的建筑还要用几何方法建立一套有效的基本形态控制系统[5]，称为基本几何控制系统。

本工程基本几何控制系统由三部分组成：a)一个R3中的欧氏坐标系(原点设在比赛场地中心，标高为正负0.000处)作为建筑整体坐标系； b)不同楼层的平面轴网关系； c)由若干张自由曲面组成的组合曲面。该组合曲面为建筑几何形体外边界的控制曲面，是该基本几何控制系统中最重要的一个组成部分，我们称为基本控制曲面。以它为源曲面利用R3中法向等距曲面族对弯曲空间区域进行有序、等厚、弯曲映射(剖分)。对边界曲面内侧空间区域进行参数化，得到一个流面场。将空间区域用一张张等距曲面填满，使得每一点上都有一张且仅有一张参数曲面通过。这些空间区域经过法向等距参数化划分后，便可利用流面场对各弯曲区域内的弯曲、弯扭构件进行参数化布置。

4.2 建筑主系统与建筑次系统

总的建筑系统是由建筑结构系统、建筑幕墙系统、建筑装饰系统、建筑机电系统、建筑设备系统、赛事系统等组成。这些系统需统一规划、有组织、分层次、有序的布置在建筑内部彼此相邻的空间中。按照实际建造过程，我们将建筑结构系统作为主系统，其它系统作为次系统。因为从结构受力而言幕墙系统的龙骨、装修系统的龙骨、机电及设备系统的支架、吊架等次结构(非结构性构件)都是依附于主体结构上的。必须等主体结构布置好以后才能考虑它们的连接布置。所以首先要确定主系统的几何控制系统，然后按次结构与主体结构的连接关系及各次系统中几何形体的生成逻辑衍生出各次系统的几何控制系统。

4.3 由建筑主系统的几何控制系统衍生建筑次系统的几何控制系统过程简单介绍

(1)外围非线性建筑主系统的几何控制系统

根据各设计专业的协调结果将基本控制曲面沿曲面法线向室内作等距映射，其中阳极氧化铝板幕墙处距离为500，玻璃幕墙处距离为350。映射后得到的曲面组合作为建筑主系统的控制曲面。其中阳极氧化铝板幕墙处的钢结构为水平面内弯曲的钢梁、竖直面内弯曲钢柱组成的钢桁架，按结构平面布置用水平面和竖直面与主系统的控制曲面求交就得到它们的控制网格曲线。玻璃幕墙后面的钢结构是弯扭斜交网格，所以还要在控制曲面上建立起弯扭构件定位的网格曲线。弯扭斜交网格的几何形体较为复杂，光有控制曲面、控制网格还是无法建立高质量的几何模型。需要利用光滑曲面、曲线上的微分结构以及利用曲面上任意点上法线及曲线上任一点上切线的唯一性，在网格线上建立起活动标架场，才能完整建成该处建筑主系统的几何控制系统。(详见第5章中相关内容)

(2)建筑主系统几何控制系统衍生建筑次系统几何控制系统

对于几何关系相对简单的建筑次系统几何控制系统可以由建筑主系统几何控制系统衍生得到，衍生的过程有点类似施工过程中的二次放样。一个是在虚拟的电脑模型中实现，另一个是在建筑实体上实现。以铝板外幕墙背后室内的建筑装修系统(也称为内幕墙)为例作简单介绍，该系统由水平面内的弯曲主龙、竖直面内弯曲的次龙、铝板组成。内幕墙完成面S*与主体结构钢柱室内方向表面所在控制曲面S之间为法向等距曲面关系。将S向室内的法向等距映射5公分就得到S*。用等高的水平面(间距约2.5m)与S*相交，得到水平面内的曲线就是水平主龙的定位轴线。再用竖直面(该竖直面的水平面投影线垂直S与楼层平面的交线，间距约1.2m)与S*相交得到竖直面内的曲线就是竖向次龙骨的定位轴线。这样我们就完成了一个由建筑主系统的几何控制系统衍生出了一个建筑次系统几何控制系统的过程。类似弯扭斜交网格上玻璃幕墙系统(龙骨及玻璃)的几何控制系统也可用建筑主系统的几何控制系统直接衍生得到。(详见第5章中相关内容)

对于几何关系复杂的建筑次系统几何控制系统例如铝板幕墙的几何控制系统要用建筑基本几何控制系统联合建筑主系统的几何控制系统共同衍生出来。(详见第5章中相关内容)。

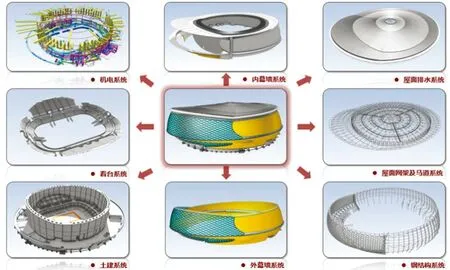
图7 建筑子系统集

5 建筑外围护系统参数化设计

5.1 建筑外围护系统

本工程建筑外围护系统按铝板幕墙和玻璃幕墙分为两个部分，一部分为阳极氧化铝板幕墙区域，该区域外围护系统由内到外含有三层分别为内装修系统(装修表皮加龙骨)、钢结构系统(弯曲的钢桁架)、铝板幕墙系统(铝板加二道龙骨)。它们布置在由四张等距曲面分隔的三个弯曲的空间区域中。而两个相邻区域的交界曲面，就是基本控制曲面S的某一个等距曲面。所有构件由控制曲面上的控制曲线所定位。另一部分为玻璃幕墙区域，该区域外围护系统由内到外含有二层分别为钢结构系统(弯扭斜交网格[6])、玻璃幕墙系统(玻璃加龙骨)。它们布置在由三张等距曲面分隔的二个弯曲的空间区域中。所有构件由控制曲面上的控制曲线所定位。利用了同一点上控制曲线、控制曲面的线性结构，在选定的控制点集上分别建立局部的三维欧氏坐标系对构件的正截面进行欧氏几何操作与布置。由于两张等距曲面上对应的网格也保留了等距的性质，所以通过这套由控制曲面、曲线构造的几何控制系统，就可以对其中所有构件按结构层次、结构布置、连接方式进行空间定位。

5.2 玻璃幕墙区域钢结构及幕墙的参数化建模

(1)曲线网格优化

曲面上网格的最优控制指标是根据造型设计要求所确定，通常情况下，曲面上一个良好的造型网格应该具备以下几个基本控制条件，曲线的光顺性、网格大小、夹角的均匀性、良好的渐进性和对复杂曲面的适应性、可进行参数化调控(网格曲线为等参曲线、等值曲线)。用RhinoScript编写脚本或RhinoGrasshopper参数化建模，“按最优控制指标设立奖罚函数进行迭代计算，条件判断直到满足精度，最后给出网格图形”。因篇幅关系不在此展开，详见后续文章“弯扭斜交网格结构参数化设计中的几何学理论与方法”。

图8 控制网格与控制曲面

图9 壳与镂空壳

(2)弯扭斜交网格结构

可以用控制曲面的法向等距曲面建立等厚壳模型，然后在三维壳体上按控制网格要求镂空中间棱形部分得到弯扭斜交网格的模型。虽然这种模型的外表面更符合建筑设计的要求，但是在制作过程会遇到困难。这种模型的前后两个表面与控制曲面一样为自由曲面，无法展平，只能用在减料加工成型的制作工艺上。“建筑几何学提供的工具可以将标准数学模型转化为适合建筑应用和制造的形式，这个转化过程被称为合理化过程”——赫尔穆特.波特曼。采用矩形(环形平面)扫掠成型的方法得到的模型，四个表面都是可展的直纹曲面，刚好符合用钢板做弯扭板件然后组装成弯扭杆件，最后拼装成弯扭斜交网格的制造工艺。

(3)用控制曲面、曲线上线性结构建立活动标架场

本工程利用控制曲面、曲线上的线性结构建立一批专用活动标架。弯扭斜交网格的每根杆件可以由一个矩形边框，将其中心约束在控制曲线上，矩形平面的两个主轴约束在曲线法平面上的两个标架矢上，沿曲线扫掠成型。

设P为 曲线L上一个点，L为曲面S上的一条曲线：P∈L⊂S，利用P点曲线L的单位切向量作为P的活动标架的第一基矢r1，曲面S的单位法向量作为P点的活动标架的第二基矢r2，r1×r2=r3作为P的活动标架的第三基矢。即得P点的活动标架(P；r1，r2，r3)。利用该标架中的平面直角坐标系(P；r2，r3)就可以将弯扭构件的正截面布置在R3空间中。其中矩形的两个主轴分别与r2，r3重合。

具体步骤：建立控制曲面上的斜交曲线网格； 对每条网格线按弧长等分； 在每个分点上建立活动标架； 在每个标架上布置杆件的截面； 因篇幅关系不在此展开，详见本文的后续文章：弯扭斜交网格参数化设计中的几何学理论与方法。

6 玻璃幕墙的龙骨及玻璃的排布

6.1 玻璃龙骨建模

弯扭斜交网格区域的玻璃幕墙龙骨也可以利用弯扭构件的活动标架来建立三维模型。这是因为基本控制曲面及曲面上的控制网格经法向等距映射后，仍然保留了对应的几何关系，详见图11。

图11 带龙骨的弯扭构件

6.2 玻璃的裁剪与排布

前面已对曲面上曲线的测地等距线、曲线的Levi-Civita平行曲线进行了讨论，在三维建模时，在满足设计精度的前提下可以利用(offset)偏移曲线来代替“平行”或“等距”曲线。将等距曲面上的所有控制网格线向两侧棱形区域偏移75得到偏移曲线，然后这些偏移曲线两两求交，删除棱形区域以外的部分曲线和曲面，得到一块块独立的棱形曲面。每一个曲面棱形上有4个角点，用其中的1#、2#、3#点作一个平面(该平面并不其中是某一个点的切平面)，4#点一般情况下位于平面的下方，但也有极少数位于平面上方。用4#点上控制曲面的法线与平面相交得到4′#点，这样我们就可以利用1#、2#、3#、4′#点建立一个棱形的平面，其各条边均为直线。其中的4′#点翘曲脱离控制曲面，其它三个点都位于在曲面上。对于前面提到的极少数情况“4#点位于平面的上方”就要将此棱形平面玻璃沿平面的法线方向，向外平移保证4#点位于平面的下方，详见图12～13。

图12 平板玻璃4#位起翘

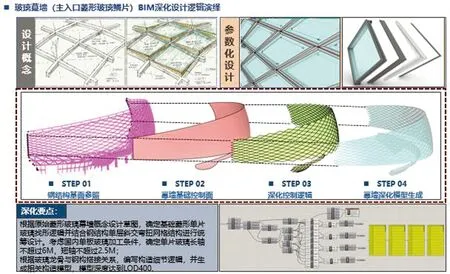
图13 玻璃幕墙

7 阳极氧化铝板幕墙区域的建模

7.1 曲面形钢桁架系统

阳极氧化铝板幕墙通过连接件、主次龙骨与后方的曲面形钢桁架系统连接。水平次龙骨与斜向主龙骨连接，斜向主龙骨再与后方的曲面形钢桁架系统连接，钢桁架柱在竖直面单方向弯曲，桁架梁在水平面单方向弯曲。它们的定位及建模较为简单，这里不再进行讨论。

7.2 铝板幕墙排布、裁剪

幕墙的排布风格可以通过控制曲面上的纹理贴图来实现。纹理贴图技术在数学上等价于从曲面到平面区域的一个光滑双射，在计算机图形、图像工程中称为曲面参数化问题。

本工程利用控制曲面上离散线性结构直接进行排布。控制曲面的每一个点上有一个切平面(由该点的全体切向量组成)，由曲面及其曲面上所有切平面构成的几何对象称为切丛[7]，曲面为该切丛的底流形。选择曲面上有限多个点及这些点上的切平面，得到一个离散的切丛Q。利用Q可以排布、裁剪出整个幕墙阳极氧化铝板的布置风格。

铝板幕墙的龙骨以及铝板在控制曲面上的排布、裁剪方法通过曲面的边界曲线分析，整张控制曲面有上下左右四条边界曲线，其中上边界曲线的弧长比下边界曲线的弧长短。将上下边界曲线都作n等分，根据倾斜角的要求用曲面上的测地线连接上下边界曲线上的对应分点。这样就得到了所有铝板和龙骨的定位曲线(选取其中一条作为基准线R)。曲面上两条定位曲线之间水平方向曲线，由水平面与曲面S的求交产生，水平方向曲线弧长变化的规律是随标高增大而慢慢减小。所以每块铝板的宽度也是按变化取值。底部区域的铝板宽度约为2.0m，顶部区域的铝板宽度约为1.8m。利用基准线R，将一个矩形平面的左上角的点约束在曲线R上的A点，在A点做S的法线和切平面，再用过A点的水平面与切平面求交，得到切矢r1，在切平面上将切矢r1绕A点旋转90度复制得到切矢r2。这r1和r2就定位了铝板的两条边线，在切平面上再利用平移复制方法得到铝板另外的边线(详见图14)。还可以在法线方向挤出铝板的厚度。然后沿着基准线R往上，确定第二个矩形平面的左上角在R上的定位点B，在B点建立S的切平面和法线，依次类推就可完成第一列矩形的铝板排布。然后布置第二列上的铝板，该列的水平面比前一列的水平面对应的铝板要抬高150，保证满足上下两块铝板间覆盖距离要求。而铝板的宽度最下面约为2m(比定位曲线间距宽出约200)，往上排与定位曲线的间距变化的规律一样，随标高增加而慢慢减小)，保证满足左右两列铝板之间的覆盖距离要求。在确定矩形铝板排布逻辑及原则后，利用RhinoScript编写脚本或使用RhinoGrasshopper参数化建模，RhinoGrasshopper具有内置的微分几何方法，根据控制点法线和切平面，确定各个板件位置和倾斜角，还可通过软件对不同规格的铝板排列情况随机编号。通过数据查验和渲染观察比较，平衡几何误差和美学诉求关系(详见图15)。

图14 每块铝板定位于切平面坐标系的第4象限

图15 曲面离散切丛上铝板的排布组

7.3 铝板幕墙的龙骨系统

根据前面的铝板排布可知，铝板的控制线系统为基本控制曲面上斜向排列的测地线组成，次龙的控制线系统为水平面与基本控制曲面交线组成。因为铝板是在基本控制曲面上排布的，将基本控制曲面和其上面铝板的定位曲线族(测地线)沿曲面法向往室内方向等距映射45公分，就可衍生出铝板

幕墙主龙骨的控制曲面和控制曲线系统。这些主龙是连接在主体结构上的，所以再次利用曲面的法向

映射，将定位曲线族向室内方向映射5公分(45+5= 50)通过它们与主体结构控制线的交点，就能确定幕墙主龙与土建结构的连接位置。

通过主龙的控制曲面与主龙控制线我们可以对主龙(空间曲线)弯扭构件建模。通过基本控制曲面与次龙控制线我们可以对次龙(平面曲线)弯曲构件建模。细部设计上，通过RhinoGrasshopper模型的细节推敲、尺寸数据检查以及构造详图的绘制。综合三方面工作，对原有模型参数进行调整修正。对钢结构、主龙、次龙、突包、幕墙转角、幕墙周边节点等方面，参数化设计均发挥了重要作用。

图16 整体主龙与铝板

8 建筑屋盖系统的参数化设计

屋顶结构采用自由曲面空间网架结构[8]，构件为圆杆、球节点。网架定位与建模(文章篇幅所限)不在此进行讨论，网架顶上由顶撑、主檩(径向布置)、次檩(环向布置)组成金属屋面的龙骨系统。屋面为直立自锁边铝镁锰板金属屋面。

8.1 直立自锁边氧化铝镁锰金属屋面建模

直立自锁边氧化铝镁锰金属屋面板建模，对直纹曲面顺屋面坡度(泛水)方向进行模数化细分，正好利用了直纹曲面上的测地线(直线)局部短程性质进行有效的排水。屋顶控制曲面为可展直纹曲面，由5个环形区域组成。利用等高线族对其进行分析，可以发现，屋面顺泛水方向还带有脊谷形变化。屋顶控制曲面上的金属屋面系统建模逻辑， 金属屋面直立自锁边铝板建模策略与步骤：

1.将一块直立自锁边铝板两条长边在曲面上对应的两条定位曲线L和L′按弧长各等分为n段，得到n+1对等分(定位)点，A，A′；B，B′……。测量出各段直线AA′，BB′，……的长度，及各段长度相对于端部长度AA′的比值。在一个平面上将每一个直立自锁边铝板的横断面(为组合曲线)按比例缩放复制好。

2.将这些截面移动到曲面上相应的定位平面上，以下有两种方法来确定定位平面：

方法2：在曲面上用测地线连接A点和A′点，然后求出测地线AA′中点A″，在点A″上求曲面的n″法向量，由直线AA′和n″建立平面。在该平面上布置该片直立自锁边铝板的横断面(组合曲线)。

3.将各段的横断面一一对应考入各自的定位平面中，两侧的直立自锁边不一定落在定位点的法线上，以定位点为旋转中心将其旋转到定位曲线的法平面内并与曲面法线重合。然后将各曲线段固接，得到一个空间组合曲线(注意：原来是平面组合曲线)。

4.对这些空间曲线进行放样生成LOFT曲面。详见图18。

图17 屋面排水分析

图18 直立自锁边建模

9 结语

本文从几何学观点讨论了建筑设计中的参数化方法[9]。阐述了几何学作为建筑参数化设计底层理论的重要性。参数化设计是利用计算机为建筑设计提供形体控制、分析、细化、数据化等系列化服务。参数化建模一般应用在优化技术上，通过将模型参数化、优化过程中不断对其进行迭代而求出最优解。建模时采用参数(变量)，通过简单的改变模型中的参数值就能建立和分析新的模型。本工程参数设计总结如下：始终按几何学理论建立逻辑关系，从初期的几何形体描述、中后期的深化建模和各部分细节点推敲优化都是对建筑从整体到细节的基于对几何学关系与美学特征把握下的操作。对控制参数进行合理的选择，区分建模过程中的可调参数、固定参数、与常数是明确和简化参数化模型的关键所在，曲面内蕴外在的几何是参数化设计时建立逻辑关系的基础。注重把握生成思维、曲面设计、逻辑优化、算法研究、数据结构、工程对接这6个环节[10]。最后借助于几何造型软件如RhinoScript或RhinoGrasshopper进行参数化建模。