广义有限差分法在含阻抗边界空腔声学分析中的应用1)

陈增涛 王发杰,†,2) 王 超

∗(青岛大学动力集成及储能系统工程技术中心,青岛大学机电工程学院,山东青岛266071)

†(青岛大学多功能材料与结构力学研究院,山东青岛266071)

引言

目前,有限元、有限差分和边界元法作为空腔声场模拟计算中的主要方法,在汽车发动机传热或车内噪声控制、封闭管道噪声声场等方面均有广泛应用.然而对于一些多维复杂几何域问题,合理有效的模拟计算很难准确实现.不同于以上依赖网格的数值计算方法,无网格法通过节点信息建立插值基函数,插值基函数不依赖于节点之间的有序拓扑链接,因此相对于传统方法不会受到网格划分的约束.近年来无网格方法的研究受到了高度重视,成为目前科学与工程计算中的研究热点之一[1-6].

根据插值基函数的类型不同,无网格法可分为边界型[7-8]和区域型[9-10]两大类.边界型无网格法保留了降低所求问题维度的优点,并且避免了复杂的奇异和近奇异积分的计算.近年来,边界型无网格方法引起了广泛的关注,主导方法有边界节点法[11-12]、基本解法[13-14]、边界无单元法[15]、奇异边界法[16-18]、正则化无网格方法[19]等.以上方法均在多种领域成功运用并取得了不同程度的成功,但是仍存在一些决定性的问题.例如,该类方法在实际工程中的应用范围[20]很大程度上会受到插值基函数的影响.

相对于边界型无网格法,区域型无网格方法摆脱了插值基函数的约束,所以对各种偏微分方程初边值问题具有普遍适用性,应用领域更为广泛.现如今,比较常用的区域型无网格法包括光滑粒子水动力学法[21]、扩散单元法[22]、无单元伽辽金法[23-24]和广义有限差分法(Generalized Finite Difference Method,GFDM)[25]等.其中,广义有限差分法是一种最近发展起来的新型无网格方法,已被成功应用于生物传热分析[26]、薄板弯曲问题[27]、分数阶反常扩散[28]、热弹性[29]和反问题[30]等领域.

广义有限差分法不仅保留了有限差分法把微分方程转变成差分方程的优点,而且引入了点簇的概念,在模拟复杂的几何形状问题时十分具有优势.除此之外,广义有限差分法只需要在物理域内随机布置一组节点,通过相邻节点之间的关联得到中心节点的函数值,节省了有限元和边界元法中费时费力的网格划分及数值积分,大大节省了数据准备的时间,在人工越来越昂贵的情况下,这也是非常重要的优势.

本文首次将广义有限差分法应用于含阻抗边界空腔声学问题的分析和模拟,建立了空腔声场问题的广义有限差分法数值离散格式.数值试验测试了经典的二维车腔噪声模型和三维空腔声学模型,并与有限元法的数值结果对比来验证该方法的有效性、精确度和稳定性.本工作为含阻抗边界空腔声学问题的仿真提供了新的、简单高效的计算工具,也拓展了广义有限差分法的应用领域.

1 空腔声场问题的基本理论

声波在传播过程中会不断被拉伸和压缩,动作非常快,质点间来不及进行热交换.因此声波的传播过程可被看成是绝热过程[31],其热力学方程为

其中,p0是空气静态压强,ρ0为微元体初始密度,γ 是空气的比热比,将式(1)对时间求导可得

推导可以得到在x方向上的一维声学方程

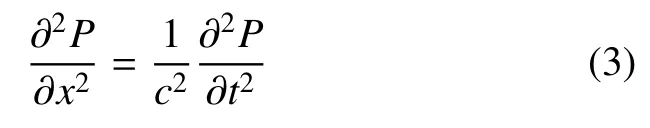
结合x、y和z三个方向的一维声学方程,可以得到三维系统的声学运动方程

在上式中引入拉普拉斯算子∇2

则式(4)可以写成

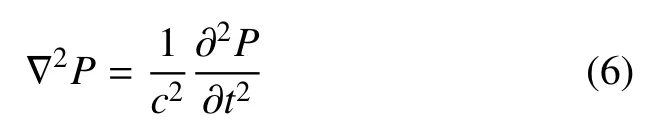
对简谐激励稳态声场,利用变换P(x,t)=p(x)eiωt,可将式(3)中的时域声场方程变换为频域声场方程,即Helmholtz 波动方程

其中,K=ω/c称为波数,ω 为圆频率,c为声速.上述方程描述了频域内稳态声场在空间的分布规律.对于二维和三维声场分布,同理可得到与(7) 式相同形式的控制方程.声压与简谐声波的振动速度关系式为

在已知边界条件下,可定量对其进行求解.声场有如下几种边界条件:

(1) 狄利克雷(Dirichlet) 边界条件,即声压边界条件

(2)黎曼(Neumann)边界条件,即速度边界条件

(3)洛平(Robin)边界条件,即声阻抗边界条件

在式(9)∼式(11)中,pD是边界处声压值,An是声导纳系数.

2 广义有限差分法的基本理论

根据广义有限差分法(GFDM)计算空腔声场问题的基本理论,对求解区域布置节点进行离散,其方法是基于移动最小二乘法与泰勒展开.首先在整个计算区域内布置N=ni+nd+nn+nr(ni表示内部节点数目,nd,nn,nr分别表示Dirichlet,Neumann 和Robin 边界所对应的节点数目) 个节点,再将每个节点上的偏微分项转换成由子区域内各节点物理量与权重系数乘积的线性累加.以二维问题为例,对区域内的第i个节点而言,选择m个支撑点(邻近点),形成一个子区域,如图1 所示.

图1 广义有限差分法配点布置示意图Fig.1 Schematic diagram of GFDM

通过观察上述各式可以看出中心节点处的微分项可以变换为由子区域中各点上的物理量与权重系数乘积的线性累加.由此可知,广义有限差分法的核心思想是将第i点上的微分量用对应子区域内支撑点上的物理量线性权重累加表示,使所有内部点满足控制方程式,所有边界点满足边界条件,形成一个大型的稀疏线性方程组,对该方程组求解即可得到计算区域内全部点上的物理量.

(1)对于计算区域内部节点(xi,yi),i=1,...,ni,其上的物理量必定满足声学控制方程.由式(20)可知,只需提取相应的微分项,然后将线性组合的方程式代入控制方程,则

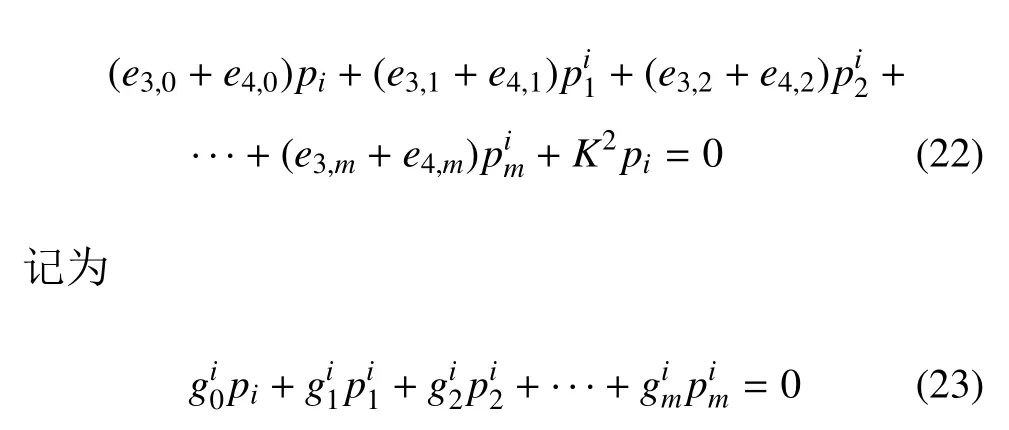
从而得到最终的计算结果.

从上述数值实施过程中可以看出,GFDM 与传统的有限差分法十分类似,方程(32) 中的系数矩阵C为稀疏矩阵.另一方面,从形成最终线性方程组(32)的过程可以观察到,系数矩阵C是一个N行N列的方阵,而每一行最多仅有m个非零元素,这里N为计算区域内全部节点的个数,m为局部支撑节点数目.显然,m远小于N,因此方程组(32)是一个稀疏线性方程组.由此可见,与其他具有稠密矩阵方程的数值方法相比,GFDM 能够非常有效地分析高维和复杂几何形状的问题.

3 数值算例

为了验证广义有限差分法求解含阻抗边界空腔声学问题的有效性和可行性,现针对二维简单声腔结构和二维汽车驾驶舱以及三维声腔模型进行研究,重点探讨无网格法和有限元方法求解不同频率下声腔的声场分布情况.需要指出的是,在下面所有算例中,腔体内的介质均为空气,其密度ρ 为1.225 kg/m3,声波在空气中传播的速度c为343m/s,为节省篇幅,这些参数在下述算例中将不再具体定义.除特殊说明外,数值结果均在i5-5200 CPU@2.20GHz,内存4GB的计算机上运算所得.文中有限元结果均来自于有限元仿真软件COMSOL Multiphysics 5.4.

为了评估数值误差,采用最大相对误差(MRE)和均方根误差(RMS E)

其中NT是测试点的数量,pexa和pnum分别表示第i个测试点的解析解和数值解.这里,除特殊说明外测试点均为区域内部节点.

3.1 混合边界管道声场分析

现求解如图2 所示的二维矩形声腔结构,其长度L=1.0 m,宽度H=0.2 m,在A 端口边界给定Neumann 速度边界,法向速度vn=0.01 m/s,管道B端口是刚性壁,其他边界为声学硬边界条件.

图2 管道声学模型Fig.2 Pipe acoustic model

管道声压的精确解为

按照GFDM 求解此类问题的前处理过程,首先将该模型离散成17 996 个点,即总节点数N=17 996,计算时选用的内部支撑点m=12.图3 给出了当频率分别为400 Hz 和600 Hz 时,计算得到管道底部轴线上的声压分布.分析图3 声压曲线图可知,不同频率下GFDM 所得数值解与解析解均非常吻合.

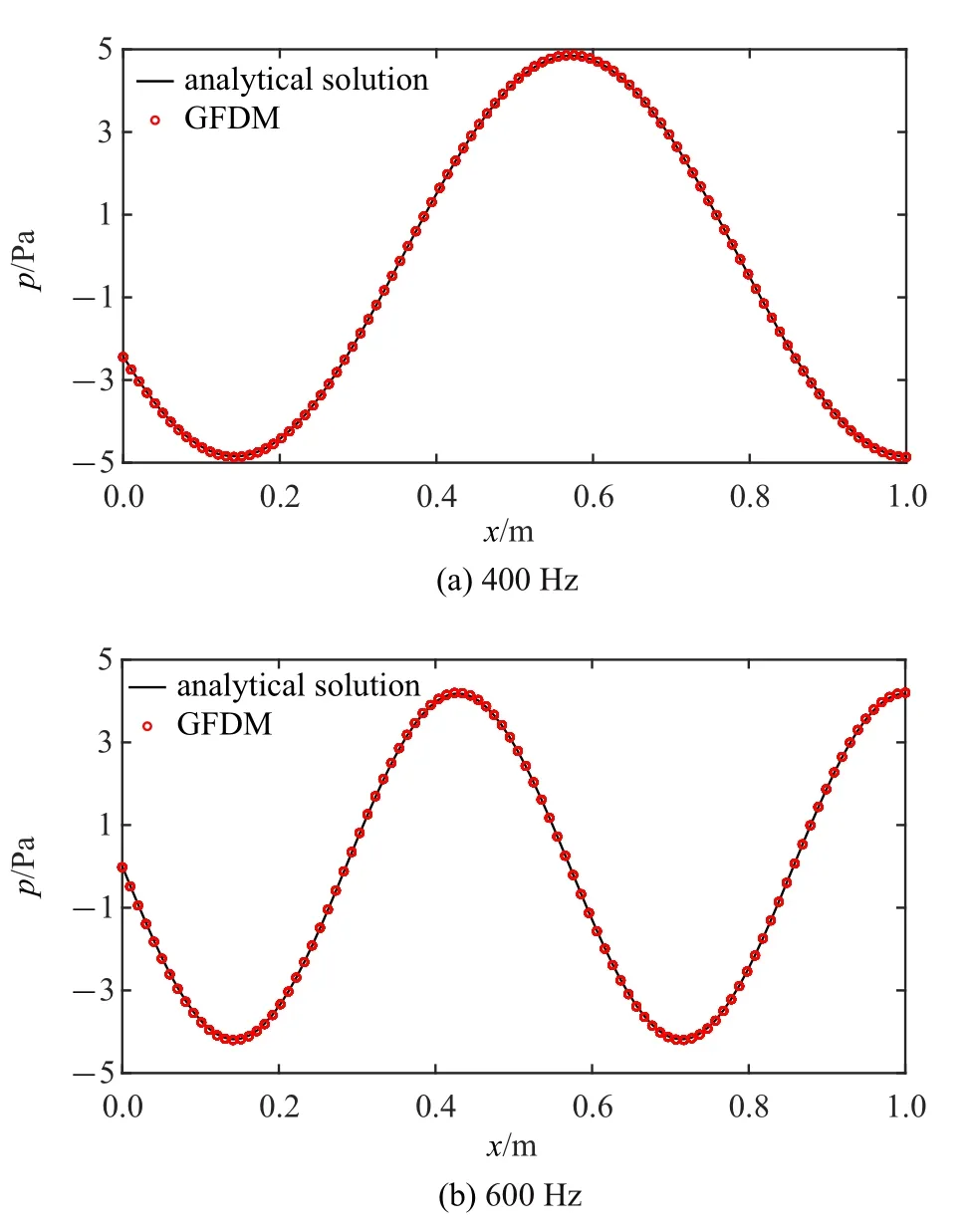
图3 不同频率下管道底部轴线声压分布Fig.3 Distributions of sound pressure at the lower boundary under different frequencies

为了检验GFDM 中总节点数目和内部支撑点数目对计算结果的影响,研究了频率为400 Hz 时,不同内部支撑点数目和总节点数目对计算方法的影响.分析表1 计算所得的数据可知,总节点数N=17 996时,随着内部支撑点数目m的增大,GFDM 的计算最大误差和均方根误差随之变小,也就是此方法的计算误差随之收敛.观察表2 数据可知,在内部支撑点数m=12 时,随着模型的总节点数目的增加,计算结果的最大误差和均方根误差都会随之减小.可见,模型离散的点数越多,GFDM 的计算结果越精确,表明算法具有较好的计算精度和收敛性.

表1 总节点数N=17 996 时,不同支撑点数下的最大相对误差、均方根误差和计算时间(CT)Table 1 When N=17 996,the MREs,RMS Es and calculation time(CT)under different number of supporting nodes

表2 局部支撑点数为m=12 时,不同总节点数下的最大相对误差、均方根误差和计算时间(CT)Table 2 When m=12,the MREs,RMS Es and calculation time(CT)under different number of total nodes

为从数值上分析最大计算频率与节点间距(对应于离散点数)之间的关系,我们选取不同的频率和节点间距∆h=,将GFDM 计算所得的RMS E误差曲面绘制于图4(a)中.观察图中误差分布情况,我们可以清楚地看到计算误差随着频率和节点间距的同时增大而增大.为更好地分析最大计算频率与节点间距之间的规律,图4(b) 给出了对应的二维误差分布情况,图中红色圆点表示误差大小为RMS E=1.0×10−2的位置.通过曲线拟合的思想,得到了误差为RMS E=1.0×10−2所在点构成的一条拟合曲线(图中绿色曲线):f=35·∆h(−0.65).至此,我们便得到了一个估计最大计算频率的经验公式

需要指出的是,根据经验公式(38),在保证计算精度为RMS E1.0×10−2的情况下,我们可以轻松地估计出能够计算的最大频率.这里仅从数值的角度获得了一个计算频率与节点间距关系的经验公式,理论上获得准确的估计公式目前仍面临巨大挑战,还需进一步研究和探索.

图4 不同频率和节点间距下GFDM 所得计算误差RMS E 的分布Fig.4 Distribution of RMS Es under different frequencies and node intervals

为了考察GFDM 对高频声学问题的计算精度和计算稳定性,我们选取计算频率为20 000 Hz,分析其计算结果.通过经验公式(38),我们能够估计出计算频率为20 000 Hz 时取得良好精度(RMS E<1.0×10−2)所需的节点间距为∆h=0.000 055 m,此时,该模型大概需要66 000 000 个离散节点.受工作条件和计算机内存的限制,想要模拟如此大规模的声学问题,仍然面临巨大挑战,即便使用另外一台较大内存的计算机(i7-6700 CPU@3.40GHz,内存16 GB)进行模拟,4 999 996 个节点(节点间距∆h=0.000 2 m)就已经达到了计算机的内存极限.在该离散节点数目下的计算结果如图5 所示,可以看出GFDM 所得结果与精确解(exact)十分吻合.计算过程花费了3990.333 s的计算时间,计算误差为RMS E=0.087 362.另外,从图5 中可以看出,高频问题对应的声压波动非常剧烈,这类问题的精确模拟对大多数数值算法来说都是比较棘手的,上述数值结果表明GFDM 能够有效模拟高频问题,对该类问题具有较高的计算精度和计算稳定性.

图5 频率为20 000 Hz 时管道底部轴线声压分布Fig.5 Distributions of sound pressure at the lower boundary under f=20 000 Hz

3.2 二维车腔声场分析

在整车的概念设计阶段,车内声腔可近似地被看作为棱柱体,因此可将其简化为二维模型进行噪声分析.图6 所示为某车简化之后的车内声腔模型,其水平方向的长度L=3.41 m,竖直方向的高度H=1.21 m,相关条件已在图中标示[35].腔体内部介质为空气,由于发动机振动激励引起的噪声占整车噪声的绝大部分,因而在汽车的前围板上施加一Neumann 边界条件,其振动速度为0.01 m/s.此外,我们也在乘员舱的顶部cd 处施加一Robin 边界条件以模拟内饰材料的阻尼,这里声阻抗值为413 Pa·s/m3.在算例分析中,选取底部轴线ab 上的声压数据进行研究.图7 给出了模型的GFDM 节点分布示意图.

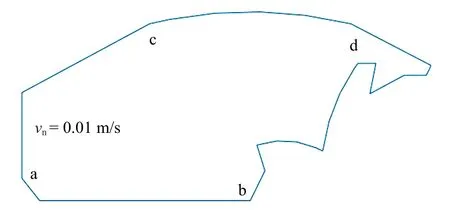
图6 具有阻抗边界条件的二维车腔模型Fig.6 A two-dimensional car cavity with impedance boundary

图7 车腔的GFDM 节点分布Fig.7 Distribution of nodes on the car cavity

车内噪声按其频率高低一般可分为低频噪声(1 ∼200 Hz)、中频噪声(200 ∼500 Hz) 和高频噪声(>500 Hz).在实际驾乘过程中,接触最多的是中低频噪声.因此,我们首先分析了低频(f=200 Hz)时的声压分布,为验证算法的有效性和准确度,我们把细密网格下有限元(FEM)的数值解作为参考解.采用有限元法进行声学数值计算时,为了保证其结果的准确性,需满足声学“经验法则”,即最小波长内至少有6 个网格单元.在接下来的计算分析中,首先将汽车腔体模型在有限元软件中划分为43 480 个三角形单元,网格尺寸为0.01 m,即每波长内包含171个网格单元.使用GFDM 计算时,将算例模型离散成11 558 个离散节点,即N=11 558,节点间距为0.02 m.图8 给出了频率较低f=200 Hz 时,内部支撑点数m=12,总节点数N=11 558 时声腔模型内声压分布云图.从图8 声压分布云图可以看出,即使在较低频率下,FEM 和GFDM 计算的结果整体上吻合良好,表明了GFDM 使用低于有限元求解经验法则的节点数就可以获得比较理想的求解精度,也体现了该方法在降低计算内存消耗和提高数值计算效率方面的潜能.

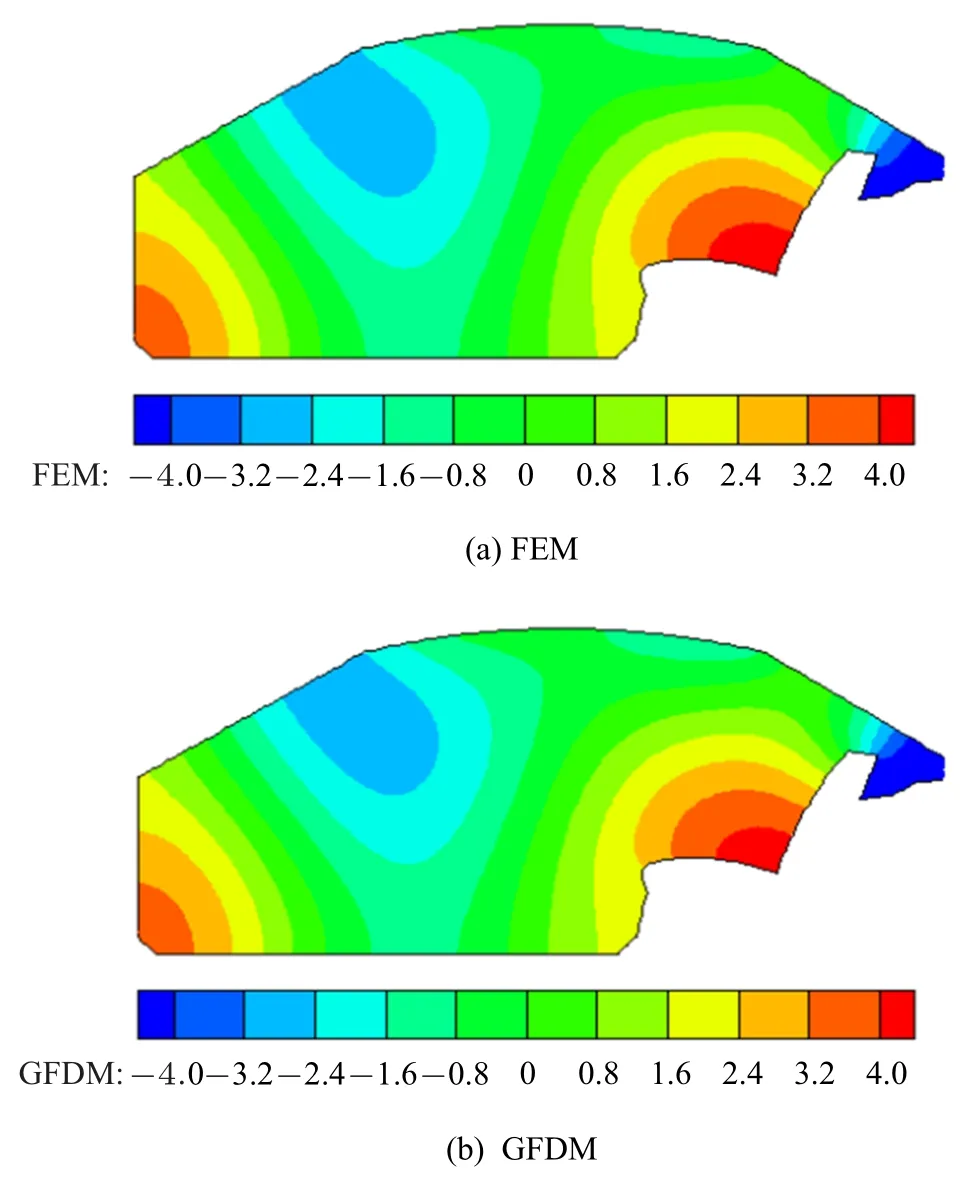
图8 有限元和广义有限差分法计算所得声压分布云图Fig.8 Contours of sound pressure obtained by the FEM and GFDM

为验证GFDM 在实际问题中的计算收敛性和稳定性,在GFDM 计算所用点数远小于FEM 离散节点的情况下,将三组不同的总节点数N计算所得数值结果与FEM 参考解对比分析,图9 和图10 分别给出了400 Hz 和600 Hz 频率下底部边界上的GFDM 和FEM 的对比情况.图9 展示了不同频率下的声压曲线,图10 是不同频率下的声压级曲线.

从图9 和图10 可以看出,GFDM 在不同节点数下计算所得声压和声压级均与有限元结果很大程度上吻合,即使采用较少的节点数目(N=11 558),GFDM 的计算结果也与有限元结果非常接近,表明算法是准确有效的.另外,从图9 和图10 中可以看出,GFDM 的计算精度随着计算节点数目的增加而提高,说明具有较好的收敛性.综上,GFDM 在求解含阻抗边界车腔声学问题时具有较好的计算稳定性和收敛性.相比于FEM,GFDM 无需网格划分等繁琐的前处理过程,仅需离散节点,所以可作为声腔分析的一种有效工具.

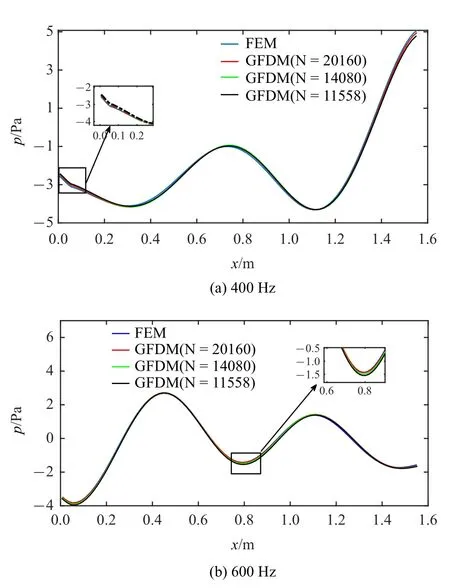
图9 频率为400 Hz 和600 Hz 时有限元法与广义有限差分法所得声压曲线的对比Fig.9 Comparisons of sound pressure obtained by the FEM and GFDM,under f=400 Hz and 600 Hz

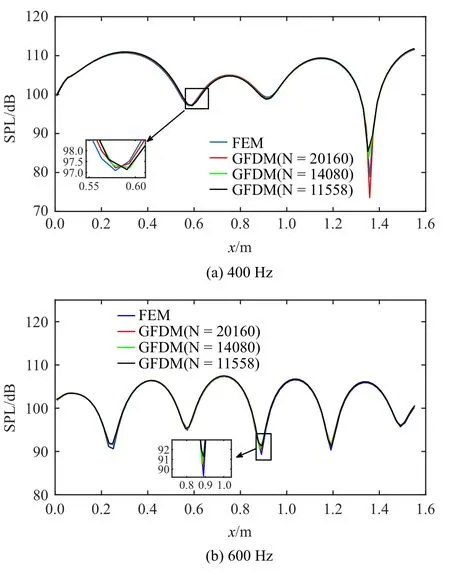
图10 频率为400 Hz 和600 Hz 时有限元法与广义有限差分法所得声压级曲线的对比Fig.10 Comparisons of sound pressure level obtained by the FEM and GFDM,under f=400 Hz and 600 Hz

3.3 三维空腔声场分析

为了检验GFDM 计算三维复杂声场问题的能力,下面对三维空腔模型的声学特性仿真计算[36],该声腔的介质为空气,模型的A 端面处带有初始速度条件,B 端面处是吸声材料,数值分析中所施加的Neumann 及Robin 边界条件也同上一算例一致.在有限元分析软件中,将声腔模型较细化划分为51 469 个单元,单元平均尺寸为0.011 m,将频率为400 Hz 下(根据声学“经验法则”,每波长内分布78 个网格单元)的有限元结果作为参考值.三维空腔结构的尺寸和布点方式如图11 所示.

图11 三维空腔及其GFDM 节点分布Fig.11 Three-dimensional cavity and the distribution of nodes

使用FEM 和GFDM 分别计算模型边界点上的声压,图12 和图13 分别给出了两种方法计算400 Hz时的声压和声压级分布云图.从图中发现,GFDM 计算的数值结果和FEM 参考值十分吻合,可见GFDM在三维声腔模型中也有较好的计算精度.

图12 400 Hz 下有限元和广义有限差分法所得声压分布云图Fig.12 Contours of sound pressure obtained by the FEM and GFDM under f=400 Hz

图13 400 Hz 下有限元和广义有限差分法所得声压级分布云图Fig.13 Contours of sound pressure level obtained by the FEM and GFDM under f=400 Hz

选取图11 中的F(0.05,0.05,0.12)点作为监测点来模拟人的耳朵所在位置,分析该处声压级随频率增加的变化情况.图14 给出了GFDM 和FEM 所得监测点F 处声压级频率响应曲线的对比.尽管在中频(700 Hz)附近和较高频率(>1000 Hz)附近出现了微小的偏差,但GFDM 的计算结果和FEM 参考解仍然比较吻合,充分表明了算法的有效性和准确性.需要指出的是,增加GFDM 的离散节点数目,可以使得两种算法的数值结果更加接近.

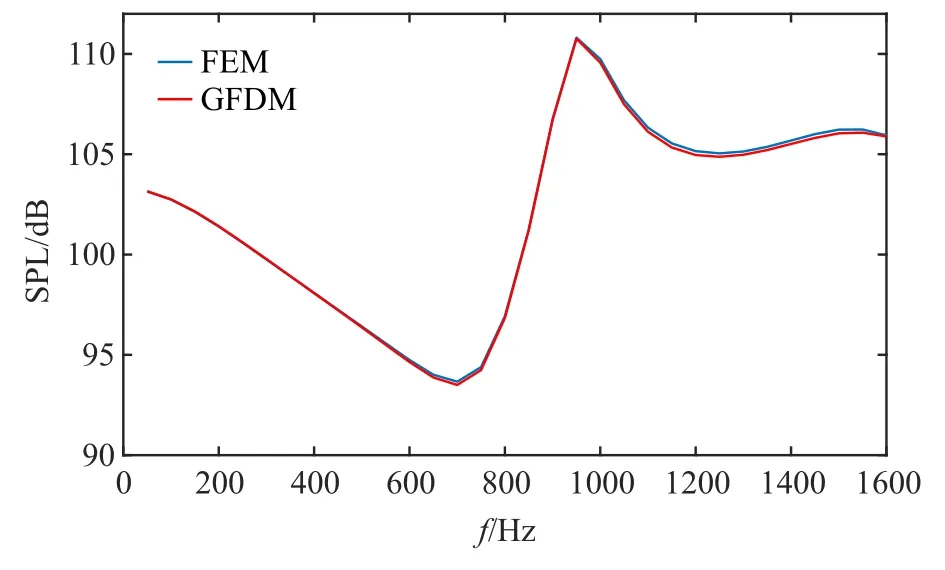
图14 监测点F 处的频率响应曲线Fig.14 Frequency response curves monitoring point F

3.4 三维S 型圆柱管道声场分析

圆柱管道是生活中比较常见的空腔模型,为了进一步验证本文方法的计算准确性,下面对S 型管道分别采用FEM 和GFDM 计算并对其声压分析.三维管道模型直径为D=0.1 m,长度L=1.0 m,a端面处施加Neumann 速度边界vn=0.01 m/s,b端面处有吸声材料,阻抗值Z=413 Pa·s/m3.其余边界条件为刚性壁,=0.模型尺寸和布点格式如图15 所示.

图15 S 型声腔及其节点分布Fig.15 S-shaped acoustic cavity and nodal distribution

为了保证GFDM 对高频问题的有效性,我们将模型离散成 126 905 个节点,此时的节点间距0.003 5 m.同时,将具有729 224 个网格单元(包含86 624 个边界单元和642 600 个域单元)和网格平均大小为0.003 m 的FEM 结果作为参考解.图16 和图17 分别给出了低频400 Hz 和高频1600 Hz 频率下管道表面声压分布云图以及绝对偏差云图.分析声压云图中可以发现,GFDM 计算的结果和FEM 参考解几乎完全吻合,并且从绝对偏差云图可以看出,400 Hz 下的偏差均小于0.06,1600 Hz 下的偏差均小于0.45,这充分说明了方法的可行性和有效性.因此,GFDM 在模拟含阻抗边界空腔问题时的计算精度和数值稳定性是比较理想的.

图16 400 Hz 下有限元和广义有限差分法所得声压和绝对偏差的分布云图Fig.16 Contours of sound pressure and absolute deviation obtained by the FEM and GFDM under f=400 Hz

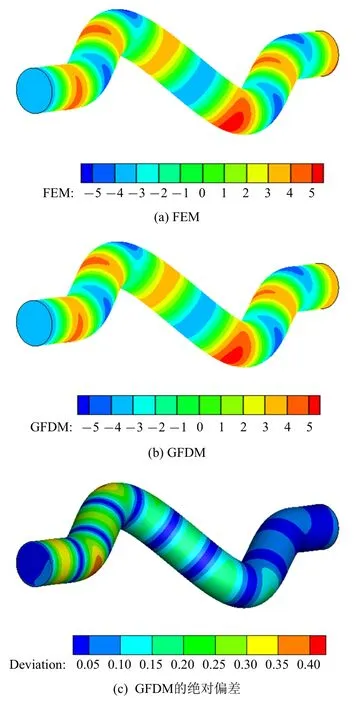
图17 1600 Hz 下有限元和广义有限差分法所得声压和绝对偏差分布云图Fig.17 Contours of sound pressure and absolute deviation obtained by the FEM and GFDM under f=1600 Hz

4 结论

广义有限差分法(GFDM)相比于传统网格类数值方法,避免了网格划分的前处理过程,并且继承了数值算法中局部化的优点,在模拟复杂高维几何域问题时有较好的准确性,并且保证计算精度的同时也提高了计算效率.本文探讨了GFDM 在含阻抗边界空腔声学问题中的应用.以具有精确解的二维管道边值问题为例,讨论了GFDM 的稳定性和计算高效性,并获得了最大计算频率与节点间距关系的经验公式.通过无精确解的复杂声腔模型声学分析,检验了GFDM 在二维和三维不同求解域内模拟计算的可行性、计算准确性和计算稳定性.

综上所述,广义有限差分法在空腔声学问题中的应用已得到初步验证,数值结果表明该方法是一种高效、精确、稳定、收敛的空腔声学分析方法.然而,应用广义有限差分法在更加实际的复杂声场中还需要进一步研究,进行声固耦合问题的求解和时域声学仿真将是未来工作的重点.