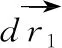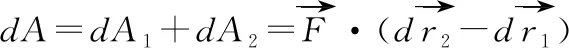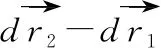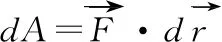探讨“一对内力功”的代数和

新疆

高中物理中所涉及的系统内力做功问题，例如弹力做功，摩擦力做功，磁场力做功，碰撞中的弹力做功等，在这些相互作用中，作用力与反作用力做功的代数和由什么决定？并且这个代数和与能量转化的关系是怎样的？本文从探讨高中物理中课堂教学的常见模型出发，探讨“一对内力功”代数和的问题。

力在空间的累积效果叫作功，而且力的作用是相互的，由两个或两个以上的质点组成的系统叫作质点组或者质点系，质点系以外的物体均称为外界，外界对质点系内质点的作用力称为外力，质点系内各质点间的相互作用力称为内力。然而内力功的问题在高中阶段是难点，例如两个质点A和B，内力的大小为FAB(A对B的力)和FBA(B对A的力)，FAB和FBA做的功分别为WAB和WBA，由于两质点A、B的运动情况不相同，WAB与WBA可能为零，可能都为正值，可能一正一负相加为零；也可能一正一负相加不为零。我们感兴趣的是这一对内力功的代数和什么时候为零，什么时候不为零，功又是能量转化的量度，当这个代数和不为零时，能量又是怎样转化的？

1.弹力功

1.1 斜劈滑块

如图1中，表面为弧形的光滑斜劈A放在一个光滑的水平面上静止，现在斜劈顶端处无初速度释放一个小物块B，在小物块下滑的过程中，A、B间弹力对斜劈做的功与对小物块做的功的代数和为多少？

图1

解：设重力对B做的功为WGB，弹力对A做的功为WA，弹力对B做的功为WB，对A、B组成的系统由动能定理有WA+WB+WGB=ΔEkA+ΔEkB①

ΔEkA和ΔEkB分别表示A、B两物体动能的增量。

由于A、B系统内仅有动能和重力势能相互转化，故系统机械能守恒-ΔEpB=ΔEkA+ΔEkB②

重力做功与重力势能变化的关系WGB=-ΔEpB③

联立①②③解得WA+WB=0 ④

可见，以上的解法由动能定理和机械能守恒定律联立得出内力功之和为零，并没有从正面直接解决问题，理由是机械能守恒的前提是系统外力不做功，系统内非保守力也不做功(这里的保守力仅限于重力和弹簧弹力)，支持力和压力是非保守力，既然认为机械能守恒，也就默认了非保守力不做功，即这一对弹力做功之和为零，也就没有证明的必要了。

1.2 绳子跨定滑轮

如图2，这是2014年海南的高考题，质量相同的两物体a、b间用不可伸长的轻绳跨接在一光滑的轻质定滑轮两侧，a在水平桌面的上方，b在水平粗糙桌面上，初始时用力压住b使a、b静止，撤去此压力后，a开始运动。在a下降过程中，b始终未离开桌面，在此过程中“D.绳的拉力对a做的功与对b做功的代数和为零”这是其中的一个选项。我们设ΔEa和ΔEb分别表示a，b机械能的增加量，Wf表示摩擦力对b做的功，Q表示产生的内能，对a、b系统用能量守恒定律有-ΔEa=ΔEb+Q①

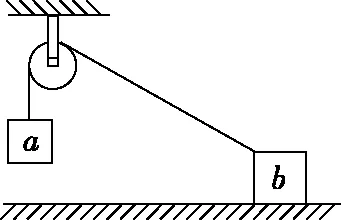
图2

由功能关系知Wa+Wb+Wf=ΔEa+ΔEb②

由功能关系知Wf=-Q③

联立①②③得Wa+Wb=0 ④

在这个问题中a、b系统的机械能是减小的，即机械能不守恒，我们依然得出了这一对内力功之和为零的结论。我们还可以推测在1.1中，若斜劈A与地面之间有滑动摩擦，可以断定，那一对弹力功之和依然为零，具体证明如下：设摩擦力对斜劈A做的功为Wf，产生的内能为Q，ΔEA和ΔEB分别表示A、B机械能的增加量，对A、B系统用功能关系，有WA+WB+Wf=ΔEA+ΔEB④

对A、B系统用能量守恒定律有-ΔEB=ΔEA+Q⑤

由功能关系知Wf=-Q⑥

联立④⑤⑥得WA+WB=0 ⑦

可见，一对内力功之和是否等于零和机械能守恒与否无关。

1.3 弹簧和两物体

如图3，弹簧对物体A的弹力与对物体B的弹力是一对内力，A、B两物体放在光滑的水平面，其间连一弹簧，现给物体A一个初速v0，从开始到弹簧长度最短时，弹力对物体A、物体B做的功分别为WA、WB，A、B动能的增加量分别为ΔEkA和ΔEkB，(ΔEkA<0)弹簧弹性势能的增加量为ΔEp，对A、B系统列动能定理WA+WB=ΔEkA+ΔEkB①

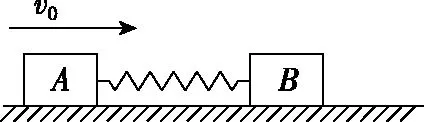
图3

对A、B系统列能量守恒定律-ΔEkA=ΔEkB+ΔEp②

联立①②得WA+WB=-ΔEp③

这说明：一对弹簧弹力做功的代数和等于其弹性势能的减少量。我们可以看到，物体A位移大于物体B位移，故|WA|>WB，即WA+WB<0，将③式改成-(WA+WB)=ΔEp，可以看出，克服一对弹簧弹力做的功等于系统弹性势能的增加量。

反思：这里的WA+WB为什么不等于零呢？很显然是由于A、B两物体的位移不一样大，导致弹簧长度发生了变化，即动能转化为弹性势能。

2.摩擦力功

2.1 滑块木板

如图4，木板B在光滑的水平面匀速向右运动，这时，无初速度释放一物块A，最终二者一起匀速运动(物块A没有从木板B上掉下)，若在这个过程中，摩擦力对物块A做的功为WfA，对木板B做的功为WfB，因摩擦产生的内能为Q，用ΔEkA和ΔEkB分别表示A、B动能的增加量，在没有计算之前，有读者会认为|WfB|=Q，认为木板B克服摩擦力做的功等于产生的内能。但是，木板B克服摩擦力做的功等于其动能的减少，如果全部等于产生的内能，那么物块A的动能增大又怎么解释呢？

图4

对系统A、B列动能定理WfA+WfB=ΔEkA+ΔEkB①

对系统A、B列能量守恒-ΔEkB=ΔEkA+Q②

联立①②得-(WfA+WfB)=Q③

这说明：克服一对滑动摩擦力做功之和等于内能的增加量(也就是我们平时所说的Q=fs相对)

反思：这里的WfA+WfB为什么不等于零呢？很显然，物块A与木板B的位移不一样大，导致物块A在木板B上滑动，从而产生了内能。

在电磁感应现象中，对于动生电动势的能量转换，我们常说“克服安培力做的功等于产生的电能”。但是，这句话是不完整的，例如在电磁驱动中，安培力是物体运动的动力，不存在“克服”这一说法，何况，这时安培力做了功，使物体具有动能，而不是电路中的电能，关于这个问题，是否也涉及到内力功的问题呢？

3.磁场力功

3.1 电磁驱动1

如图5，光滑平行金属导轨固定在水平面上，左端由导线相连，导体棒垂直静置于导轨上构成回路。在外力F作用下，回路上方的条形磁铁竖直向上做匀速运动。在匀速运动过程中外力F做功WF，磁场力对导体棒做功W1，磁铁克服磁场力做功W2，重力对磁铁做功WG，回路中产生的焦耳热为Q，导体棒获得的动能为Ek。则

( )

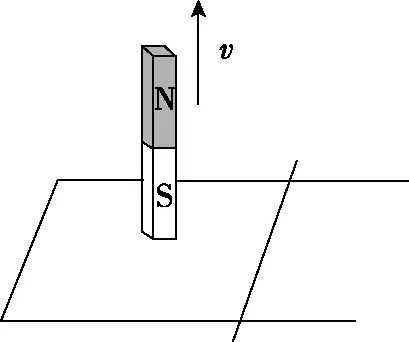
图5

A.W1=QB.W2-W1=Q

C.W1=EkD.WF+WG=Ek+Q

对导体棒列动能定理，可知C项正确，对磁铁和导体棒组成的系统列动能定理WF+W1-W2+WG=Ek①

对系统列能量守恒WF=Ek+ΔEp+Q②

由功能关系WG=-ΔEp③

联立②③，可知D正确，再由D项和①联立，可知B正确。

B项是什么意思呢？如果我们将它写成

-(-W2+W1)=Q④

其中-W2为磁场力对磁铁做的功，W1为磁场力对导体棒做的功，-W2+W1为这一对磁场力做功之和，这个和为负值，这也是显而易见的，括号前面的负号表示“克服”。因此，我们可以说“克服一对磁场力做功之和等于电能”，然而，造成这一对内力做功之和不为零的原因是磁铁与导体棒发生了相对运动，导致机械能转化为电能。下面我们继续讨论电磁驱动中内力功的问题。

3.2 电磁驱动2

如图6，是一个磁悬浮列车的原理简化图，纸面为轨道平面，垂直纸面向里和向外的磁场相互间隔，每个磁场的长和宽分别为s和l，矩形线框abcd(与磁场的长，宽相同)固定在车厢底板，当磁场以速度v0向右匀速运动时，线框也跟着向右运动，当线框的速度为v时(v

图6

线框产生的感应电动势为E=2Bl(v0-v)①

将①两边同乘以电流I，得EI=2IBl(v0-v)②

安培力F=2IlB③

而电功率P电=EI④

联立②③④可得P电=Fv0-Fv⑤

将⑤变形为-(-Fv0+Fv)=P电⑥

其中，-Fv0表示安培力对磁场做功的功率，Fv表示安培力对线框做功的功率，-Fv0+Fv表示一对安培力功率之和，-(-Fv0+Fv)表示克服这一对安培力功率之和，故⑤的含义是克服这一对安培力功率之和等于电功率，如果两边同乘以时间t，我们就可以说克服这一对安培力做功之和等于产生的电能。然而，造成这一对内力功之和不为零的原因是线框与磁场之间发生了相对运动，产生了电能，这一对安培力做功之和为负值是必然结果。

4.理论证明

(a)

(b)

这一对内力元功的代数和为

表明两质点间相互作用力的元功的代数和等于力与相对元位移的标积。

表明一对作用力和反作用力做功的代数和取决于力和质点间的相对位移，即一对内力功的代数和等于力乘在力的方向上的相对位移，功的正负由力的正负和力的方向上位移的正负决定，可以得出，两质点在力的方向上没有发生相对运动时，内力功的代数和为零，这句话是判断一对内力功之和是否等于零的依据。到这里我们不禁想起碰撞问题，在一维非弹性碰撞中，两物体在力的方向上有相对运动(物体发生了形变)，内力功之和不为零而是一个负值，故系统机械能不守恒，而这个和的绝对值为系统损失机械能的值，在弹性碰撞中，物体碰撞后恢复了原状，两物体在力的方向上没有发生相对运动，内力功之和为零，机械能无损失，故守恒。现在，也很容易解释了为什么完全非弹性碰撞损失的机械能最多的问题。