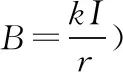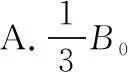多条通电直导线周围磁场叠加问题的进阶学习
2021-05-29安徽
安徽
多条通电直导线周围磁场叠加问题中的通电直导线可能处于平行且共面状态,也可能处于相互交叉且共面状态。既不平行也不共面的状态在高中阶段基本不涉及,本文暂不探究。解决此类问题常用到安培定则和平行四边形定则等知识,下面通过几道高考题和经典习题加以探究。
一、两条通电直导线周围磁场的叠加问题
1.两条相互平行的通电直导线周围磁场的叠加
1.1 两条通有反向电流的直导线周围的磁场叠加
【例1】(2012·全国卷)如图1,两根互相平行的长直导线过纸面上的M、N两点,且与纸面垂直,导线中通有大小相等、方向相反的电流。a、O、b在M、N的连线上,O为MN的中点,c、d位于MN的中垂线上,且a、b、c、d到O点的距离均相等。关于以上几点处的磁场,下列说法正确的是
( )
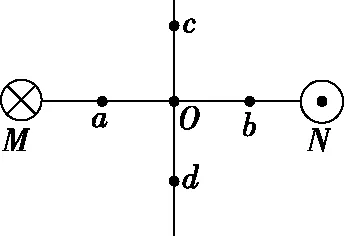
图1
A.O点处的磁感应强度为零
B.a、b两点处的磁感应强度大小相等,方向相反
C.c、d两点处的磁感应强度大小相等,方向相同
D.a、c两点处磁感应强度的方向不同
【解析】由安培定则可知,两电流在O点处的磁场方向都向下,O点处的磁感应强度不为零,A错误;a、b两点处的磁感应强度大小相等,方向相同,B错误;c、d两点处的磁感应强度大小相等,方向相同,C正确;a、c两点处的磁感应强度方向相同,都向下,D错误。
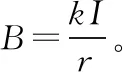
【例2】(2011·全国卷)如图2,两根相互平行的长直导线分别通有方向相反的电流I1和I2,且I1>I2;a、b、c、d为导线某一横截面所在平面内的四点,且a、b、c与两导线共面;b点在两导线之间,b、d的连线与导线所在平面垂直。磁感应强度可能为零的点是
( )
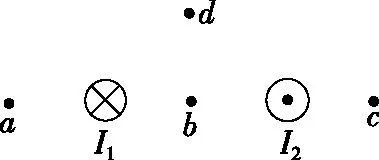
图2
A.a点 B.b点 C.c点 D.d点
【解析】根据安培定则可知I1和I2电流在a处产生的磁场方向分别为垂直ac连线向上和向下,由于I1>I2,且I1电流与a点的距离比I2电流与a点距离要小,故B1a>B2a,则a点磁感应强度不可能为零,A错误;两电流在b处产生的磁场方向均垂直ac连线向下,则b点磁感应强度不可能为零,B错误;I1和I2电流分别在c处产生的磁场方向为垂直ac连线向下和向上,且I1电流与c点的距离比I2电流与c点距离要大,故B1c与B2c有可能等大反向,则c点磁感应强度可能为零,C正确;两电流在d处产生的磁场方向一定成某一夹角,且夹角一定不为180°,则d点磁感应强度不可能为零,D错误。
【点评】例2与例1相比,两导线中的电流由等大反向变为不等大反向,欲使平面内某点磁感应强度为零,则该点一定在小电流的外侧,即c点。若再将两根导线相互平行地自由置于光滑的水平面上,只要在c点所在直线平行放置电流大小合适且与I1同向的导线,即可让三根导线处于平衡状态。
1.2 两条通有同向电流的直导线周围磁场的叠加
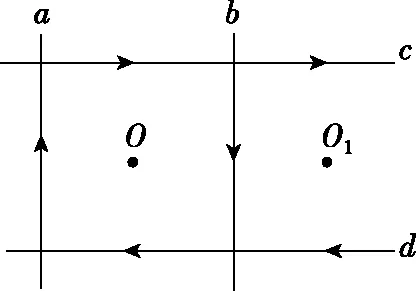
【例3】(2017·全国卷Ⅲ)如图3,在磁感应强度大小为B0的匀强磁场中,两长直导线P和Q垂直于纸面固定放置,两者之间的距离为l。在两导线中均通有方向垂直于纸面向里的电流I时,纸面内与两导线距离为l的a点处的磁感应强度为零。如果让P中的电流反向、其他条件不变,则a点处磁感应强度的大小为
( )

图3
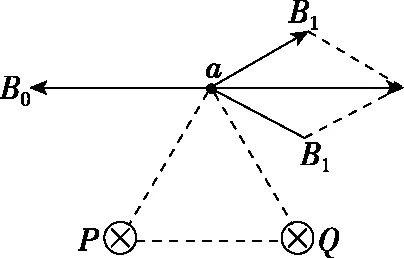
图4
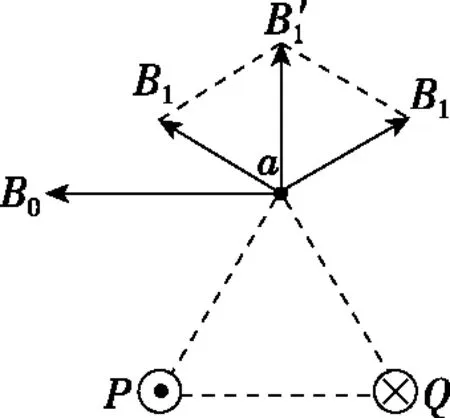
图5
【点评】本题考查两根相互平行通电直导线间的磁场叠加问题,涉及矢量合成法则的运用。用叠加原理计算磁感应强度的基本思路是:(1)确定需要计算磁感应强度的位置和周围的场源。(2)利用安培定则和常见磁体周围磁场分布特点,分别确定各场源在该位置的磁感应强度大小和方向。(3)根据平行四边形定则,采用合成和正交分解的方法求出磁感应强度的矢量和,即为该位置的磁感应强度。
2.两条相互垂直的通电直导线周围磁场的叠加
( )

图6
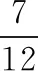


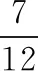
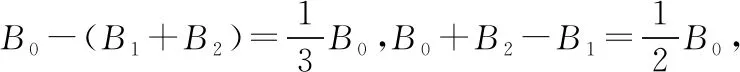
【点评】a、b两点的磁场除了两条互相垂直的通电直导线产生的磁场,还有外加磁场B0,即合磁场涉及三个磁场的叠加。先利用安培定则判断出通电直导线各自产生的磁感应强度,然后利用矢量叠加原理即可求出各点产生的磁感应强度。
二、三条通电直导线周围磁场的叠加问题
1.三条相互平行的通电直导线周围磁场的叠加
【例5】(2017·全国卷改编)如图7,三根相互平行的固定长直导线L1、L2和L3两两等距,均通有大小均为I的电流,L1中电流方向与L2中的相同,与L3中的相反,下列说法正确的是
( )
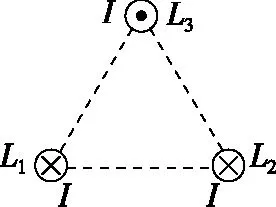
图7
A.L1、L2在L3处产生的合磁场方向与L1、L2的连线垂直
B.L2、L3在L1处产生的合磁场方向与L2、L3的连线垂直
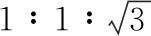
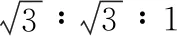

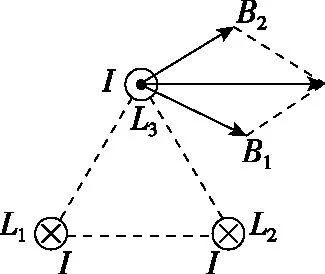
图8
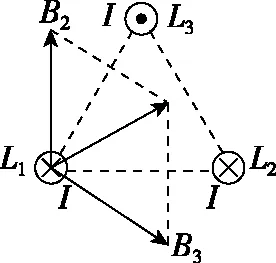
图9
【点评】本题考查安培定则、左手定则和磁场的叠加。AB两个选项的求解可以参考例3;CD两个选项可以结合“同向电流相互吸引,反向电流相互排斥”快速判断。另外本题还可以继续涉及等边三角形中心处的磁场进行命题。
2.三条互成角度的通电直导线周围磁场的叠加
【例6】(2013·海南卷)三条在同一平面(纸面)内的长直绝缘导线组成一等边三角形,在导线中通过的电流均为I,方向如图10所示。a、b和c三点分别位于三角形的三个顶角的平分线上,且到相应顶点的距离相等。将a、b和c处的磁感应强度大小分别记为B1、B2和B3,下列说法正确的是
( )
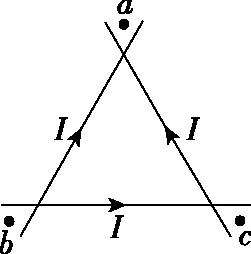
图10
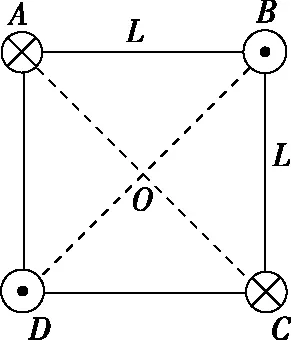
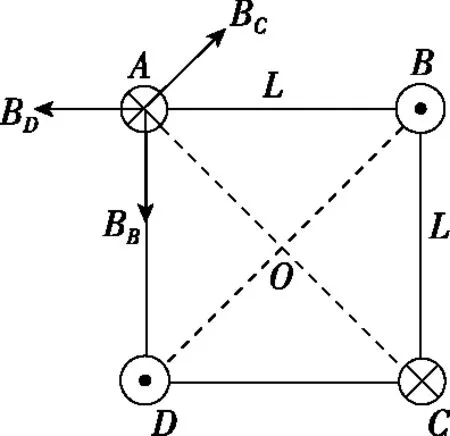
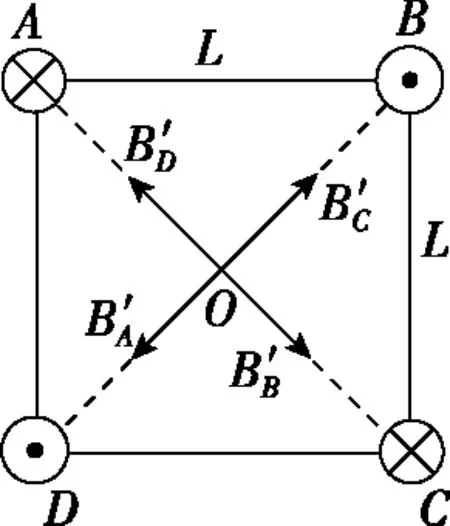
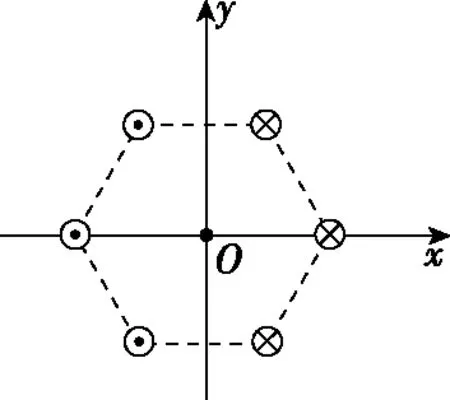
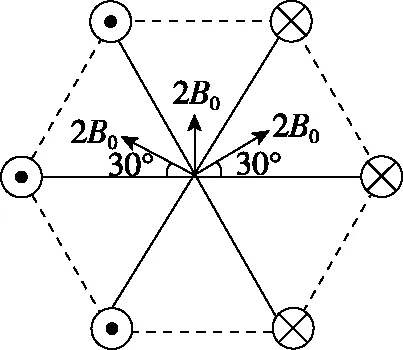
A.B1=B2 B.B1=B2=B3 C.a和b处磁场方向垂直于纸面向外,c处磁场方向垂直于纸面向里 D.a处磁场方向垂直于纸面向外,b和c处磁场方向垂直于纸面向里 【解析】由于通过三条导线的电流大小相等,结合安培定则及矢量叠加法则可判断出,三条导线在a、b处产生的合磁感应强度垂直纸面向外,在c处垂直纸面向里,且B1=B2 【点评】本题考查安培定则和磁场的叠加。通电导线周围存在磁场,且离导线越远磁感应强度越弱;磁场不但有大小而且有方向,方向相同则相加,方向相反则相减。 ( ) 图11 A.电流的大小为I1=2I2 B.四根导线所受的磁场力都为零 C.正方形中心O处的磁感应强度为零 D.若移走A导线,则中心O处的磁场将沿OB方向 图12 图13 【例8】如图14所示为六根与水平面垂直的导线的横截面示意图,导线分布在正六边形的六个顶点,导线所通电流方向已在图中标出。已知每根导线在O点处产生的磁感应强度大小为B0,则关于正六边形中心O点处的磁感应强度大小和方向的说法正确的是 ( ) 图14 A.大小为零 B.大小为2B0,方向沿x轴负方向 C.大小为4B0,方向沿x轴正方向 D.大小为4B0,方向沿y轴正方向 【解析】根据右手定则,每根通电导线在中心O点处产生磁场的磁感应强度的方向如图15所示,由平行四边形定则可知B=2B0+2×2B0cos60°=4B0,方向沿y轴正方向,D正确,ABC错误。 图15 【点评】例7和例8均涉及安培定则和磁场叠加原理,解题思路与例1、例2、例3和例5类似,正确地利用安培定则和平行四边形定则可以快速解题。 ( ) 图16 【点评】本题考查学生的推理能力,需要应用磁感应强度矢量叠加原理和安培定则解题。三、三条以上通电直导线周围磁场的叠加问题
1.三条以上相互平行的通电直导线周围磁场的叠加

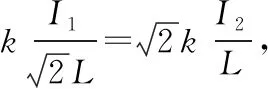
2.三条以上互成角度的通电直导线周围磁场的叠加