输电线路圆形截面基础偏心受拉配筋计算方法

(中国电力工程顾问集团西南电力设计院有限公司，四川 成都 610056)

0 引言

输电线路中常用的钢筋混凝土基础形式包括掏挖基础、挖孔桩基础和岩石基础等，其主柱截面通常为圆形，由于风荷载和角度力的存在，基础往往会受到上拔荷载，同时存在水平荷载，此时基础的受力状态为偏心受拉。

大多构筑物的基础只承受压力，表现为偏心受压，文献[1-4]针对钢筋混凝土圆形截面偏心受压构件的配筋计算方法进行了探讨。而针对钢筋混凝土圆形截面偏心受拉构件配筋计算方法的研究很少，文献[5]按原型基本公式求解配筋时，未知量α(对应于受压区混凝土截面面积的圆心角(rad)与2π的比值)步长极小，可以理解为试算法，计算效率较低。

DLT 5219—2014《架空输电线路基础设计技术规程》[6]条文7.1.3给出了钢筋混凝土圆形截面偏心受拉构件纵向钢筋截面面积的计算方法，当偏心距e0不大于计算截面中心至纵向钢筋截面中心距离的1/2时，可以按照简化公式计算；否则需要求解超越方程，其计算方法与矩形截面存在巨大差异，不能采用通常的直接解法进行计算，只能依赖于数值算法。文献[7]中给出了图表查系数法，该图表即为混凝土结构计算手册中采用的图表，该方法计算配筋存在一定的误差，且不便于工程应用。

本文从钢筋混凝土圆形截面偏心受拉构件正截面承载力计算方程组出发，对配筋计算公式进行了整理，提出了高效的钢筋面积数值计算方法，并且证明了该方法求解的可靠性和唯一性。

1 基本公式

根据GB 50010-2010《混凝土结构设计规范》[7]附录E.0.5，可以得到沿周边均匀配置纵向钢筋的圆形截面偏心受拉构件的正截面受拉承载力计算式：

式中：N为构件的轴心拉力设计值；Nu0为构件的轴心受拉承载力设计值；e0为轴向拉力作用点至截面重心的距离；Mu为构件的正截面受弯承载力设计值；A为圆形截面面积；fy为纵向普通钢筋的强度设计值；fc为混凝土抗压强度设计值；As为全部纵向普通钢筋的截面面积；r为圆形截面的半径；rs为纵向普通钢筋重心所在圆周的半径；α为对应于受压区混凝土截面面积的圆心角(rad)与2π的比值；αt为纵向受拉普通钢筋截面面积与全部纵向普通钢筋截面面积的比值，当α＞0.625时，αt为0；α1为系数，输电线路中基础混凝土强度等级不超过C50，α1取1.0。

在偏心受拉作用下，圆形截面受力简图如图1所示，其中阴影区为受压区。

图1 圆形截面受力简图

由式(1)～式(5)可知，方程组的未知量为As和α，为了得到钢筋面积，需要求解超越方程组，可采用迭代法求数值解。

2 计算过程

将公式(1)取等号可得：

式(7)的表达式比较复杂，收敛性证明困难，因此可以从式(4)出发，假定一个初始钢筋截面面积As0，通过数值迭代的方法求解出对应的α，然后将α代入到式(7)即可求解出一个新的钢筋截面面积As1，再将As0与As1进行比较，如果|As0-As1|达到要求的精度即可终止计算，否则将(As0+As1)/2作为初始值，重复以上计算过程，直至达到要求的计算精度，钢筋计算面积取最后一步As0和As1的较大值即可。

将α代入到式(7)后，式(7)即为关于As的一元二次方程，计算比较容易，假定B=(l1l2fy-l3Nfy-Ne0fy)，C=-Nl1l2，求解As1的公式为：

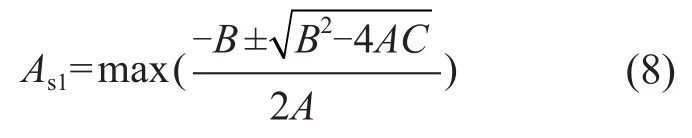
为了提高计算效率，初始As0可根据构造要求取最小配筋面积Asmin，代入式(4)通过迭代法可求解出对应的α，如果式(1)成立，则计算过程结束，不再进行迭代计算，钢筋面积为最小配筋率控制，有效的规避了配筋计算面积较小甚至为负的情况。配筋计算过程如图2所示。

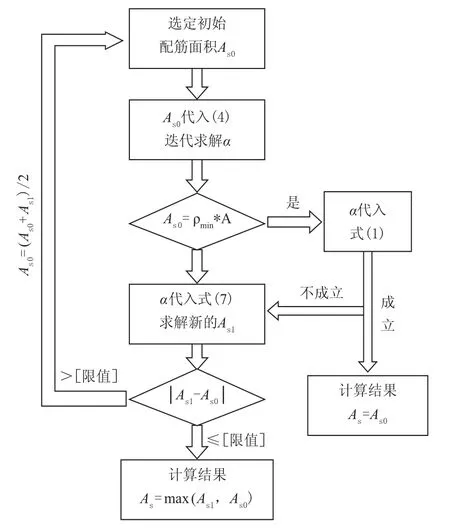
图2 配筋计算过程

3 迭代方法

计算过程中的关键在于当给定一个初始截面面积As0时，如何快速地计算出对应的α，式(4)为非线性方程，不能直接计算，需要采用数值迭代的方法求解出对应的α。

非线性方程常用的求根方法包括二分法、牛顿法等。二分法通过不断地把函数的零点所在的区间一分为二，使区间的两个端点逐步逼近零点，进而得到零点近似值，具有线性收敛速度。牛顿法是一种线性化方法，具有二阶收敛速度，本文采用收敛速度更快的牛顿法。对于偏心受拉圆形截面，其受压区面积所占的比例一般不会太大，在迭代求解α时其初始值可取0.3。牛顿法近似解的表达式为：

如果函数f(α)在求解区间(m,n)上连续、严格单调，且f(m)f(n)＜0，这时函数在区间(m,n)内有且仅有一个实根，满足牛顿法的应用条件。

4 算法收敛性证明

从单调性和唯一性出发，对算法收敛性进行证明。

4.1 单调性证明

为了证明公式(4)的收敛性，将其构造为以下函数：

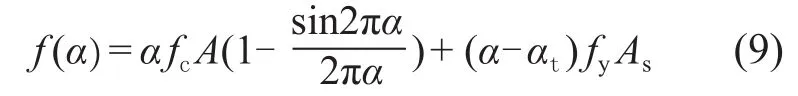
由GB 50010—2010《混凝土结构设计规范》附录E.0.4可知：

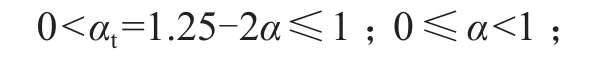
因此可以得到α的取值区间为0.125≤α＜1，当α＞0.625 时αt等于 0。

将式(9)改写为关于α的分段函数：

当0.125≤α≤0.625时：

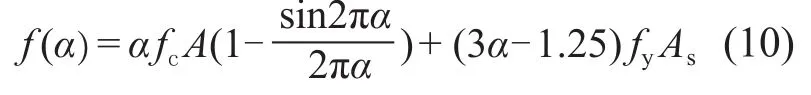
当 0.625＜α＜1 时 ：

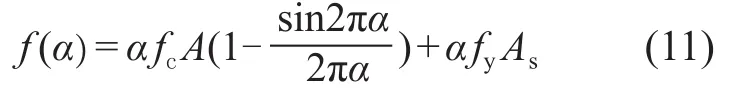
容易看出函数f(α)在0.625点保持连续，符合牛顿法的基本要求。其一阶导数计算如下：

当0.125≤α≤0.625时：

当 0.625＜α＜1时 ：

由式(12)和式(13)容易得出，一阶导数f'(α)在整个区间内存在，且均大于0，因此f(α)是严格单调递增的函数。一阶导数f'(α)在0.625点并不连续，说明f(α)在0.625处不光滑，但并不影响此函数的收敛性，当取到0.625这个点时，取左端或者右端的导数均能收敛到真解，左端的一阶导数更大，可优先取左端的导数，收敛速度更快。

当采用牛顿法迭代求解α时，近似根的表达式为：

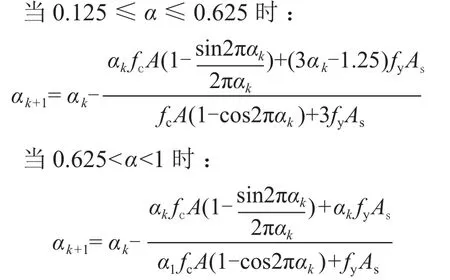
4.2 唯一性证明

为了证明函数f(α)在区间内具有唯一的实数解，可计算区间的两个端点值：

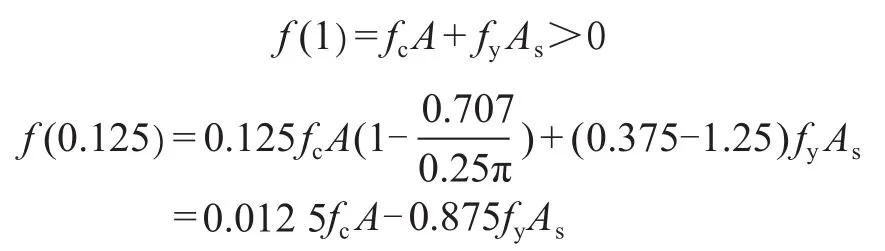
架空输电线路中常用的基础混凝土等级为C25和C30，纵向普通钢筋等级为HRB400，根据JGJ94—2008《建筑桩基技术规范》条文4.1.1可知，正截面配筋率可取0.65%～0.2%。为了计算出f(0.125)的最大值，混凝土等级取为C30，最小配筋率取为0.2%，可得：

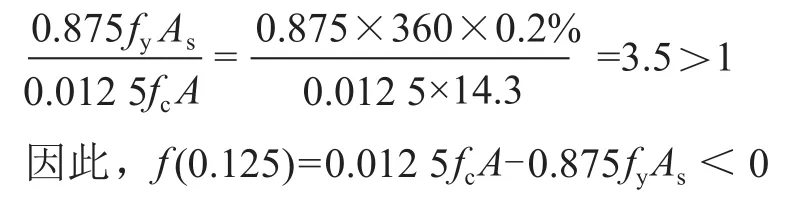
以上过程证明了函数f(α)在区间[0.125, 1)内连续、严格单调递增、有且仅有一个实根，因此给定一个初始钢筋截面面积以后，可以采用牛顿法求解出式(4)中对应的α。

5 算例

通过两个算例来验证本文配筋计算方法的准确性和收敛性，算例一的配筋为最小配筋率控制，算例二的配筋为计算控制。

算例计算对象为承受偏心受拉的圆形截面基础，基础桩径d=1 400 mm，混凝土强度等级为C30，纵向钢筋等级为HRB400，纵向钢筋保护层厚度为60 mm，最小配筋率为0.5%，算例均由西南电力设计院有限公司自主开发的单桩批量快速计算软件完成。

5.1 算例一

假定轴向拉力N=1 000 kN，偏心距e0=1 000 mm。按照前述计算过程，首先求解出满足构造要求的最小配筋面积Asmin=7 693 mm2，再通过牛顿法求解出式(4)中对应的α，迭代时初始α可取0.3，迭代过程如表1所示：

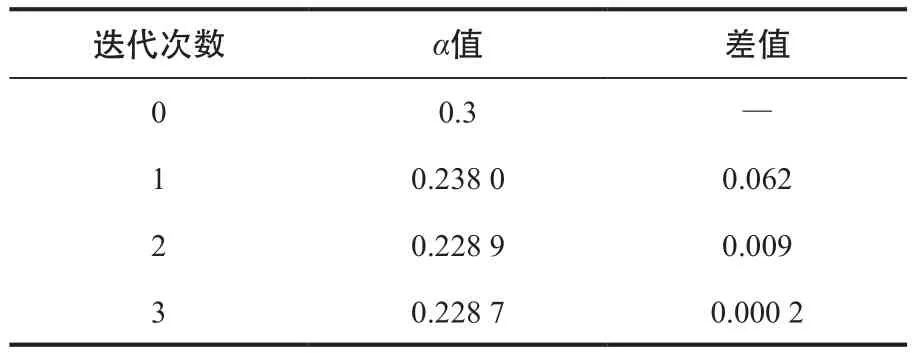
表1 算例一迭代过程

由以上迭代过程可知，当迭代3次时α就达到了较高的精度，将α代入到式(1)可以得到：

因此，式(1)成立，说明此时钢筋面积由最小配筋率控制，不再进行计算。

5.2 算例二

假定轴向拉力N=2 000 kN，偏心距e0=1 000 mm。由于N＞1 027 kN，所以公式(1)不成立，钢筋面积为计算控制，将算例一求出的初始Asmin对应的α代入式(8)即可求出新的钢筋面积As1，如此往复计算直至钢筋面积达到规定的精度，迭代过程如表2所示。

表2 算例二迭代过程

由以上迭代过程可知，当迭代15次时配筋面积已基本收敛，As1与As0的差异在0.5%，计算精度在工程可接受的范围内，最终的钢筋计算面积为15 623 mm2。将最后一个迭代步的α和As1代回到原方程组，计算表明结果吻合，证明了本文计算方法的准确性和可靠性。

6 结语

本文针对输电线路中常用的圆形截面基础，提出了基础偏心受拉时纵向普通钢筋截面面积的计算方法，并且证明了该计算方法的收敛性和可靠性。算例表明，该方法计算效率高、准确性好，目前已在西南电力设计院有限公司自主开发的单桩批量快速计算软件中得到应用。