高压条件下椭圆孔喷雾破碎雾化分析

陆大勇,贾和坤，叶 泽

(江苏大学 汽车与交通工程学院，江苏 镇江 212013)

随着汽车尾气带来的环境污染问题受到广泛关注，人们对车用发动机燃烧过程的优化研究便从未停止[1-2].对于柴油机来说，高压共轨喷射系统因能够提供更好的雾化质量与燃烧效果而被广泛采用.在高压共轨喷射系统中，提高燃料与空气的混合质量对整个发动机燃烧做功过程具有重要意义[3-5].其中初次破碎是喷雾发展历程的始点，对燃油二次雾化质量具有重要影响，引起了中外学者的广泛关注.

文献[6]运用X射线技术研究了近场喷雾的速度与湍流强度，发现近场喷雾轴向速度的衰减率比径向低，喷射压力对近场的速度和湍流强度影响较大.喷孔形状能够影响初始破碎的不稳定性，文献[7]证明了使用非圆形孔能提高雾化质量.文献[8]研究了90 MPa下的椭圆孔喷嘴喷射特性，结果表明，在高喷射压力下椭圆孔也会出现换轴现象.文献[9]对环境压力下的非圆形喷孔和圆形喷孔进行了宏观喷雾对比试验，发现换轴现象有助于改善喷雾特性.文献[10]进行了椭圆孔和圆孔的射流试验，发现椭圆孔的射流分裂长度比圆孔短.文献[11]通过对不同几何孔喷嘴的混合特性的计算分析，得出了椭圆孔射流比等效面积的圆形孔和矩形孔射流表现出更高的速度衰减率和射流扩散速率的结论.文献[12]比较了在相同的喷射条件下不同横纵比的椭圆孔和圆形孔口的喷雾特性，发现椭圆孔的喷雾混合质量均优于圆形孔，且纵横比4和6的椭圆孔喷雾比纵横比2的混合质量更高.

以上研究虽然对初次破碎和异形喷孔进行了一定的研究，但是对高喷射压力条件下的椭圆孔初次破碎，尤其在喷孔形状对初次破碎的影响以及初次破碎对喷雾发展过程的影响方面研究较少.所以文中采用LES与VOF相耦合的方法，研究椭圆喷孔初次破碎特性与换轴现象，并结合不同高喷射压力下椭圆孔喷雾发展过程的试验数据分析椭圆孔喷雾初次破碎对雾化现象的影响.

1 数值模拟

1.1 数值模型

大涡模拟的连续性方程和动量方程如下：

(1)

(2)

文中采用Smagorinsky-Lilly模型作为子网格尺寸模型，其中SGS应力公式如下：

(3)

(4)

式中：μt是亚格子湍流黏度.

(5)

(6)

子网格的混合长度Ls为

Ls=min(kd,CsΔ)，

(7)

式中：k表示von Kármán常数；d表示距离壁面的最近距离；Cs表示Smagorinsky常数；Δ表示网格的尺寸.在计算流体学中，网格的尺寸Δ是根据单元的体积计算得到的，计算公式如下：

Δ=(ΔxΔyΔz)1/3，

(8)

文献[13]发现Smagorinsky常数为0.23 适用于惯性范围内的各向同性湍流，而Cs值为0.10时适用于各种流体，产生的模拟效果最佳.

在建立耦合孔内流动的初次雾化模型时，考虑到喷孔内部空化与湍流对初次射流的强化作用，采用VOF模型，可以通过求解一组动量方程并追踪不同的相位分数来实现对多种流体的模拟，而模拟计算主相的体积分数会根据约束条件进行求解，确保主相体积分数的准确性.动量方程的表达式如下：

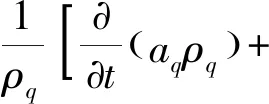
(9)

式中：′mqp代表质量从相位q传递相位p，而′mpq则相反，表示质量从相位p传递到相位q.

1.2 网格剖分

考虑到模拟的边界层和喷雾的雾化区域，选择六面体结构网格进行模拟计算，如图1所示.由于椭圆孔的雾化结构不是轴对称的，所以雾化区域也进行了网格化处理.分别选择压力条件和平均压力条件作为进口边界和出口边界，速度无滑移条件用于管壁边界.

图1 网格和计算域信息

文中采用了网格密度区域化来解决喷嘴内部流动敏感区域不同的问题.同时用不同的网格尺寸来提高网格分辨率，进而提高模拟结果的准确性.图2给出了喷射压力120 MPa，背压3 MPa条件下，不同网格尺寸对圆形孔质量流量的影响.图中可以发现，网格尺寸为2 μm左右时，质量流量基本稳定在6.57 g·s-1.考虑计算时间和计算精度，喷孔部位采用2 μm的网格，雾化室内采用5 μm的网格，网格总数为480万个，满足数值模拟的精度.

图2 喷射压力120 MPa、背压3 MPa时椭圆喷孔质量流量

1.3 模型验证

图3展示了喷射压力为120 MPa，背压为3 MPa条件下，圆孔(孔径为0.25 mm)喷雾的模拟与试验结果.

图3 近场喷雾模拟与试验结果对比

由图3a可以发现，试验与模拟的结果接近，喷雾尖端形状都为蘑菇状.但是试验与模拟结果还存在一定的差异，从试验结果可以看出，近场喷雾的尖端存在大量细小液滴，在模拟结果中无法体现.其原因是计算模拟中，网格的数量不足以模拟气相的小涡流，而小涡流会影响液滴的破碎和雾化.图3b将试验与模拟的喷雾穿透速度进行了对比，可以发现两个结果吻合较好，最大的速度偏差在3.4 μs时刻，偏差为3.5%.通过以上对比分析可以发现，基于LES和VOF相耦合的喷雾模型准确性较高，可以较为准确地分析喷雾的初次破碎过程.

1.4 模拟边界条件

椭圆孔的结构参数如下：长轴237.3 μm；短轴107.9 μm；喷嘴出流面积20 106.2 μm2；湿润周界597.8 μm；孔长1.23 mm；长径比2.2.

在大涡模拟计算中采用了长径比为2.2的椭圆孔进行模拟计算.边界条件如下：喷射压力为120,140和160 MPa；背压3 MPa；平均温度300 K；柴油密度830 kg·m-3；动力黏度2.57 mm2·s-1；表面张力0.028 N·s-1；十六烷值48.

2 试验方法

2.1 试验台架

采用Mie散射法获取的喷雾宏观图像，光源由YAG激光器提供，激光波长为532 nm.在CCD相机上安装532 nm的滤光片，相机垂直于激光器布置.由于滤光片只允许532 nm波长的光线进入，故能够精确获取喷雾的散射图像.喷射压力由高压共轨系统控制，可实现50～180 MPa范围内精准的喷射压力调节.喷射系统如图4所示.

图4 试验装置图

2.2 试验条件

图5给出了单孔喷嘴的结构，喷孔形状采用了大长径比的椭圆喷孔和直径为160 μm的圆形喷孔，为保证试验的对比性，椭圆形喷孔的面积与圆形喷孔保持相同.为了确保加工精度在±0.1 μm以内，采用激光微钻孔进行加工.试验时的边界条件如下：喷射压力为120、140和160 MPa；背压3 MPa；平均温度300 K.

图5 圆孔与椭圆孔的几何形状及尺寸

3 结果分析

3.1 数值结果分析

文中采用文献[14]定义的喷雾速度半值宽来判定椭圆形喷孔在喷射过程中是否存在换轴现象.当径向方向速度是射流中心速度一半的位置，这个位置与射流中心的距离就是速度半值宽.

图6展示了不同高喷射压力条件下，椭圆孔主次平面上喷雾速度半值宽.由图可以观察到，主次平面上的喷雾速度半值宽初始时随着时间增加，但其大小不同，主平面的喷雾速度半值宽在初始时间内大于次平面.但随着时间的推移，次平面喷雾速度半值宽超过主平面，两者喷雾速度半值宽相互交替直至达到相近的水平.其中在喷射压力为120 MPa时，换轴现象仅出现1次，而在喷射压力为160 MPa时，换轴现象出现4次，远高于120 MPa下的换轴次数.由此可得到与文献[8]相同的结论，即在高喷射压力和背压下，椭圆喷雾会出现换轴现象.此外还可以发现，换轴距离随着喷射压力的提高而缩短，而换轴次数随着喷射压力的增加而增加.以上结果表明提高喷射压力能够提高换轴频率，加剧椭圆孔喷雾的不稳定性，促进燃料与空气的相互作用.

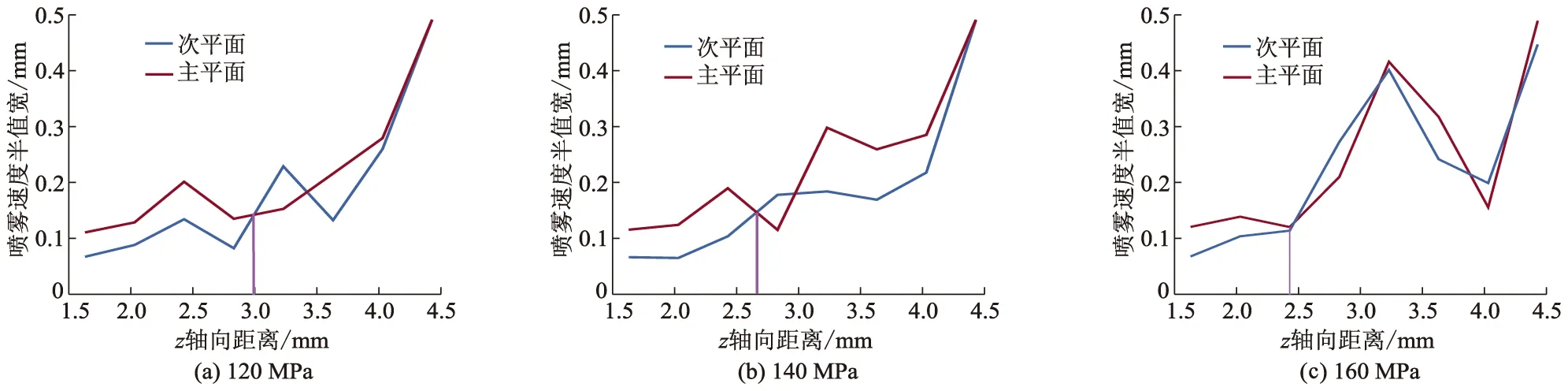
图6 不同的喷射压力下喷雾速度半值宽沿z轴分布(t=20 μs)

为深入分析椭圆孔的换轴现象，在固定背压不同喷射压力条件下，分析了椭圆孔不同平面上的速度大小与流线分布，如图7所示.在图7中，可以观察到在不同喷射压力条件下的主次平面的速度分布轮廓相似，喷雾尖端两侧都存在两个空气夹带比旋涡，并且空气夹带比旋涡随着压力的提高而增大，这表明高喷射压力更易将空气卷入喷雾中.在120和140 MPa主次平面中，可以发现出口处的主平面的速度大小明显高于次平面.这解释了图6中在喷雾初始时刻主平面的喷雾速度半值宽大于次平面的现象.但随着喷雾的发展，由于空气阻力与速度的平方成正比，速度较大的主平面喷雾受到更大的阻力，从而长轴喷雾向两侧的加速度迅速下降，短轴喷雾扩散速度逐渐超过长轴喷雾，次平面的喷雾速度半值宽与主平面达到第1次相同，完成第1次换轴现象.经过第1次换轴后，由于椭圆孔喷雾初始端动能分布的不均匀，导致主次面速度大小不断交替引起多次换轴现象.高喷射压力条件下的这种换轴现象更为突出，如图6所示，160 MPa下出现了4次换轴现象，而120 MPa下只出现了1次换轴.以上结果表明提高喷射压力加剧了喷孔初次破碎动能分布不均匀，提高了换轴频率，优化了雾化效果.

图7 不同的喷射压力和3 MPa固定背压下椭圆喷孔在不同观察平面上的速度大小和流线 (t=20 μs)

为了比较不同视平面上的初次破碎情况，图8给出了不同喷射压力下长短轴面上的液相分数与液相射流的三维分布.由图可以观察到，在高喷射压力条件下喷雾前端的液相质量分数随压力的增大而减少.说明高喷射压力能够加剧燃料与空气的相互作用，加快喷雾的破碎进程.从三维射流图中也可以看出压力越高，椭圆孔喷雾表面波动越剧烈，表面呈现的褶皱越明显，液相燃料更容易破碎.其中在三维图中发现一个特殊现象，即在喷孔出口附近，主面的液相破碎程度一般高于次平面，而在距离喷孔一定距离后，次平面液相褶皱程度会明显高于主平面，液相破碎加剧，且随着喷射压力的提高而愈加越明显.

图8 不同的喷射压力下不同视图平面的液体质量分数和三维液体射流(等值面0.10，t=20 μs)

为研究喷射压力对液相长度的影响规律，对相同背压(3 MPa)不同高喷射压力下初次破碎的液相长度进行了研究，结果表明,不同高喷射压力下初次破碎的液相长度差距较小，这与圆孔喷雾的规律一致.但随着喷射压力的提高，液相末端的液滴会变得越来越少，如图9中红线框所示，在喷射压力160 MPa时，液滴几乎完全消失，这表明喷射压力能够加快液相的破碎过程，加快雾化进程.

图9 椭圆喷孔在不同喷射压力下液体体积分数(等值面0.95，t=20 μs)

涡量大小决定了初始喷雾表面的不稳定性与喷雾液相的破碎速度，所以对近场涡量进行分析是必要的.背压3 MPa下的不同喷射压力时，不同视平面内的涡量大小对比如图10所示.在喷射压力为160 MPa时，椭圆孔内及近场喷雾的涡量在主次平面内明显高于其他喷射压力下的表现，这与喷射压力增强初始湍流扰动性的观点一致.此外发现不同喷射压力下的椭圆孔主次面上的涡量大小不同，但发展趋势与液相破碎的规律相一致.在相同喷射压力条件下，次平面上的涡量大小在离喷孔一定距离后大于主平面相同位置的涡量大小，而涡量大小决定了液相的破碎程度，这可以解释液相破碎时次平面上的褶皱变化大于主平面的现象.同时验证了椭圆孔能够加剧初始喷雾的不稳定性，增大喷雾空气夹带比，优化椭圆孔雾化质量的结论.

图10 背压3 MPa下的不同喷射压力时不同视平面内的涡量

3.2 试验结果分析

为研究椭圆孔初次破碎对喷雾下游的影响，进行了椭圆孔和圆孔的宏观喷雾对比试验，图11为背压3 MPa不同高喷射压力下，圆孔与椭圆孔的喷雾发展历程，可以发现圆孔和椭圆孔的喷雾下游部分，圆孔喷雾在单位体积内的雾化密度明显低于椭圆孔的主次面，且空气夹带比少于椭圆喷孔，椭圆喷孔的雾化效果更好.

图11 背压3 MPa不同高喷射压力下，圆孔与椭圆孔的发展历程

不同喷射压力和3 MPa固定背压下的喷雾贯穿距和喷雾锥角如图12，13所示.由图12可知，喷雾贯穿距随着喷射压力提高而增加，并且圆孔喷雾的贯穿距最终会大于椭圆喷孔.而在图13中，圆孔的喷雾锥角是始终小于椭圆孔.说明椭圆孔形状的不规则性，加剧了初次破碎的不稳定性，增加了喷雾的空气夹带比，使更多空气进入喷雾，扩大了喷雾面积，导致椭圆孔的喷雾锥角大于圆孔；而喷雾表面的扩大，增加空气与喷雾的接触面积，提高了空气阻力，最终导致椭圆孔的喷雾贯穿距小于圆形喷孔.以上可以得到椭圆孔在高喷射压力下可以促进初次破碎，有利于提高二次雾化质量的结论.

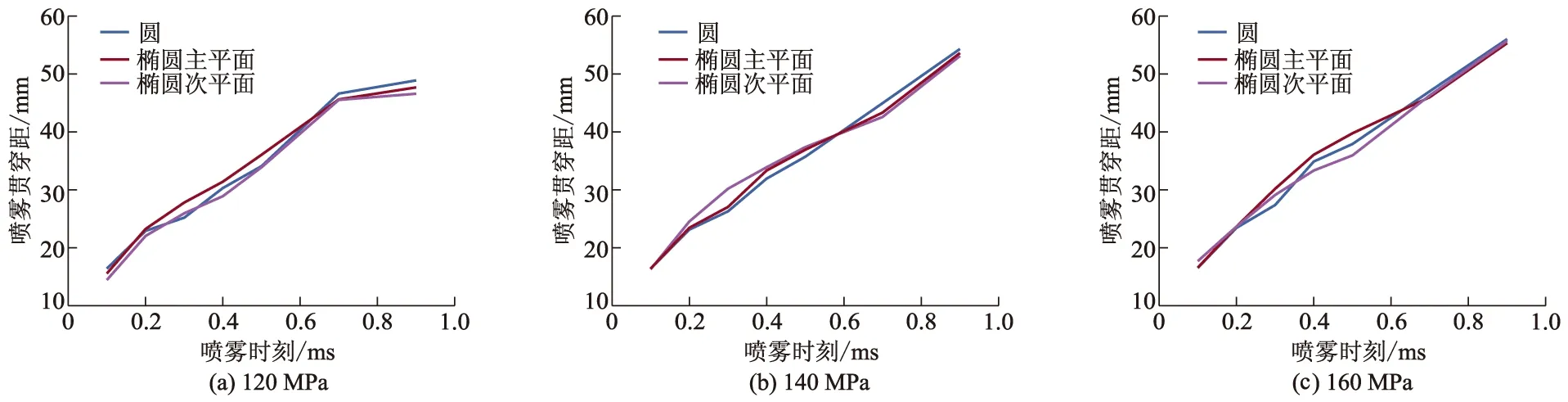
图12 不同的喷射压力和3 MPa固定背压下的喷雾贯穿距

图13 不同喷射压力和3 MPa固定背压下的喷雾锥角

4 结 论

1) 椭圆孔的不规则性决定了喷雾主次平面内初始速度差异.而空气阻力与速度成正比的关系，主平面内的加速度没有次平面大，导致第1次换轴现象的发生，而多次换轴现象，也是椭圆孔的不规则性导致喷雾内部动能不均匀引起的.

2) 椭圆孔初次破碎的液相长度与圆孔规律一致，即喷射压力对液相长度的影响较小，但喷射压力越高越能够加速初次破碎的进程，提高雾化质量.

3) 提高椭圆孔喷射压力与圆孔一样能够增加喷雾贯穿距，但提高喷射压力对其喷雾锥角的影响不大.

4) 椭圆孔结合高压能够加剧了初次破碎表面的不稳定性，加快液相破碎进程，增加空气夹带比，提高空气进入喷雾的含量，提高了喷雾下游的雾化质量.