基于超声波的清除道路压实冰雪理论与方法

张恩惠 李 双

（东北林业大学机电工程学院 黑龙江哈尔滨 150040）

在冬季降雪较多，普遍以浮雪、积雪和板雪的形状停留在路上。四季无雨时期路面的阻碍因数为0.6，雨季路面的阻碍因子小于0.4，在冬天降雪路面仅0.28，结冰路面仅有0.18，路面摩擦因数的减缩导致了汽车制动间隔增长，大大增多了交通事故的涌现。压实冰雪路面致使的交通事故超过其他路面的20%左右，占总交通事故35%以上[1]。因此世界各国对清除冰雪都很重视，针对路面中央大面积的冰雪清除的方法比较全面，路面除冰从压实冰雪接触式和非接触式这两个方向进行，涉及机械清除、热力清除和改良路面铺装材料实行清除[2]。机械法除冰是采用机械动力作用于压实冰雪上，通过刮铲、敲打和碾压等方式使其内部产生应力破坏从而实现冰雪破碎脱离路面；热力融冰效率高，但能耗大，换流设备昂贵，需要合理的电力调度。但是小面积的、路况比较复杂的路边人行道的压实冰雪的清除装置缺乏严重，而采用人工铁铲清除的方式处理，但是将损耗大批的人力，财力和时间，并且成效极低[3-4]。超声波除冰方法也为机械除冰方式，其结构简单、耗能低、费用低、重量小等好处。因此，越来越多的研究者专注于这种方法。例如，Palacios、Habibi和朱等研究了几十年的超声波除冰技术为飞机、风力涡轮机设计了几种超声波除冰或防冰系统[5]。然而对超声波除冰机理的研究还不是很全面。在大多数研究中，除冰准则被认为是一个静值：如果压实冰雪界面横向剪应力幅值超过了通过静态张力测试确定的粘着强度，那么除冰系统是可行的[6-7]。因此研究利用超声波的高频振动清除压实冰雪技术在人行道上的应用对路面的保护、清除效率高具备重要的意义。

一、超声波清除压实冰雪和脱离路面准则理论

（一）超声波清除压实冰雪原理。超声波换能器产生的电能转变为机械能会以Lamb波和SH波的形式在压实冰雪路面中传播[8]。兰姆波是超声波板波的一种形式，压实冰雪路面中的高频振动是由横向波和纵向波叠加致使的，而且振动粒子的轨迹是椭圆的状态的。同时SH波是一种简单的谐波。当这些超声波在多层板（压实冰雪/路面层结构）中传播时，速度视差将由压实冰雪层路面层之间的不同密度引起的如图1所示。紧接着，将形成压实冰雪和路面层界面之间的剪切应力，如果该界面中的微缺陷是由剪切应力累积到一定程度引起的（（三）中讨论）。压实冰雪将破碎成碎片并从路面上分离出来。

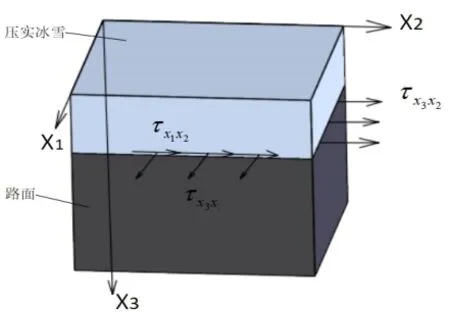
图1 超声波在具有压实冰雪层的路面中传播

压实冰雪路面表面波动的控制方程：

式中：σij是应力张量分量；xi是空间坐标分量；ρ是材料的密度；ui是在i方向的位移和t是时间。由胡克定律知几何方程和刚度张量的对称性给出：

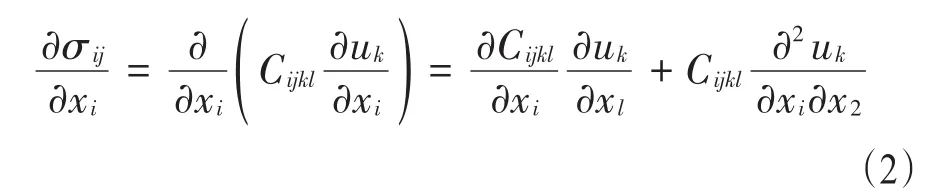
式中，Cijkl是刚度张量分量；将方程（1）代入方程（2）获得压实冰雪与路面层结构的超声波传播的控制方程：

方程（3）表示关于未知位移场的偏微分方程组。在实际应用中，路面上的压实冰雪面积通常比较大，因此在超声波除压实冰雪系统中，通常采用多个超声波换能器发射振动共同作用，存在五个带有压电元件圆锥形换能器（将高频电能转化为机械振动的装置），将其固定在超声波除冰装置上。不仅机械边界条件外，而且压电边界条件。这些条件是机械振动位移和超声波的相互作用[9-10]。被驱动的压实冰雪部分是一个区域而不是一个点，而每个点在这个区域的移动是不同的。因此，方程组的边界条件取决于换能器与压实冰雪接触时的运动状态。这种振动非常复杂，很难用公式来描述。因此，本文采用一定的数值方法求解高频振动最佳频率和应力场。

（二）分离度定义和演化方程。压实冰雪的剥离是一个渐进的过程，可以通过连续损伤力学来描述。损伤力学的重要概念是从1958年Kachanov研究金属蠕变破坏时提出材料损伤的概念。在接下来的几十年里，损伤力学的概念被发展成为解决材料或结构在外部载荷作用下的延性、蠕变、疲劳和脆性破环的有效理论[11]。该理论将失效视为一个连续的过程，用损伤变量来定量描述断裂程度。首先定义压实冰雪从路面的剥离度，形容压实冰雪与路面界面之间粘附力的破坏程度；最后用除压实冰雪系统的参数和应力阈值，超声波在覆压实冰雪路面中传播，通过数值模拟可以预测剥离过程。

针对超声波除压实冰雪的问题，为了描述压实冰雪与路面界面的局部破坏程度，基于损伤力学方法定义剥离程度D：

式中：D是为0～1的字段标量变量0≤D≤1，当D=0时，界面是理想的粘结面；当D=1时，界面失效，给定位置的压实冰雪被完全移除。由于D在除压实冰雪过程中依赖于空间位置和时间，所以它是空间坐标和时间的函数。相比之下，由于D是定义二维平面的（界面），所以3个坐标分量x1,x2,x3是不独立的，假定界面的曲面方程为：

脱离程度D可由2个坐标和时间变量t独立确定：

在超声波清除压实冰雪装置作业进程中，后段的剥离程度D会发生演变。要解决的问题是连续损伤累积[12]。在这基础上，应用损伤累积速率的演化方程。界面剥离程度的累积速率主要取决于施加的剪切应力，根据模拟得到的剪切应力幅值与时间的关系，可以建立演化方程为: 当τ|interface ≥τtℎ时：

式中：τ|interface是压实冰雪层与路面界面上的剪切应力幅值；τtℎ是应力阈值；等于粘结强度。此外，a和m是分离参数。剪切应力幅值大于应力阈值是脱冰原因，有效应力为τ(=τ|interface-τtℎ)，显然的，当τ|interface ＜τtℎ时

由式（8）可知，存在剪切应力幅值小于应力阈值，压实冰雪从路面界面的剥离进度不能累积。这就意味时间对除冰系统无关，压实冰雪不会从路面上分离出来，压实冰雪路面的应力阈值作为黏附强度（1.35Mpa）。

（三）压实冰雪脱离路面准则。有些实验结果表明，在超声波换能器发射时，基片上的积冰会裂成小块。由于这些小块的冰块会相互分离，界面的局部破坏会导致压实冰雪的脱落。因此，对于界面上假设的点，局部压实冰雪脱离准则为：

其中T是压实冰雪脱离的时间消耗，将式（7）代入式（9）得：

清除压实冰雪的总的时间是界面失效大部分区域的时间消耗。对于应力分布集聚的界面，这种损伤累积模型可以预测压实冰雪的剥离行为[13]。超声波清除压实冰雪的效果决定于超声波换能器激发的电能转变为机械振动。所以结构的振动有限元方程为:

式中：为施加的机械应力为外部激励电流为弹性位移场;Φ为电势强度;[Kuu]为弹性刚度矩阵；[KuΦ]为压电刚度矩阵；[KΦΦ]为介电矩阵；M为质量矩阵;R为耗散矩阵；ω为角频率。

二、超声波清除压实冰雪过程的仿真分析

通过有限元的谐波分析对模型进行模拟，可以得到超声波振碎压实冰雪的最佳频率以及应力场并能获得压实冰雪模型在超声波振动过程中的各个时间节点的损伤变化情况，包括初始裂纹出现的位置、裂纹扩展形式及压实冰雪损伤程度。

（一）定义材料参数及有限元建模。在进行数值模拟时，PZT-4材料参数如下介电系数矩阵：

压电的刚度矩阵：

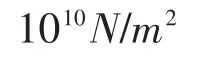
压电矩阵：

将超声波换能器采取ANSYS软件中的实体SOLID5单元实施网格划分，选取200mm×200mm×20mm的压实冰雪道路作为模型，压实冰雪和沥青路面采取实体SOLID45单元实施划分网格，划分的网格如图2所示，理论上划分的网格越小计算精度就越高。但是，如果元素太小，会导致计算效果很差，所以经过收敛计算，该模型的单元个数和节点分别为6894和35648，材料性能参数如表1所示。

图2 模型网格划分

表1 材料的各项性能参数

（二）破碎压实冰雪的最佳频率和应力场。谐波响应用于明确非线性和线性结构承受简谐载荷变化时的稳态响应，设超声波高频振动以一定的简谐频率载荷作用于压实冰雪路面，研究压实冰雪路面的稳态响应，其通用的方程：

力矩阵[F]和位移矩阵{u}是简谐的，频率为ω，以复数形式表示为：

式中：Fmax为力幅值；φ为力函数的相位角；实部F1=Fmaxcosφ；虚部F2=Fsinφmax；umax为位移幅值；φ为位移函数的相位角；实部u1=ucosφmax；虚部u2=usinφmax。谐响应分析的运动方程：

超声波振动的频率是已知的，作用力F确定后可以得出压实冰雪路面在确定频率下的位移曲线和超声波共振频率下的最大位移响应和最大应力场。

通过有限元软件ANSYS进行谐波分析得到超声波除压实冰雪的频率,然后对压实冰雪路面有限元模型施加固定约束和位移载荷，模型的路面不与压实冰雪粘结其他五个面采用全约束（AllDOF）,正弦曲线的振幅施加在换能器正极上的电压为100v,而施加在负极上的电压为0[14]。该电激励信号表示为：

其中U(t)是施加在换能器上的电压；f是电压的频率；t是时间；φ0是初始相位。

设定加载子步为80步，加载频率从20KHz到100KHz,步长为100Hz，位移载荷设置为Z方向的15um，用完全法（Full）求解[15]。由图3可以看出，在每个节点中，不同的频率，所产生的破碎应力不同，在压实冰雪的不同节点处，产生的最大破碎应力不同，最佳的破冰频率也有所差别，超声波振动频率对压实冰雪产生共振的点有多个，但是选用的超声波换能器的谐振频率为40kHz,而压实冰雪表面、边界、顶点、中间以及路面与压实冰雪界面节点产生简谐共振频率的且小于超声波换能器频率的大概在27.2kHz，则超声波破冰的最佳频率为27.2kHz。

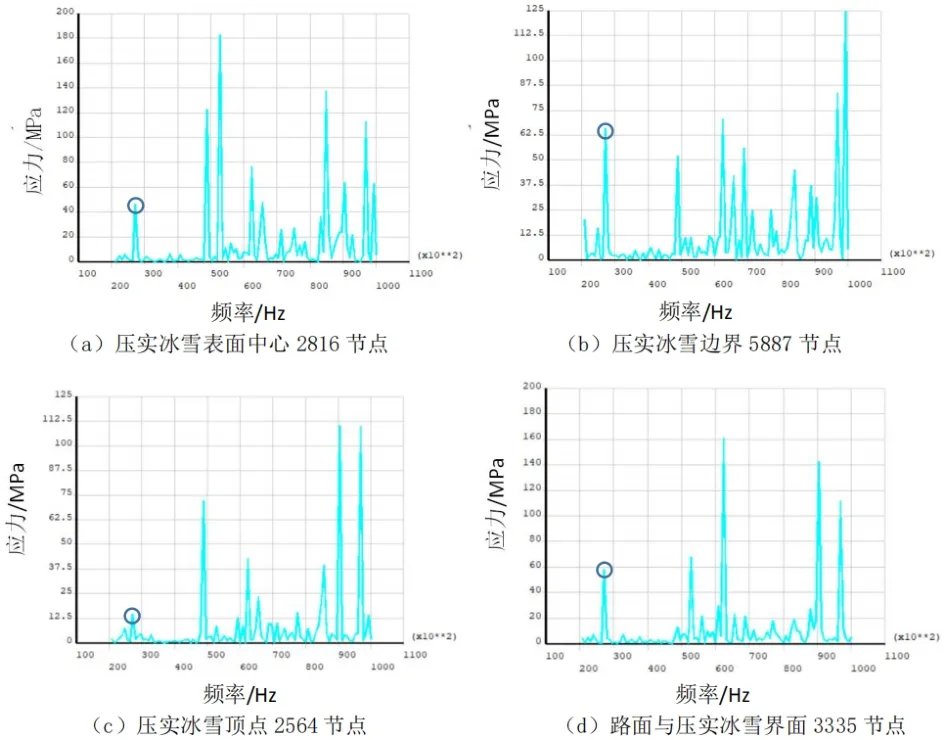
图3 频率-节点应力曲线图

在压实冰雪脱离路面仿真模拟中，选择该频率作为最佳频率。在27.2kHz频率下节点处的应力场云图如图4所示。由图可以看出，最小应力和最大应力都超过了压实冰雪与路面间的粘附强度，达到破碎压实冰雪的效果，其次最佳频率下的总应力云图如图5所示。根据这些应力分布，剪切应力较高的在压实冰雪表面放置超声波换能器周围和中间的区域，将图5中颜色顺序的最后一步值作为大部分区域的最小应力。如图5所示，大部分区域的应力都大于该值，这就意味着当该应力区域的压实冰雪脱离时，大多数沥青路面上的压实冰雪层依然被清除。因此，我们用这个应力作为判断整体清除压实冰雪时间的标准。

图4 27.2kHz下XY平面剪切应力场

图5 27.2kHz总应力云图

（三）不同超声波参数清除压实冰雪路面的效果。在破碎压实冰雪时，路面上的压实冰雪多数为大面积的，由二（二）节仿真分析结果得到最佳共振频率为27.2kHz，由于人行道中的压实冰雪都是粘附强度比较高的，所以对于面积较大的路面，采用多个超声波换能器连接变幅杆的工具杆共同作用于压实冰雪界面，对压实冰雪同时给与相同频率为27.2kHz的不同振动点，如图2所示，依次在压实冰雪面上施加1个、2个、3个、4个、5个作用点施加相同的频率振动，得到相同频率振动下的不同振动点的压实冰雪应力值，如图5所示，由图4可知，在压实冰雪路面上施加的频率振动作用点个数增加，每个节点在Z方向产生的压缩应力值和在XY平面上的剪切应力值都是先增加再减小，最后趋于平稳。而当同时施加5个激励作用点时，Z方向上的压缩应力和XY平面上的剪切应力值最大，因此对压实冰雪路面的除冰效果最好。

当给与的共振频率和振动点个数一致时，施加的不同超声波幅值时压实冰雪路面节点处出现的Z方向上的压缩应力和XY平面上的剪切应力值的变化如图6所示。由图6可得，幅值增大时，压实冰雪路面的每个节点竖轴方向上的压缩应力和XY平面上的剪切应力也随时增加再减少，最后趋于平稳，使得路面上压实冰雪破碎有更好的效果[8，16]。但是过高的振动幅值会造成路面的损坏，由图7可见，振幅为15um时，竖轴方向的压缩应力和XY平面上的剪切应力值较为平稳，而且压实冰雪路面节点上的压缩应力和剪切应力都超过其压实冰雪破碎应力和粘结应力,更能破碎压实冰雪。

图6 压实冰雪路面中不同作用点处的压缩应力和剪切应力值的变化

图7 不同幅值下压实冰雪的压缩应力和剪切应力值的变化

三、结语

本文探究了超声波高频振动作用下对路面压实冰雪进行清除的方法与理论，应用超声波的损伤积累理论分析和仿真分析超声波对压实冰雪破碎的效果。运用ANSYS有限元软件对压实冰雪路面实施了谐波分析，得到了破碎压实冰雪层的最佳频率为27.2kHz;并研究了不同超声波幅值、不同振动点对压实冰雪破碎的影响，得出15um幅值和5个振动点对压实冰雪的破碎效果最好。