基于四组对比模型的线圈式电磁炮弹丸速度分析

邱 立 范雨薇 张 龙,3 易宁轩 邓 奎 田金鹏

(1.三峡大学 电气与新能源学院,湖北 宜昌 443002;2.梯级水电站运行与控制湖北省重点实验室,湖北 宜昌 443002;3.武汉中原电子信息有限公司,武汉 430074)

伴随着当代武器系统的发展和航天探索的强烈需求,对使用特定手段将物体快速推进到一定速度有着愈发普遍的需求和更加深入的研究[1].在相同条件下,炮弹的出口速度越大,射程越远,弹体接触目标后的击伤能力愈发强大[2];火箭如果能在点火前获得一个初始速度,其发射初期受到外界环境因素的影响将会减小,在发射过程中达到既定速度的时间将会更早,且能减少自身携带的燃料,提高有效载荷占比,其发射效率与经济性将会显著提高[3].电磁发射作为一种新型的发射方式,以洛伦兹力作为载体,能够在发射阶段使弹丸获得极高的初始速度,或在火箭升空过程提供一定的初始发射速度.前者对于炮弹突防、提升穿透强度有着重要的意义,后者对于火箭的快速部署、稳定发射有着良好的应用潜力.电磁炮是利用电磁发射技术制造的一种先进动能杀伤武器.此外,电磁炮有着隐蔽性良好、弹药易于储存制造、单次发射成本低等先天优势[4-6].

根据电磁发射的特点,电磁发射装置分为3种类型,分别为线圈式、导轨式、重接式.线圈式电磁发射装置理念较为完备,相比于其他两种类型而言,有弹体与发射管无接触、无导轨烧蚀现象、工作寿命长等特点[7].在金属加工或工业生产方面,线圈式电磁发射装置的脉冲技术可以应用于金属的电磁成形[8-9],降低传统机械成形过程中的能耗与污染,且电磁加工方法各个参数调制方便、重复性好.但是,在线圈式电磁发射装置的实战部署方面,仍然存在着若干待解决的问题,如主电路工作电压相对较高,发射行为调控难度大,电能使用效率较低等不同因素的相互制约[10],使得出口速度指标并不完全尽如人意[11].作为一个耦合电磁场、结构场、温度场等多物理场的复杂物理行为,弹丸经过电磁发射的出口速度与系统若干因素均存在关联[12-13].目前的研究基本上是从全耦合角度出发,没有把由于弹丸位移造成的磁场衰减和弹丸运动造成的动生电动势两个因素进行解耦建模分析.

本文利用有限元分析方法,建立4个分析模型,使得对弹丸速度的影响因素处于解耦分析状态,目的在于分析线圈式电磁发射过程中磁场衰减和动生电动势对弹丸运动的影响.

1 基本原理与分析方法

线圈式电磁发射装置的原理如图1所示.线圈炮发射装置主要包括储能电容器、主放电开关、驱动线圈、电枢等.当储能电容器储存足够的电能后,闭合放电开关向驱动线圈通电形成脉冲电流,在线圈周围产生脉冲磁场.根据电磁感应定律,变化的磁场将在驱动线圈附近的电枢中产生感应电流,在感应电流和脉冲电流的斥力作用下,驱动弹丸.其中,由功率二极管和续流电阻串联构成的续流回路,在放电电容的电压正负极性反转时,为驱动线圈中的剩余能量提供流通通路,从而减小驱动线圈中的电流幅值,降低线圈由于过大的脉冲电流的热效应而产生的温度升高,以此来提高驱动线圈的热稳定性,以达到延长发射装置使用寿命的目的[14].

图1 线圈型电磁发射装置原理图

驱动线圈与弹丸电枢的磁路耦合可以由图2所示的等效电路表示.

图2 驱动线圈与弹丸电枢磁路耦合的等效电路

根据电路各等效参数VCR 关系,此时可以得出:

式中:ecoil-coil和ecoil-a分别为驱动线圈电流产生的磁场发生变化时,在线圈回路自身产生的感生电动势和在弹丸中产生的感生电动势;ea-a和ea-coil分别为弹丸涡流产生的磁场发生变化时,弹丸自身产生的感生电动势和在线圈回路中产生的感生电动势;Icoil表示驱动线圈中所流通的电流;Ia表示弹丸电枢中生成的感应涡流;Lcoil表示驱动线圈的自感参数;Ia表示弹丸电枢的自感参数;Mcoil-a与Ma-coil表示驱动线圈与弹丸电枢线圈之间的互感,通常两者相等,下文以M表示.

由上述推导分析,线圈式电磁发射装置的工作电路可以满足如下关系:

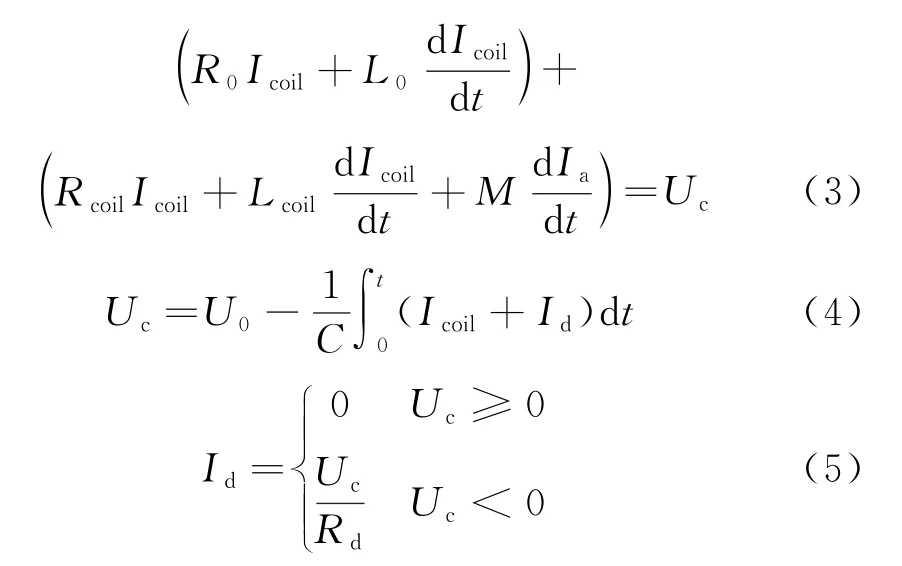
式中:Uc表示电容电压;U0为电容的初始放电电压;Icoil表示驱动线圈所在支路流通的电流;Id表示续流支路电流;Rd表示续流支路串联电阻;Rcoil,Lcoil分别表示驱动线圈对应的等效电阻与电感参数;R0表示线路等效电阻;L0表示线路等效电感.

线圈式电磁炮的驱动线圈一般为螺线管线圈,忽略其渐近线的影响,则螺线管线圈可以等效为多个在相同轴线分布的闭合同尺寸金属圆环.在本文的分析中,以弹丸发射的运动方向作为轴向正方向,垂直于弹体发射方向为径向方向.驱动线圈中所流通电流与弹丸电枢中的感应涡流均由环向分量占主要成分,两电流方向相反,但其在线圈与弹丸电枢之间的间隙内产生的磁场径向分量方向相同,磁场方向都垂直于对称轴,两电流激发的磁感应强度在此得到叠加.

由麦克斯韦方程,可得到如下等式:

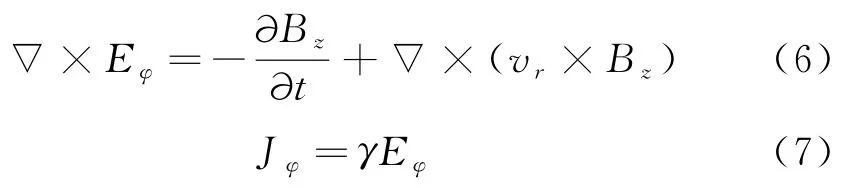
式中:E表示分析区域内的电场强度;J表示驱动线圈与弹丸电枢内的电流密度;B表示分析区域内的磁感应强度;v表示弹丸运动的实时速度;γ表示材料的电导率.各个物理量存在着环向分量φ、径向分量r、轴向分量z.通过式(6)等号右侧第二项可以看出,磁场变化与弹体运动均会对环向电场强度即电流密度产生影响.

在驱动线圈与弹丸电枢线圈的微分析域中,每一个微元被加载的电磁力由该处的电流密度大小与所对应的磁感应强度共同影响:

由式(8)可得,各微分析域中轴向电磁力由分析区域中径向磁感应强度和该区域对应实时产生的环向感应电流密度决定;同样,由式(9)可得,各微分析域中径向电磁力由分析区域中轴向磁感应强度和该区域对应实时产生的环向感应电流密度决定.在分析中,一般将弹体视为刚体,且各部件在径向方向受到的电磁力合力为0.

弹体的速度可由下列等式计算得出:

式中:vz代表弹体轴向方向运动速度;Iz代表弹体轴向电磁脉冲冲量;m为弹体质量.

电磁发射是一个有着电磁场、结构场、温度场等的强耦合过程.尽管在本文的分析中并没有考虑电流热效应带来的热量流通,但其已经属于一个复杂的多物理场耦合求解问题.有限元法是目前分析电磁发射物理过程的主要方法之一[15-16].在本文分析中,有限元仿真软件的计算流程如图3所示.其中,包含了以下4个存在相互关联的物理场.

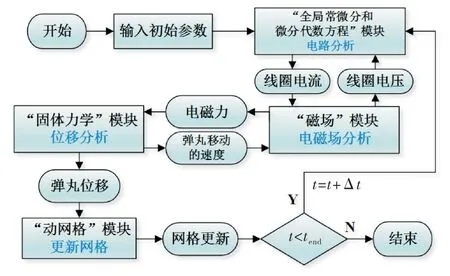
图3 有限元软件的仿真计算流程图

1)“全局常微分和微分代数方程”模块

对于线圈式电磁炮的工作电路进行实时解析,其对仿真过程中式(3)～(5)进行计算,以计算电路工作状态,获得各个支路中元器件加载电流电压的实时数值,为后续“磁场”模块的电磁场分析提供参数注入,计算中使用到的电路参数见表1.

表1 有限元仿真计算中使用的电路参数值

2)“磁场”模块

在驱动线圈中加载电流之后,处于驱动线圈相邻处的四周空间内将会产生磁场,造成通过弹丸电枢的磁通发生变化,在弹丸电枢中产生感应电流以及动生电动势.

3)“固体力学”模块

弹丸电枢在磁场的作用下将会受到电磁力加载,使得弹丸在轴向方向发生移动.

4)“移动网格”模块

用来在每个计算时间步内更新因弹体位移而变化的网格.

2 线圈式电磁炮四组对比模型的搭建

线圈式电磁炮在发射过程中,随着弹丸与驱动线圈之间的距离增大,弹丸所处的磁场逐渐衰减,使弹丸电磁力减小.在弹丸受到电磁力驱动时,产生动生电动势,其作用为阻碍弹丸的运动.动生电动势还会通过影响涡流反作用于驱动线圈产生的磁场,导致磁场分布与电磁力分布发生变化.结合式(9),弹丸运动将从两方面对弹丸所受电磁力与出口速度产生影响:一为弹丸由于位移远离驱动线圈,造成的所处磁场衰减;二为因弹丸运动产生的动生电动势,造成弹丸中感应涡流发生变化,影响所受电磁力.因此,本文建立4种模型进行对比分析,为了避免因为加载电流不同造成模型失去可比性,对各个模型施加相同的电流,模型如下.

1)静止模型

该模型是不考虑弹丸位移和速度的瞬态模型.在静止模型里,仅对弹丸电磁发射过程做了电磁分析,即弹丸相对于驱动线圈而言固定不动.由于没有真实的运动速度,不包含动生电动势对弹丸电枢所造成的磁场和涡流的影响,最终得到弹体理论的位移和速度.

2)位移模型

模型中弹丸在每一个有限元分析的时间步计算完成后,都会受到电磁力的加载,因为弹丸并未固定于某处,所以可以求解得到其运动方程.在下一个时间步开始前,弹丸的位移更新到新计算得出的位置.因此,位移模型存在着弹丸位移与磁场衰减的因果关系.由楞次定律可知,动生电动势产生的感应涡流,会减慢弹丸的速度.由于位移模型没有考虑动生电动势的影响,所以较完整运动模型而言,弹丸的速度将会更快.

3)速度模型

模型将弹丸相对于驱动线圈进行固定,解耦位移因素对于弹丸的影响.通过在弹丸求解域内增加式(6)中的右边第二项,引入动生电动势对磁场分布的影响.在速度模型中可以计算出动生电动势,从而实现了将弹丸运动速度对弹丸所处的磁场和电磁力产生的影响纳入考虑.因为该模型中的弹丸同样保持静止,无由位移带来的磁场衰减对Br的影响,所以弹丸产生的动生电动势比完整运动模型中的更大,即对于磁场和电磁力的影响也越大.

在此需要指明:前3个模型仅为了可以更方便地解耦分析,其相对应的运动情形不是真实存在的.但可以对影响电磁发射运动过程的因素进行详细地解耦分析,对理解发射机理具有积极的作用.

4)完整运动模型

该模型为真实存在的弹丸实际运动模型.作为一个完整的电磁运动模型,同时考虑了弹丸由位移造成的磁场衰减和由速度造成的动生电动势对弹丸运动的影响.

上述模型只有完整运动模型可以表达出弹丸实际运动过程;而建立另外3个模型,可以解耦速度和位移两个影响因素,单独观察两者对于弹丸运动的影响;对比静止模型和位移模型,得到位移对运动过程的作用;对比静止模型和速度模型,得到速度带来的动生电动势对运动过程的作用;观察完整运动模型,得到位移和速度两个因素的作用.

为了能够更好地对影响弹丸电磁力及运动过程的因素进行分析,对分析模型做出如下设定:(1)电流载荷为一脉宽为tc、峰值电流为Imax的半个周期的正弦波;(2)运动过程中视弹丸为刚体,即不存在形变行为;(3)忽略除电磁力以外的其他任何载荷力(如空气阻力、摩擦力等).

3 仿真结果分析

创建上述4种对比分析模型.在各模型计算完成后,对计算数据进行后处理,对所得结果进行分析.

3.1 弹丸电枢内的涡流分析

在4种对比模型中,弹丸位移造成的磁场衰减和弹丸运动产生的动生电动势都直接影响到弹丸内的涡流分布.图4给出了电流峰值时刻各个不同模型中弹丸电枢内感应涡流电流密度分布云图.

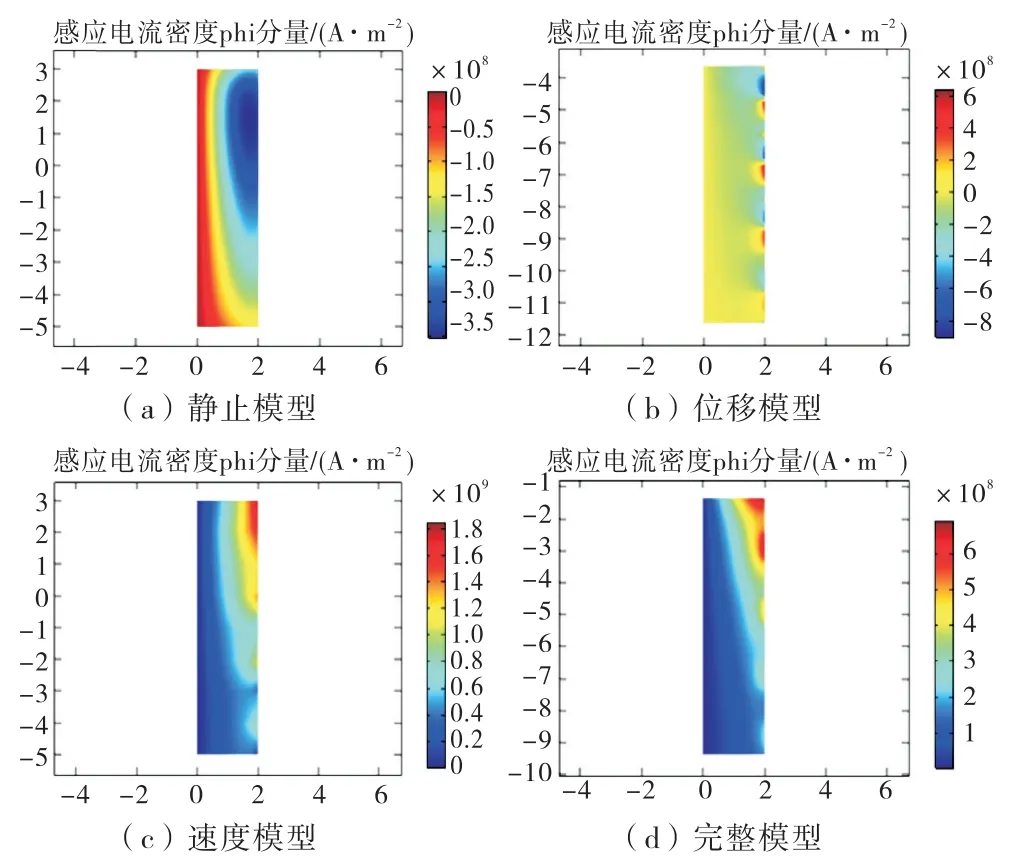
图4 不同模型中电流峰值时刻弹丸涡流分布云图

对比静止模型与速度模型,发现在一定范围内两者电流方向相反,推测速度模型所受电磁力发生改变,即电磁力开始减缓弹丸的运动速度.对比速度模型和完整模型,发现两者电流密度分布趋势类似,即动生电动势在支配感应电流分布的过程中会发生作用,使得速度模型中的涡流分布更接近于实际的完整运动模型.

通过在弹丸区域内对电流密度进行积分,得到4种对比模型中弹体内的感应涡流随时间的变化,如图5所示.

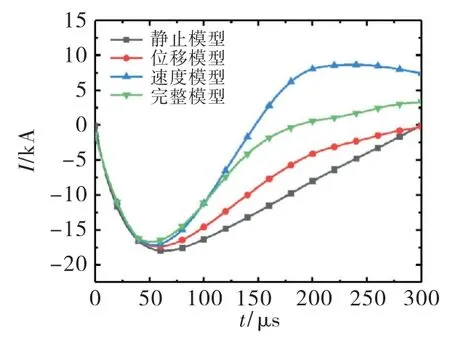
图5 不同模型中的弹丸感应涡流

感应涡流一开始为负,是因弹丸内的感应涡流与线圈中的电流方向相反.对比分析静止模型与位移模型或速度模型,静止模型中的感应涡流幅值最大,即在考虑弹丸位移或者动生电动势时,弹丸中的感应涡流均存在衰减现象.对比分析速度模型与完整运动模型,由于速度模型没有考虑位移因素,使得动生电动势在更大的磁场作用下幅值更大,而动生电动势会导致涡流衰减,即造成速度模型中感应涡流的衰减速度比完整运动模型更加显著.

3.2 模型的磁场分析

由于弹丸中的涡流分布存在差异,所以造成了各个分析域内的磁场也存在差别.图6给出了电流峰值时不同模型中的弹丸电枢内磁通密度模分布云图.

图6 不同模型中电流峰值时刻电枢磁通密度模分布云图

由图6可知,位移模型磁通密度模的最大值较小,即位移会带来很大的磁场衰减.而速度模型较完整模型存在更大的动生电动势,所以磁通密度模的最大值较静止模型较小.完整模型在两因素的共同作用下,磁通密度模的最大值在位移模型和速度模型之间.由于驱动线圈较弹丸相比几何尺寸较大,且弹体位移与自身尺寸相比比值亦较大,驱动线圈表面中心处的磁场受电枢感应涡流影响相对较小,但是其影响相对存在,不能忽略.

图7展示了4种模型里驱动线圈的下表面中心处磁通密度随时间的变化规律.由于涡流与驱动线圈电流方向相反,即涡流幅值越大,在线圈中心处的磁场将会越小.

图7 驱动线圈下表面中心处的磁通密度

由图5知,静止模型的感应涡流幅值最大,故静止模型的中心磁场最小.比较静止模型和速度模型,在电流前半个波形中,静止模型比速度模型的感应涡流大,故其中心磁场较后者更小;在电流后半个波形中,速度模型受到动生电动势的影响,所以其运动速度在动生电动势的减速趋势下将慢于静止模型,而较小的速度又会产生较小的动生电动势,较小的动生电动势带来较小的涡流抵消,故速度模型中的感应涡流较大,即在中心处的磁场小于静止模型.

为了进一步分析磁场的分布,图8、图9是处于电流峰值时刻Br和Bz的分布规律.

图8 电流达到峰值时驱动线圈下表面0.5mm 处径向方向磁场分布规律

图9 电流达到峰值时驱动线圈下表面0.5mm 处轴向方向磁场分布规律

速度模型与静止模型对比,其感应涡流较小,即相对涡流对磁场的影响也较小.在驱动线圈下方的区域内,弹丸电枢磁场与线圈磁场的Br同向叠加、Bz反向抵消,所以速度模型中Br小于静止模型值,而Bz大于静止模型值.

3.3 弹丸受到的电磁力分析

图10为4种对比模型中弹丸受到的电磁合力情况.比较电磁合力的峰值,静止模型＞位移模型＞完整运动模型.

图10 弹丸受到的电磁力

与完整模型相比,速度模型并未考虑磁场随位移产生的衰减,所以速度模型中动生电动势对磁场和电磁力的影响较完整运动模型更大.其在运动初始阶段由于处于更大的磁场中,从而受到的电磁力比完整运动模型大;但在靠后阶段,因为大的磁场和大的运动速度带来了大的反向动生电动势,使得感应涡流较小,导致在后续阶段速度模型电磁力比完整运动模型更小.同时,在较大的磁场影响下,弹丸电枢中存在较大的动生电动势,该作用导致速度模型在运动的后期过程中感应电流有较大程度的反向,电枢电磁合力将会出现较大的负值.

3.4 弹丸的运动速度分析

图11、图12是4种对比模型中的弹丸速度随时间的变化规律.为了探究磁场衰减和弹丸运动两因素对弹丸速度的影响规律,在原仿真基础之上,还选取另外一个电流峰值进行仿真计算.

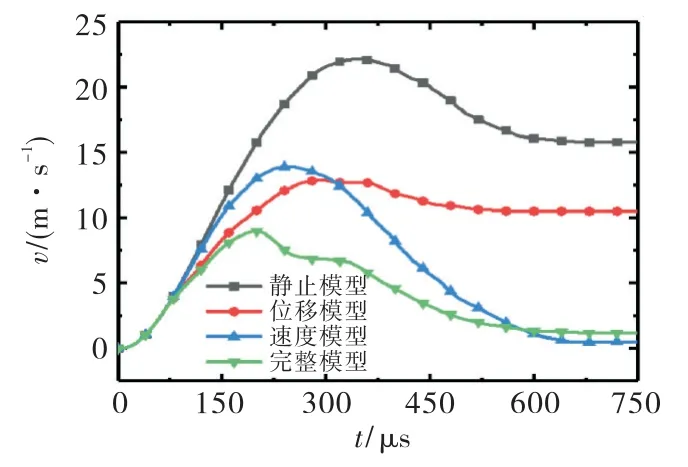
图11 电流峰值为12kA 的弹体速度变化趋势

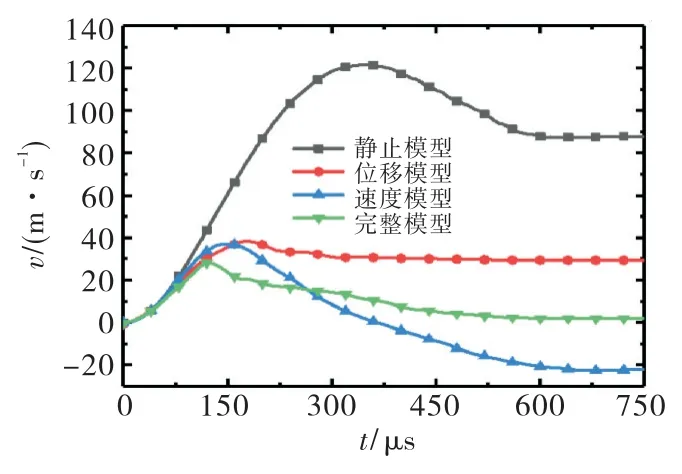
图12 电流峰值为28kA 的弹体速度变化趋势

峰值电流Imax为12kA 时,弹体速度较低(小于22m/s),速度随时间的变化结果如图11所示.可以看出,此时完整运动模型弹丸出口速度明显小于静止模型,静止模型和位移模型曲线相似,速度模型与完整运动模型曲线相似,速度模型中弹体在拖拽力影响下出口速度较峰值速度变化幅度最大,其变化率为96.2%,但是速度模型出口速度已经与真实运动情况下的完整运动模型结果相当;位移模型出口速度较峰值速度变化率为19.5%,但是与真实运动情况下的完整运动模型的数据还有较大差别,这表明虽然低速运动时弹体位移与动生电动势对弹体速度均有影响,但是动生电动势对弹体速度的影响占据主要作用.

当峰值电流Imax为28kA 时,各个模型中弹丸的运动速度较小电流情形更高.其中静止模型的弹丸出口速度最大,位移模型、速度模型、完整运动模型的弹体出口速度较为接近,完整模型的速度最小.在反向电磁拖拽力的影响下,速度模型中的弹体速度已经反向,其出口速度较峰值速度变化率为159.4%.此时,弹体位移和动生电动势共同影响工件速度,两者影响幅度均较为显著.

4 结语

在感应型线圈式电磁发射器的发射过程中,弹体电枢所处的磁场环境与所加载的电磁力大小主要涉及两个因素:第一,因弹丸运动产生的动生电动势;第二,因弹体位移远离驱动线圈导致的磁场衰减.通过对比分析4种有限元分析模型发现,当线圈电流加载较小时,弹丸运动速度较小,动生电动势对弹丸速度影响占据主导作用;当线圈加载电流较大时,弹丸速度相对较大,须同时考虑弹体位移与动生电动势的影响.