基于互补经验模态分解法的高压直流输电线路故障测距
2021-05-28邹红波伏春林高沈清
邹红波 伏春林 高沈清
(1.三峡大学 电气与新能源学院,湖北 宜昌 443002;2.三峡大学 新能源微电网湖北省协同创新中心,湖北宜昌 443002;3.国家电网 巴中市供电公司,湖北 巴中 636600;4.上海蓝科石化环保科技股份有限公司,上海 201800)
我国地域辽阔,但电力能源基地和负荷中心呈现出逆向分布特性,主要能源集中在西部和北部地区,负荷中心分布于东部和南部.为了解决能源远距离、大容量的供应问题,我国大力建设和发展高压直流输电(high voltage direct current,HVDC)工程[1].高压输电系统的故障大多来源于线路故障,对于瞬时的线路故障一般可通过自动重合闸进行故障排除;对于永久性的线路故障,自动重合闸发挥不了作用,需要寻找线路发生故障点的位置并排除故障因子[2].发展和提高高压直流输电线路的继电保护水平对于维护电力系统稳定和安全的意义重大.因高压直流线路的电压没有过零点并且输电线路没有分支,使得故障行波幅值大、受干扰小,因此行波保护是现代高压直流输电线路保护的研究热点[3-6],而行波保护的关键在于故障行波中奇异特征的提取.
故障行波序列具有强烈的非线性、非平稳特征,由多个模态信号组成.将原始信号分解出各个模态信号,对重要模态进行分析,才能准确地提取故障特征信息.常见的分解方法有经验模态分解(empirical mode decomposition,EMD)[7-9]、集合经验模态分解(ensemble empirical mode decomposition,EEMD)[10-13]、局域均值分解[14-17]、变分模态分解[18-20],对原始信号分别解析出不同种类的本征模态函数(intrinsic mode function,IMF).
针对经验模态分解法存在着分解分量过于平滑和集合经验模态分解法分解分量的噪声分量残余过大的问题,本文利用集成集合经验模态分解(complementary ensemble empirical mode decomposition,CEEMD)的方法分解故障行波信号,避免了分解模态分量的过平滑、噪声残余问题,使得其中高频分解模态分量更能反映出高压直流输电线路故障信息,采取双端测距法获取线路故障发生位置.仿真结果表明,该方法线路故障测距精度高、耐受过渡电阻能力强.
1 HVDC线路行波的波头测距原理
高压直流输电系统发生故障后,需要依据线路端的电气量测判线路是否发生区内故障.只有确定为线路发生故障,其线路故障点定位才有意义.线路区内与区外之间存在有平波电抗器和直流滤波器组成的装置,起着高频阻波的作用.根据线路区内外故障后的电气量保护的高频能量差异大的原理,获取故障行波的高频Hilbert能量值判据方法判定故障是否发生于线路上.
当线路确认为区内发生故障后,在故障的行波阶段,控制系统来不及动作(动作时间在10ms以上),线路两侧测得的电压行波不受控制系统的干扰,所以一般选择故障后10ms的数据窗,来获取准确的行波信息并诊断故障的类型和距离.
依据捕获行波波头时间的定位方法主要有双端行波测距法和单端行波测距法.此类方法需假设:电压电流行波的传播速度在直流输电线路中保持不变.
1.1 单端测距法
单端测距法依靠线路一端的量测,利用行波在边界阻抗不连续点发生的反射和折射原理,获取来自故障点的初始电压电流行波波头和由故障点反射的第一个反射波行波波头.以图1为例,线路全长为L,故障点F到M 测量端距离为LM,得到的测距公式:

式中:v为波速;t1为M 侧测量的第一个行波波头到达时间;t2为M 侧测量端的故障点反射的第一个反射波行波波头到达时间.
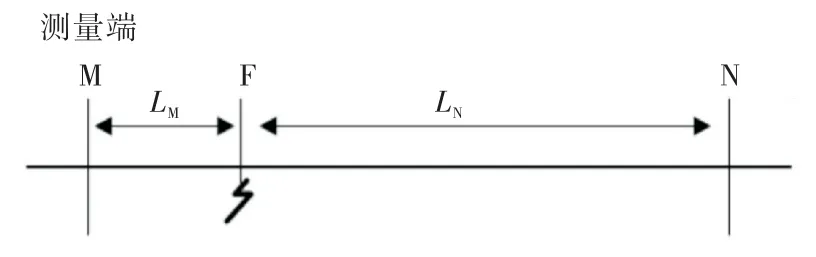
图1 直流输电线路单端测距法示意图
当故障过渡电阻较大时,故障点反射波幅值过小而不易检测,利用初始行波分量与对端母线反射波分量获取的时间差测距可解决此问题.其测距公式为:

式中:Δt为M 侧初始行波分量与对端母线发射波分量获取的时间差.
单端测距算法的难点在于由故障点或者对侧反射的行波的识别困难.其优点是只需要一端的量测,没有时间同步性的问题.
1.2 双端测距法
双端行波测距法需要在线路两端都设置测量点,是通过测量故障点产生的初始行波到达两侧的时间差进行定位,如图2所示.测距公式为:

式中:v为行波波速;t1、t2分别为初始行波到达M测量端和N 测量端的时间;L为线路全长.

图2 直流输电线路双端测距法示意图
为了保证两端时间的同步性,常用的解决方法是测量端的时间采用GPS 授时或者北斗卫星授时系统,但成本较高.双端行波测距法由于两侧只需要检测第一个到达的行波,线路故障点过渡电阻的特性、系统运行方式的变化,以及分布参数对测距复杂性影响较小.因此,双端行波法比单端行波法在线路故障定位中更可靠.本文采用双端法对高压输电系统的线路故障进行测距.
2 CEEMD原理
CEEMD 分解法是在EMD 和EEMD 的基础上改进的方法.在对原始信号进行传统EMD 分解的过程中,它对分解分量添加成对大小相同、符号相反的高斯白噪声,不仅解决了EMD 法分解分量过平滑和模态混叠的问题,而且大大减少了EEMD 法分解过程中产生的噪声残留,最终使得原始信号的分解分量更能反应出奇异信息.它与EEMD 法同是一种噪声辅助方法,其分解步骤如下.
首先,使用不同的噪声添加原始信号中,通过EMD 重复分解过程I次,计算第一阶段的总体平均值FIM1,其表达式如下:

式中:E1为第1个模态给定的算子;x为原始信号;ε0为原始信噪比;wi为权重因子.
然后,计算一阶残差:

继续分解r1+ε1wi,其中ε1为第一阶段选择的信噪比;wi为权重因子,i=1,2,3,…,I,计算第二阶段的总体平均值FIM2,其表达式如下:
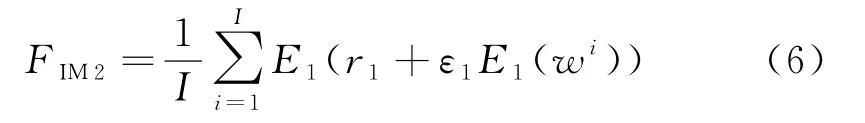
对k=2,…,K,计算k阶残差:rk=rk-1-FIMk,然后提取rk+εkEk(wi)的FIM1分量,其中εk为第k阶段选择的信噪比;Ek为第k个模态给定的算子;wi为权重因子,i=1,2,3,…,I,并计算他们的总体平均值,从而得到目标信号的FIMk+1:

继续此过程筛选,直到残差不能再被分解为止(残差的极值点最后不超过两个),得到最终的残余:
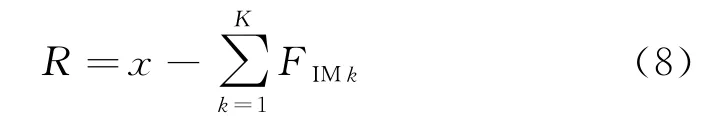
式中:K是FIM的总数.因此,目标信号x可表达为:

3 基于CEEMD的行波测距
HVDC系统发生线路故障,故障点产生向线路两侧传输的故障行波.故障行波由一系列复杂的暂态分量和稳态分量相互叠加而成,具有强烈的非线性、非平稳性.当故障行波传播到线路两侧的监测装置时,监测装置会监测到电气量高频突变的过程.这个突变点时间的获取,可以解析出故障发生点离线路监测点的距离,从而实现故障定位.但是,通过一般方法很难并准确地从监测录波中得到突变点的时间信息.常用的处理方法是利用EMD 的方法分解成一系列的FIM分量,获取其中第一阶FIM分量的行波波头来识别突变点,达到故障定位的目的.本文通过CEEMD 方法来获取故障点的距离并与传统的EMD方法进行对比分析.
故障行波的波头在时频图表现为高频突变,故障行波的波头到达监测装置的时间可以认为是监测录波高频突变的时间点.通过CEEMD 法分解,故障信号中最小特征时间尺度的FIM分量首先被分解出来,即频率最高的FIM分量,此分量相比于其他分量包含着更丰富的高频成分和易于识别的高频突变点.所以,故障行波分量的第一阶FIM分量的第一个高频突变点就是行波波头到达监测点的时间点,通过研究分析第一阶的时频特征可易于解析故障的故障信息.由于HVDC线路发生故障,故障点离监测点的距离越远,高频突变的时间点越容易识别,通过同时利用线路两端的监测功能,避免某一端因为故障点离得太近而识别不出高频突变点.
基于CEEMD 法的故障测距法与传统的EMD法的步骤一致:1)对线路两端的监测装置采集的电压行波信号进行改进EMD 分解,得到前几阶FIM分量;2)对第一阶FIM分量求导并取模值;3)查找模最大值对应的时刻就是FIM分量高频突变的时间点.具体流程图如图3所示.

图3 基于CEEEMD 的故障测距流程图
3.1 故障行波的提取
高压直流输电线路发生故障后,由故障点产生沿着线路两侧传播的电压行波,电压行波在线路与系统之间、线路与故障点之间折反射,其幅值衰减迅速.在故障发生10ms后,换流站控制系统开始启动并作用,控制系统产生的谐波也会影响行波的波形.但是,行波的第一个波头幅值不大易于检测,存在时间短暂,可利用监测装置高速测量故障电压并解析出第一个波头位置.
在线路两侧的监测装置上测量的是线路电压.当线路发生故障后,根据叠加定理,故障线路电压可视为正常分量和故障分量的叠加.同样的,故障行波等同于故障分量,通过采集正常运行的线路电压与故障后的线路电压,两者着差得到故障行波波形.设置输电线路500km 处在第0.5s发生接地故障,故障持续时间0.1s,两侧测量的故障电压如图4所示.正常运行情况下的测量电压如图5所示,计算获得的电压行波如图6所示.

图4 故障时线路两侧测量电压

图5 正常运行时线路两侧测量电压
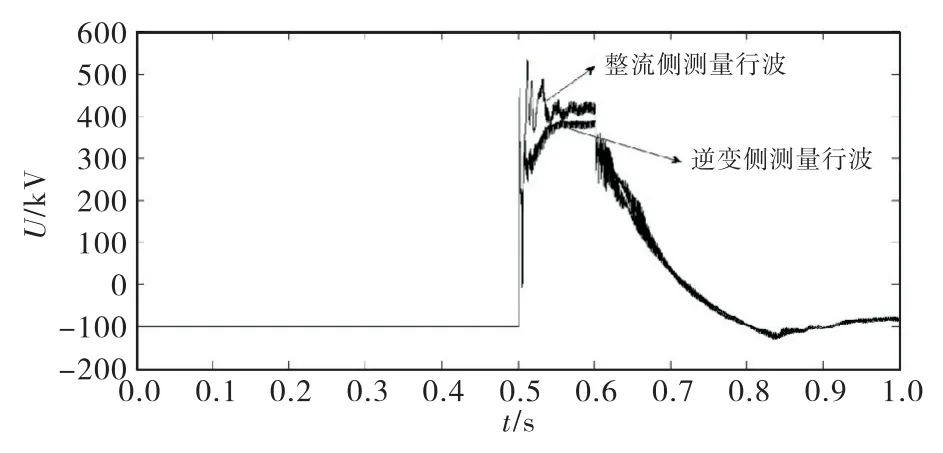
图6 线路两侧得到的故障电压行波
考虑到控制系统的影响,从图6 中截取故障后10ms时间窗的故障行波进行分析,即选用0.5s到0.51s的时间段的波形,如图7~8所示.

图7 整流侧采集的10ms时间窗的电压行波

图8 逆变侧采集的10ms时间窗的电压行波
3.2 故障行波的CEEMD分解
为了对比EMD 法、EEMD 法、CEEMD 法对原始信号的分解效果的影响,对图5所示的电压行波分别进行分解,得到这3类方法的各个分量的分解结果图,分别如图9~11所示.分解分量的前几阶FIM分量最能反映故障特征,故仅取前四阶FIM分量的波形进行显示,图中分量从上到下依次为FIM1到FIM4.

图9 故障电压行波的EMD 分解

图10 故障电压行波的EEMD 分解
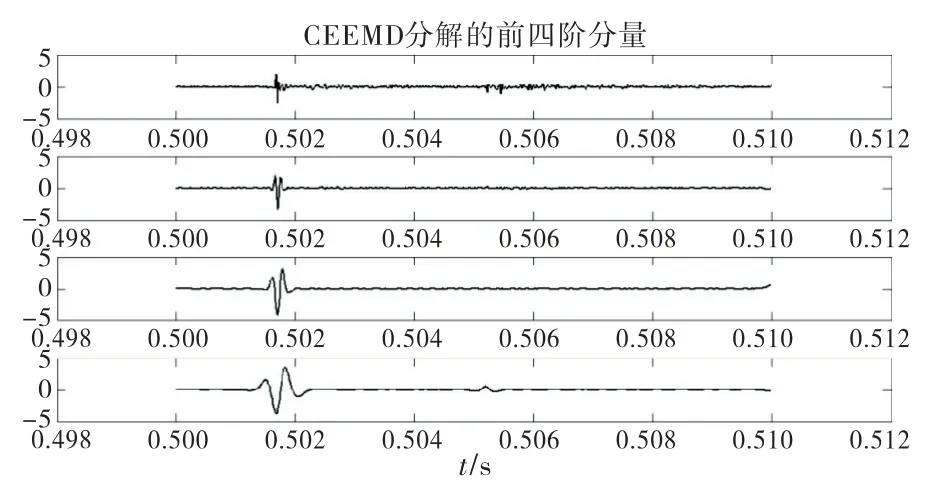
图11 故障电压行波的CEEMD 分解
综合对比图9~11,可以知道EMD 分解后的FIM分量过于平滑,反映不出暂态高频分量;EEMD方法分解后FIM分量包含了很多高频波动,但是FIM1和FIM2没有反映出故障发生时刻的奇异点;CEEMD 方法分解后的FIM分量不仅包含了故障后产生很多的高频成分,而且出现了容易辨识的时间奇异点,而这个奇异点是辨识故障信息的关键.由图11可以观测到第一个FIM的时间奇异点出现在t=0.5017s附近.具体是那个时间点还需做进一步辨识.
3.3 行波波头时间的提取
行波的第一个波头幅值大,为了精确寻找波头到达监测点的时间点,利用Hilbert变换的方法得到波形的时间-Hilbert幅值图像,然后通过寻找最大值点函数来寻找幅度最大值点对应的时间点.对图11所示的FIM1分量进行Hilbert变换得到时间-Hilbert幅值分布图(如图12所示),幅值最大点对应的时间t=0.50172s.依据上述方法得到图8中逆变侧行波的FIM1分量的幅值最大点对应的时间点为t=0.50173s.最后,利用双端测距公式,得到线路故障点的距离.
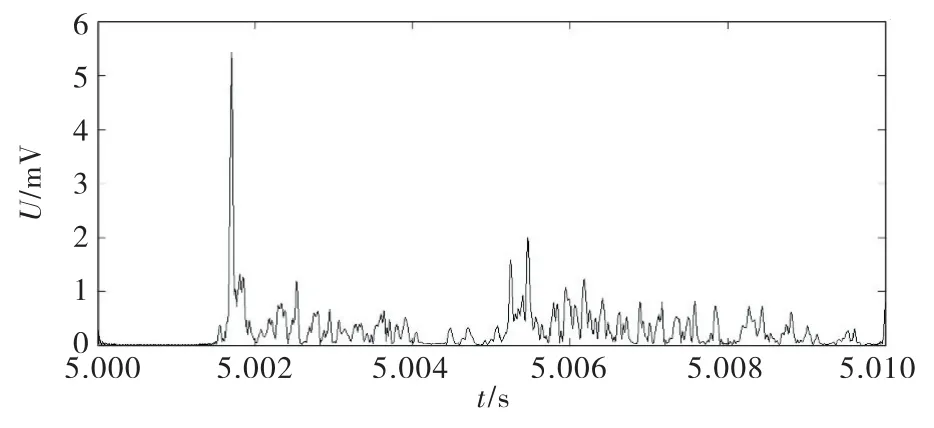
图12 FIM1 的时间-Hilbert幅度谱
4 算例分析
为保证仿真的可重复性,利用PACAD/E-MTDC电磁暂态仿真软件建立GIGRE 提出的HVDC 的标准模型,如图13所示.模型采用单极12脉的方式,直流线路全长1000km,直流额定电压等级为500kV,额定输送功率1000MW.直流输电线路采用架空线结构,其参数为:r=0.03206Ω/km,L=2.2362mH/km,C=0.01001μF/km.
设置3种线路区间内仿真故障类型,考虑到仿真系统启动HVDC的暂态过程,故障发生时间设置不宜过小,设置故障发生时间为0.5s,故障持续时间约0.1s,数据采样频率为500kHz.故障类型见表1.
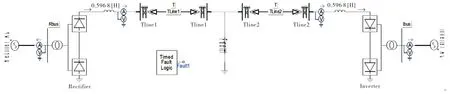
图13 HVDC仿真模型图
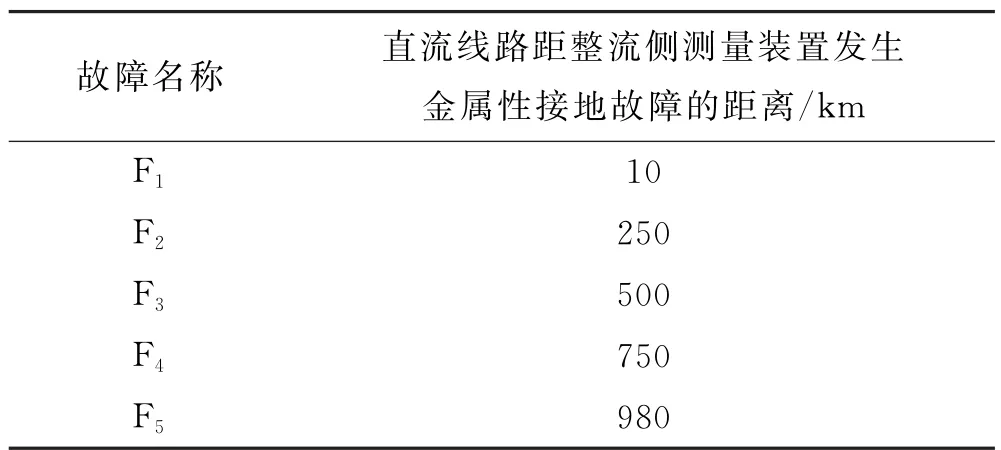
表1 线路的F1、F2、F3、F4、F5 故障的类型
通过PSCAD/EMTDC进行模型仿真,线路两端监测装置对上述5种线路故障后的电压分别进行测量.在Matlab中对仿真数据进行CEEMD 分解得到第一阶FIM,进一步进行Hilbert变换得到故障电压行波的波头到达时间点.根据双端测距公式(3)得到线路故障点位置,统计结果见表2.

表2 线路的F1、F2、F3、F4、F5 故障的测距结果
由表2可以看出,运用CEEMD 方法测量5种线路故障距离,除F1外,其它4种线路故障距离的误差均小于0.5%,能够满足工程应有的要求,有一定的应用价值.
考虑到不同过渡电阻对测距方案的影响,对HVDC线路不同故障F2、F3、F4下进行仿真,故障点过渡电阻分别采用500、800、1000Ω,仿真及其计算结果见表3.
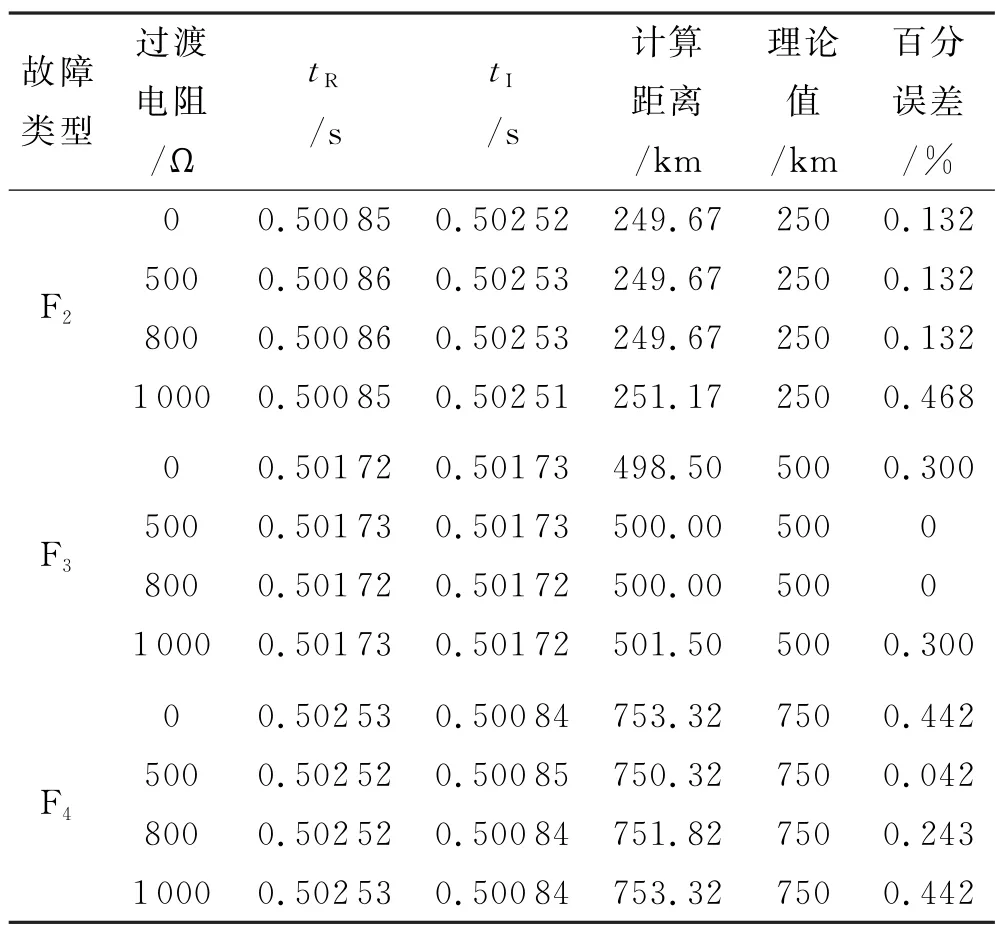
表3 F2、F3、F4 故障在不同过渡电阻下故障测距结果
从表3可以看出,同一个故障点存在不同阻值的过渡电阻时,故障测量距离之间相差很小,均在可接受的范围.
5 结语
针对经验模态分解法存在着分解分量过于平滑和集合经验模态分解法分解分量的噪声分量残余过大的问题,本文利用CEEMD 的方法分解故障行波信号,避免了分解模态分量的过平滑、噪声残余问题,使得其中高频分解模态分量更能反映出高压直流输电线路故障信息.利用PSCAD/EMTDC电磁暂态仿真软件建立HVDC系统标准的GIGRE模型仿真,得到故障线路点不同距离发生故障的暂态电压的仿真波形和数据.采取双端测距法获取线路故障发生位置.仿真结果表明,该方法线路故障测距精度高、受过渡电阻的影响较小.
