例说发散思维在数学解题中的应用

姚志雄

(邵阳市第一中学 湖南邵阳 422000)

经常会听到这样的说法，数学本质上是一门思维学科，学习数学的目的就是用数学的观点去分析思考问题。思维是什么？简单说思维就是思考问题的方法。数学思维也就是人们通常所指的数学思维能力，即能够用数学的观点去思考问题和解决问题的能力。一个人的思维方式决定着其行为方式，若能对自己的思维方式进行一定的评估和分析，将自己思考的过程放大，就能看到很多曾经没有发现的东西，从而在原有基础上有所改变和提高。从数学思想方法层面看，数学思维包含抽象、推理、建模等方面。所谓抽象就是从众多事物中抽取出共同的、本质的属性而舍弃个别的、非本质属性的思维过程。有时也指“抽象的产物（结果）”或“抽象的方法”。具备抽象思维，意味着具备提取主要因素与透过现象看本质的能力。所谓推理，就是指数学和其他理科不同，物理、化学、生物主要依赖实验来进行验证，只有数学可以仅依靠推理得到正确的结果。因此，推理能力意味着突破“眼见为实”的限制。而建模意味着将抽象的规律用数学的语言表示出来，从而可以用数学的方法处理问题。如何培养数学思维？学者们见仁见智，没有一个统一的答案。但有一点可以肯定，就是认为发散思维在数学学习中有着极其重要的作用。发散思维是打破常规，寻求变异的思维，它不受传统束缚，不受思维定势，是创新思维的核心，与创造力有直接关系。

本文着重通过一道不等式问题，探讨一下发散思维在数学学习中的应用。

有些数学问题，常规方法无法解决，这时通过构造辅助函数解题，就能化难为易，迎刃而解。构造辅助函数解题不仅能减少计算量，使原本复杂的问题变得简单，而且对于培养学生分析问题、解决问题的思维能力很有帮助；难点在于它的灵活性及创造性，这也正是数学的魅力。构造函数解题，广泛运用在不等式问题中，在数列、三角函数、方程根的存在性问题中也有涉及。文献[1]总结了几种常见的证明方法：特征分析构造法、和差构造法、积商构造法、局部构造法、变参分离构造法和换元构造法。文献[2]提出了利用作差法、积商法等方法构造辅助函数，再运用其导数来解决数学问题中的不等式问题。文献[3]认为可通过移项法，倒退法和微分方程法构造辅助函数求解不等式。还有很多数学爱好者对构造法进行了探索，他们得到了一些有趣的结论，对丰富不等式的解题方法有积极的推动作用。通过一个具体例子加以说明。

例：已知x2+y2=8，求证：x+y≤4

解法一分析。本题可看成是所求函数f(x，y)=x+y在约束条件x2+y2=8的极值问题，可利用拉格朗日乘数法求函数的极值。

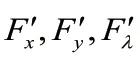
证明：不妨设函数f(x，y)=x+y，构造辅助函数

解得可能极值点为(-2，-2)，(2，2)。

要求一个函数在某种限制条件下的极值的问题，一般可采用拉格朗日乘数法，通过构造辅助函数－拉格朗日函数，再求辅助函数关于各个变量的一阶偏导数，然后令偏导数同时为零，找出可能的极值点，然后进一步计算二阶偏导数在点的值，根据定理加以判断。其实，这个题目有多种方法求解，不妨考虑数形结合的方法。数学是数与形结合的一门学科，借助图形直观分析，能够化繁为简，使题目变得简单容易。

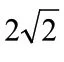
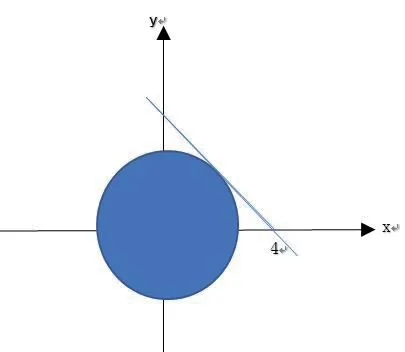
图1 圆与直线相切

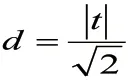
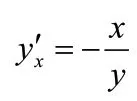
Dweck和她的助手曾经做过一项研究发现[4]，拥有成长型思维的学生在考试中取得前20%成绩的可能性是其他人的3倍；而持有固定型思维模式的学习进入最后20%的可能性是其他学生的4倍。也就是说固定型思维模式的学生，基本都是在班级垫底。说明发散思维在学习过程中十分重要。对于这道题，除了上述两种解法外，还有其他方法。

什么是真正的数学能力？掌握复杂抽象的逻辑推导链条，理解其核心思路的能力，并将其迁移运用至其他数学领域的能力；将不同领域的知识联系、融会贯通的能力；乃至于创造一套理论体系，并运用其解决数学问题的能力等。学习数学不在乎刷题的数量，而在乎刷题的质量，主要是对数学思想方法的掌握。小题大做就是加深对数学思想和方法领悟的一个好方法。我们在遇到一些小题的时候也会有不一样的灵感，感觉从不同途径入手都能解决问题。这往往意味着问题背后有着丰富的背景，这个时候不要放过这灵感，要更加深入地去思考，进行一些探究式的学习。小题大做的目的就在于利用发散思维打通不同知识模块之间的壁垒，又或者完成从特殊到一般的延展。这样主动学习一个小时带来的能力提升可能远远超过一个小时的机械刷题。

我们经常听到，学数学一定要多练习，多训练，达到熟能生巧的地步。但训练也是有讲究的，笔者认为，数学精深训练有九个台阶。第一个台阶是能看懂，就是能够懂得数学定义，定理，公式的来龙去脉。一看到这个定理、公式，脑子里面盘旋的一些问题，一一找到答案。要从内心去回答，找到的答案越多，做出来的问答越多，就懂得越多，这就是能看懂的含义。第二个台阶是能记住。第三个台阶是会解题。看懂是关键一步，做到这一点，马上就迈上了第一个台阶，马上就会跨过第二个、第三个台阶。第四个台阶是熟练解题，在解题过程中不断进行这样的有意识的思维操作的训练，那么熟练解题也为之不远了。第五个台阶是会梳理，每一章都在重复同样的基本结构，把那些知识点都给汇总到这个知识结构里面，就是会梳理。包括每一章都在用什么样的运算技巧，心里面有没有数，这一章用到什么样的运算技巧，能不能1、2、3……这么列出来，一是一、二是二地列出来，如果能这么做了，肯定是会梳理了。第六个台阶是融会贯通，比如函数，是从什么问题引入的，它的严格定义是什么，它对应的几何直观是什么，它具有哪些性质，它与方程、不等式有什么关系，与几何有什么关系，几何问题可否转化成函数问题等，一步步这么做下来，就是融会贯通了。第七个台阶是把握数学思维，所谓数学思维，就是一个一个的基本的思维操作，像各种类型的加、减、乘、除法，像它的定义，为什么会有这样的定义，它的问题是什么，这个定义能解决什么问题，当我们提这些问题，去找它的答案的时候，按照这样的思维去训练的时候，就把握数学思维了。第八个台阶是体验学习的乐趣，虽然学习过程枯燥，费脑费神，但一旦学懂弄通、真正掌握，一股喜悦之情就会油然而生。第九个台阶是能够投入，忘我的学习。达到第八个台阶就很容易到达第九个台阶了，就是乐此不疲，学习三个小时的数学，感觉时间才过了半个小时一样。觉得数学学习不是负担、痛苦、障碍，而是享受、欢乐、成就，解出难题会带来愉悦、乐趣。

要培养学生的发散思维，除了一题多解、举一反三，还要弱化思维定势，进行积极的思维训练、培养学生良好的思维品质。