非公共周期干线协调控制方法1)

王晨宇 成卫 李冰

(昆明理工大学，昆明，650093)

作为城市快速路主要控制手段，干线协调控制主流设计方向有绿波带最大和系统延误最小2种思路。最早由Morgan et al.[1]与Little et al.[2]提出双向绿波信号协调控制的设计方法和MAXBAND模型；随着研究的逐步深入，Gartner et al.[3]针对路段通行能力存在差异，提出了协调控制模型MUTLTIBAND；卢凯等[4]基于经典模型提出了以混合放行模式下的双向干道绿波带宽模型；唐克双等[5]提出了非对称绿波模型，使绿波带控制在交叉口绿灯时间中心位置提高了有效时间；荆彬彬等[6]提出了双周期的干线绿波信号协调控制模型，减少绿灯空放，避免行人过街等待时间过长的现象。梁杰等[7]通过分析车流到达规律，建立了不同周期相邻交叉口间的延误模型。干线系统最小延误优化方法有结合法[8-9]、单目标[10]和多目标的遗传算法[11-13]。目前国内大部分的协调控制研究均在几个交叉口共用同一信号周期的条件下进行优化，然而，该方法在流量波动较大的交通状态下会产生时空资源的浪费。例如，干线系统中某一交叉口流量较小公共周期时间较短，若该交叉口采取半周期控制方案时，交叉口在高峰时段有排队溢出的状况，采取同周期还存在绿灯时间剩余的情况。因此，本研究应对流量相差较大的交叉口实现变周期的协调控制，提出非公共周期的干线协调控制优化模型。首先，推导了干线系统中各交叉口间的约束条件等式；其次，以干线系统延误最小为目标建立非公共周期双层延误模型，并运用动态规划的思想求得变周期交叉口周期时间和相位差；再根据各交叉口流量比修正变周期交叉口绿信比；最后通过交通调查数据验证了模型有效性。

1 非公共周期干线协调控制机理

当采取非公共周期协调控制方案时，系统内存在2种以上的周期时间，即交通流量较大的关键周期和交通流量较小的不定周期，绿波带最大不再是系统最优方式[13]，设定交叉口交通流较大的定周期和交叉口交通流量较小的不定周期。当拟定一个初始相位差后信号周期经过p次循环再次回到初始相位差时为1次循环，记做非公共周期循环(简称非公循环，U)。不定周期会随着每次循环结束后，根据上下游端口流量变化重新计算最佳周期。由于干线系统内周期不相等，当定周期交叉口首个信号周期结束后各交叉口间的相对相位差都会发生变化，所以初始相位差决定了整个干线系统的延误和通行效率[14]。同时非公循环内不定周期的绿信比选取和周期时间变化也将决定干线系统的延误。

1.1 变周期交叉口I2周期时间推导

假设相邻的2个交叉口间距为300～800 m，起始交叉口为关键交叉口。I1交叉口为关键交叉口，I2是变周期交叉口，通过历史流量数据计算关键交叉口的最佳周期为C1，变周期交叉口的最佳周期为C2，为了保证变周期可以根据实时流量的变化而改变其周期时间，非公循环的最大循环时间不超过15 min。

确保非公循环中关键相位的周期循环为整数倍，I2初始周期最小值设置为I1周期时间的一半，将I1半周期时间等分为n份，每一份时间为C1/2n(C1/2n∈[5,30])，根据上下游协调相位的历史流量数据比例选取k份，得到I2交叉口周期时间为C1/2+C1k/2n(k∈[0,n])，I2交叉口协调相位的初始绿信比是定周期交叉口I1的(k+n)/2n倍。当I1、I2周期确定后，关键交叉口I1经过2n/(n-k)-1次循环后相位差恢复到初始相位差，I2周期增长时相应的非公循环次数也会随之增大。I1周期时间为C1，I2周期时间为C1/2+C1k/2n，变周期C2时间取值满足公式

C2=C1(2n+k+nmi)/2n。

(1)

式中：mi取值为0、1、2、…、p。其中p为定周期交叉口与变周期交叉口间的变周期循环次数，p=2n/(n-k)-1。

1.2变周期I3周期时间推导

同理根据关键交叉口与变周期I3协调相位的历史车流量数据的比例选取f份，得到变周期交叉口I3周期取值为C3=C1/2+C1f/2n(f∈[0,n])，f与k取值相互独立，依据上游周期时间和实际车流量。变周期C3时间取值满足公式

C3=C1/2n((n+k)+mi(n+f))。

(2)

式中：mi取值为0、1、2、…、p′。其中p′为变周期交叉口之间非公循环不定周期的循环次数，当C2>C3时，p′=(n+k)/(k-f)；当C2>C3时，p′=(n+f)/(k-f)；当C2=C3时，p′=p。

2 非公共周期最小延误模型

2.1 非公共周期循环延误分析

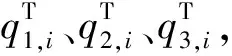
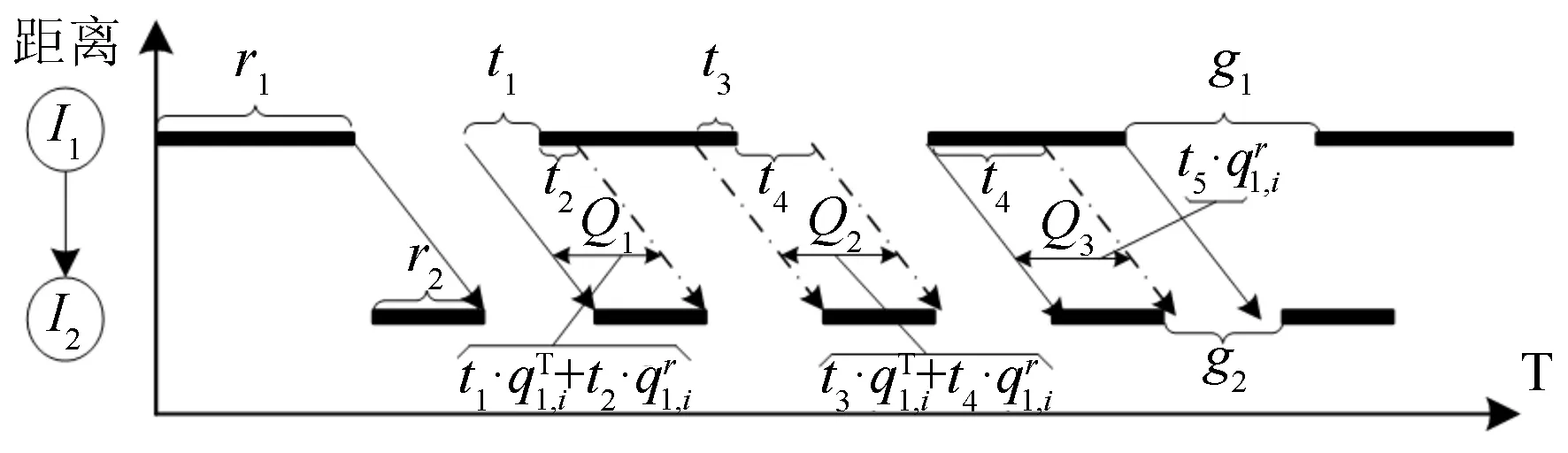
Q1、Q2、Q3分别是下游绿灯亮起时的排队累计量；g1、g2和r1、r2分别为I1与I2交叉口协调相位的绿灯时间和红灯时间。

图1中Q1、Q2、Q3由上游干线流量、支路流量及其相位放行时间决定，每个周期的实际排队累积量不同。下游交叉口单一周期累计量不同，其所需求的最小绿灯时间也不同，在非公循环内每个周期与上游交叉口的相对相位差也不同。所以，当确定了关键周期的信号配时和流量时，非公循环系统的总延误取决于变周期的相位差、周期时间和绿信比。当初始相位差为Δ1,2=l1,2/v1,2，非公循环内其他相位差满足公式

Ψ1=Δ+mi(C2-C1)。

(3)

式中：Ψi是交叉口i协调相位的相位差。

当非公循环内不定周期循环次数为p，p-1次时相邻交叉口的相位差最小，此时的排队累计量最大。引进β变量，

β=mi(Cδ-Cδ+1)。

(4)

式中：mi取值范围为(0,p-1)。

通过调整变量β改变非公循环内每个不定周期与上游交叉口的相对相位差，从而降低干线系统延误。

以Webster延误模型对单车道延误进行计算[16]，基于Webster延误函数，非公循环内3个交叉口的总延误可以表示为

(5)

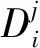
关键交叉口与所有支路交叉口流量稳定时，总延误取决于2个不定周期的延误之和，通过非公循环延误分析得到不定周期延误，取决于初始相位差的选取和2个交叉口的周期时间以及单周期的绿信比。

2.2 基于动态规划的双层延误模型

关键交叉口整体流量相对较大且周期固定，所以从关键交叉口上游到下游方向建立延误模型。首先将模型分为2个层面：定周期与不定周期构建的第1层延误循环，周期的循环次数分别为n次与n+1次；不定周期与不定周期构建的第2层循环，周期分别为n与n′。其中，

(6)

初步设定不定周期干线绿信比是固定的，数值为定周期干线绿灯时间的(k+n)/2n倍。

1)第1层延误模型的构建

在上游流量与支路流量稳定的情况下根据公式(5)，为了求解第1层循环定周期与变周期的最小延误需要将初始相位差和周期时间设为控制变量，基于动态规划思想建模公式为

(7)

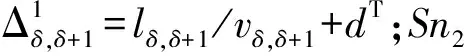
(8)

由于2个交叉口周期不同，非公循环内的p个周期的相对相位差也不相同，其递推公式为

(9)

2)第2层变周期延误模型的构建，根据第1层延误计算思路，可得延误公式为

(10)

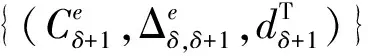
(11)

minD就是使目标函数最小的不定周期交叉口参数集合。上述过程以干线总延误目标函数可以表示为

(12)

3 双向干线协调绿信比优化模型

通过上述延误模型计算得到了非公循环内的不定周期时间和相对初始相位差，此时不定周期干线绿信比是固定的，为定周期干线的(k+n)/2n倍。需要根据实际非公循环每个周期的实际交通流量适当调整绿信比进一步降低干线系统延误[17]。基于Webster绿信比优化模型的改进优化公式为

(13)

式中：gi,p是非公循环内第p个周期的第i相位的绿灯时间；vδ+1,i,p/xi是非公循环内第p个周期的第i相位关键车道流量比；Lδ+1是周期损失时间。

上述延误模型是基于关键交叉口流量进行计算，当计算出不定周期和绿信比时间后就默认了下游方向流量与上游方向相仿，位于端口处的不定周期交叉口，它的下游流向上游方向车流量不取决关键交叉口，此时可能出现2种情况：①支路流量稳定时运行一个非公循环后，位于端口处的不定周期交叉口其下游流向上游方向干道车流量比上游流向下游方向车流量大且不可忽略。②支路流量稳定时运行一个非公循环后，位于端口处的不定周期交叉口其下游流向上游方向流量大于定周期交叉口的上游流向下游方向的车流量。此时需要对不定周期交叉口上下游流量进行判别，公式为

(14)

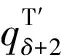
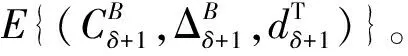
当出现第2种情况时，需要全面对比2个端口的整体流量，重新确定关键交叉口更改模型推导方向。如果2端口处交叉口流量接近，可以将2个交叉口设定为定周期，第1层延误模型计算出集合A、B时，只需调整不定周期与下游定周期交叉口相位差即可，公式为

(15)

此时得到不定周期交叉口与下游定周期交叉口的相位差Δδ+2，将各个交叉口流量带入公式(13)，调整绿信比完成建模。动态规划流程与优化过程见图2。

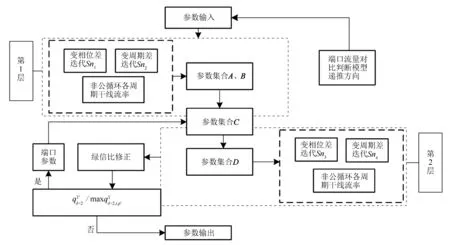
图2 动态规划流程图

4 实例分析

应用上述的非公共周期干线协调控制模型，以云南省曲靖市沾益区的3个交叉口为实例对上述延误模型有效性进行仿真验证，并将制定的非公共周期控制方案与公共周期控制方案进行对比。I1、I2和I3分别为太昌路、海口路和河西路3个交叉口，干道交叉口流量见表1，交叉口示意图如图3所示。

通过流量数据公共周期干线协调控制方法制定配时方案，公共周期控制方案各个交叉口的平均延误等仿真数据见表2。

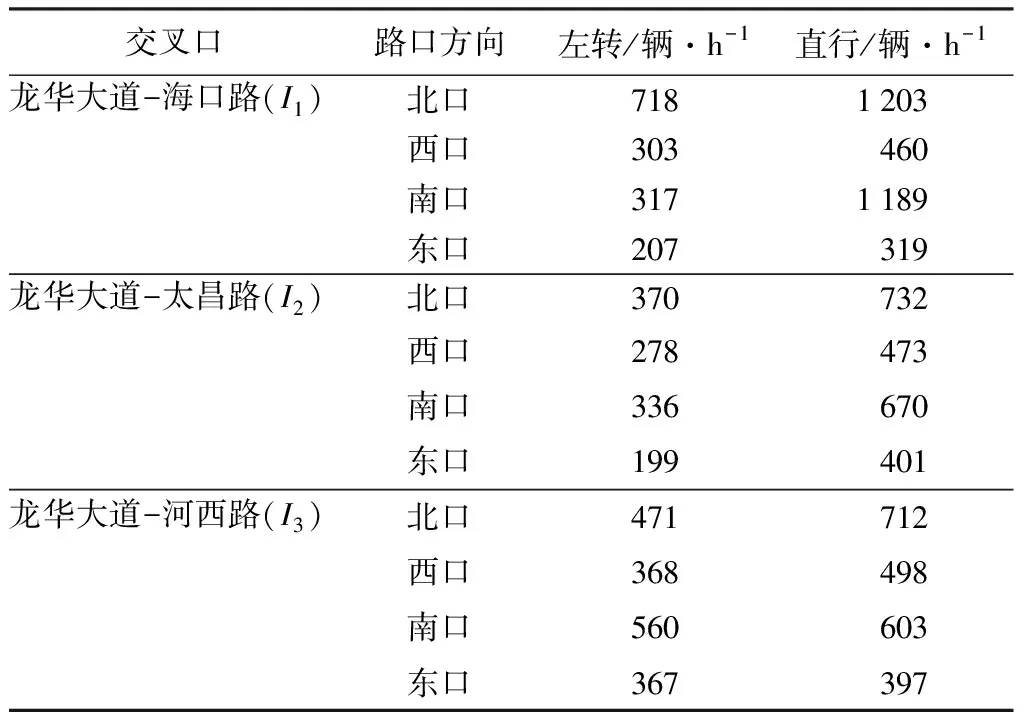
表1 干道交叉口流量

保持相位与关键交叉口的周期时间，利用本研究提出的非公周期最小延误模型对传统干线协调控制方案进行优化，根据关键交叉口周期时间取周期迭代间距为C1k/2n=20。将迭代间距带入第1层延误循环模型得到相位差、周期时间等交通参数集合A，将其带入VISSIM仿真平台得到交叉口延误结果见表3。

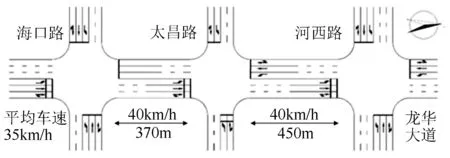
图3 干线交叉口路况

表2 公共周期控制方案

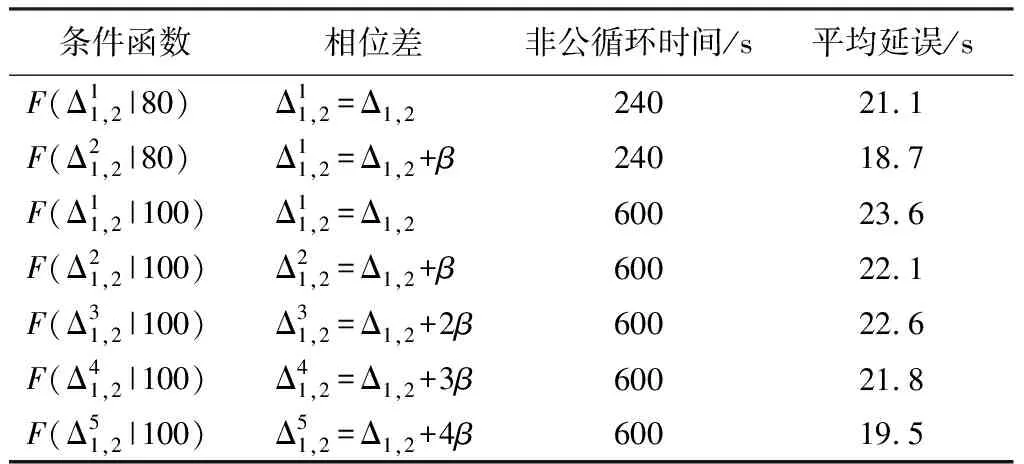
表3 第1层延误模型仿真结果

根据第1层非公循环延误模型的仿真结果，将I2交叉口周期时间设定为80、100 s，根据I2交叉口周期时间取周期迭代间距分别为C1f/2n=20和C1f/2n=30。将2种迭代间距和周期时间带入第2层非公循环延误模型得到相位差、周期时间等交通参数集合C，再将参数输入仿真平台得到结果见表4。

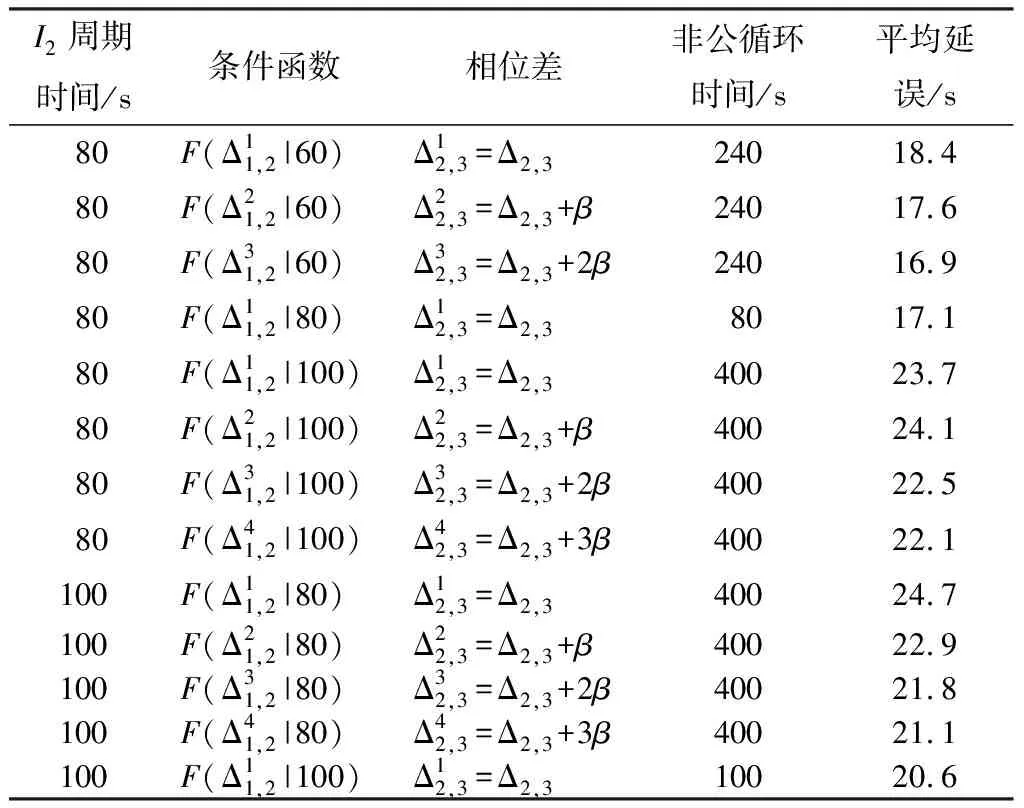
表4 第2层延误仿真结果

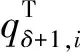
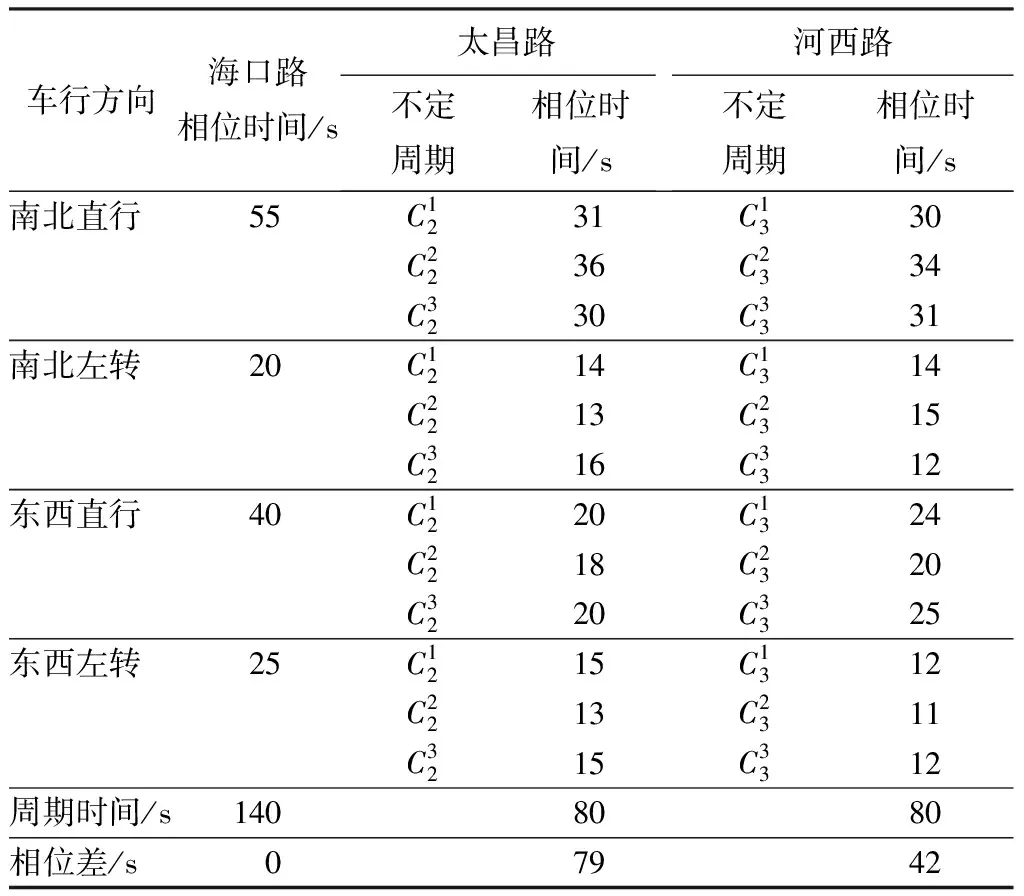
表5 非公共周期控制方案

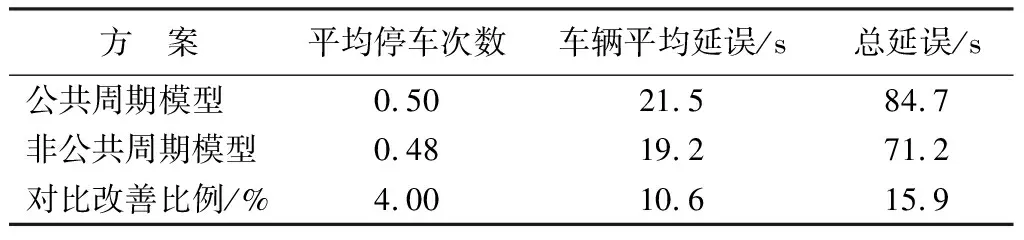
表6 不同方案的结果对比

在道路饱和度为0.7时，通过仿真验证对比2个模型的结果(见表6)可见：与公共周期方案对比，优化了相位差与绿信比后，车辆平均延误降低了10.6%，整个干线系统总延误降低了15.9%，平均停车次数降低了4.0%，平均停车次数优化效果较小，但车辆延误优化显著，尤其总延误优化程度明显，说明了通过调整周期时间不仅降低了干线车辆延误时间，也降低了支路车辆的延误时间。因此本方法可以较好地提高干线系统的通行效率。

5 结束语

本研究首先基于半周期干线协调控制分析了不定周期与公共周期之间的约束关系，突破了公共周期条件的束缚，并以一个非公共周期循环为优化目标，利用动态规划的思想建立了基于Webster模型的双层延误模型，解决了流量较小的交叉口最佳周期与初始相对相位差的选取问题；同时考虑到下游交叉口流量的不确定性，建立了非公共周期干线协调的绿信比修正方案。通过案例分析可知，所建立的非公共周期干线控制优化方案有效降低了车均延误、平均停车次数、干线系统总延误，表明该模型对优化交叉口流量波动较大的干线系统具有重要意义。