基于局部保持投影的鲁棒稀疏子空间学习
2021-05-26胡文涛陈秀宏
胡文涛,陈秀宏
江南大学 数字媒体学院,江苏 无锡214122
在许多实际应用领域,数据的维度往往很高,这时选择合适的低维数据表示显得尤为重要的[1-3]。合适的数据表示可以在有效地降低相应算法复杂性的同时提高后续分类模型的准确性。为此,许多学者提出了子空间算法[4-5]来获得合适的数据表示。子空间学习算法的目的是把高维特征空间投影到低维子空间。
根据是否使用标签,子空间算法可以分为三类:有监督子空间算法、半监督子空间算法和无监督子空间算法。有监督子空间算法通过利用标签信息学习得到有判别性的投影矩阵,例如线性判别分析[6](Linear Discriminant Analysis,LDA)和基于此进行改进的一些方法,如鲁棒稀疏判别分析[7](Robust Sparse Linear Discriminant Analysis,RSLDA)和鲁棒判别分析[8](Robust Linear Discriminant Analysis,RLDA)等。RSLDA 算法对模型施加重构约束,使得投影矩阵保持数据样本的主成分信息,同时利用L2,1范数约束投影矩阵,增加算法的鲁棒性,剔除冗余信息,提高投影矩阵的解释性。半监督子空间方法同时使用带标签的样本和不带标签的样本来提升算法性能。文献[9]提出的半监督判别回归,利用带标签样本使类内离散度最大,并使用无标签样本保持数据样本的内在几何结构。无监督子空间方法通过保持数据几何结构来学习投影矩阵。例如,主成分分析[10](Principal Component Analysis,PCA)将训练样本投影到低维子空间,通过最大化投影方差,达到保持主成分的目的;文献[11]也给出了一些子空间方法的图嵌入统一框架。然而,上述方法包含两个过程:(1)特征学习(数据表示);(2)使用学习得到的投影矩阵进行分类。两个独立的过程不能保证得到算法的全局最优值。文献[12]提出了鲁棒结构子空间算法(Robust Structured Subspace Learning,RSSL),通过结合图像理解(即给图像赋予标签的过程)和特征学习来缩小底层特征和高层语义存在的语义间隙,但该算法没考虑数据样本存在的重构误差。于是,Fang等[13]提出了鲁棒隐式子空间学习算法(Robust Latent Subspace Learning,RLSL),该算法联合考虑隐式子空间问题和分类模型参数求解,但是忽略了数据的局部几何结构。局部几何结构通过构造图矩阵可以表示数据样本的亲和关系,从而剔除离群点的干扰。文献[14]提出了基于局部保持投影(Locality Preserving Projection,LPP)的联合特征选择和子空间学习算法(Joint Feature Selection and Subspace Learning,FSSL),利用L2,1范数行稀疏性质,联合考虑了特征选择和子空间学习,取得了良好的效果。
为了充分利用子空间算法的优点,同时能揭示数据样本的局部几何结构,本文提出一种基于局部保持投影的鲁棒稀疏子空间学习算法(Robust Sparse Subspace Learning Based on Locality Preserving Projections,LPPRSSL)。该算法通过联合考虑子空间学习和分类模型问题,得到更具有判别性的数据表示;通过保持数据的局部结构,减弱离群点的干扰,同时利用L2,1范数获得行稀疏的投影矩阵,从而得到更有鉴别能力的低维特征。最后,设计交替迭代方法来求解以上模型。图1是本文算法框架图,通过投影矩阵Q 得到数据样本的“干净”子空间用于分类模型。在多个数据集上进行实验,验证了该算法的有效性。
1 相关工作
假设给定训练样本矩阵X ∈Rm×n,其中每个列向量xi( i=1,2,…,n )为一个样本,m 为样本的维数,n为训练样本的个数。
1.1 线性回归分类器
线性回归模型[15]通过把数据样本回归到标签空间进行分类,可表示为:

其中,A ∈Rc×m是回归系数矩阵;Y=[ y1,y2,…,yn] ∈Rc×n(c ≥2 是类的数量)是标签矩阵,并定义为:

1.2 基于子空间学习的分类模型
为了得到新的数据样本表示,首先可把样本投影到子空间,即QTX ;再把新的数据样本表示用于分类器f( x,B )的训练阶段。通过最小化分类误差来优化投影矩阵Q,使得到的数据样本表示QTX 与分类过程紧密相关。相应的优化模型表示为:

其中,xi∈Rm是数据样本X 的第i 个样本,B 是回归矩阵,ψ 是惩罚函数。
2 基于局部保持投影的鲁棒稀疏子空间学习
将特征学习和分类过程相结合,并利用数据样本的局部结构,使算法对离群点有较好的鲁棒性,本文考虑如下基于局部保持投影的鲁棒稀疏子空间学习模型:

其中,Q ∈Rm×d表示投影矩阵,B ∈Rc×d表示回归矩阵,d(d <m) 是降维后特征的维数,c 是样本的总类数。目标函数中的第一项是通过最小化分类误差来优化投影矩阵Q,使得学习到的数据表示QTX 与分类过程紧密结合;第二项保持了数据在低维样本空间的局部结构,并使得算法对离群值具有鲁棒性;第三项通过L2,1范数的行稀疏性剔除原始特征空间中的冗余特征,使得提取出来的特征更具有判别性;第四项是描述噪声矩阵的稀疏性,使模型对噪声具有更强的鲁棒性;第五项防止模型过拟合,使其具有较好的泛化能力。第一个约束条件考虑数据样本的重构误差,使学习得到的数据表示QTX 能减少噪声矩阵E 的干扰。对重构矩阵P 进行正交约束,避免式(4)出现平凡解。
模型(4)中目标函数虽然对单个变量是凸的,但对所有变量不是联合的。下面可使用交替方向乘子法[16]来求解。首先,为了使模型(4)可分,引入辅助变量A,模型可以改写为:
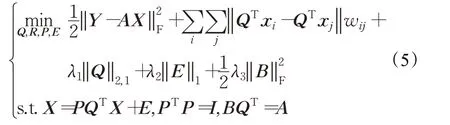
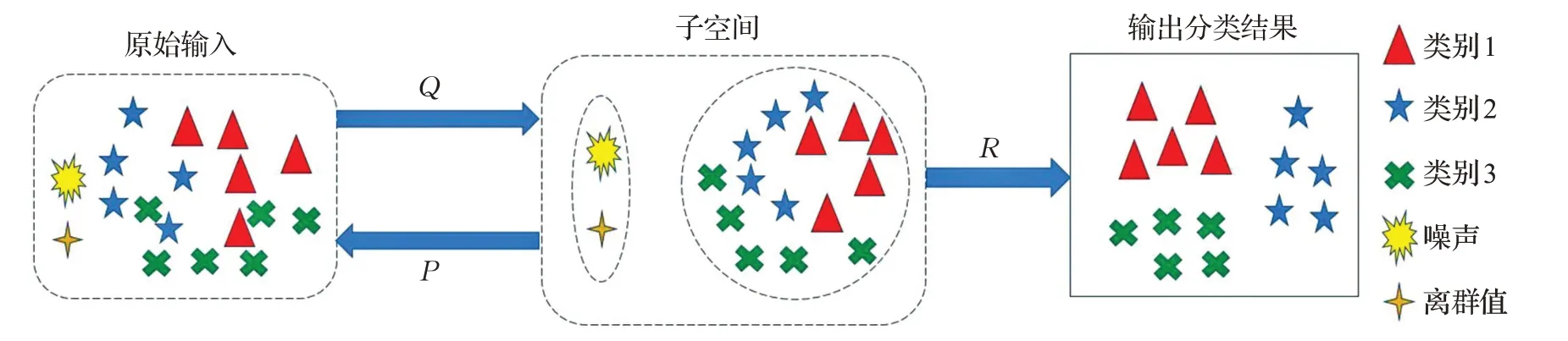
图1 算法框架图
则模型(5)的增广拉格朗日函数为:

其中,C1和C2是拉格朗日乘子矩阵,μ >0 是惩罚参数。使用交替方向乘子法依次求解各变量。
当Q,B,E,P 固定时求A。式(6)可以化为:

关于A 求偏导并令其结果等于0可得:

当Q,B,E,A 固定时求P。可以通过式(9)求解P:

令M=X-E+(C1/μ ),式(9)可以化为:

式(10)是一个典型的正交procrusters问题[17]。对矩阵MXTQ 进行奇异值分解(SVD)可以求得矩阵P ,即SVD( MXTQ )=USVT,P=UVT。
当P,B,E,A 时求Q。式(6)可以化为:

关于Q 求偏导并令结果为0可得:
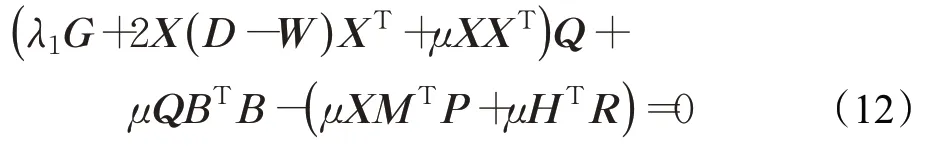
其中,H=A-C2/μ 。式(12)可通过求解Sylvester 方程[18]求得Q。
当P,Q,E,A 固定时求B。式(6)可以化为:

关于B 求偏导并令其等于0可得:

其中,K=A-C2/μ。
当P,Q,B,A 固定时求E:
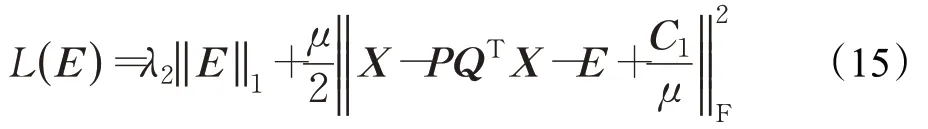
极小化式(15)可通过收缩算子求解:

其中,Shrinkλ2/μ=sign( t )max(| t |-λ2/μ,0 )。
最后,Langrange 乘子矩阵C1、C2和惩罚参数μ 的迭代如下:
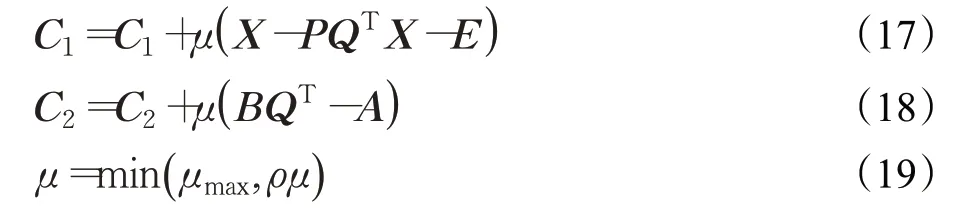
其中,ρ 和μmax都是常数。为了提升算法速度,本文实验首先通过PCA初始化正交矩阵P,而算法终止条件为迭代中最近两次目标函数值插值的绝对值小于0.000 1。综上所述,LPPRSSL算法步骤如下:
输入:数据集X ,维数d,惩罚参数λ1、λ2和λ3。
初始化:通过PCA 初始化正交矩阵P ,A=0;Q=0;B=0;E=0;C1=0;C2=0;μmax=105;ρ=1.01;μ=0.1。
while no convergence do
1. 通过式(8)更新矩阵A;
2. 通过式(10)更新矩阵P;
3. 通过式(12)更新矩阵Q;
4. 通过式(14)更新矩阵B;
5. 通过式(16)更新矩阵E;
6. 通过式(17)、(18)、(19)更新矩阵C1、C2和惩罚参数μ;
end while
输出:转换矩阵A
在得到变换矩阵A 之后,利用A 把测试样本Xtest投影到标签空间得到其预测标签,即j*=arg maxj( AXtest),j=1,2,…,c。
以上算法的复杂度主要集中在求A、P 和Q 上,分别为O( m2c+m3)、O( m2n )和O( m3+2m2n )。因此,本文算法的复杂度为O( ω( m2c+2m3+3m2n )),其中ω 为迭代次数。
3 实验结果与分析
为了验证本文算法LPPRSSL的性能,分别在AR数据集、COIL20数据集和BioID数据集进行实验,并将结果与RSLDA[7]、RLSL[13]、LPP[14]及线性回归分类器(Linear Regression Classification,LRC)等算法进行比较。实验的硬件环境为Windows 10,Intel Core i5 3.3 GHz CPU,内存为8 GB,编程软件为Μatlab 2016a。
3.1 数据集
AR人脸数据集包含126人的4 000多幅人脸图像,它们分别是在不同光照、表情和部分遮挡情况下采集的。实验时选取20人,每人26幅图像,每幅图像的大小为32×32,对所有样本分别加入大小为10×10 和15×15的遮挡。
COIL20 数据集是哥伦比亚物体图像库中的数据集,包括20 个个体的彩色图像,每个个体具有72 幅图像,每个图像以5°的姿态间隔拍摄。实验中选择20 个物体每个72 幅图像共720 幅图像。对所有样本加入密度为0.1和0.2的椒盐噪声。
BioID人脸数据集包含来自23个测试人员的1 521幅灰度图像,这些图像分别是在不同的光照、姿态和表情变化情况下采集的。实验使用了其中22 个人的图像,每人25张,共550张。对所有样本加入密度为0.1和0.2的椒盐噪声。
图2为样本部分物体图像及加噪图像。
3.2 实验结果分析
图3展示了在AR(10×10遮挡)、COIL20(0.2密度椒盐噪声)和BioID(0.2密度椒盐噪声)这三个数据集上数据样本之间的相关性(Z 轴为相关性,X、Y 轴为样本数)。从图(b)和图(c)中可以看出,COIL20 和BioID 数据集样本之间比较离散,在学习子空间时更可能受到离群值的干扰,本文算法通过局部结构可以在一定程度上剔除离群点的干扰,从而提高算法的识别效率,这也在下面的实验当中得到验证。
本节研究特征维数和样本数对实验的影响。图4分别给出了在不同数据集上各个算法识别率与子空间维数的关系。在含噪AR 数据集上每类训练样本数为10 个,含噪COIL20 数据集和含噪BioID 数据集上每类训练样本数为20 个,其余图像作为测试样本。子空间维数分别从10 维开始,每隔10 维取值,直到200 维(在COIL20数据集上到180维)。
从图4中可以看出,本文算法LPPRSSL平均识别率均高于其他比较算法(LRC 算法并未降维,故在图4 中未展示其在低维的识别结果),这是因为本文算法通过最小化重构误差和回归损失,提取出干净的数据表示QTX 用于分类模型,以提取更具有判别性的特征;同时在模型中使用L2,1范数稀疏特征子空间,剔除了冗余特征。另一方面,LPPRSSL 算法在保持数据样本局部几何结构的同时降低了异常值或噪声的干扰,保留了降维后数据样本的内在结构,使算法能更加准确地恢复数据的内在流形结构,提高了识别效果。此外图5给出了目标函数的收敛图。从图中可以看出,在三个数据集上都能快速到达收敛,这说明了算法模型具有较好的收敛性。

图2 数据集的部分原始图像及加噪图像

图3 各数据集之间的样本相关性

图4 各算法在不同数据集上识别率与子空间维度的关系图

图5 目标函数收敛图

表1 各个算法在不同样本数下的平均识别率
表1 是在三个含噪数据集上不同样本数下识别率的比较,子空间维度分别为200、180和200。从表1中可以看出随着训练样本数的增加,所有算法平均识别率都不同程度地增加,但本文算法识别率要高于其他对比算法。LPPRSSL 算法比RLSL 算法识别率高,这是因为LPPRSSL 算法保留了数据的局部关系,剔除了异常值的干扰,并且通过L2,1范数提取了主要特征;LPPRSSL算法比RSLDA算法高,是因为LPPRSSL算法考虑了标签信息,可以提取更具有判别性的特征。LRC 算法和LPP算法比本文算法低,是因为没有联合地考虑子空间问题和分类问题,导致得到的投影矩阵不是全局最优值。
表2给出了在AR(10×10遮挡)、COIL20(0.1密度椒盐噪声)和BioID(0.1密度椒盐噪声)这三个数据集上不同算法的特征冗余度(RED)。特征冗余度公式如式(22)所示,F 表示特征子空间,XF表示由特征子空间F 表示的数据样本,corri,j表示特征子空间F 中特征si和特征sj关联系数,关联系数通过XF计算。特征冗余度越小,说明算法性能越好[19]。从表2中可以看出,LPPRSSL特征冗余度是最小的,因此本文算法能取得比其他算法更好的效果。
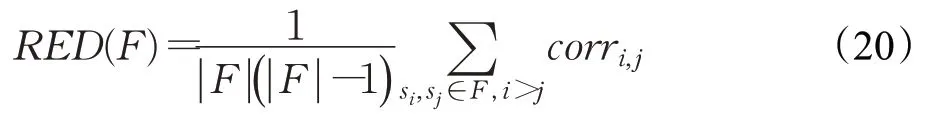

表2 在不同数据集上的特征冗余度
3.3 参数分析
本节研究正则化参数λ1、λ2和λ3对LPPRSSL 算法识别率的影响,分别在10×10 黑色遮挡的AR 人脸数据集、椒盐噪声密度为0.2的JAFFE数据集和椒盐度为0.1的COIL20数据集上进行实验,每个数据集分别选取10、10和20张图片作为训练样本,其余的图像作为测试样本。

图6 正则化参数与平均识别率的关系图
图6 是在三个含噪数据集上正则参数和平均识别率的关系。 λ3控制着算法的泛化能力,本文取值为0.01。对正则化参数λ1和λ2在[0.000 01,100]取值。由图6可知,当λ1在[0.001,1]和λ2在[0.01,1]取值时,算法的识别效果达到最佳。另外,由该图还能看出,正则化参数λ2(控制着噪声的稀疏程度)在[0.01,1]的大多数值都能取得比较好的识别效果,这也说明了本文算法具有比较好的鲁棒性。
4 结束语
本文提出了基于局部保持投影的鲁棒稀疏子空间学习算法,并获得了合适的数据表示。该算法通过最小化重构误差和回归误差来得到最优投影矩阵,同时通过保持数据的局部结构,减少异常值的影响。在不同的数据集上实验表明,该算法具有较好的鲁棒性和识别性能。但是算法复杂度相对较高,如何降低算法在实际应用中的复杂度有待于进一步研究。
