长距离输水管渠结合系统闸阀联合调控方式研究

王浩骅，管光华，饶柏京，崔恒富，陈 刚，顾世祥

（1.武汉大学水资源与水电工程科学国家重点实验室，武汉430072；2.广东省水利电力勘测设计研究院有限公司，广州510635；3.云南省水利水电勘测设计研究院，昆明650021）

0 引 言

为缓解水资源短缺，我国建立了许多大型调水工程，由于其调水距离长、输水流量大、调控过程十分复杂，输水形式也是因地而异，而渠道与管道连接是长距离调水工程中最常见的跨越沟谷地形的输水形式。目前国内外有许多这类调水工程，比如韩江粤东灌区、引黄济青工程[1]、东深供水工程[2]等。由于管道的弹性波波速与明渠重力波波速有着数量级的差异，管道和渠道联合调控的响应特性也是相差巨大，两者的控制往往难以同步。本位旨在探索闸阀联合调控方式，以期提高调水工程的运行效率，为管理者提供合理的运行方案。这也有利于保障灌区的节水灌溉，实现灌区和输配水系统的安全、高效及自动化运行。目前，国内外对于管渠系统的模拟仿真及调控研究成果十分丰富。国外方面，Meryerpeter等[3]以尾水隧洞为研究对象，针对调压室放空与充满以及对水轮机展开各项操作下的场景展开了较为详细的研究以及分析，从此开启了对明满流的分析以及探究。Wiggert[4]将普莱斯曼(Preissmann)窄缝以及移动界面等引入激波拟合方法，对明满流展开了针对性的研究，使普莱斯曼窄缝法的应用得到了拓宽。Cunge 等[5]于1964年针对封闭的管道，在其顶端引入假定的开口狭槽，将其转为明渠流的问题，使得管道和明渠的计算方法得到统一。国内方面，李辉等[6]使用特征隐式格式以及相应的数学方程组，借助狭缝技巧将管道划分为管道流以及明渠流，简化了明满流的计算。杨开林等[7]以有压管以及明渠为对象，针对其内部的水力瞬变情况，将狭缝处理方法引入其中，获得了较好的模拟结果。刘梅清等[8]以大型泵站为对象，针对其内部的复杂抽水系统，将特征线求解格式引入其中，并取得了理想的结果。万五一[9]在普莱斯曼窄缝法的基础上提出了变步长增量法，建立了管渠组合系统的非恒定流同步计算模型，为管渠组合系统提供了新的计算方法。但是由于管渠结合系统的响应特性差异性巨大，现有研究成果中并未见对闸阀联合调控的控制逻辑差异和调控方式的研究。本文采用数值模拟的方法，在处理一维明满流数值计算时采用窄缝法将有压流控制方程与明流控制方程统一，选择管渠结合系统的前馈逻辑与反馈算法中的PI 增益系数与动作频率几个要素进行研究对比，寻找闸阀联合调控中的异同点，为提出合理的闸阀联合调控方式奠定基础。本文旨在探索管渠结合系统中的闸阀联合调控方式，寻求闸门和阀门不同的控制逻辑和控制差异，为实际工程中管道和渠道结合的系统提供参考。

1 管渠一维非恒定流及PID控制

1.1 明渠一维非恒定流模型

圣维南方程组由反映质量守恒定律的连续性方程和反映动量守恒定律的运动方程组成[10]。

（1）连续性方程。根据质量守恒，流体系统的质量随时间的变化率为零，并运用输出方程，并考虑旁侧入流，则一维明渠非恒定渐变流的连续性微分方程通常可以表示如下：

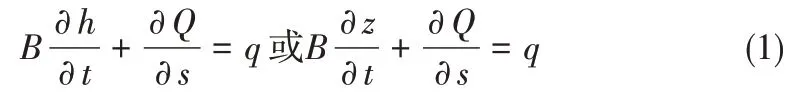
（2）运动方程。对于明渠的非恒定渐变流，z通常取在水面，水面相对压强p为0，考虑到流量和流速的关系Q=v A，一维明渠非恒定渐变流的运动微分方程可以表示如下：

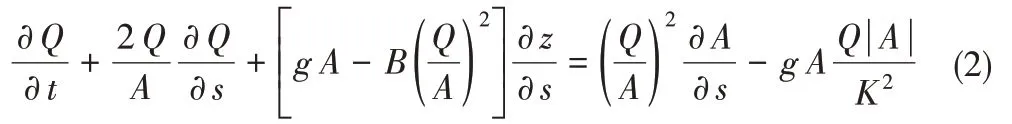
式中：B为水面宽，m；z为水位，m；t为时间，s；Q为流量，m3/s；s为断面的距离坐标，m；g为重力加速度，m/s2；A为过水断面面积，m2；v为水流沿轴线方向的流速，m/s；h为水深，m；q为旁侧入流量，m2/s。

1.2 普莱斯曼窄缝法

在实际输配水工程中，若水流为明渠流动，可以应用明渠一维非恒定流的控制方程求解；若水流为有压流动，可以应用有压管道一维非恒定流的控制方程求解；若水流同时通过管道和渠道时，需要一种统一有压流和无压流的方法来求解。鉴于此，1961年普莱斯曼提出了窄缝法这一经典思想，此后，国内外学者对于这方面的研究大多基于该思想。

首先，为了比较明渠一维非恒定流和有压管道一维非恒定流的基本方程的差别，现将两组基本方程展示如下。明渠一维非恒定流的基本方程：

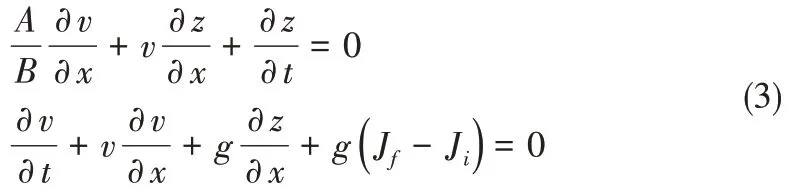
有压管道一维非恒定流的基本方程：

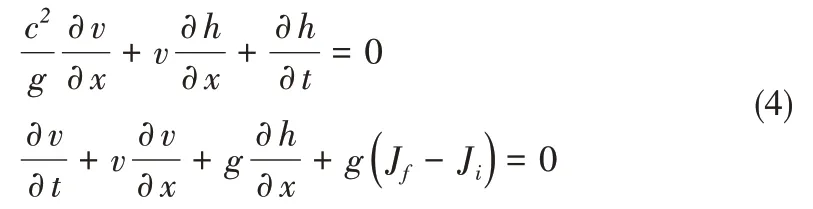
式中：c为水击波速，m/s；J为水力坡度。

其次，从明渠流的基本方程和有压流的基本方程比较中，可以看出，如果将有压管道一维非恒定流的基本方程中的压强水头h看做是明渠基本方程中的水深y，且有压流水击波速c那么，明渠一维非恒定流的基本方程和有压管道一维非恒定流的基本方程在形式上就完全统一了。

最后，值得注意的是，水流在有压流动时，水面宽度B=0，这样连续方程已经失去意义。为了使两组方程计算统一起来，假设在有压时，管道顶上面有一个假想的窄缝，窄缝的宽度为B=g A/c2。该窄缝对湿周、过水断面面积、流速以及压强等均无影响，这种方法就称作普莱斯曼窄缝法。

1.3 有限差分法

有限差分法是求解圣维南方程组常用的数值计算方法之一。有限差分法又可分为显式差分法和隐式差分法，隐式差分法的基本思想是直接求解由内断面方程和边界方程联立组成的方程组。在所有隐式差分算法中，应用较多的是四点偏心格式[11]。由于其计算效率较高，并且无条件稳定的特定，一直被人们沿用至今。四点偏心格式，也称普莱斯曼差分格式，是针对矩形网格中间某点M将因变量的微分形式转化为差分形式。在距离步长上M点处于正中心，而在时间步长上，存在一个权重因子θ，偏向已知时层为θ，偏向未知时层为1-θ，见图1。

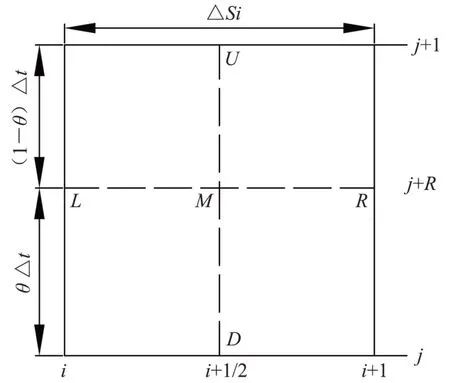
图1 四点偏心格式的网格Fig.1 Preissmann difference format grid

U、D、L、R四点的流量可以通过线性差值得到，由此可以得到M点流量和水位的差分形式，并代入圣维南方程组，可以得到圣维南方程组的差分方程：

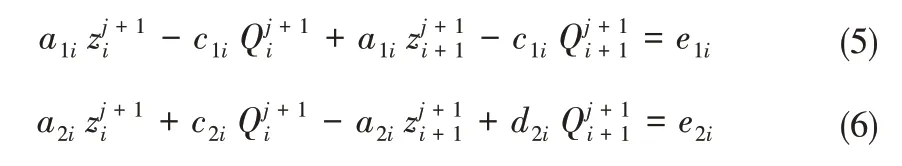
式中：i=1，2，…，N-1；z为水位，m；Q为流量，m3/s；a、c、d均为数值方程的系数。

1.4 PID控制

PID 控制器[12]同时具有比例、积分和微分3 种控制作用，也可以只用一项或两项组成，如P 控制器、PI 控制器、PD 控制器，它们统称为PID类控制器。比例控制用来使过程较快地稳定，积分控制减小或消除静差，微分控制克服受控对象的延迟和惯性，加快系统的动作速度，缩短调节时间。为避免水位波动对控制造成影响，渠道输水控制中较少采用微分控制，因此本文采用PI 控制器，取Kp=10，Ki=0.6。PID 控制方程如下：

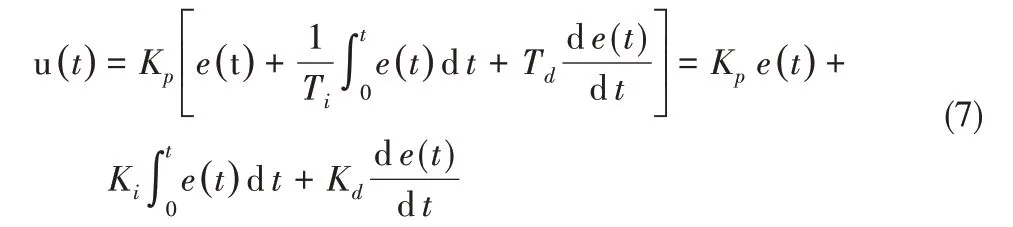
式中：Kp为比例系数，Ti为积分时间常数，Td为微分时间常数；Ki=Kp/Ti，为积分系数；Kd=Kp Td，为微分系数。

PID 控制器各校正环节的作用如下：①比例环节：即时成比例地反映控制系统的偏差信号e(t)，偏差一旦产生，控制器立即产生控制作用以减小误差。当偏差e=0时，控制作用也为0。因此，比例控制是基于偏差进行调节的，即有差调节。②积分环节：能对误差进行记忆，主要用于消除静差，提高系统的无差度，积分作用的强弱取决于积分时间常数Ti，Ti越大，积分作用越弱，反之则越强。③微分环节：能反映偏差信号的变化趋势(变化速率)，并能在偏差信号值变得太大之前，在系统中引入一个有效的早期修正信号，从而加快系统的动作速度，减小调节时间。

从时间的角度讲，比例作用是针对系统当前误差进行控制，积分作用则针对系统误差的历史，而微分作用则反映了系统误差的变化趋势，这三者的组合是“过去、现在、未来”的完美结合。

2 研究方法

2.1 仿真流程

本文在武汉大学研发的输水渠道系统运行仿真与控制软件[13]基础上进行二次开发，对目标渠道进行仿真，仿真的逻辑框图如图2所示。

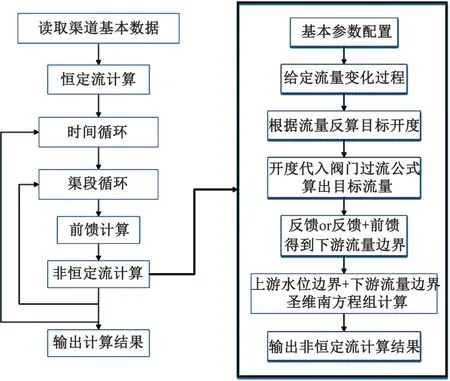
图2 仿真程序框图Fig.2 Block diagram

2.2 控制要素

为更好的表现闸门和阀门在调控中的差异性，本文选择管渠结合系统的前馈逻辑与反馈算法中的PI 增益系数与动作频率几个要素进行研究对比，见表1。

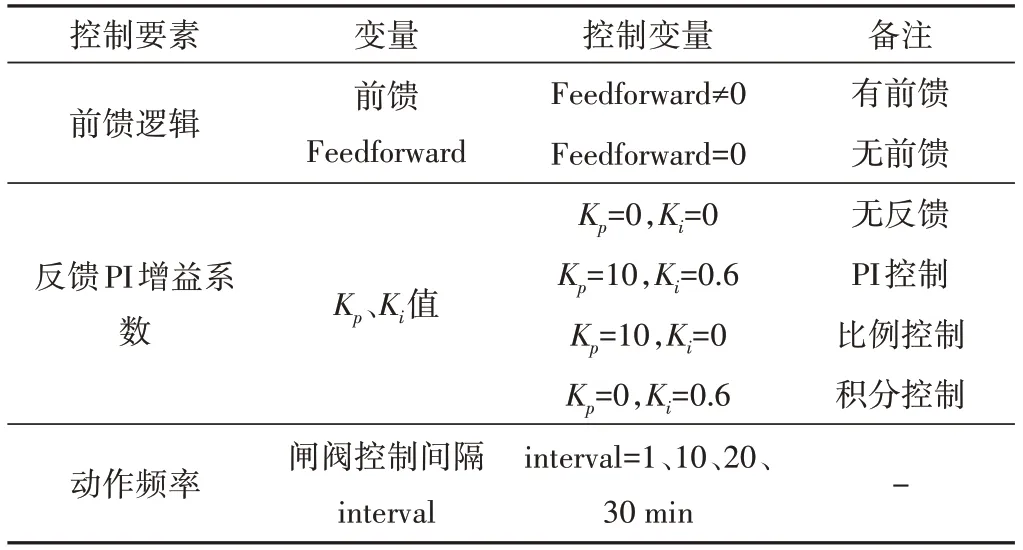
表1 控制要素表Tab.1 Elements of control

3 模型仿真及结果分析

3.1 仿真渠段及参数配置

安揭引韩灌区是韩江粤东灌区的重要组成部分，其设计灌溉面积为1.184 万hm2，全长接近19 km。本文选取前9.6 km作为仿真对象，即从潮州供水枢纽坝（可视为水库）上取水，经由2 300 m 的管径3 m 的管道和340 m 的倒虹吸引水至安揭干渠渠首，干渠由3 个渠道和2 个节制闸组成，设计流量10.37 m3/s。对渠道进行概化建模后，渠段的几何参数和水力特性见图3和表2。

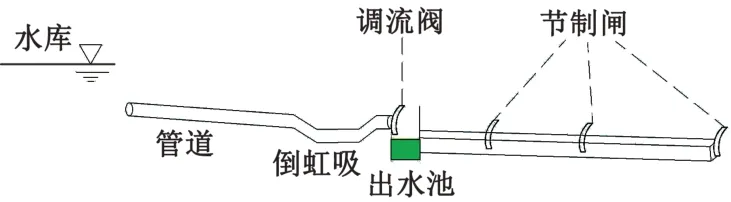
图3 仿真渠段示意图Fig.3 Schematic diagram of simulated canal

表2 仿真渠池的几何参数及水力特性Tab.2 Geometric parameters and hydraulic characteristics of simulation canals

仿真的边界条件和初始条件为：①边界条件：管道为上游水位边界、下游流量边界；渠道为上下游流量边界。②初始条件：等体积运行，通过设计水深求各渠段体积，反算各渠段初始下游水深，得到初始水面线。

3.2 评价指标

为对仿真结果进行更好的评价和分析，本文采用了以下评价无量纲化指标[14]，各项指标越小，代表控制性能越好，见表3。

3.3 仿真计算及结果分析

3.3.1 PI参数比较

通过对不同PI 参数的工况进行仿真，得到在不同PI 控制参数下的控制指标，如表4及图4所示。

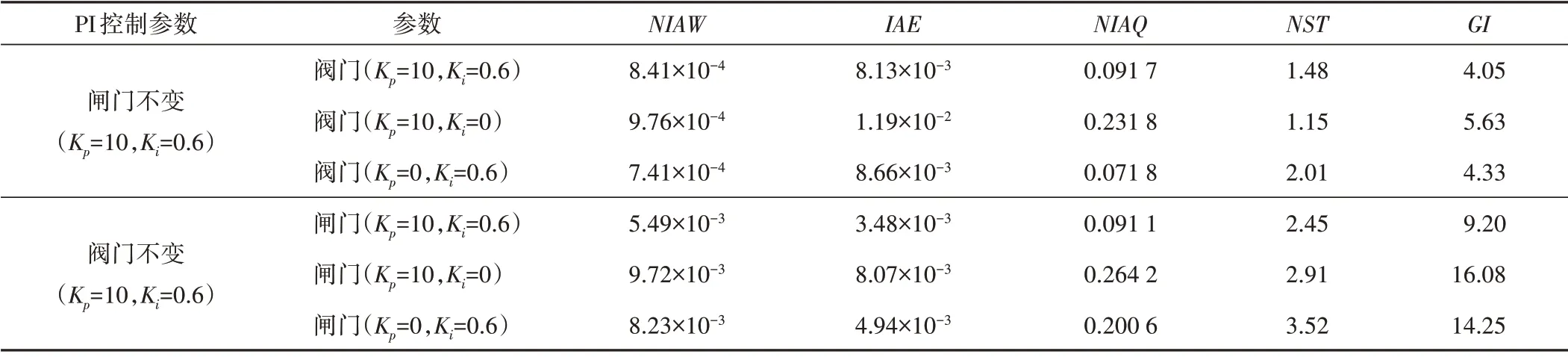
表4 PI控制参数对比表Tab.4 Comparison of PI control parameters

（1）阀门采用比例控制（Ki=0），相较PI 控制，阀门的NST要小22%，但IAE变大了46%、NIAQ变大了1.5 倍，GI变大了39%，图4(a)也可以直观地看出这些变化，这表明水位流量的波动非常剧烈，且存在一定稳态误差。这是因为积分Ki的作用主要为消除静差，Ki=0意味着不需要对静差进行修正，稳定速度就更快了，水位流量波动就更大了，最后也自然会存在稳态误差。

（2）若阀门采用积分控制（Kp=0），相较PI 控制，NIAW要小12%、NIAQ要小22%，但NST变大了36%，GI变大了17%，图4(a)也可以直观地看出这些变化。这是因为比例Kp的作用主要为调节当前时刻误差，Kp=0 意味着不存在有差调节，NIAW、NIAQ的波动就减小了，稳定时间就更长了。

（3）对阀门而言，几种控制方法各有优劣，可结合不同的管道特性进行选择。对于长度较长的管道，为更快地达到稳定效果，可仅采用比例控制；对于不能出现剧烈流量震荡的管道，可仅采用积分控制。一般而言，采用PI 控制能够适应绝大多数的情况。

（4）PI 控制对闸门的控制作用更明显，由图4(b)可以看出，若不用PI 控制，闸门各方面控制性能都会显著变差。仅采用比例或仅采用积分控制相较PI 控制，NIAW分别变大了77%、50%，IAE分别变大了130%、42%，NIAQ分别变大了190%、120%，NST分别变大了19%、44%；GI值分别变大了75%、55%，因此闸门控制最好采用PI控制。

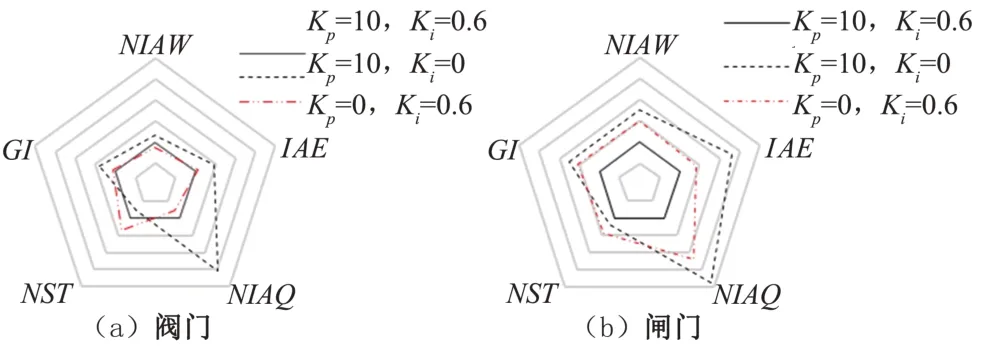
图4 闸阀PI参数对控制指标的作用Fig.4 The effect of gate and valve PI parameters on control indicators

（5）NIAW与NIAQ有一定的相关性。因为闸阀开度变化会引起过闸或过阀流量的变化，而死区的存在使NIAQ波动比NIAW更剧烈。

（6）闸门的NST是阀门的2倍以上。这是因为阀门水力响应速度更快，稳定时间更短。

3.3.2 前馈及反馈

对阀门进行有无前馈、反馈的控制对比，结果如表5和图5所示。

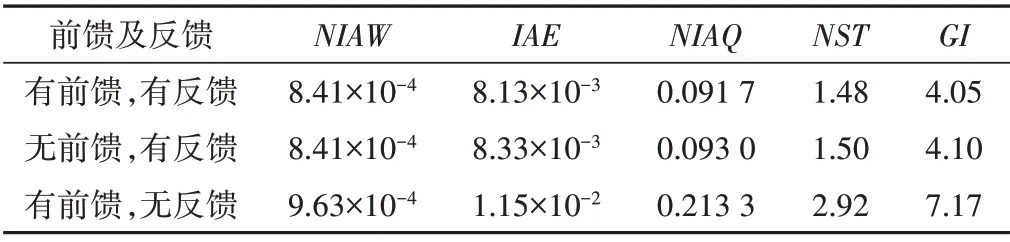
表5 阀门有无前馈及反馈对比表Tab.5 The comparison of valve with and without feedforward and feedback

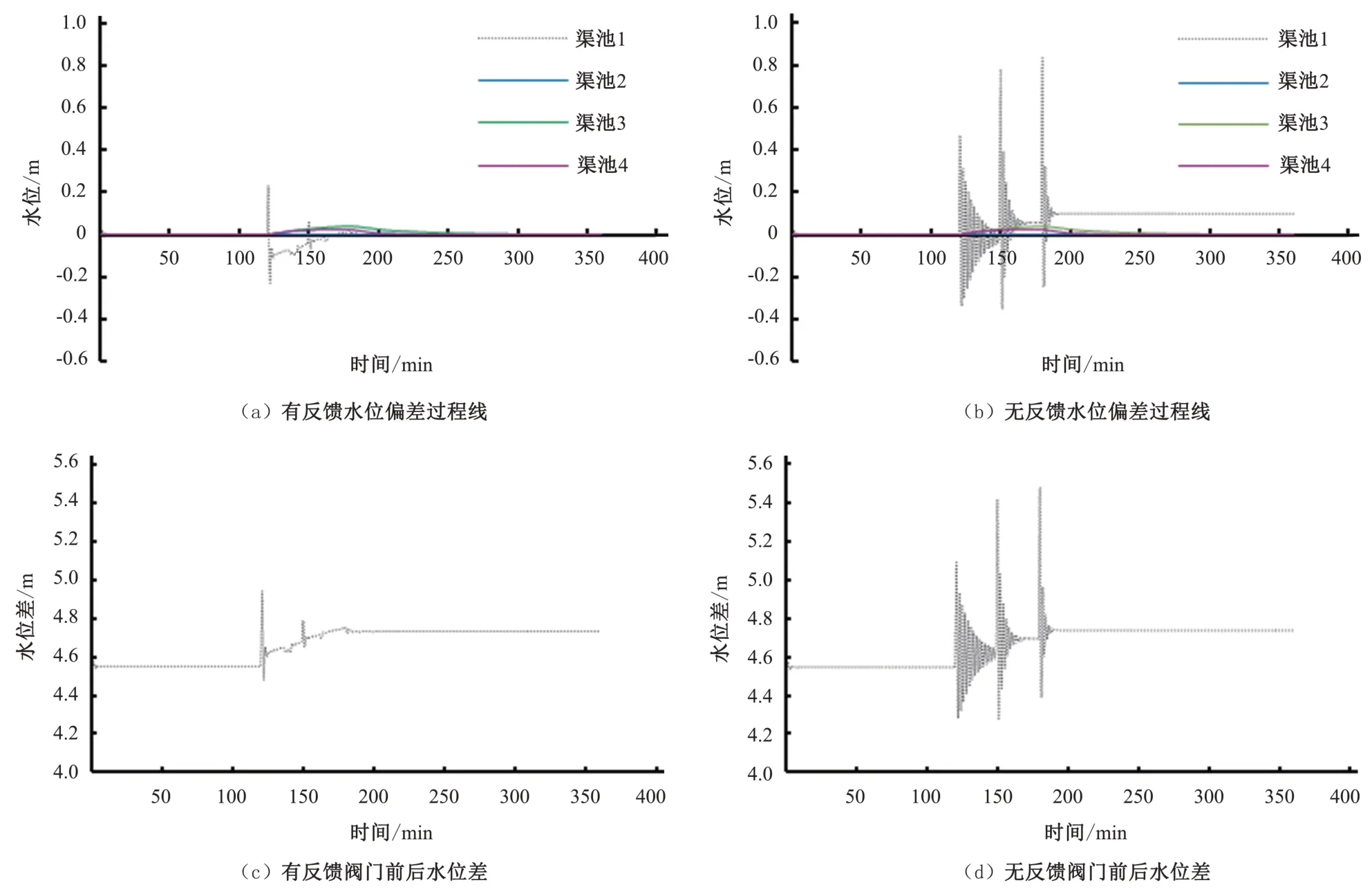
图5 阀门有无反馈对比图Fig.5 The comparison of valve with and without feedback

（1）阀门采用无前馈控制，NIAW没有变化，而其他指标都有小幅的增大，但总的来说，管道可以采用无前馈控制。这是因为前馈的作用是考虑渠池间的时间滞后，制定出各闸门的预分配流量，而管道本身水力响应速度较快，时间滞后较小，无需前馈也能达到理想的控制效果；

（2）若阀门进行无反馈控制，NIAW增大了14%，IAE增大了42%，NIAQ增大了1.33 倍，NST增大了1 倍，其各项指标均出现大幅增大，且出现了明显的水位偏差，控制效果显著变差，水位流量波动非常剧烈。因此，阀门最好采用反馈控制。

3.3.3 闸阀控制间隔

对闸阀的不同控制间隔进行对比，结果如表6和图6所示。

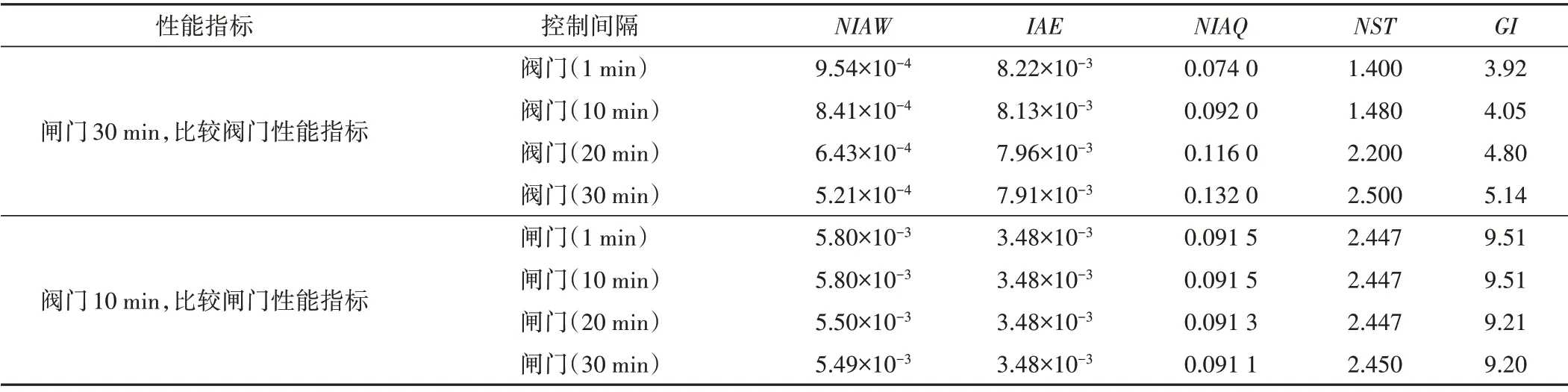
表6 不同闸阀控制间隔对比表Tab.6 The comparison of gate and valve control interval

（1）对于阀门而言，控制间隔1 min 时各项性能指标都比较理想。由图6(a)可知，随着控制间隔的增加，NIAW逐渐减小，NIAQ和NST逐渐增大。这是因为阀门调节频率减小，NIAW也随之减小，稳定时间也会更长。

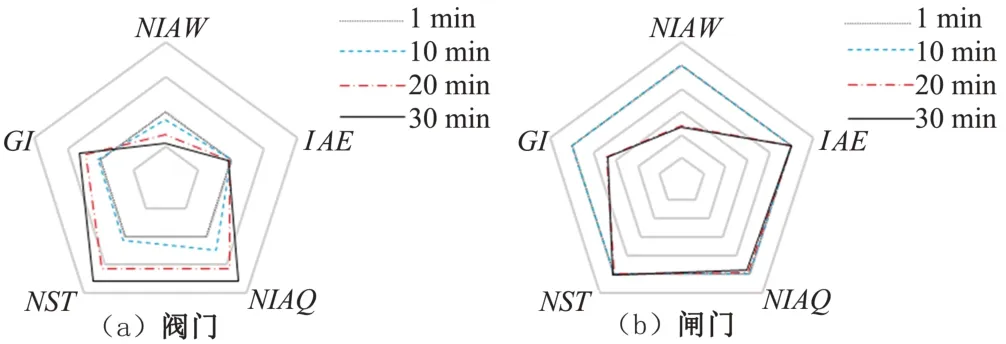
图6 闸阀控制间隔对控制指标的影响Fig.6 The effect of gate and valve control interval on control indicators

（2）对于闸门而言，控制间隔的改变对结果的影响很小，各项指标相差均不超过3%，由图6(b)可知，闸门控制间隔增大对各指标的影响不是很大，尤其是IAE和NST几乎不变。这是因为相对管道，渠道的水力响应速度较慢，闸门的控制间隔变化的影响也较小。

（3）实际工程中，阀门不可能以1 min 的控制间隔工作，因此阀门10 min、闸门30 min的组合控制效果较为合理。

4 讨 论

国内外学者在明满流非恒定流的研究上做了大量的工作，并取得了许多成果。由于管道的弹性波波速与明渠重力波波速有着数量级的差异，管道和渠道联合调控的响应特性也是相差巨大，两者的控制往往难以同步。探索两者的同步控制有利于保障灌区的节水灌溉，实现灌区和输配水系统的安全、高效及自动化运行。基于此，本文采用数值模拟的方法，在处理一维明满流数值计算时采用窄缝法将有压流控制方程与明流控制方程统一，选择管渠结合系统的前馈逻辑与反馈算法中的PI 增益系数与动作频率几个要素进行研究对比，结果表明：①阀门无前馈时控制效果仍较为理想。由于前馈的作用是考虑渠池间的时间滞后，制定出各闸门的预分配流量，而管道本身水力响应速度较快，时间滞后较小，无需前馈也能达到理想的控制效果。②阀门最好采用反馈控制。阀门进行无反馈控制时，NIAW增大了14%，IAE 增大了42%，NIAQ增大了1.33 倍，NST增大了1 倍，各项指标均出现大幅增大，且出现了明显的水位偏差，控制效果显著变差，水位流量波动非常剧烈。③相较PI 控制，阀门仅采用比例或仅积分控制时，综合性能指标GI分别变大了39%、17%，闸门仅采用比例或仅积分控制时，综合性能指标GI分别变大了75%、55%。④由于闸阀控制间隔对管道的影响大于对渠道的影响，考虑工程实际的情况下，阀门控制间隔10 min，闸门控制间隔30 min时，系统的控制效果最好。

5 结 论

本文探讨了管渠结合系统中闸门与阀门的调控方式和控制逻辑的差异性，并通过仿真实验得到了以下结论：

（1）管渠结合系统的调控中，阀门可采用无前馈控制。由于前馈的作用是考虑渠池间的时间滞后，制定出各闸门的预分配流量，而管道本身水力响应速度较快，时间滞后较小，无需前馈也能达到理想的控制效果。

（2）管渠结合系统的调控中，阀门建议采用反馈控制。阀门进行无反馈控制各项性能指标均出现大幅增大，尤其是NIAQ增大了1.33倍。

（3）阀门可根据管道特性选择不同的控制方式，而闸门则最好采用PI 控制。长管道可仅采用比例控制，避免剧烈流量震荡的管道可仅采用积分控制，PI 控制则能适应绝大多数情况。

本文的研究结果对长距离输水管渠结合系统具有借鉴意义，其合理应用可以推动管道和明渠的一体化调控，提高工程的供水效率，保证工程的安全运行。但本文由于的模拟仿真的限制，还存在模型简化、闸阀数量较少的局限性，尤其是阀门在调节过程中的动态流量关系对于调控过程影响较大，同时亦应在当前固定控制逻辑的基础上进一步探索自适应、智能化控制算法。