考虑脉动风场的3 MW 风机钢塔筒基础底板脱开失效概率

2021-05-25蒋友宝贺广零彭穗湘郑峻林

工程力学 2021年5期

蒋友宝，刘志，贺广零，彭穗湘，郑峻林

(1. 长沙理工大学土木工程学院，湖南，长沙 410004；2. 华电重工股份有限公司，北京 100070)

开发风能是解决能源短缺和环境污染两大基本问题的有效措施之一。因此，风能技术在国内外得到大力发展。中国从2005 年基本没有风电发展到2017 年累计装机量已经占世界总量的35%[1-2]。风机作为高耸结构，其基础结构的变形特征、力学条件及塔筒的二阶效应决定了它自身的整体稳定性。大量的风机倒塌事故表明[3]：如果基础失稳，必定会引起风机倒塌等灾难性的后果；而导致灾害的直接原因主要有地基承载力失效、地基不均匀沉降等恶劣的地质环境，以及雷暴、冰冻、强风、暴雨等不良的气候条件。例如在强风荷载作用下，风机塔筒时常发生折断、基础底板脱开等，对风机的安全生产构成重大威胁，该现象已引发了国内外许多科学研究工作者的关注[4-6]。

与一般建筑结构不同，风机所承受的荷载中叶轮气动力一般起控制作用，且该气动力受风速影响较大。因此，对各种风速工况下风机塔筒及风机基础进行力学分析，明确其受力情况是保证风机结构安全的前提条件。对风场作用下风机受力的研究，需考虑脉动风的影响。一般可通过现场实测或者风场模拟[7]等手段获得脉动风时程，再将之用于风机动力响应研究[8-9]。同时，为考虑不确定性因素的影响，风机可靠度的研究也受到较多关注[10-11]。贺广零等[12-13]基于广义概率密度演化理论提出了风机抗风动力可靠度分析方法；通过模拟随机脉动风场，建立了“桨叶-机舱-塔体-基础”一体化有限元模型，分析了风力发电钢塔和钢筋混凝土风力发电高塔的抗风动力可靠度。

目前，对风机基础底板脱开失效概率的研究较少，而实际工程中，因基础底板脱开导致风机破坏的安全事故时有发生。鉴于此，本文结合某3 WM 风力发电高塔系统，分析此类结构在不同风速工况下的基础底板脱开失效概率，并计算其不脱开失效的可靠度，为风机基础设计提供参考。

1 风机塔筒结构模型与荷载计算

1.1 塔筒结构模型

某陆上风电场位于非抗震区，选用3 MW 风机，其叶轮半径为53 m，共有3 个叶轮，尺寸为53 m×2.8 m×3.6 m(长×宽×高)，塔筒总高度为87.423 m，分为上、中、下三段。塔筒上、中、下段高分别为30 m、30 m、27.423 m，分别由14 个、13 个、12 个变截面塔节组成[14]。塔筒顶部筒体直径为3.524 m，塔筒底部筒体直径为4.181 m，中间塔筒半径、高度和壁厚都随高度而变化。风机塔筒简图见图1，具体尺寸见表1。

图 1 风机塔筒简图Fig. 1 Diagram of wind tower tube

1.2 塔筒结构荷载

大型风机塔筒的顶部安装有风机叶轮，在风场作用下叶轮转动产生较大的气动力，且叶轮等装置的重力相对下部塔筒形心有偏心，会产生偏心力矩。相关研究[15-16]表明：塔顶偏心力矩荷载的数值远小于塔顶气动荷载对塔筒底部所造成的弯矩。因此，研究塔筒底部受力时，可对风机塔筒荷载进行简化，即忽略塔顶偏心力矩的影响，将塔筒所受荷载简化为风轮及机舱重力Fy、气动荷载Fx及沿塔筒高度作用的风荷载ωz。其中对于风荷载，主要按顺风向荷载效应考虑。塔筒具体受力见图2。

表 1 钢塔筒分段尺寸Table 1 Size of steel tower

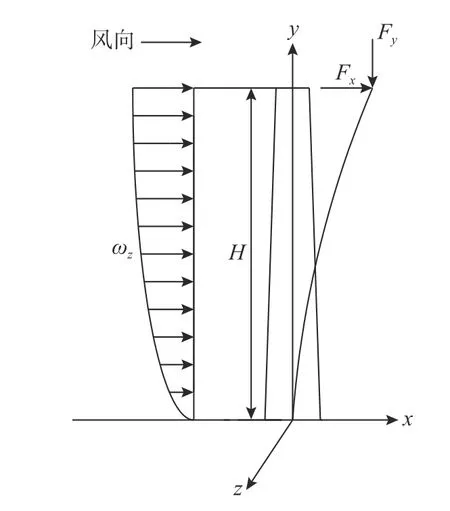
图 2 塔筒承受荷载简图Fig. 2 Loads of wind tower

对于塔身风荷载，《高耸结构设计规范》(GB 50135-2006)[17]规定垂直于风机塔筒表面上的风荷载标准值按式(1)计算：

对于塔筒风机叶轮气动荷载，按两种情形：正常运行工况和极端荷载工况予以考虑。

在正常运行工况下，根据动量-叶素理论叶轮气动推力可计算为：

对于塔顶重力荷载，可按下式计算：

式中：m1为叶轮质量；m2为机舱质量；g为重力加速度。

图 3 不同风速下叶轮推力系数Fig. 3 Thrust coefficient of impeller with different wind speeds

根据3 MW 风机厂家的风机总体技术手册可知：叶轮和机舱的质量分别为66.7×103kg 和127.7×103kg。风机塔筒的塔顶气动力按式(6)、式(7)计算，风机塔筒的塔顶竖向荷载按式(8)计算。

1.3 脉动风场数值模拟方法

为了较为精确模拟整个塔筒受脉动风速的影响，将塔筒等效为一个39 点的高耸结构模型，各质点均位于该节塔筒的中心点，见图4。

图 4 风机塔筒结构模型Fig. 4 Wind tower structure model

利用谐波合成法理论及脉动风场模拟方法[7]。所模拟的脉动风速可表达为：

表 2 风速模拟的主要参数Table 2 Main parameters of wind speed simulation

在风工程领域，应用广泛的风速谱有Davenport谱、Kaimal 谱[19]等。其中Davenport 谱的表达式为：

根据本节介绍的风场数值模拟方法和基本参数，利用MATLAB 程序语言编写模拟单点水平脉动风速时程的程序，进行风场模拟。为了校核整个塔筒模拟所得到的脉动风速是否精确，本文在塔筒的下段取点1、5、10，中段取点15、20、25，上段取点30、35、39，并且将这些点的脉动风速时程功率谱与目标谱(Davenport 谱和Kaimal谱)进行对比分析。可知，两种工况下大部分点的脉动风速模拟效果比较好，少数点虽然偏差稍大，但均在工程容许范围内。限于篇幅，仅给出点5 的风速功率谱与脉动风速对比以及选用Davenport谱和Kaimal 谱的总风速对比情况，见图5。

2 风机塔筒结构动力时程分析

2.1 风机塔筒结构有限元模型

图 5 点5 风速功率谱与总风速对比Fig. 5 Comparisons between power spectrums of wind speed and total wind speed for point 5

彭文春等[15]、袁万等[20]采用ABAQUS 软件对风机钢塔筒进行了建模，结果表明分析效果较好。参考该思路，采用ABAQUS 软件按图1 和表1 建立风机钢塔筒模型。假定风机钢材材料为Q345E，密度为7850 kg/m3，弹性模量为2.1×1011Pa，泊松比为0.3。为简化分析，本文参考文献[21]假定底面考虑为固定约束，各塔筒段之间采用绑定(tie)约束。

2.2 塔筒的模态分析

先对该风机塔筒结构进行模态分析。Tempel等[22]将塔筒顶部的机舱和叶轮等效为一个质点，并赋予质量，且将此质点与塔筒顶部圆环截面进行耦合。参考该思路，选用ABAQUS 中Lanczos算法进行模态分析，分析结果见表3。

表 3 塔筒前六阶固有频率Table 3 First six natural frequencies of tower

根据塔筒的第1 阶、第2 阶固有频率，按Rayleigh阻尼考虑，对应的阻尼系数 α、λ分别为：

式中：ω1、ω2分别为第1 振型、第2 振型的圆频率，ω=2πf′，f′为塔筒的固有频率； ξ为振型阻尼比，根据《高耸结构设计规范》(GB 50135-2006)[17]钢结构阻尼比取0.01。

从表3 可知，风机塔筒的第1 阶、第3 阶、第5 阶的固有频率分别与第2 阶、第4 阶、第6 阶相同，这是因为风机塔筒在x与z方向对称，即风机塔筒在这两个方向的刚度和质量相同，这与赵志等[23]的研究结果相吻合。风机塔筒的第1 阶固有频率为0.281 与厂家所提供的数据0.283相差仅0.71%，表明本文将叶轮与机舱的质量考虑为风机塔筒本身质量与原模型基本等效。根据式(11)、式(12)得出 α、λ分别为0.0176 和0.005 67。

2.3 塔筒的动力时程分析

由式(2)～式(7)，可分别计算出塔筒风荷载和叶轮气动推力荷载；再考虑塔筒、叶轮和机舱的自身重力，便可得到塔筒的总荷载。将这些荷载分别输入到ABAQUS 有限元模型中，其中塔顶叶轮和机舱的重力荷载按模态分析时以点质量的形式预先施加，与实际情形相符；而风荷载和叶轮气动推力时程总长度为200 s，时间间隔为0.2 s，采用隐式分析法进行计算。为使计算结果更为精确，动力时程分析中考虑重力二阶效应的影响。对于该塔筒结构，选用Davenport 谱、Kaimal 谱模拟脉动风速得到的荷载效应均有较大波动。限于篇幅，仅列出选用Davenport 谱模拟脉动风速时正常运行工况与极端荷载工况下塔筒底部的弯矩时程曲线以及产生最大应力时间点的应力云图，见图6。

图 6 选用Davenport 谱时两种工况下动力时程分析结果Fig. 6 Results of dynamic time history analysis under two working conditions using Davenport spectrum

可见，当采用Davenport 谱时，在正常运行工况下：塔筒底部最大的弯矩为5.85×107N·m，最大应力为135 MPa；在极端荷载工况下：塔筒底部最大的弯矩为1.10×108N·m，最大应力为286 MPa。由于钢材屈服强度为345 MPa，两种工况下最大应力值均小于钢材的屈服强度，满足强度要求。

3 风机塔筒基础脱开失效概率

3.1 风机塔筒结构荷载效应统计模型

如前所述，由于风机塔筒所受风荷载和叶轮气动推力都会随时间的变化而变化，因而塔筒底部的剪力和弯矩等作用效应波动变化显著。记Sk为作用效应的标准值，分别按规范[17]设计方法和式(6)、式(7)计算确定风荷载和叶轮气动力的标准值，并利用有限元静力分析得出两种工况下塔筒底部弯矩M、剪力V、轴力N的标准值，计算结果见表4。

表 4 作用效应标准值Table 4 Standard value of action effect

记μ为其对应的作用效应均值。定义一系数κ，其计算式为：

先对两种工况下分别按式(6)和式(7)计算的塔筒顶部气动推力进行统计分析，所得结果见表5。可见，无论是选用Davenport 谱还是Kaimal 谱，正常运行工况下叶轮气动推力的变异性均较极端荷载工况要小一些。而相同运行工况下，按Davenport谱考虑时叶轮气动推力的变异性要大一些。

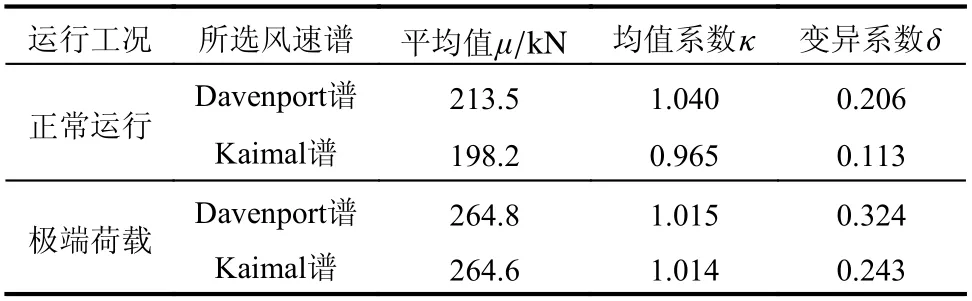
表 5 风荷载时程下塔顶气动推力的统计参数Table 5 Statistical parameters of aerodynamic thrust on tower top under wind load time history

根据第2.2 节的动力时程分析，可对各作用效应的结果进行统计分析。例如对于塔筒底部弯矩和剪力，其频数直方见图7。

图 7 弯矩和剪力频数直方图Fig. 7 Frequency histogram of bending moment and shear

对弯矩、剪力时程分析结果进行相关性分析表明：采用Davenport 谱时，正常运行和极端荷载工况下的弯矩、剪力的相关系数分别为0.981 和0.873；采用Kaimal 谱时，正常运行和极端荷载工况下的弯矩、剪力的相关系数分别为0.955 和0.805。为简化考虑，假定两者完全相关。若用极值I 型分布来拟合，部分拟合效果对比见图8。可知，在图8(a)中，全段曲线拟合效果较好；在图8(b)中，当累积分布概率大于0.5 时，曲线拟合效果较好；在图8(c)中，当累积分布概率大于0.3 时，曲线拟合效果较好；在图8(d)中，当累积分布概率大于0.4 时，曲线拟合效果较好。需说明的是，上述区域正是对失效概率有重要贡献的区域，虽然其他区域的拟合效果较差，但对失效概率的影响较小，即对可靠度的计算结果影响不大。因此，本文假定正常运行工况与极端荷载工况下塔筒底部的弯矩和剪力均为极值I 型分布，且完全相关，相应的统计参数见表6。

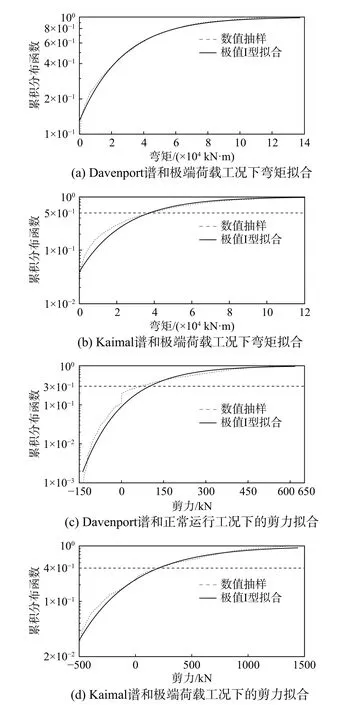
图 8 弯矩和剪力的极值I 型拟合曲线Fig. 8 Extreme value I-type fitting curve of bending moment and shear force

由表6 可知，塔底弯矩、剪力的变异系数较表5 中风机气动力变异系数高出较多。原因主要是塔筒受自身高度范围内的脉动风场影响较大，且重力二阶效应显著，使得总效应的变异系数较风机气动力有较大增加。

3.2 标准模型基础底板脱开失效概率

风机基础主要承受上部结构传来的作用以及自身和覆土自重，见图9，其中M、F为风机上部结构传递过来的弯矩、水平力；N为风机上部结构传递过来的轴力；N1为基础混凝土自重；N2为基础以上覆土自重；R为基础底板半径；h为上部荷载作用点到基础底部的距离。

表 6 动力时程分析作用效应的统计参数Table 6 Statistics of load effects in dynamic time history analysis

图 9 风机基础受力简图Fig. 9 Wind power foundation diagram

表 7 基础竖向力效应统计参数Table 7 Statistics of vertical force effect of foundation

受各种不确定性因素的影响，偏心距e将具有较强的随机变异性，因而存在脱开的可能。此处除考虑上部结构自重、混凝土容重、覆土容重等变量的随机变异性外，还考虑了作用效应的随机变异性。其统计参数见表8。

表 8 随机变量的统计参数Table 8 Statistics of random variables

由于基础脱开会造成塔筒倾覆，因此，按首超破坏准则建立失效方程。由《陆上风电场工程风电机组基础设计规范》(NB/T 10311-2019)[27]和《高耸结构设计规范》(GB 50135-2006)[17]可知，正常运行工况下风机基础脱开面积比不大于0，即底板偏心距e与基础半径R的比值不超过0.25；极端荷载工况下脱开面积比不大于25%，即底板偏心距e与基础半径R的比值不超过0.43。按该要求，正常运行、极端荷载工况下基础底板脱开的极限状态方程分别为：

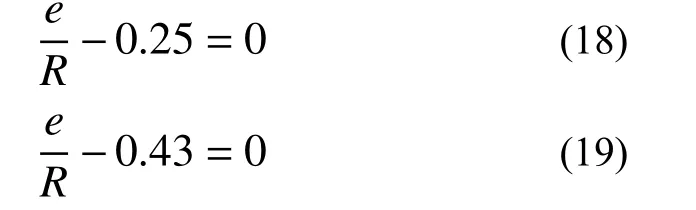
采用Monte Carlo 法，选用Davenport 谱计算得到正常运行和极端荷载工况下风机基础底板脱开失效概率Pf分别为0.008 20 和0.0188，选用Kaimal谱计算得到的对应Pf分别为0.0107 和0.0281。

则选用Davenport 谱时两种工况下风机基础底板不脱空失效的可靠指标分别为2.40 和2.08，而选用Kaimal 谱时可靠指标分别为2.30 和1.91。

3.3 底板半径变化时基础不脱开失效的可靠度

从式(18)、式(19)可知，底板半径对基础底板不脱开失效的可靠度影响较大。为此，研究底板半径变化时风机基础底板可靠度，计算结果见表9、表10。记 η表示风机基础底板不脱开失效的可靠指标的变化的程度：

式中， βi为第i种基础底板半径下基础底板不脱开失效的可靠指标。

表 9 正常运行工况下风机基础底板不脱开失效的可靠指标Table 9 Reliable indicators without failure of wind turbine foundation slab void under operation condition

表 10 极端荷载工况下风机基础底板不脱开失效的可靠指标Table 10 Reliable indicators without failure of wind turbine foundation slab void under extreme load condition

结果表明：两种工况下底板半径对基础底板不脱开失效的可靠度的影响的确较大。当将底板半径降至0.8 倍时，正常运行工况下按Davenport谱和Kaimal 谱计算得到的可靠指标分别降低约44.58%和44.78%，极端荷载工况下分别降低约40.87%和45.03%。当半径增加至1.2 倍时，可靠指标均会有较大的(不小于39.90%)提升。例如，对于正常运行工况，按Davenport 谱计算得到的可靠指标提升为3.41，提高约42.08%，按Kaimal 谱计算得到的可靠指标提高约46.09%。