地铁轮轨耦合不平顺激励对轨道振动影响分析

2021-05-25李明航谭新宇曲翔宇张厚贵

工程力学 2021年5期

马蒙，李明航，谭新宇，曲翔宇，张厚贵

(1. 北京交通大学土木建筑工程学院，北京 100044；2. 北京市劳动保护科学研究所，北京 100054)

地铁列车运行引起的振动由车辆、轨道相互作用产生，经由轨道结构、隧道结构、地层及建筑基础，传至敏感建筑内部引起结构振动及二次噪声，对楼内居民生活和建筑功能造成潜在影响。在地铁线路方案设计阶段，建立合理的预测模型提高环境振动预测的准确性对优化地铁线路设计和综合减隔振设计起到重要作用[1-3]。车辆-轨道动力相互作用的模拟决定了环境振动预测模型中振源子模型的准确性。列车移动荷载可视作准静态分量和动态激励的叠加[4]，准静态激励由移动的列车轮轴荷载引起，而动态激励则受轨道不平顺、车轮不圆顺等引起的随机激励，以及轨道结构周期性等固定参数激励影响。

轨道不平顺和车轮不圆顺通常可以视为平稳的随机过程，采用功率谱密度函数(Power Spectral Density, PSD)表达。针对高速铁路和干线铁路轨道不平顺，主要采用德国谱、美国谱或实测值作为车辆-轨道激励[5-6]。而针对地铁建立的车辆-轨道耦合模型中，由于缺少被广泛认同的轨道不平顺谱，通常将美国谱[7-9]或实测钢轨表面粗糙度作为输入激励[10-11]，近年来也有越来越多的研究针对不同波长成分采用不同模拟方法[12-13]。文献[14 - 15]的测试和模拟结果表明，车轮的磨耗状态对环境振动关心的频率有显著影响。此外，温士明等[16]对比测试了车轮镟修前后浮置板轨道的振动响应；Nielsen 等[17]通过对比分析不同车轮磨耗程度对应的地表振动响应，证明了通过车轮镟修可以有效降低环境振动。然而，目前在预测地铁列车环境振动时，几乎所有研究中均只考虑了轨道不平顺的激励，鲜有文献考虑车轮不圆顺的影响。

为了综合分析轨道不平顺以及车轮、钢轨的磨耗状态对轨道动力响应的影响，本文对一列地铁列车进行了车轮不圆顺的现场测试，同时对一段区间隧道内的轨道不平顺和钢轨粗糙度均进行了测试，并基于测试结果构建了轮轨耦合不平顺谱。应用车辆-轨道耦合频域解析模型计算了轨道动力响应，并比较了不同轮轨激励模式对计算结果的影响。此外，在上述区间隧道内实测了钢轨振动响应，用以验证不同激励模式计算结果的准确性。

1 车轮不圆顺和轨道不平顺测试

1.1 实测车轮不圆顺

为了构建可用于车辆-轨道耦合模型计算输入的车轮不圆顺谱，选取一列6 节编组的地铁B 型车，对全部48 个车轮进行不圆顺测试。该列车至测试时累积运营里程14.1 万公里，尚未进行车轮镟修作业。测试车轮标准半径为0.42 m。测试仪器采用便携式车轮不圆顺测试仪TriTops，该仪器具备3 个等距测量探针，可同时测量距离轮缘外侧70 mm 的名义滚动圆处及其左、右10 mm 处的3 个不同车轮踏面位置的不圆顺(见图1)。测试时先用千斤顶顶升轮对，然后利用永磁铁将测试仪器固定在钢轨上，微调传感器位置使其归零，然后手动转动轮对，仪器自动记录数据，最后拆卸仪器和千斤顶。图2 为测得车轮不圆顺的典型结果。

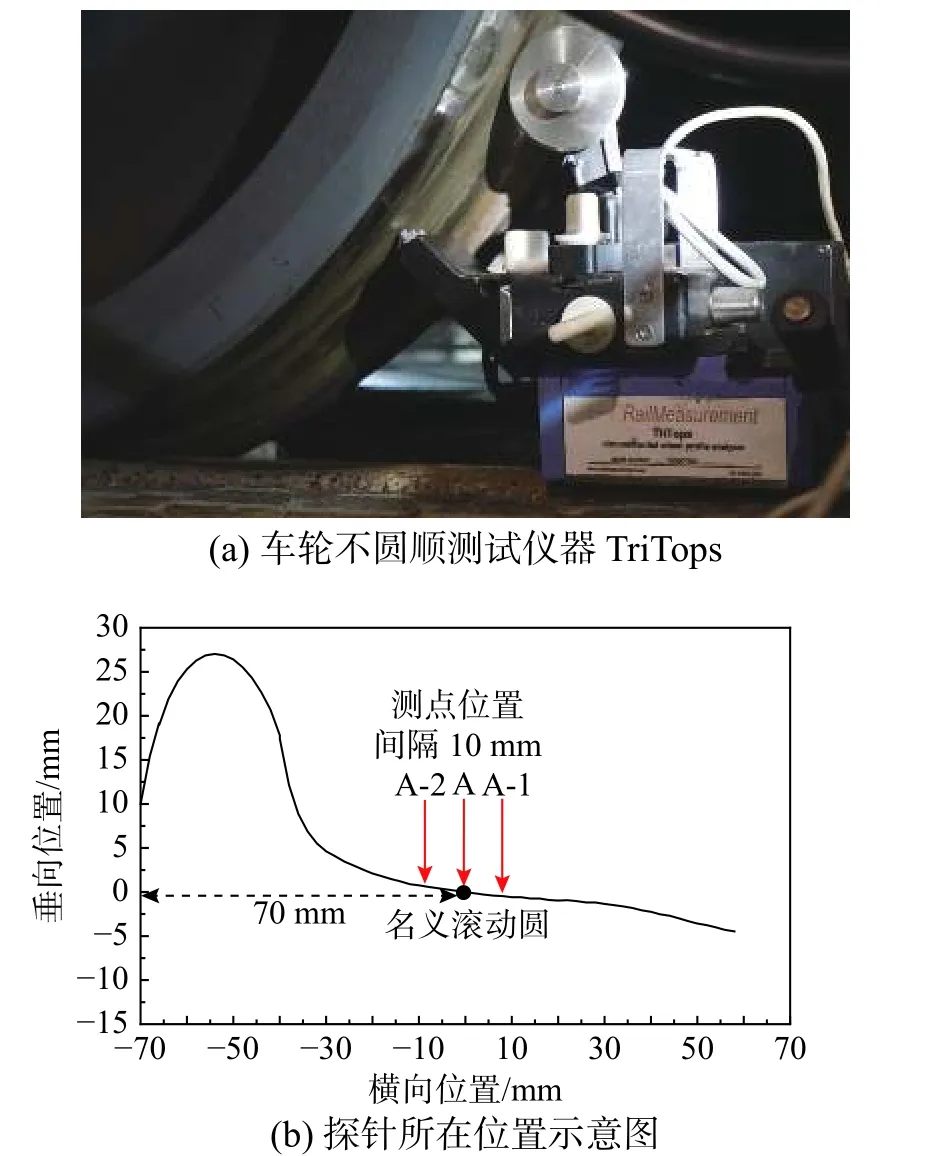
图 1 测试仪器及测点位置Fig. 1 Measurement instrument and sensor locations

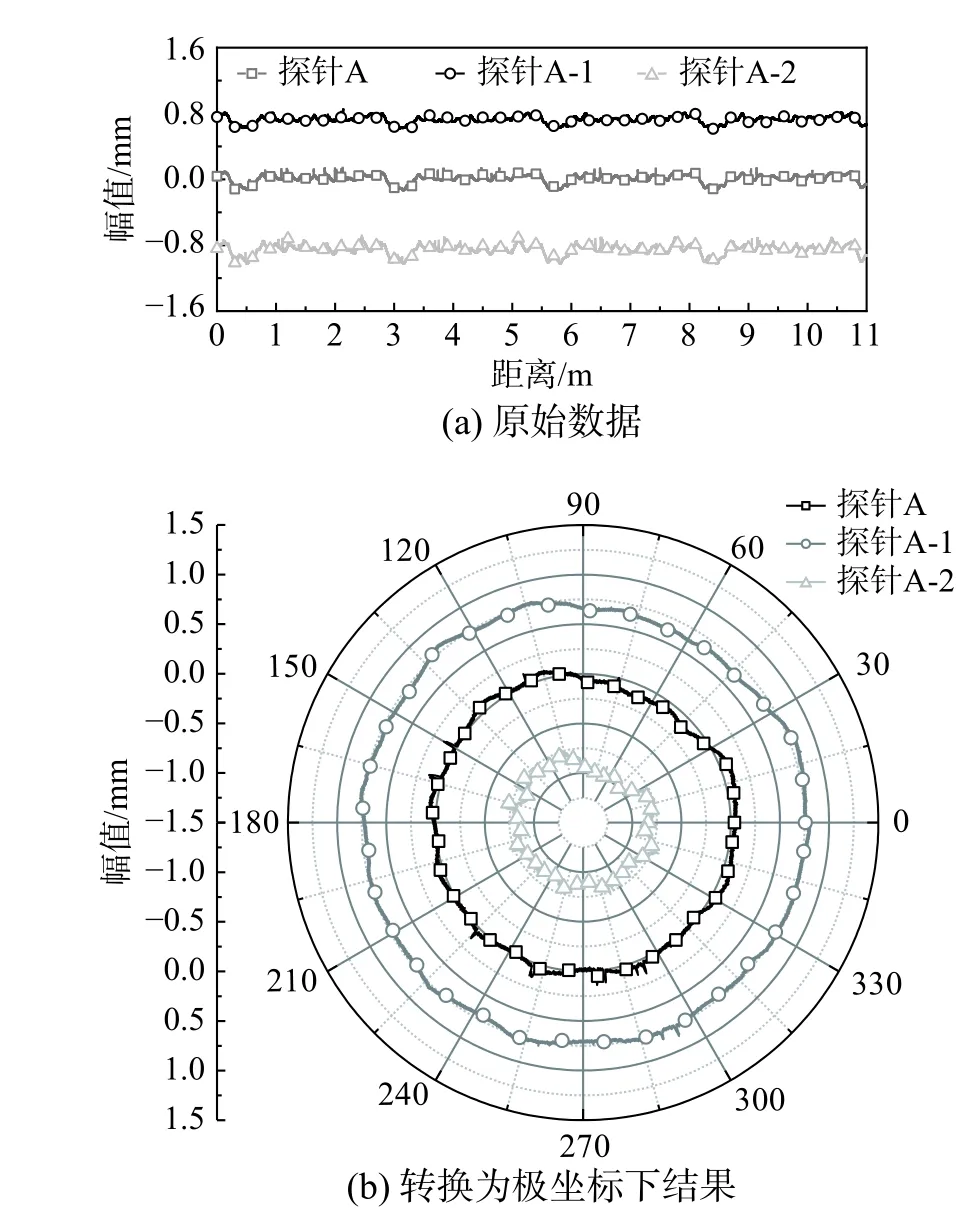
图 2 典型车轮不圆顺测试结果Fig. 2 Typical measurement results of wheel out-of-round

图 3 所有车轮粗糙度谱测试样本及其代表性分位谱Fig. 3 All test sample of wheel roughness PSD and their typical quantile spectrum

采用周期图法进行车轮不圆顺测试样本的功率谱密度函数估计，测试数据加汉宁窗，恢复系数为2。测试样本对应的车轮不圆顺谱及其统计分位数谱如图3 所示。根据文献[18]的研究，随着运营里程的增加，车轮踏面的磨耗量呈现以实际滚动圆为中心的正态分布特征，单位运营里程车轮磨耗量同样呈现正态分布特征。由于测试同一车轮多个测试位置、不同车辆车轮的空间位置不同、簧下质量差异等多个因素作用下，车轮的不圆顺谱幅值差异明显，在某些波长处，相差甚至超过三个数量级；车轮不圆顺谱呈现与各阶多边形磨耗典型波长的峰值，其中7 阶、8 阶、9 阶及14 阶对应峰值尤为突出，60 km/h 运行车速下对应频率为44 Hz、50 Hz、57 Hz 及 89 Hz；此外，均值谱、5%及95%分位数谱呈现相似的波动趋势，三条统计谱线间主要表现为量级的差异。图4 给出了三条车轮不圆顺统计谱与Sato 提出的功率谱[19](简称“Sato 谱”)和美国谱的对比情况，测试列车车轮不圆顺的均值谱及95%分位谱在0.5 m 以下波长段远高于美国1 级谱及Sato 谱。因此可以推测，在地铁车辆-轨道耦合模型中以美国谱或Sato 谱作为输入激励，难以客观反映车轮不圆顺的激励信息。

图 4 实测车轮不圆顺分位谱Fig. 4 Statistic quantile PSD of tested wheel roughness PSD

1.2 实测轨道不平顺

轨道高低不平顺包括动态高低不平顺和静态钢轨表面粗糙度等不同波长成分。为得到待测区间隧道包含不同波长成分的轨道不平顺，采用地铁运营单位提供的该区间轨道动态高低不平顺检测原始数据，其最短分析波长为2 m。采用高精度钢轨波磨测试小车测试该区间的钢轨表面粗糙度(见图5)，测试波长范围为0.01 m～3.000 m。低不平顺谱在2 m～20 m 波长范围内，在美国1 级谱及6 级谱之间波动；0.5 m～2 m 波长段的实测钢轨粗糙度谱与美国1 级谱基本吻合，明显高于Sato谱；0.05 m～0.5 m 以内大部分波长段介于在美国1 级谱及6 级谱之间；粗糙度谱在0.04 m 左右出现明显的峰值，该波长与测试区间的钢轨波磨直接相关。因此，在地铁车辆-轨道耦合模型中，采用不同等级的美国谱作为激励信息，基本可以反映地铁轨道的动态高低不平顺及钢轨粗糙度的状态。

图 5 钢轨表面粗糙度测试Fig. 5 Rail roughness test

图 6 实测轨道动态高低不平顺谱及钢轨粗糙度谱Fig. 6 Measured track dynamic irregularity PSD and rail roughness PSD

2 车辆-轨道耦合频域解析模型

2.1 车辆与轨道控制方程

采用基于MATLAB 的自编程序建立2 维车辆-轨道耦合频域解析模型。地铁列车考虑为6 节编组的B 型车，每节车辆简化为具备2 系质量弹簧体系的10 自由度模型。各子结构均考虑为刚性体，系统方程可以通过对各个刚体各自由度采用D’Alembert 原理计算获得。轨道模型考虑为离散支撑的欧拉梁模型，以模拟整体道床上安装DTVI2型扣件(见图7)。

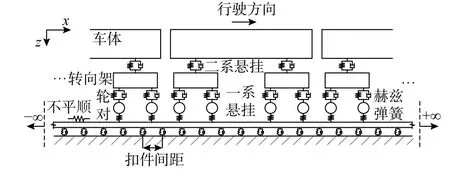
图 7 车辆-轨道耦合模型示意图Fig. 7 Sketch of vehicle-track coupled model

本文旨在分析列车运行引起的环境振动问题，重点关注200 Hz 以下频段的轨道振动响应。根据文献[20 - 23]的研究，在该频段内，采用线性的赫兹弹簧进行轮轨相互作用模拟可以获得可靠的计算结果。因此，轮轨间采用赫兹接触，接触参数见文献[24]；同时将轨道高低不平顺谱(含实测钢轨表面粗糙度谱)及车轮不圆顺谱作为系统激励。

列车第m节车辆的频域控制方程表示为：

依据无限-周期理论，将轨道结构视为以扣件间距L为周期的离散支撑无限-周期结构。钢轨简化为无限长欧拉梁，扣件支撑简化为弹簧阻尼单元，则轨梁的振动响应可统一在一个特征周期长度内进行求解。在频域内，频率为ωl的单位移动荷载作用下，一个特征周期内的轨梁振动方程为：

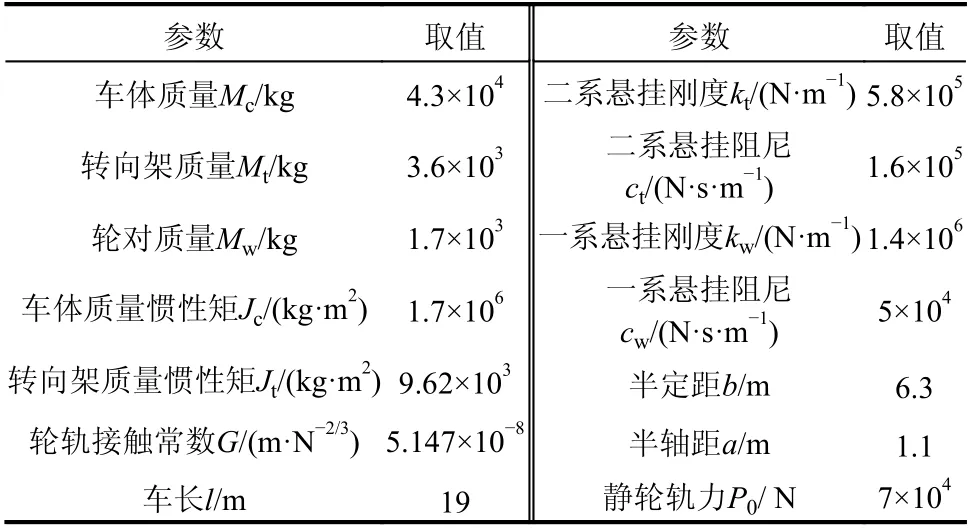
表 1 地铁车辆参数Table 1 Metro vehicle parameters

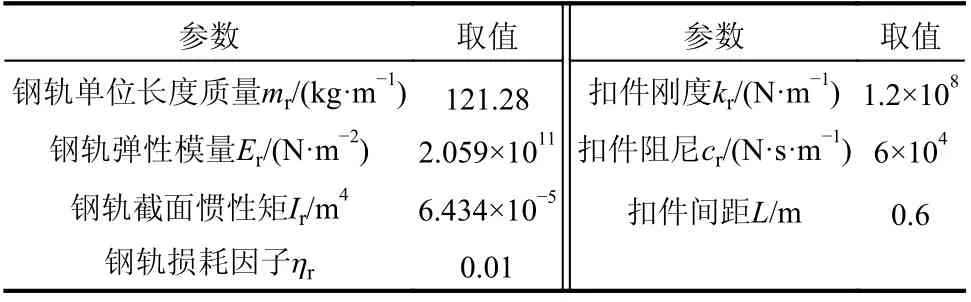
表 2 DTVI2 扣件轨道参数(对应两股轨道)Table 2 Parameters of track with DTVI2 fasteners(corresponding to two rails)

2.2 轮轨耦合不平顺谱

为了综合反映车轮不圆顺和轨道不平顺的耦合激励机制，需要同时考虑轨道动态不平顺、钢轨表面粗糙度及车轮不圆顺(≤2.62 m 波长段)的全部激励能量。由于建立的车辆-轨道耦合模型是2 维的，因此本文涉及的轮、轨不平顺谱均为竖向激励。采用轮、轨分离谱的形式[26]，即分别对车轮踏面及钢轨表面粗糙度谱进行测量估计，按照能量叠加的方式进行线性叠加。该方法假设车轮不圆顺与钢轨表面粗糙度之间完全不相干，保证激励信息的完备与激励能量的等效，综合考虑了轮、轨耦合激励作用。本文重点关注50 mm 以上波长的车轮不圆顺和钢轨不平顺，这一波长远大于接触斑尺寸，因此可忽略接触滤波效应。

轮轨耦合不平顺的拟合以文献[20, 25]中给出的改进三角级数拟合方法为基础，同时考虑车轮不圆顺及轨道不平顺的影响。该方法假设不平顺的样本函数由不同频率成分的谐波分量组成，且不同波长的不平顺是由不同的因素诱发所引起，因此假设不同波长间相互独立。则列车第k轴历经的对应激励频率ωl(l=-NR,···,-1,1,···,NR)的轮轨耦合不平顺幅值可以表达为：

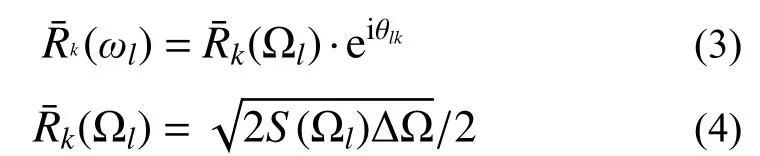
3 轨道动力响应计算与测试

3.1 计算工况

为对比分析多种轮轨激励输入模式下的轨道振动响应，共设计了9 种计算工况(见表3)。其中，轨道不平顺考虑了美国谱、Sato 谱和实测轨道不平顺及钢轨表面粗糙度谱等方式，车轮不圆顺考虑不同实测分位谱。对于实测轨道谱分析工况，≥2 m 波长段，采用测试区间的实测轨道动态高低不平顺谱；＜2 m 波长段，采用实测钢轨表面粗糙度谱。车轮不圆顺谱仅影响≤2.62 m 波长段。

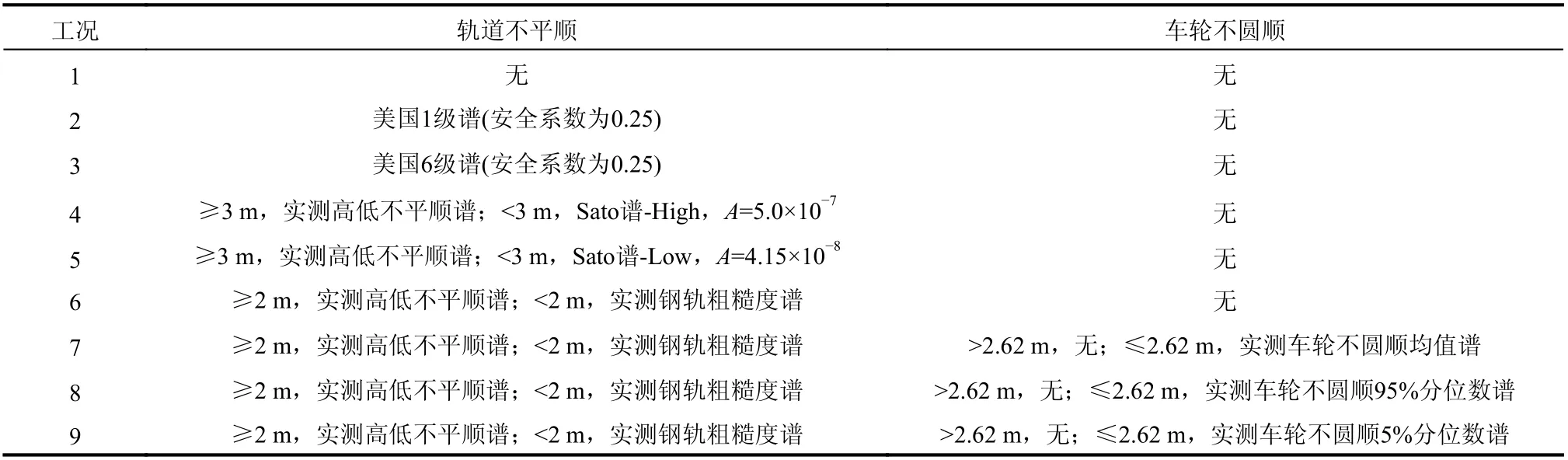
表 3 计算工况Table 3 Calculation cases

图8 为车轮不圆顺谱与实测轨道不平顺谱的耦合谱。当车轮不圆顺程度较轻时，轮轨耦合谱主要表现轨道的不平顺特征，但随着车轮不圆顺程度的增加，车轮各阶多边形磨耗对应的波长处功率谱则越发凸显，幅值远高于美国1 级谱；Sato谱虽然是一种针对3 m 以下的轮轨耦合粗糙度谱，但其量值明显低于实测轮轨耦合不平顺谱。

3.2 计算结果分析

为了评价不同激励工况下轨道响应计算准确性，对实测轨道不平顺和钢轨粗糙度所在地铁区间布设测点，对钢轨垂向振动加速度进行了24 h的连续监测。测点所在断面地铁线路为直线、列车通过车速为60 km/h。根据地铁运营单位提供的线路运营图，提取出测试车轮不圆顺的那一列车多次重复通过钢轨测点断面时的振动响应。

三分之一倍频程频域坐标下的振动加速度级定义为：

式中：a(fi) 为不同中心频率fi处的振动加速度均方根值；a0为参考加速度，取10-6m/s2。

图9 对比了不同轮轨激励工况下钢轨振动响应的计算结果与测试结果。如图9 (a)所示，10 Hz以上全频段，美国1 级谱计算结果高于6 级谱约10 dB，且1 级谱的计算结果在8 Hz～40 Hz 内与测试结果较接近；8 Hz 以下频段的振动响应受准静态激励控制，轨道不平顺的输入对计算结果基本没有影响。图9 (b)给出了Sato 谱对应的计算结果。高等级的Sato 谱对应的计算结果在8 Hz～31.5 Hz频段与测试结果更接近，但仍普遍低于测试结果。此外，Sato 谱虽然作为一种轮轨耦合粗糙度谱在高速铁路运行引起的振动及噪声问题中被广泛应用，但其最高等级的谱值仍无法准确计算50 Hz 以上频段的钢轨振动响应。由图9 (c)可知，在分段输入实测轨道高低不平顺及钢轨表面粗糙度时，16 Hz～31.5 Hz 频段计算结果略高于测试结果。美国谱、Sato 谱及实测轨道不平顺作用下，在50 Hz 以上全频段，计算结果都显著小于测试结果，部分中心频率处差异超过10 dB。图9 (d)给出了输入轮轨耦合不平顺的计算结果，当车轮不圆顺取为均值谱时，计算结果及测试结果在8 Hz以上全频段吻合良好；除80 Hz 外，计算值与测试值相差不超过5 dB；由于本文采用的轮轨耦合不平顺构造方法未考虑车轮表面粗糙度与钢轨表面粗糙度间的相干性，一定程度上高估了轮轨表面的实际激励信息，导致在80 Hz 及其他部分中心频率处，计算结果略高于实测振动加速度。综合比较，考虑车轮不圆顺的影响后，可以完善动态激励信息，尤其是在车轮不圆顺对应的典型波长段会明显提高计算准确性。

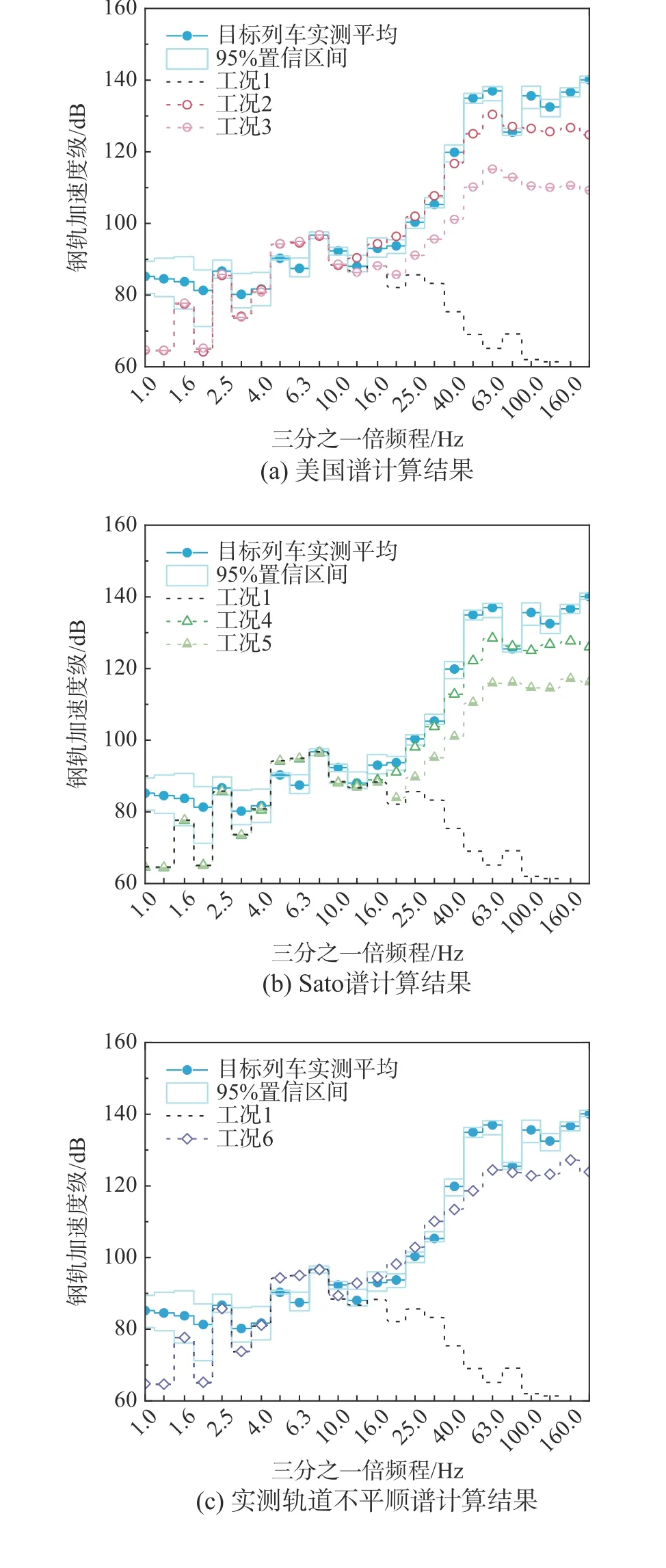
图 9 计算与测试钢轨振动加速度级Fig. 9 Calculated and measured result of rail VAL

3.3 计算结果准确性评价

为定量评价计算结果与测试结果间的差异，引入平均绝对百分比误差(mean absolute percentage error，MAPE)，表示为：

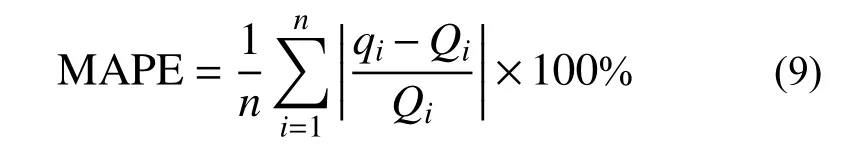
图 10 部分计算工况的平均绝对百分比误差Fig. 10 MAPE of part of calculation conditions

式中：qi表示计算结果；Qi表示测试结果；n表示计算结果与测试结果形成数对的个数。MAPE 越大则计算结果与测试真值相差越大。图10 给出了工况2、工况4、工况6、工况7 的8 Hz 以上的分频MAPE 及全频段的MAPE。考虑车轮不圆顺时：仅在20 Hz～31.5 Hz 及80 Hz 处的MAPE 高于其他工况；绝大部分中心频率处的MAPE 低于1.5%；8 Hz～200 Hz全频段的MAPE 计算结果仅为2.4%，远低于其他工况。