基于相关指标的裂隙岩体渗透系数估算模型研究
2021-05-25钱家忠王德健马海春赵卫东
王 玮,钱家忠,马 雷,王德健,马海春,赵卫东
(合肥工业大学资源与环境工程学院,安徽 合肥 230009)
渗透系数是定量描述地下水在岩石裂隙中流动和运移的基本参数[1],是水文地质的一项重要指标[2],在实际工程中得到了广泛的应用。然而,裂隙岩体具有高度的复杂性和不确定性[3],如何较准确地在野外现场快速确定渗透系数一直是工程应用中面临的难题。
当前,野外获取裂隙岩体渗透系数的方式主要有抽水试验[4]、微水试验[5]、压水试验[6]、排水试验[7-8]、示踪试验[9]以及联合试验[10]等方法,但是这些试验方法普遍耗时长、费用高,不同方法得到的结果差异大。因此,有必要开发一种获取参数灵活、准确率高、快速便捷的估算渗透系数的方法。渗透系数的估算模型作为一种便捷快速的方法已经在工程领域得到广泛的应用。Louis[11]、Black[12]、Snow[13]、Wei等[14]、Carlsson等[15]、Chen等[16]分别总结了渗透系数和深度之间的关系(表1)。蒋小伟等[17]总结提出了岩石质量指标(RQD)与平均渗透系数之间的关系。Hsu等[18]和Ku等[19]提出了一种基于岩石质量指标(RQD)、深度指标(DI)、泥质含量指标(GCD)、岩性渗透指标(LPI)的HC模型。宋琨等[20]提出了一种基于岩石质量指标(RQD)、岩石渗透性指标(LPD)、裂隙宽度指标(AD)、岩体完整性指标(RID)的RMP模型。陈君等[21]提出了一种基于埋深(Z)、岩石质量指标(RQD)和充填物指标(FSD)的ZRF模型。
前人提出的方法为野外快速、便捷地获取渗透系数提供了重要的依据。但是,有的模型仅考虑了深度或者岩石质量指标单个因素;有的模型虽然综合考虑多种因素,但是在参数选取方面不够灵活,而且实际拟合效果有待提高。因此,现有的估算模型作为野外获取渗透系数的通用模型有一定的局限性。在实际应用中,不同地区的地质条件差异较大,在工程实践中获得的参数亦不尽相同。现有的渗透系数估算模型参数固定、适用性差。因此,建立一种参数选取灵活、准确性高的渗透系数估算模型很有必要。
本文通过对公开数据的整理与分析,提出了一种基于相关性指标的PNC模型。该模型在参数选取方面比较灵活,可以利用现场可获取的参数,选择合理的正、负相关性参数进行拟合,是一种指标选取灵活的渗透系数估算模型。该方法可以为现场条件下快速估算渗透系数提供一种计算依据。
1 渗透系数估算模型
1.1 现有估算模型
现有的渗透系数估算模型,主要分为两种类型。一种是基于单因子估算,例如,表1所示的利用深度估算渗透系数,蒋小伟等[17]利用岩石质量指标估算不同深度的渗透系数,对大尺度范围的估算具有重要意义。但是,由于场地尺度裂隙的复杂性,裂隙的渗透系数不仅受深度或者岩石质量指标等某一种因素的影响,还受到隙宽、裂隙壁面的粗糙度、裂隙的填充指标和岩石基质的渗透性等多重因素的影响。学者们[18,20−21]提出了复合因子的渗透系数估算模型,见表2。
虽然有学者提出了复合因子模型,但仍需要进一步改进。本文重点对比了Hsu等[18]、宋琨等[20],陈君等[21]提出的复合因子估算模型,分析现有估算模型的局限性。
Hsu等[18]在研究中国台湾中部和南部砂岩地区时,提出了基于岩石质量指标RQD、深度指标DI、泥质含量指标GCD和岩性渗透性指标LPI的HC模型:
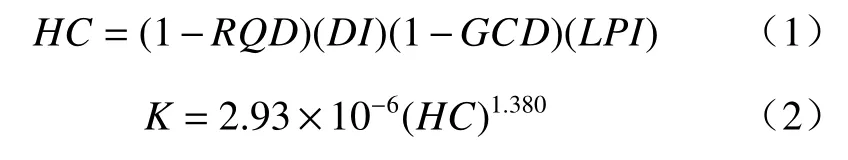

表1 考虑深度Z的渗透系数估算模型Table 1 Estimation model of hydraulic conductivity considering depth Z

表2 复合因子的渗透系数估算模型Table 2 Multi-factor estimation model of hydraulic conductivity

式中:LC——封隔器测试区间中心点的深度;
LT——钻孔的总长度;
K——渗透系数。
实际上,渗透系数的值不会因钻孔的长度而改变。Hsu等[18]选取的两口钻井位于中国台湾的不同地区,钻孔岩芯差异很大。使用HC模型拟合HB-94-01岩芯的渗透系数的效果较好(R2=0.905),但是在拟合HB-95-02时,拟合效果不是很理想(R2=0.495)[21],说明该模型适应性有待提高。
宋琨等[20]研究烟台地下水洞库渗透系数时提出了基于岩石质量指标RQD、岩体完整性指标RID、裂隙宽度指标AD和岩石渗透性指标LPD的RMP模型为:RQD都处理为1(例如ZK204和ZK223),导致最后的渗透系数估算值忽略了充填物指标的影响,主要受到深度的单因素影响。用ZRF模型拟合HB-95-01和HB-95-02的钻孔数据,效果不太理想(图1)。这是因为这两处钻孔的主要地层均为砂岩和泥岩,地应力较大,为8~9 MPa。由RQD可知,该地区岩石较为破碎,导致ZRF估算模型[21]拟合效果不太理想,很难准确地估算该地区渗透系数。
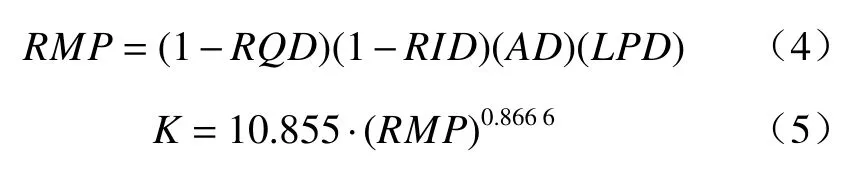
其中,RID是《工程岩体分级标准》(GB 50218—94)[22]中定义的岩体弹性纵波速度与岩石弹性纵波速度之比的平方[22]。但是若实验室测试的岩石弹性纵波速度小于钻孔岩体的弹性纵波速度,会导致RID大于1,这一结果不太合理,所以选取较完整、均质的岩体段作为标准样,采用标准样的最大波速值作为岩石弹性纵波速[20]。这一过程需要人工经验和实验操作判断相结合。人工经验判断存在主观性和不稳定性,难以保证其准确性;而野外现场环境一般不具备实验室操作条件。因此,RMP模型作为一种快速估算岩体渗透系数的通用方法时,具有一定的局限性。
陈君等[21]在对四川省甘孜州雅江县的牙根二级水电站坝体渗透系数的研究中,提出了基于岩石质量指标RQD、充填物指标FSD和深度Z的ZRF估算模型:
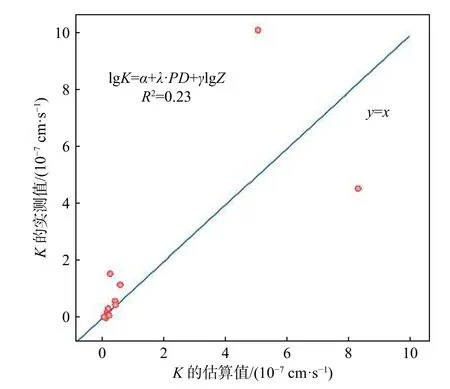
图1 ZRF公式估算的渗透系数与HB-95-01、HB-95-02孔实测K值的拟合结果Fig.1 Fitting results of hydraulic conductivity estimated with the ZRF formula and the measured K values of boreholes HB-95-01 and HB-95-02
综上所述,以往的渗透系数估算模型主要存在两方面问题:(1)部分模型只考虑单因子影响,而岩体渗透系数的影响因素较为复杂,仅靠某一种因子计算求解渗透系数过于粗略;(2)复合因子的模型存在参数选取不够灵活,公式构建不够合理的问题,导致在一些地区进行数据拟合时,效果不够理想。因此,需要提出一种基于复合因子、指标选取灵活、拟合效果较好的岩体渗透系数估算模型。
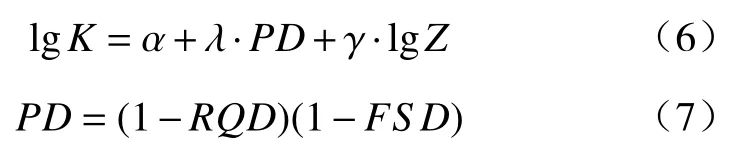
该模型参数的获取方式相较前两种模型较为便捷。但是陈君等[21]在数据处理的过程中将大部分的
1.2 建立正负相关指标的渗透系数估算模型
本文在Hsu等[18]、宋琨等[20]、陈君等[21]对渗透系数估算模型研究的基础上,总结提出了一种基于正、负相关指标的开放型渗透系数估算模型。以前学者采用的复合因子主要有:HC模型中的岩石质量指标、深度指标、泥质含量指标、岩性渗透性指标;RMP模型中提出岩体完整性指标、岩石渗透性指标、裂隙宽度指标;ZRF模型中的岩体充填物指标。并将对这些影响因子进行正、负相关性归类分析,构建出新的拟合模型。
1.2.1 负相关指标(KN)
渗透系数负相关指标,主要是指对渗透系数起负影响作用的参数。例如,岩石质量指标(RQD)是作为评价岩体破损程度的一个重要指标,得到了工程界的普遍认可和广泛应用[23-25]。RQD的计算公式为:

式中:HL——完整岩芯大于10 cm的长度总和;
HT——岩芯的总长。
RQD值越大,完整岩体在总岩体中占比越大。前人[17,26−28]研究RQD与渗透系数K的关系见表3。RQD与渗透系数K之间呈现负相关,即RQD越大,岩体的渗透系数K越小。因此,可以将RQD作为渗透系数的负相关指标。

表3 岩石质量指标RQD与渗透系数K的拟合方程Table 3 Fitting equations of RQD and hydraulic conductivity K
RID是通过岩体纵波速度指数反映岩体完整性指标的参数,RID的计算公式为:

式中:Vm——岩体弹性纵波速/(m·s−1);
Vn——岩石弹性纵波速/(m·s−1)。
RID值越大,表示岩石的完整性越好,岩体的渗透系数随之降低。因此,推断RID与渗透系数K应该呈现负相关,从而可以将RID作为渗透系数的负相关指标。
深度是影响渗透系数的重要指标,已有学者发现渗透系数随深度的增加而衰减的规律[29],因此,深度可以作为影响渗透系数的负相关指标。
1.2.2 正相关指标(KP)
渗透系数的正相关指标,主要是指对渗透系数起正影响的参数。岩性渗透指标LPI[18]和岩石渗透性指标LPD[20]反映渗透性的基本参数,其数值越大,渗透性越好。因此,这两项可以作为正相关指标。
裂隙宽度可以用裂隙宽度指标AD表征:

式中:LF——计算段内裂隙宽度之和/m;
LT——计算段总长/m。
AD越大,岩体中的空隙越大,渗透性越好,故此项可以作为渗透系数的正相关指标。
泥质含量指标GCD和岩体的充填物指标FSD,表示岩体被填充的情况,最大值为1。在文献中使用(1-GCD)[18−19]和(1-FSD)[21]表示,即(1-GCD)和(1-FSD)数值越大代表未被填充的越多,岩体中空隙越大,渗透性越好,故这两项可以作为渗透系数的正相关指标。
1.2.3 改进的渗透系数估算模型
对上述参数进行正、负相关性分类后,提出一种基于正、负相关指标的渗透系数估算PNC模型:
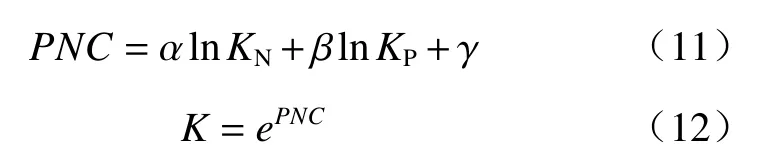
式中:K——估算的渗透系数;
α、β、γ——经验参数;
KN、KP——负相关参数的乘积和正相关参数的乘积。
Hsu等[18]的研究中,KN为负相关指标RQD和Z的乘积,KP为正相关指标(1-GCD)和LPI的乘积。
本模型充分考虑了对渗透系数产生影响的各因素,并且在参数选择上更加灵活。以往研究提出的复合因子模型,大多只是将几组数据进行简单相乘,并未进行分类,导致拟合的效果不够理想。本模型将所有参数进行汇总、评估、分类,分为正、负相关指标,最后采用自然对数进行拟合,得到的公式拟合效果更好。
为了保证估算渗透系数的准确性,正、负相关指标至少需要测试一项。此外,估算模型中的α、β、γ作为经验参数,与岩性、裂隙发育程度等相关。在实际应用中,可以先用尽可能多的正、负相关指标数据进行拟合,求出相应的α、β、γ,然后再将这些参数用于该场地类似条件下岩体渗透系数的估算。
1.3 纳什效率系数
纳什效率系数(NSE)一般用于验证水文模型模拟结果,是水文学中应用最广泛的误差函数之一[30-31]。本文用NSE作为评价模型方法,进一步验证PNC模型的可靠性:
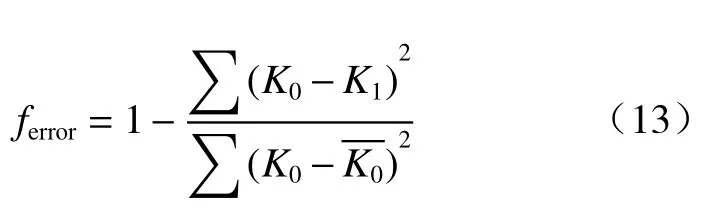
式中:K0——渗透系数的实测值;
——渗透系数实测值的平均值;
K1——渗透系数的估算值;
ferror——误差系数,其值越接近1代表拟合结果越好。
2 模型评估
为了评估PNC模型的拟合效果,本文按照研究区不同岩性进行划分,对Hsu等[18]、宋琨等[20]和陈君等[21]文中的数据进行拟合,并与原文的拟合结果进行对比。
2.1 模型评估一(以Hsu等[18]研究区的数据为例)
文献[18]中的HB-94-01、HB-95-01和HB-95-02钻孔位于中国台湾中部的砂岩和粉砂岩地区。对3口钻孔的数据按照正、负相关指标的思路进行分类整理,结果见表4。值得注意的是,参考文献[20]中的处理方法,将RQD、1-GCD和LPI等于1的值取为0.999,其主要目的是为了防止估算模型中某一项数值为0,避免因未能充分考虑所有影响因素而得到不够精确的结果。此处使用PNC模型拟合3口钻孔渗透系数,并将得到的结果与原文提出的HC模型进行对比分析,拟合对比结果见表4。因为HB-95-01钻孔数据只有3组,故将该钻孔和地理位置相近的HB-95-02钻孔一并拟合分析。
结果显示,PNC模型在拟合Hsu等[18]研究区的钻孔岩性渗透系数方面拟合效果(R2=0.964和R2=0.801)均优于原文的HC模型的拟合效果(R2=0.905和R2=0.563),说明PNC模型在该砂岩地区具有较好的适用性。
2.2 模型评估二(以宋琨等[20]研究区的数据为例)
文献[20]中ZK10钻孔位于山东烟台地下水封洞库的花岗岩地区,对该钻孔的数据按照正、负相关指标的分类思路进行整理(表5)。此处用PNC模型拟合ZK10钻孔的数据,并与原文的RMP模型进行对比,结果见表5。PNC模型在拟合宋琨等[20]研究区的数据时表现出了更好的拟合效果(R2=0.959),优于原文的RMP模型的拟合效果(R2=0.927),表明PNC模型在该花岗岩地区具有较强的适用性。

表4 HB-94-01、HB-95-01和HB-95-02相关数据的分类整理与渗透系数拟合Table 4 Classification of relevant data of borehole HB-95-01,HB-95-01 and HB-95-02
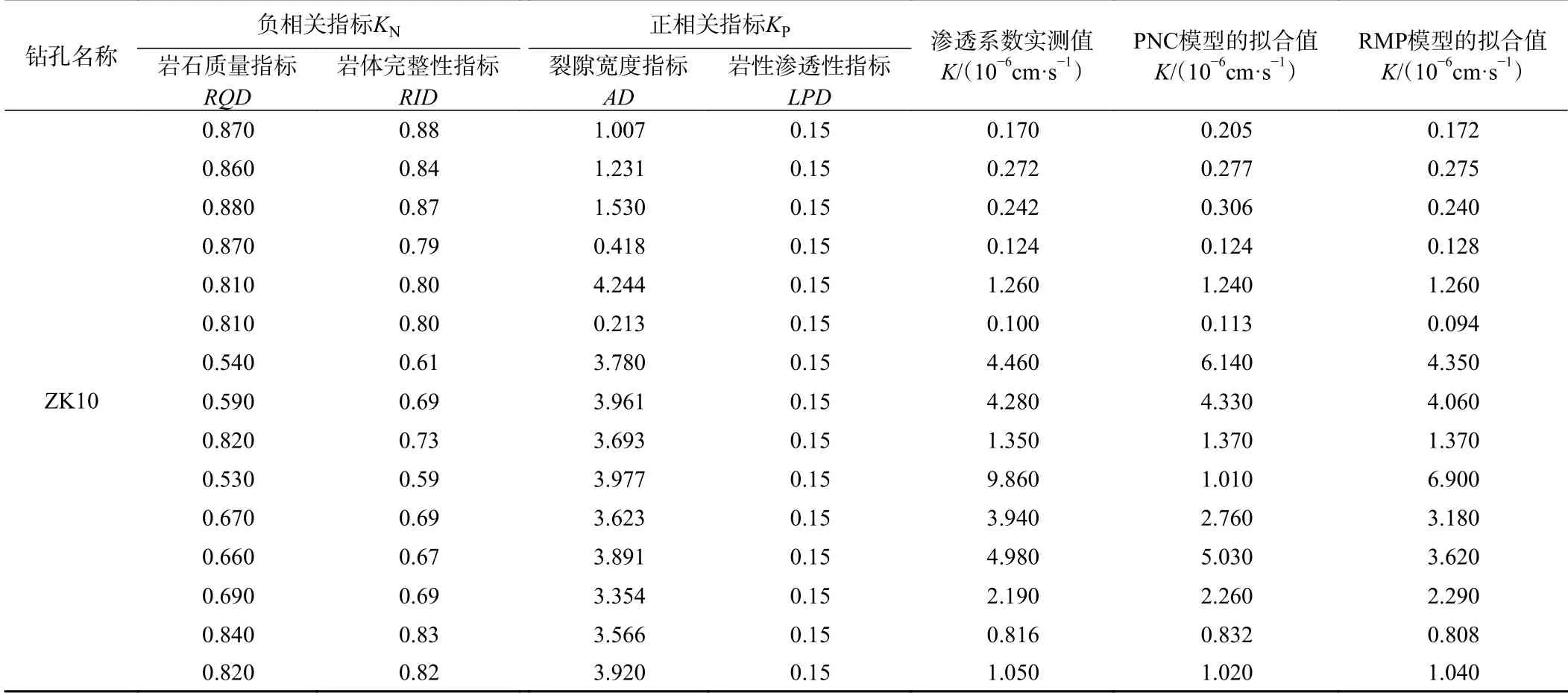
表5 ZK10相关数据的分类整理与渗透系数拟合Table 5 Classification of relevant data and hydraulic conductivity fitting of borehole ZK10
2.3 模型评估三(以陈君等[21]研究区的数据为例)
文献[21]中的ZK343、ZK204、ZK223和ZK153钻孔位于四川牙根二级水电站的花岗岩地区,按照正、负相关指标的分类思路整理4口钻井的数据,将RQD和Z归为负相关指标,(1-FSD)归为正相关指标。此处用PNC公式进行拟合,并与原文提出的ZRF模型拟合效果进行对比分析,结果见表6。由表6可知PNC模型拟合结果相较于ZRF模型效果更好,而且拟合效果都达到R2=0.9以上,说明PNC模型在岩石较为完整的花岗岩地区具有较好的适用性。
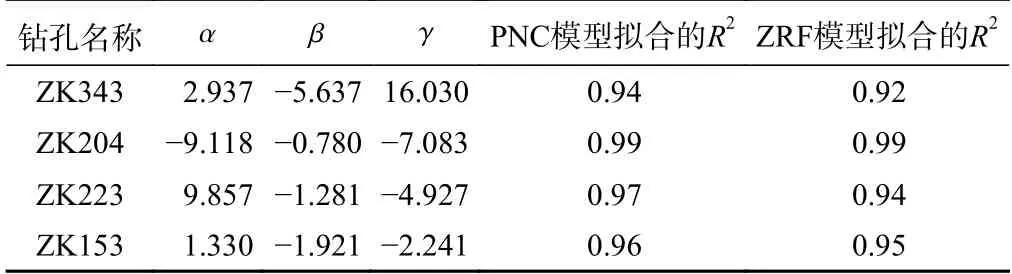
表6 PNC模型与ZRF模型拟合结果对比Table 6 Comparison of the fitting results between the PNC model and the ZRF model

表7 纳什效率系数误差分析Table 7 The NSE error analyses
2.4 模型的误差分析
为了进一步评估PNC模型的准确性,对以上7组数据利用纳什效率系数进行误差分析,结果见表7。通过纳什效率系数的误差分析可知,7组数据中有5组数据的ferror都在0.95以上,说明PNC模型对以上三个地区的数据都表现出了较好的拟合效果。同时,文中提到的8个钻孔(分为7组,其中HB-95-01和HB-95-02合为一组)拟合的可决系数R2均大于0.8,且R2≥0.95占71%,进一步说明了PNC模型拟合效果较好。
3 结论
(1)PNC模型是一种基于正、负相关指标的复合因子模型。该模型作为一种参数开放型的模型,在指标选取方面灵活性较高,应用便捷。
(2)采用PNC模型对7组钻孔岩性的渗透系数进行拟合,结果显示PNC模型拟合的R2均大于0.8,并且拟合R2大于0.95的占71%。对比原作者的估算模型发现,PNC模型表现出较好的拟合效果,并且在常见的砂岩和花岗岩地区中具有较好的适用性。同时,利用NSE进行误差分析,说明PNC模型在估算和验证渗透系数方面具有一定的实际工程应用价值。
(3)PNC为参数开放型模型,本文采用验证模型的钻孔数据量和参数量有限。建议在实际应用中选取尽可能多的参数作为PNC模型的组成部分,使结果可以涵盖多方面因素的影响。另外α,β,γ为不确定参数,需要利用尽可能多的钻孔数据拟合获得,从而提高渗透系数估值的准确性。
