利用生产井监测地下水动态数据处理研究
2021-05-25薛明霞杨晓俊
薛明霞 孙 明 杜 琦 杨晓俊
(山西省水文水资源勘测局太谷均衡实验站 山西太谷030800)
地下水动态监测的目的是为地下水资源开发、利用、保护、管理等提供科学依据。为达到监测的时效性、空间分布的科学性,在专用监测工程不能满足的情况下选用生产井代用。生产井由于抽水干扰,人为地造成瞬时、大幅度的水位波动,使监测数据失真。因此,需要对生产井监测数据进行处理,使其具有较好的代表性。
1 实验监测井布设及监测频率
为了达到实验对比监测的目的,在7.72 km2的实验区域内布设10 眼地下水监测井[1],其中7 眼专用井(编号1~7 号)、3 眼生产井(编号8~10 号)。实验区域为纯井灌区,地下水开发强度较高,农业生产井密度为9 眼/km2,地下水开采模数为30 万m3/a·km2。所有监测井监测频率均为日6 段制(间隔4 h),全自动采集、无线传输、自动接收储存信息。
2 监测井数据变化特征
2.1 专用井数据变化特征
对7 眼专用井2017-2019年地下水动态监测数据进行分析,地下水埋深过程线均呈“V”字型,年内最小值出现在3月中下旬,年内最大值出现在7月份,年变幅较大,在2~10 m 之间,年末差呈下降趋势,为侧向补给-开采型地下水动态类型。地下水位上升期、恢复期大约8 个月,强排泄(主要是开采)下降期4 个月,动态曲线变化特征显著。专用井2017-2019年地下水埋深过程线(以2 号、7 号井为例)见图1、图2;地下水埋深特征值(以2 号井为例)见表1;不同时期(上升期、下降期、恢复期)时段变差(指相邻两次采集信息水位差值)的平均值(时段平均变差)以及地下水位变化特征值(以2 号井为例)见表2。
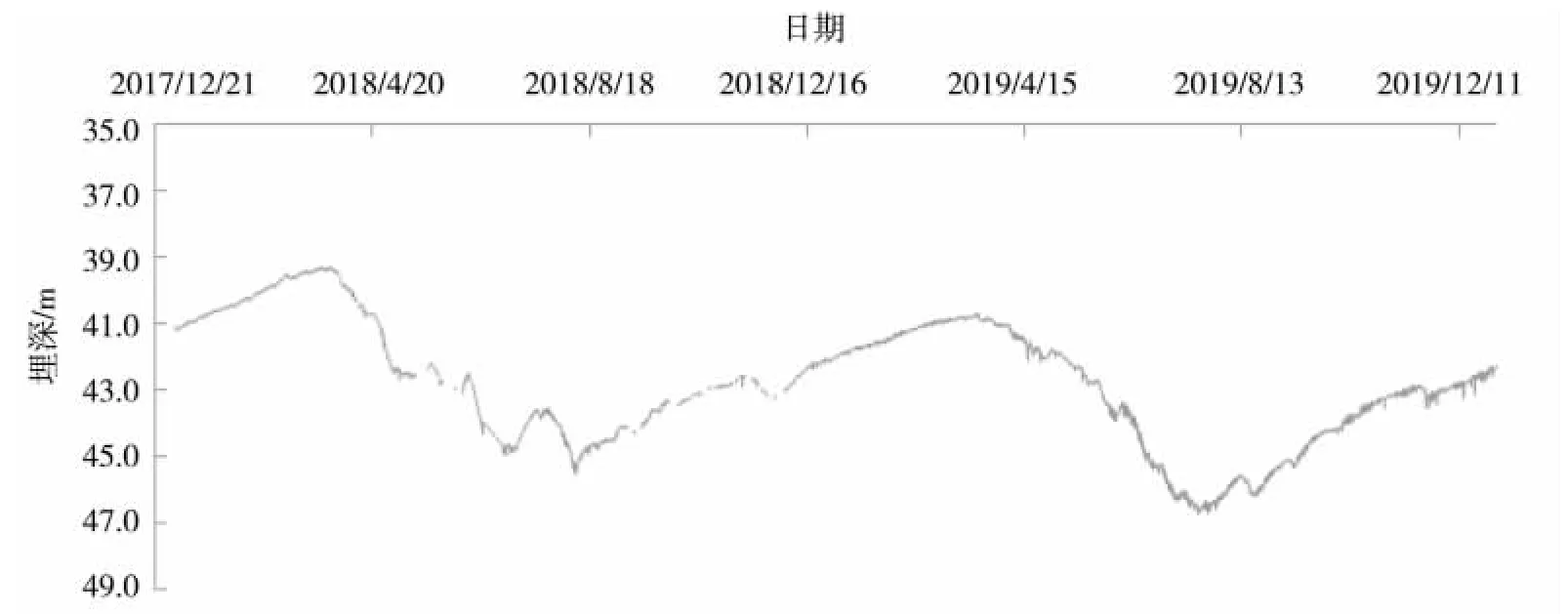
图1 2 号井2018-2019年地下水埋深过程线
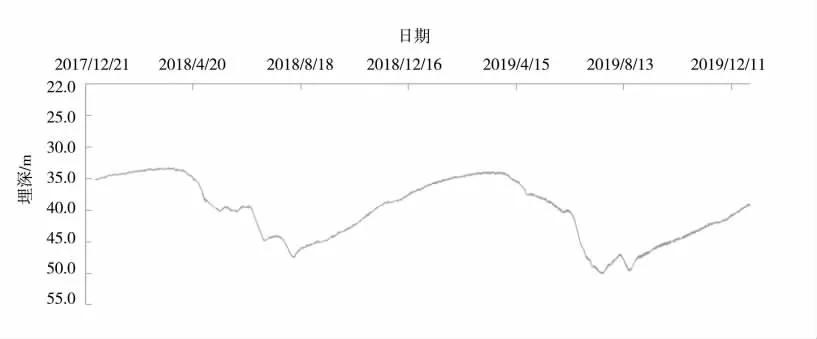
图2 7 号井2018-2019年地下水埋深过程线

表1 2 号井2017-2019年地下水埋深特征值表
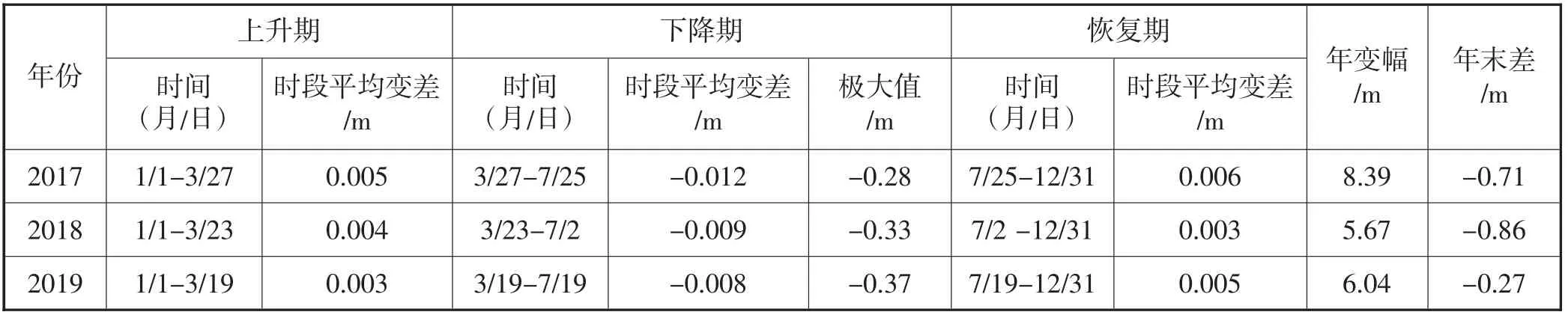
表2 2 号井2017-2019年地下水埋深变化特征表
在高频率监测过程中(日6 段制),地下水位动态过程线呈0~0.5 m 小幅波动,由时段放大可呈明显的震荡过程(以2 号井为例),见图3。
2.2 生产井数据变化特征
对生产井2017-2019年地下水动态监测数据进行分析,其过程线的形状,上升、恢复、下降期的过程均与专用井具有同步性。在高频率监测过程中(日6段制),地下水位动态过程线呈5~15 m 大幅波动,且下降期震荡频率大于恢复期的,表现出农业生产需水过程(以8 号井为例),见图4。
由于生产抽水干扰,生产井地下水位的大幅度波动对区域地下水动态分析增加了糟度。
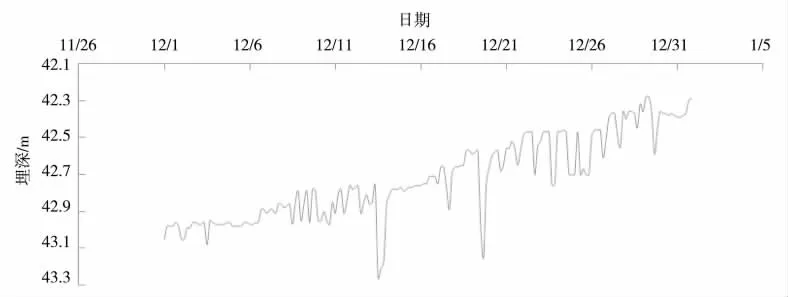
图3 2 号井2019/12/1-2019/12/31 地下水埋深过程线
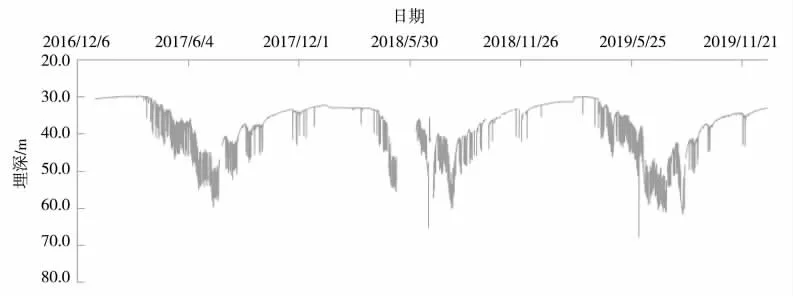
图4 8 号井2017-2019年地下水埋深过程线
3 生产井监测数据处理
虽然生产抽水引起地下水位波动,但由于地下水的流体性质,在停止抽水后,生产井的地下水位在较短时间内得到恢复,与区域水位平衡,趋于区域水位。
地下水因抽水水位下降、停止抽水水位恢复的变动过程与地下水监测信息采集定时点是随机事件,发生在水位“V”字型变化的不同位置,两次采集信息水位变差0~9 m,远大于区域专用井两次采集信息水位变差0~0.5 m,因此要滤除生产井地下水位因抽水引起的随机干扰。
3.1 监测数据处理方法
为滤除采集到的地下水位信息中的干扰信息,提高信息的准确性和稳定性,一般采用数字滤波法[2,3,4]。
本文选择限幅平均滤波法滤除采集到的地下水位信息中的干扰信息。
限幅平均滤波法是“限幅滤波法”与“递推平均滤波法”的组合,即对采集信息先进行限幅滤波处理,再进行递推平均滤波处理。
限幅滤波法又称程序判断滤波法,是处理随机干扰的一种有效方法。基本步骤为:比较相邻两个时刻n和n-1 对应的两个采样值y(n)和y(n-1),根据经验确定两次采样允许的最大偏差。如果两次采样值的差值超过允许的最大偏差范围,则认为发生随机干扰,且后一次采样值y(n)为非法值,予以删除,并用y(n-1)代替y(n);如果未超过允许的最大偏差范围,则认为本次采样值有效。限幅滤波法能有效消除偶然出现的脉冲干扰,但无法抑制周期性的干扰,平滑度差。
递推平均滤波法是将连续N 次采样的数据看成一个队列,每更新一次数据,去掉队首的数据,将更新的数据放在队尾,即队列的长度固定为N。再将更新后得到的N 个数据进行算术平均,用算术平均值替代本次更新的数据,从而得到有效的滤波数据。递推平均滤波法对周期性干扰有良好的抑制作用,平滑度高,适用于高频振荡的系统,但对偶然出现的脉冲性干扰的抑制作用较差。
限幅平均滤波法融合了两种滤波法的优点。对于偶然出现的脉冲干扰,可消除由于脉冲干扰所引起的采样值偏差,并对周期性干扰有良好的抑制作用,平滑度高。
3.2 限幅滤波法
3.2.1 限幅滤波参数寻优
限幅滤波时,首先要根据经验确定相邻两次采样允许的最大偏差,即确定最优滤波参数。根据地下水位变化特征(表2),专用井地下水位上升期和恢复期的时段平均变差较小,下降期的时段平均变差(绝对值)最大。分析生产井的时段变差,计算不同时段变差范围对应的时段平均变差,寻找时段平均变差(绝对值)最接近专用井下降期时段平均变差(绝对值)时对应的时段变差范围,此时段变差范围即为生产井相邻两次采样允许的最大偏差,即最优滤波参数。以8 号井为例进行分析。8 号井2017-2019年共有6 569 个时段,时段变差在-27.82~27.78 m 之间,将时段变差划分为不同时段变差范围,计算其对应的时段平均变差,计算结果见表3。表3 中,8 号井的时段平均变差(绝对值)均大于专用井下降期时段平均变差(绝对值),时段变差范围为-2.5 m≤ΔH≤2 m(ΔH 表示时段变差)时的时段平均变差(绝对值)最接近专用井下降期时段平均变差(绝对值),且时段数占总时段数的87.46%,具有很好的代表性。因此,利用时段变差范围-2.5 m≤ΔH≤2 m 确定最优滤波参数即两次采样允许的最大偏差值。当ΔH>0,表示地下水埋深减小,地下水位上升,最优滤波参数即两次采样允许的最大偏差值为2 m;当ΔH<0,表示地下水埋深增加,地下水位下降,最优滤波参数即两次采样允许的最大偏差值为-2.5 m。
3.2.2 限幅滤波
根据确定的最优滤波参数,对生产井监测数据进行限幅滤波处理。以8 号井为例进行分析。8 号井2019年11月22日8 时,地下水埋深值为34.67 m,12时为42.93 m,即相邻两个时刻n 和n-1 为n=12,n-1=8。y(n-1)=y(8)=34.67 m,y(n)=y(12)=42.93 m,ΔH=y(n-1)-y(n)=y(8)-y(12)=34.67-42.93=-8.26 m,ΔH<0且ΔH<-2.5 m,因此认为y(n)=y(12)=42.39 m为非法值,予以删除,并用y(n-1)=y(8)=34.67 m 代替,y(n)=y(12)= y(n-1)=y(8)=34.67 m,即滤波后,12 时的地下水埋深值为34.67 m。继续判断下一时刻,11月22日16 时地下水埋深值为35.55 m,相邻两个时刻n和n-1 为n=16,n-1=12。此时,y(n-1)=y(12)=34.67 m,y(n)=y(16)=35.55 m,ΔH= y(n-1)-y(n)=y(12)-y(16)=34.67-35.55=-0.88 m,ΔH <0 但ΔH >-2.5 m,因此认为y(n)=y(16)=35.55 m 为有效值,予以保留,即滤波后,16 时的地下水埋深值仍为35.55 m。
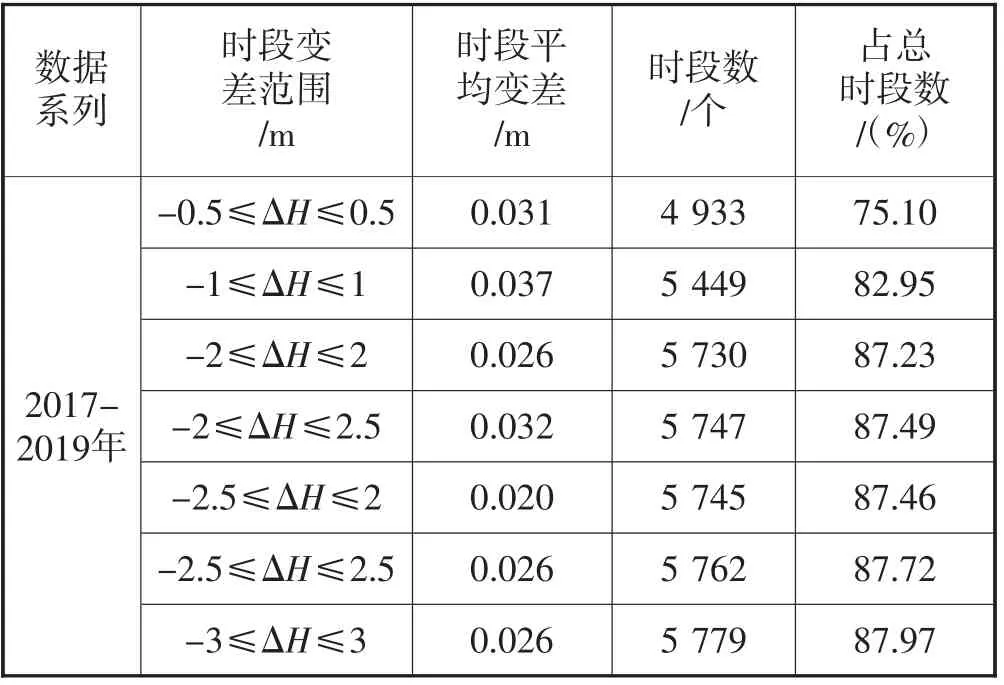
表3 8 号井地下水位时段变差表
限幅滤波法滤波结果(以8 号井为例)见图5。
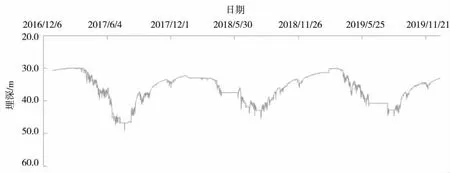
图5 8 号井2017-2019年地下水埋深过程线
3.3 递推平均滤波法
3.3.1 递推平均滤波参数寻优
递推平均滤波法递推队列的长度设定随意性较大,既要满足数据的敏感性还要达到平滑性,并保持数据发展的趋势性,结合地下水位变化特征,选择递推队列的长度为日监测频次+1。地下水监测井日监测频次为6 次,则递推队列的长度N=6+1=7。
3.3.2 递推平均滤波
根据确定的递推队列长度,对生产井限幅滤波处理后的数据进行递推平均滤波处理。以8 号井为例进行分析。8 号井2019年1月1-2日的地下水位限幅滤波数据见表4。将2日0:00 的限幅滤波数据作为更新数据,递推队列长度N=7,则递推队列由1日0:00、4:00、8:00、12:00、16:00、20:00 的6 次限幅滤波数据与2日0:00 的限幅滤波数据组成—32.14+32.14+32.13+32.13+32.05+32.13+32.12,其平均值为32.12 m,则2日0:00 递推平均滤波后的数据为32.12 m。再将2日4:00 的限幅滤波数据作为更新数据,则递推队列由1日4:00、8:00、12:00、16:00、20:00 的5 次限幅滤波数据与2日0:00 递推平均滤波后的限幅平均滤波数据以及2日4:00 的限幅滤波数据组成—32.14+32.13+32.13+32.05+32.13+32.12+32.06,其平均值为32.11 m,则2日4:00 递推平均滤波后的数据为32.11 m。依次类推,得到2日各数据对应的限幅平均滤波数据。见表4。
递推平均滤波法滤波结果(以8 号井为例)见图6。

表4 8 号井2019年1月1-2日地下水位数据表
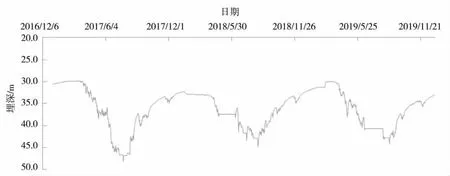
图6 8 号井2017-2019年地下水埋深过程线
4 成果与分析
由于3 眼生产井属于同一实验区域,生产抽水引起地下水位波动具有相似性,因此,8 号井的限幅滤波最优滤波参数分析结果同样适用于9 号井和10号井。

图7 9 号井2017-2019年地下水埋深过程线
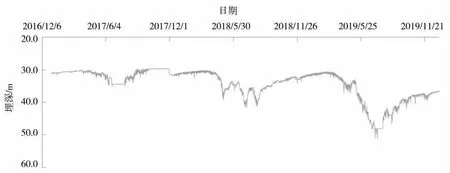
图8 9 号井2017-2019年地下水埋深过程线
利用限幅平均滤波法对3 个生产井2017-2019年的地下水动态监测数据进行滤波,8 号井滤波前后对比结果见图4~图6、9 号井滤波前后对比结果见图7~图9、10 号井滤波前后对比结果见图10~图12。
由图6、图9、图12 和图1、图2 的对比可以看出,经过限幅平均滤波法滤除采集到的地下水位信息中的干扰信息,生产井与专用井具有相同的地下水动态曲线变化特征,可以与专用井一起参与区域地下水位动态分析,为区域地下水资源开发利用、保护管理等提供科学依据。
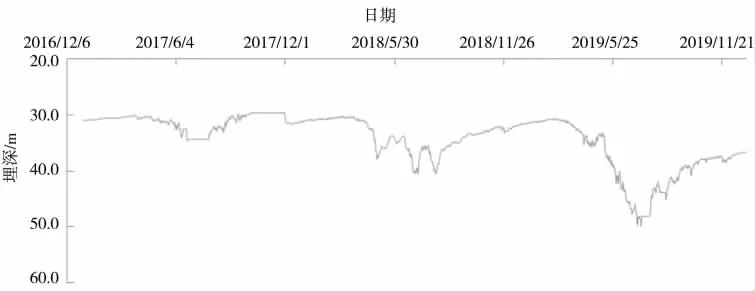
图9 9 号井2017-2019年地下水埋深过程线

图10 10 号井2017-2019年地下水埋深过程线
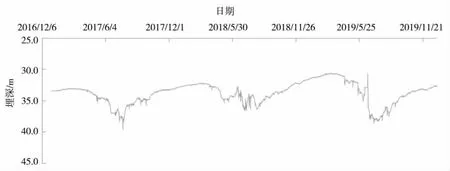
图11 10 号井2017-2019年地下水埋深过程线
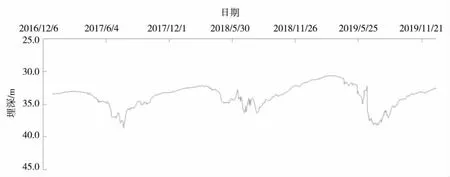
图12 10 号井2017-2019年地下水埋深过程线
5 结论
利用生产井监测地下水动态数据,受抽水干扰等人为因素影响,数据波动较大,通过对地下水动态过程分析以及数字滤波法的研究,提出了限幅平均滤波法,其中,限幅滤波法能够有效去除人为干扰造成的大幅波动,递推平均滤波法能够很好的抑制周期性的干扰,保证数据发展的趋势性。
考虑到滤波参数对滤波效果的影响,根据地下水动态变化特征,进行了滤波参数寻优,限幅滤波法最优滤波参数在地下水埋深减小,地下水位上升期为2 m;在地下水埋深增加,地下水位下降期为-2.5 m。递推平均滤波法递推队列的长度为监测井日监测频次+1。经限幅平均滤波法处理,生产井监测数据能够满足区域分析需求。
