海底山脊作用下内孤立波破碎研究*

林颖典 余俊扬 罗辕野 袁野平

海底山脊作用下内孤立波破碎研究*

林颖典 余俊扬 罗辕野 袁野平①

(浙江大学海洋学院 舟山 316000)

基于实验室水槽实验, 研究了内孤立波在海底山脊地形存在下的破碎过程。实验设置了两层流体的分层环境, 定量地控制了上下层水体厚度及密度, 使用不同高度的高斯地形模拟实际的海山作用, 讨论了不同高度地形作用下内孤立波破碎过程的异同。实验结果表明, 内孤立波的破碎过程中由于逆压梯度的存在, 在地形处发生边界层分离, 产生了底边界层反向射流和涡脱落现象, 计算了内孤立波破碎过程中产生的底部切应力的分布。本文通过实验模拟了内孤立波再海山作用下的破碎过程, 进一步探究了海山对内孤立波破碎的影响和底部切应力的作用, 对于研究自然界中海洋内孤立波在海山区域的破碎现象有参考价值。

内孤立波; 内波破碎; 边界层分离; 底床切应力

内波是发生在密度稳定层化流体内部的一种波动现象, 其中内孤立波(internal solitary waves, ISWs)是内波的一种。目前普遍认为内孤立波主要由正压潮与地形(如海峡, 海山等)的相互作用产生的内潮波在传播过程中逐渐裂变而成(方欣华等, 2005; 王金虎等, 2016)。与内潮波相比, 它具有强非线性与大振幅的特点(蒋国荣等, 2005); 与表面波相比, 内孤立波在水深为无穷大时依然可以存在(Davis, 1967)。内孤立波对全球海洋中的动量、能量和物质交换起到促进作用, 且对当地海域的水动力过程有显著影响(Klymak, 2012)。有研究指出, 内波的破碎是内波能量耗散的主要途径之一(杜涛等, 2001)。Ledwell等(2000)发现内波在经过海底地形时会发生变形并破碎, 产生大尺度湍流, 造成强烈剪切作用, 加剧了水体在垂向上的混合。内波发生破碎后, 密度跃层附近的水体流速梯度极大, 强烈的剪切作用会威胁到海上平台 (刘国涛等, 2007)。

我国南海北部区域是全球内波最为频发的海域(Alford, 2015; 梁辉等, 2016), 观测记录显示南海内孤立波具有较大振幅 (Lien, 2014; Li, 2016), 其中观测记录中最大的内孤立波有约240 m的振幅(Huang, 2016)。Alford等(2015)结合观测结果与数值模型分析了南海北部的破碎情况, 认为大振幅内波的破碎显著增强了海域内的湍流强度。Jia等(2019)通过对南海北部内波与悬浮泥沙分布的观测, 研究了内孤立波活动对底边界泥沙再悬浮的影响。Vlasenko等(2010)使用完全非线性非流体静力学模型首次模拟了南海北部内波的生成过程, 并展现了吕宋海峡的两座山脊之间的更多细节。张善武等(2015)运用变系数eKdV 方程数值求解中国南海大振幅内孤立波的振幅和波宽等特征参数。Zeng等(2019)基于实际地形和潮汐情况建立了南海北部内波的三维数值模型, 研究了南海北部内波的生成和传播过程。

数值模拟是研究内孤立波破碎过程的一种方便有效的方法, 已有的研究针对内孤立波在斜坡、三角、圆角及高斯地形上的破碎过程进行了模拟和分析。Vlasenko等(2002)在使用雷诺平均的Navier- Stokes方程, 模拟出了完整的内孤立波破碎过程, 结果表明随着水深变浅, 内孤立波会由于运动过程中的不稳定性而破碎, 破碎后的下层水体以类似异重流的方式继续向岸传播。Aghsaee等(2015)使用高精度二维直接数值模拟(direct numerical simulation, DNS), 模拟了内孤立波在缓坡地形上发生变形到破碎的过程, 其结果表明底边界的涡脱落现象与逆压梯度及分离流雷诺数有关, 这类不稳定性是造成泥沙再悬浮的重要原因。Harnanan等(2015)模拟了凹陷型内孤立波在平缓的底部地形上的运动过程, 发现了一种与边界层反向射流相关的不稳定, 并导致涡脱落。

在物理实验研究中, 近年来粒子图像测速技术(particle image velocimetry, PIV)及声学多普勒流速仪(acoustic doppler velocimetry, ADV)成为了主要流速测量方法, 也被广泛用于内孤立波的相关实验研究中。Carr等(2006, 2008)使用ADV方法进行流速测量, 发现内孤立波在浅水中传播过程中会引起底边界的全局不稳定性, 并发展为底边界射流。Boegman等(2009)使用PIV技术捕捉到了内孤立波在斜坡破碎时在底边界引起的向上流, 并总结了内波从变形、破碎到引起泥沙再悬浮的过程。Sutherland等(2013)将在斜坡地形上破碎的内波以坡度与波陡之比来加以分类。黄鹏起等(2016)研究了内孤立波在缓坡地形上的破碎, 并计算了内波破碎时的湍动能耗散率, 他们发现实验室实验中湍动能耗散率的量级相比实地观测所测得的大一个数量级。Mu等(2019)研究了内孤立波在一个三角形障碍物上破碎的过程, 并总结了湍动能耗散率随着内孤立波振幅变化的规律。

上述的研究对于地形作用下的内孤立波破碎现象及破碎机制进行了有启发意义的探讨, 但是内孤立波破碎过程中的边界层分离以及涡产生机制仍然缺乏详尽系统的研究。本文通过实验室实验方法, 系统地研究了在不同高度的高斯形地形影响下的内孤立波破碎过程, 并通过PIV技术获得破碎过程的流场数据, 分析内孤立波破碎的动力机制, 为内孤立波破碎的理论研究、数值模拟及实地观测提供重要的参考及依据。

1 研究方法

1.1 实验装置与步骤

本实验在浙江大学海洋学院地球物理海洋实验室的内波水槽中进行。实验装置如图1所示, 水槽尺寸为10 m×0.16 m×0.36 m, 水槽左侧的平板型进水口与两个重力式水箱相连, 分别装有1=1.030 g/cm3与2= 1.050 g/cm3两种密度的盐水, 水槽的右端为一个斜坡多孔板型的消波装置。在水槽前方放置的CCD(charge coupled device)相机正对水槽进行拍摄, 其分辨率为2592×2048 pixels, 拍摄频率为40 帧/s, 实际所得图像的空间分辨率为0.034 cm/pixel, 时间分辨率为0.025 s/帧。水槽上方固定两个激光发射器, 发射波长为532 nm激光片光源, 片光厚度约为3 mm。在所有实验进行过程中, 实验室维持恒温在23 ºC左右。

图1 实验装置示意图

在配置盐水时, 将直径为20 μm, 密度为1.040 g/cm3的聚苯乙烯粉末掺入其中作为PIV的示踪粒子, 这类粒子满足PIV测速所要求的跟随性并能够基本实现对湍流的测量。在实验开始前需要生成双层流体的密度分层环境, 通过水槽左侧的平板型进水口向水槽内先加入上层密度较小的盐水, 厚度为1=4 cm, 静置一段时间后再通过平板型进水口缓慢地加入下层密度较大的盐水, 直到总水深=1+2=20 cm, 并且要充分静置后才可以开始实验。在内孤立波的实验过程中, 使用重力塌陷造波法(Michallet, 1999)来生成内孤立波, 即向水槽左端插入活动闸门, 通过细橡胶虹吸软管缓慢地向闸门左侧加入上层低密度盐水, 使得双层流体分界面在闸门的两侧产生高度差, 这一高度差被称为塌陷高度, 移除闸门后可产生内孤立波。重力塌陷造波法生成的内孤立波特性主要受塌陷高度和闸室长度影响, 通过改变塌陷高度的方式生成多种振幅的内孤立波, 同时根据经验保持闸室长度为恒定为35 cm, 以保证生成的内孤立波波形完整稳定以及始终只有单个内孤立波。造波过程中不可避免地会产生一些微小振幅的尾波, 由于这些尾波与前导波相距一个波长距离以上, 可以认为这些尾波的作用对内孤立波的破碎过程没有明显的影响, 因此本文的分析中将不重点考虑这一因素。

1.2 特征参数与实验工况

内孤立波的恢复力为重力和浮力的合力, 称之为约化重力, 一般采用有效重力加速度来描述, 定义为

实验中采用高斯形的地形, 其宽度固定为30 cm, 高度共有5种方案, 如表1所示, 并且对每种地形条件都进行了四种塌陷高度的实验, 因此共计有24个实验工况。为方便描述, 我们将不同地形工况下的实验组别记为D1—D5, 分别对应地形高度为5—15 cm的地形工况。表1给出了实验的分组设置和具体参数。

表1 实验工况设置

Tab.1 Experimental settings and parameters

1.3 数据处理

对实验中获得的图像序列使用MATLAB对图像进行预处理, 之后利用基于MATLAB的PIV粒子图像处理软件PIVlab(Thielicke, 2014)分析图像, 从而得到内波的速度场和涡度场数据。PIVlab计算流场的核心算法是基于图像灰度值的互相关匹配算法, 该方法稳定可靠且有足够精度, 本文中选取积分窗口尺寸为32×32 pixel, 空间步长为8 pixel。

式中, 内波的波幅a在地形上游断面测得, 并记录该断面上流体交界面随时间变化。对式(3)进行变量代换, 其中为内孤立波行进的平均速度, 即可计算得到内孤立波的特征波长。

2 实验结果

2.1 速度场与涡度场

本节主要分析对比了各工况下的速度场与涡度场。其中在二维平面上, 涡度计算公式为

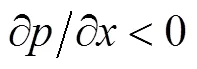
图3 内孤立波破碎过程中涡的产生(a)与脱落(b)

注: 红色虚线圆框表示脱落的涡旋;表示水平方向;表示垂直方向

图4a给出了地形高度较小, 即/1=1.25时流场和涡量场的变化过程。图4a1中, 内孤立波接近地形, 下层流体绕地形流动, 沿着地形坡面边界产生正涡度, 由于地形高度较小, 内波与地形间的相互作用并不强烈, 内孤立波波面形状保持稳定。当波谷传播到地形山脊上方时, 即如图4a2—a3所示, 波后密度跃层前倾突出并最终发生倾覆, 波面产生了Z字型断裂。而在底边界层, 由于内孤立波波后导致的负压梯度, 发生边界层分离, 图4a1—a3中显示了分离涡从产生到脱落的全过程。图4a4中内孤立波已经越过地形, 边界层上的分离涡逐渐变厚, 而后在中心发生横向断裂并产生反向涡, 反向涡脱落并破碎成更小的涡, 此后逐渐耗散最终消失。在整个破碎的过程中, 下层水体的速度通量逐渐降低, 其最大速度发生于边界层分离之前, 如图4b水平流速剖面所示, 这一现象同Carr (2006)所得结论一致, 即速度不是导致边界层分离的主要原因, 内孤立波和地形相互作用引起的逆压梯度区主导了边界层反向射流和分离涡的生成和发展。

图4 工况D1(η0=11 cm)下的速度场、涡度场(a)及水平流速剖面(b)

在地形高度中等,即/1=3.125的情形下(如图5所示), 内波与地形的相互作用效果较为明显。内孤立波遇到地形后导致密度跃层发生明显变形, 如图5a1, 内孤立波前缘锋面趋向于平行于地形迎流坡面, 并进一步贴近坡面, 使得内波前缘和坡面间的间距变得极窄。如图5b, 相比较低地形的情况, 这一区域内流体的流速梯度变得更大。在图5a2中, 随着内波前部越过地形, 在地形中部产生了一个存在较大逆压梯度的区域, 紧接着在地形坡面上发生边界层分离并产生了底部反向射流, 并逐渐延伸至地形顶部。在边界层分离和反向射流的作用下, 在地形前方形成了多个沿坡面切向的正负涡度相间的条带状结构, 如图5a2—a4。与较小地形条件下不同的是, 分离涡未经历最后的增厚过程就被波面与反向射流分割以致脱落, 密度跃层内与上层流体被掺入下层, 导致强烈的混合。

图6显示了地形高度较大/1=3.75的情形。如图6a1所示, 地形顶部与密度跃层相距较近, 当内孤立波传播到地形附近时, 密度跃层向下位移小段距离后就会被地形截断, 因此地形对内波的反射作用更显著。反射波在图6a中用红色虚线方框标出, 内孤立波在地形作用下反向传播, 在这个过程中(如图6b), 下层的水平流速反向, 但是由于上层水体可以正常向右运动, 上层的水平流速明显减小但仍为向右方向。速度的反向、增大在地形上游位置形成湍流, 如图6a3—a4产生一系列正负相间的涡, 同时逐渐向上游位置发展。

图5 工况D4(η0=7 cm)下的速度场、涡度场(a)及水平流速剖面(b)

注: 黑色实线方框代表图7的显示范围

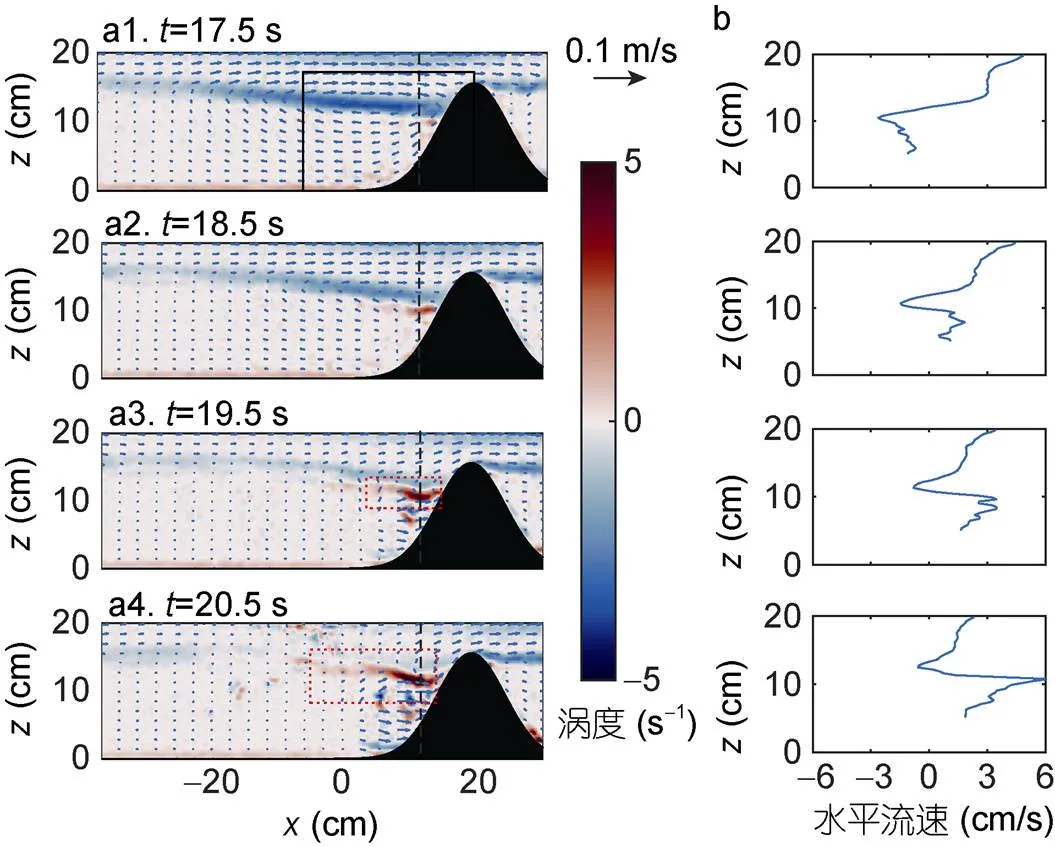
图6 工况D5(η0 = 7 cm)下的速度场、涡度场(a)及水平流速剖面(b)

注: 黑色实线方框代表图7的显示范围, 红色虚线方框代表反射波

2.2 底边界层切应力

图7 D1 (a, b)、D4 (c, d)、D5 (e, f)地形条件下(η0=7 cm)的底部切应力沿着x方向分布及初始时刻对应的局部流场图

D1工况下在内孤立波刚接触山脊地形时, 底部切应力在地形中部区域即=14.5 cm附近突然增大, 如图7a, 这一处恰好是地形局部坡度达到最大值的位置; 而在=20 cm即地形顶部, 切应力迅速减小。如图7b, 在=14 s时, 由于地形局部坡度的影响, 率先在=14.5 cm处发生边界层分离, 在底部产生底边界射流, 并沿着地形坡面向上延伸, 直到接近地形顶部, 地形的局部坡度变化抑制了底边界射流, 底部切应力迅速减小。随着时间的发展, 底边界射流强度与厚度增大, 反应在图中便是切应力峰值逐渐增大, 直至最后发生涡脱落, 此时切应力曲线的上升起点发生前移。中等高度地形D2的切应力基本集中于地形顶部附近, 如图7c, 且随着时间变化其值逐渐增大, 而峰值位置只沿着坡面向上微微偏移。如图7d, 内孤立波与地形相互作用的初始时刻即被激发了强烈的反向射流, 从而导致了涡的产生和切应力的急剧增大, 因而其切应力在最初阶段就明显大于其他地形工况。对于较高地形的情形D3, 由于未产生明显的底边界射流, 如图7e, 底部切应力分布相对均匀并且有双峰形的分布趋势。随着地形的增高增强了对下层流体的阻滞作用, 如图7f, 内波被地形反射造成回流。当内孤立波波幅与地形均较大时, 内孤立波的密度跃层被地形隔断, 阻碍了地形下游侧流体越过地形到另一侧, 地形上的沿坡流由于缺少流体补充而变弱, 结果便是底部切应力的减小。

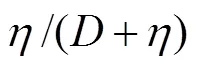
图8 最大切应力随η/(D+η)分布图

3 结论

本文在内波水槽中使用PIV技术对凹陷型内孤立波的传播及破碎进行了观测, 对内孤立波在不同高度的高斯型地形作用下的破碎过程进行了较为详细的研究, 对破碎过程中的流场结构和重要的流动现象进行了分析。

在较小地形, 波面不发生明显变形, 在逆压梯度的影响下, 地形中部产生边界层反向射流, 沿坡向下流的正涡厚度增大, 发生涡脱落并产生耗散。在中等地形上破碎时, 波面发生变形, 产生平行的2条正负涡带, 也在逆压梯度的作用下产生反向射流, 形成3条涡带, 而后2条负涡带将正涡带切割发生整体涡脱落, 负涡带也随之发生断裂, 形成正负相间的涡度分布结构, 期间高耗散率出现在沿坡向下流和涡脱落位置。对于最大的地形, 地形顶峰紧贴密度跃层, 内孤立波波面在地形发生反射, 而上层水通过地形后, 下层水体整体发生回流, 在下层水体中产生大量涡和耗散。同时, 我们考虑了底部切应力的作用, 根据湍动能估算了底床切应力, 发现破碎情况下最大切应力随/()增大近似线性增大, 而内波不发生破碎时, 最大切应力明显小于其他情况。

本文为相关研究提供了重要的实验依据, 并丰富了内波-地形相互作用的理论框架。对于后续的工作, 首先需要考虑更为复杂的地形条件, 例如迎流坡与反坡不对称的地形等; 其次对于内波导致的沿坡流的边界层内流动结构, 需要更高精度的实验或数模手段进行研究, 以揭示底边界层在内波破碎过程中的作用。

王金虎, 陈 旭, 徐 洋, 2016. 粗糙地形对内波生成影响的实验研究. 海洋与湖沼, 47(4): 706—713

方欣华, 杜 涛, 2005. 海洋内波基础和中国海内波. 青岛: 中国海洋大学出版社

刘国涛, 尚晓东, 陈桂英等, 2007. 海洋内波破碎及其能量耗散的研究进展. 中山大学学报(自然科学版), 46(S2): 167—172

杜 涛, 吴 巍, 方欣华, 2001. 海洋内波的产生与分布. 海洋科学, 25(4): 24—28

张善武, 范植松, 石新刚, 2015. 变系数EKdV模型在模拟南海北部大振幅内孤立波传播和裂变中的应用. 中国海洋大学学报, 45(4): 9—17

黄鹏起, 陈 旭, 孟 静等, 2016. 内孤立波破碎所致混合的实验研究. 海洋与湖沼, 47(3): 533—539

梁 辉, 郑 洁, 田纪伟, 2016. 南海西北陆坡区内潮与近惯性内波观测研究. 海洋学报, 38(11): 32—42

蒋国荣, 汪晓娇, 张 军等, 2005. 内波研究的国内外发展现状. 海洋预报, 22(S1): 176—182

Aghsaee P, Boegman L, 2015. Experimental investigation of sediment resuspension beneath internal solitary waves of depression. Journal of Geophysical Research: Oceans, 120(5): 3301—3314

Alford M H, Peacock T, MacKinnon J A, 2015. The formation and fate of internal waves in the South China Sea. Nature, 521(7550): 65—69

Boegman L, Ivey G N, 2009. Flow separation and resuspension beneath shoaling nonlinear internal waves. Journal of Geophysical Research: Oceans, 114(C2): C02018

Carr M, Davies P A, 2006. The motion of an internal solitary wave of depression over a fixed bottom boundary in a shallow, two-layer fluid. Physics of Fluids, 18(1): 016601

Carr M, Davies P A, Shivaram P, 2008. Experimental evidence of internal solitary wave-induced global instability in shallow water benthic boundary layers. Physics of Fluids, 20(6): 066603

Davis R E, Acrivos A, 1967. Solitary internal waves in deep water. Journal of Fluid Mechanics, 29(3): 593—607

Harnanan S, Soontiens N, Stastna M, 2015. Internal wave boundary layer interaction: A novel instability over broad topography. Physics of Fluids, 27(1): 016605

Huang X D, Chen Z H, Zhao W, 2016. An extreme internal solitary wave event observed in the northern South China Sea. Scientific Reports, 6: 30041

Jia Y G, Tian Z C, Shi X F, 2019. Deep-sea sediment resuspension by internal solitary waves in the Northern South China Sea. Scientific Reports, 9: 12137

Klymak J M, Legg S, Alford M H, 2012. The Direct Breaking of Internal Waves at Steep Topography. Oceanography, 25(2): 150—159

Ledwell J R, Montgomery E T, Polzin K L, 2000. Evidence for enhanced mixing over rough topography in the abyssal ocean. Nature, 403(6766): 179—182

Li Q, Wang B, Chen X, 2016. Variability of nonlinear internal waves in the South China Sea affected by the Kuroshio and mesoscale eddies. Journal of Geophysical Research: Oceans, 121(4): 2098—2118

Lien R C, Henyey F, Ma B, 2014. Large-amplitude internal solitary waves observed in the northern South China Sea: properties and energetics. Journal of Physical Oceanography, 44(4): 1095—1115

Michallet H, Ivey G N, 1999. Experiments on mixing due to internal solitary waves breaking on uniform slopes. Journal of Geophysical Research: Oceans, 104(C6): 13467—13477

Mu H D, Chen X, Li Q, 2019. Laboratory experiments on an internal solitary wave over a triangular barrier. Journal of Ocean University of China, 18(5): 1061—1069

Soulsby R L, Dyer K R, 1981. The form of the near-bed velocity profile in a tidally accelerating flow. Journal of Geophysical Research: Oceans, 86(C9): 8067—8074

Sutherland B R, Barrett K J, Ivey G N, 2013. Shoaling internal solitary waves. Journal of Geophysical Research: Oceans, 118(9): 4111—4124

Thielicke W, Stamhuis E J, 2014. PIVlab—towards user- friendly, affordable and accurate digital particle image velocimetry in MATLAB. Journal of Open Research Software, 2(1): e30

Vlasenko V, Hutter K, 2002. Numerical experiments on the breaking of solitary internal waves over a slope–shelf topography. Journal of Physical Oceanography, 32(6): 1779—1793

Vlasenko V, Stashchuk N, Guo C, 2010. Multimodal structure of baroclinic tides in the South China Sea. Nonlinear Processes in Geophysics, 17(5): 529—543

Zeng Z, Chen X E, Yuan C X, 2019. A numerical study of generation and propagation of type-A and type-B internal solitary waves in the northern South China Sea. Acta Oceanologica Sinica, 38(11): 20—30

EXPERIMENTAL STUDY ON INTERNAL SOLITARY WAVE BREAKING UNDER SUBMARINE RIDGE

LIN Ying-Dian, YU Jun-Yang, LUO Yuan-Ye, YUAN Ye-Ping

(Ocean College, Zhejiang University, Zhoushan 316000, China)

Based on our laboratory flume experiment, the breaking process of internal solitary waves in the presence of submarine ridge and the turbulence generated by wave breaking were studied. In the experiment, the stratified environments of two-layered fluid were set up, and the thickness and density of upper and lower water bodies were quantitatively controlled. The Gaussian terrain with different heights was used to simulate the actual submarine ridge, and the similarities and differences of internal solitary wave breaking process under different heights of submarine ridge were discussed. The experimental results show that the boundary layer separation occurred in the terrain due to the existence of the inverse pressure gradient during the breaking of the internal solitary wave, resulting in the reverse jet and vortex shedding in the bottom boundary layer. The distribution of bottom shear stress during the breaking processes of internal solitary wave breaking was also calculated. In addition, the breaking process of internal solitary waves under the action of submarine ridge was simulated in the experiment, and the influence of ridge on the breaking process and the effect of bottom shear stress were estimated. This study shall enhance our understanding of internal solitary wave breaking under the influence of submarine ridge.

Internal solitary wave; internal wave breaking; boundary layer separation; bottom shear stress

* 国家重点研发计划, 2016YFC1401404号, 2017YFC1405100号; 国际海域资源调查与开发“十三五”课题“西太海山区物理海洋环境及典型海山流场结构”, DY135-E2-2-02号; 舟山市科技计划项目浙江大学海洋学院专项, 2018C81034号。林颖典, 副教授, E-mail: kevinlin@zju.edu.cn

袁野平, 副教授, E-mail: yyping@zju.edu.cn

2020-10-28,

2020-12-29

P731.24

10.11693/hyhz20201000299