基于油气开采的海上油田中长期电力负荷预测

王艳松, 赵 惺, 李 强, 李 雪, 魏 澈

(1.中国石油大学(华东)新能源学院,山东青岛 266580; 2.中海油研究总院,北京 100028)

海上油气田不同于国民经济其他企业、也不同于任何地市,海上油气田的平台设备安装紧凑、生产流程系统化、负荷用电量大、供电可靠性要求高。中长期电力负荷预测结果偏低会造成装机容量不足,影响平台油气生产;预测结果偏高,造成设备投资成本浪费,设备运行效率低[1-2]。因此建立适用于海上油藏开采的中长期电力负荷预测模型具有较高的工程应用价值。中长期负荷传统预测方法[3]包括产业产值单耗法、电力弹性系数法、回归分析法等;现代预测方法包括神经网络预测法[4]、支持向量机预测法、灰色系统预测法等。郭鸿业等[5]将规律性较差的原始序列分解成若干个规律性强的序列,并针对不同的分量采用不同的预测模型。刘俊等[6]在文献[5]的基础上利用计量经济学中的协整检验和格兰杰因果检验分析经济因素与循环分量的关系,进一步提高模型的预测精度。李亦言等[7-8]从人口、经济、地域等方面分析电力负荷的影响因素,分别以模糊聚类法和小波分析法建立多变量负荷预测模型。王雁凌等[9]针对经济新常态下中长期负荷预测样本容量小、建模困难的问题,采用偏最小二乘法建立预测模型。陈毅波等[10]将粗糙集理论与D-S证据理论引入多元回归算法,提高模型的适用性。王宁等[11]将支持向量机方法和多元回归方法通过最优组合预测法,以此提高模型的预测精度。目前各种预测方法都属于确定性数值预测方法,未考虑预测特征的不确定性。海上油气田的油气生产规模、开采工艺、集输工艺随着油藏分布、开采深度和能源战略等因素的影响具有不确定性,笔者将盲数引入回归模型,建立盲数回归预测模型,预测中长期电力负荷的可能值和可信度,解决海上油气田开采不确定性对电力负荷需求的影响。

1 电力负荷特征量提取和筛选

1.1 影响电力负荷需求的特征分析

油气生产规模与电力消耗密切相关,海上油气田的生产主要包括钻采和集输两大关键环节,油田生产的每一个环节都离不开电力。

1.1.1 油气生产规模

海上油气田的提液量、产油量、产气量和产水量等生产规模指标直接决定电潜泵、原油外输泵、电伴热、生产水输送泵和气压缩机等电力设备的使用情况。分析某海上油气田2009—2015年的用电量和表征油气生产规模指标的变化趋势,如图1所示。

由图1可知:2009—2015年期间年用电量稳中有降,年产油量和产气量持续减少,年用电量与年提液量、年产水量变化趋势相近,而与表征产能规模的产气量、产油量的变化趋势相差较大,这体现出了油气田开采的特定阶段内存在着“减产不减电”的负荷需求特性。

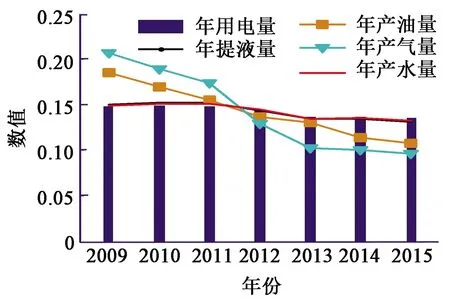
图1 年用电量和表征生产规模指标的变化趋势Fig.1 Change trend of electricity consumption and indicator of production scale

1.1.2 油气开采工艺

在油气藏开发前期,油藏压力高,含水低,实现油井自喷开采,不需要机械采油设备;油气藏开发中后期,油井停止自喷,需要利用高压注水泵向油层注水,在整个油层内建立水压驱动方式,恢复和保持油层压力,再利用电潜泵将原油举升到井口[12-13]。油井的开采工艺直接影响着海上油气田的电力负荷需求,因此将自喷井口数、电潜泵井口数以及注水量作为海上油气田开采环节影响电力负荷需求的特征量。分析某海上油气田2009—2015年的年用电量与表征油气开采工艺指标的变化趋势,如图2所示。

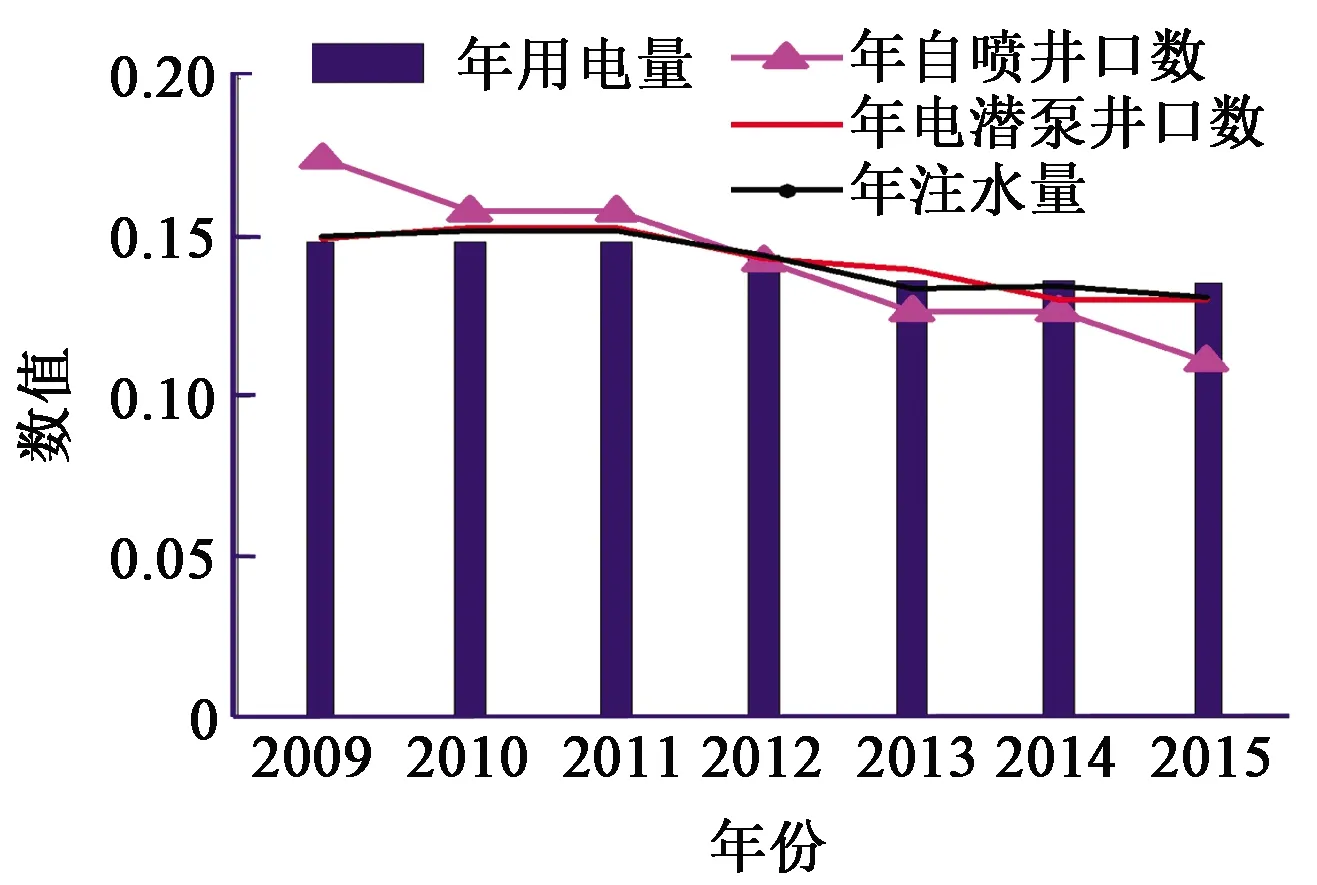
图2 年用电量与开采工艺指标的变化趋势Fig.2 Change trend of electricity consumption and mining process index

从图2可以看出:在2009—2015年期间,自喷井口数持续下降,在2009—2012年期间,电潜泵井口数、注水量和年用电量变化趋势大致相同,稳中有降。在2012—2015年期间,用电量持平,而电潜泵井口数、注水量变化趋势不同。

1.1.3 油气集输工艺

油气集输环节中的脱水、增压、加热和输送工艺的电负荷与原油的流体黏稠度、原油的含水量有关。原油含水率随着油气田不同开采期而变化,通常开采初期,含水量较低,原油黏稠度较大,到了开采中期和后期,原油黏稠度降低,含水量增大,油井黏度随含水率提高而降低。因此在集输工艺方面提取含水率作为影响中长期电力负荷需求的特征量。分析2009—2015年用电量和油气田产油量、含水率变化趋势如图3所示。

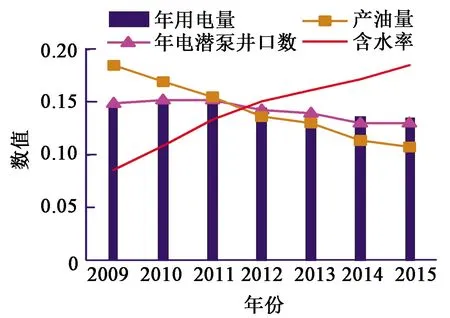
图3 年用电量和油气集输工艺指标变化趋势Fig.3 Change trend of electricity consumption and transportation process index

从图3可知,在2009—2015年期间,年用电量和电潜泵井口数的变化趋势大相同,稳中有降;油气田的含水率在逐年上升,而产油量逐年下降。

1.2 基于逐步回归分析的强特征量筛选

海上油气田的油气生产工艺流程的各环节是一个生产和输送的统一整体,钻采和集输同时进行。从油气生产规模、油气开采工艺和油气集输工艺三个方面提取的年提液量、年产油量、年产气量、年产水量、年自喷井口数和电潜泵井口数、年注水量和原油含水率特征量之间存在高度相关。

逐步回归分析法是一种线性回归模型自变量选择方法[12-14]。逐步回归分析法将特征量一个一个引入回归模型,引入的条件是其偏回归平方和检验是显著的。同时,每引入一个新特征量后,对已入选回归模型的强特征量逐个进行检验,将经检验认为不显著的变量删除,以保证所得强特征量集中每一个强特征量都是显著的。

针对n期历史数据的原始特征量,利用逐步回归分析法进行筛选,筛选后的m个强特征量集可表示为

X=[X(1),…,X(s),…,X(m)]=

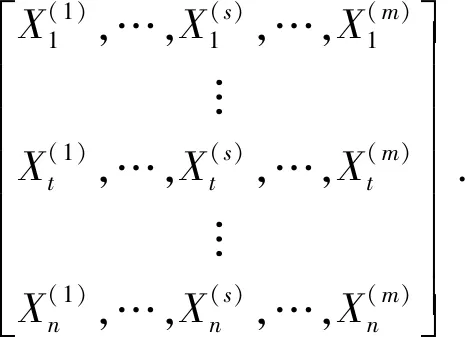
(1)

式中,X(s)为第s个强特征矢量,s=1,2,…,m;t代表年,t=1,2,…,n。

2 盲数的基本理论

盲数[15-17]是处理和解决一系列灰信息及不确定性信息的数学工具,是对灰色数学理论、未确知数学及模糊数学的一种发展。其具体定义如下:

假设G为区间型有理灰数集,xi∈G,αi∈[0,1],其中i=1,2,…,p,那么定义f(x)为G上的灰函数,且

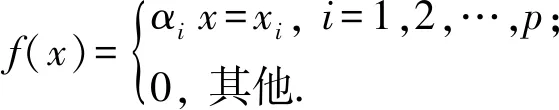
(2)

盲数的运算包含可能值运算和可信度运算两部分,设*表示加、减、乘、除中的任一种运算。

设盲数A和B为

(3)

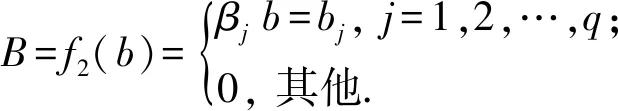
(4)

那么,盲数A与盲数B的可能值运算V(A*B)用可能值矩阵表示为

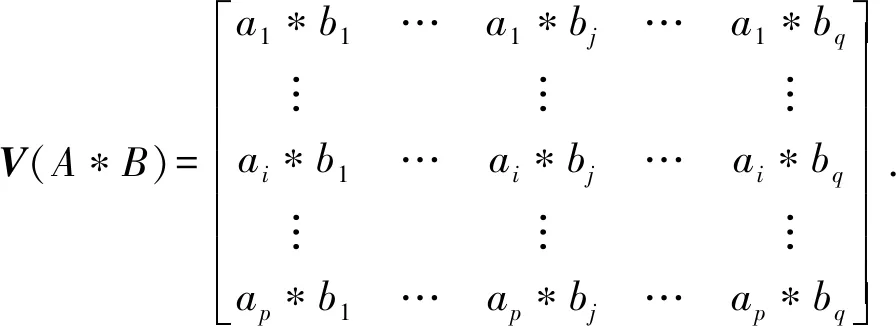
(5)

盲数A与盲数B的可信度运算C(A*B)用可信度值矩阵表示为

(6)

3 盲数模型建立

海上油气田开发规划受油藏可开采储量、开采进度、地质条件和国家能源政策的影响,其生产规模和开采工艺具有不确定性。为了描述海上油田油气开采的不确定性,融入决策者对未来不同开采阶段的研判,应用盲数表示电力负荷预测模型中的强特征量和待预测量。

建立负荷预测盲数模型的关键是强特征量盲数可能值和盲数可信度的确定。

(1)确定各强特征量年变化率盲数的可能值。

(2)确定各强特征量年变化率盲数的可信度。

决策者根据国家能源政策和国际油价行情,考虑油气田不同开采阶段的开采工艺和强特征量发展趋势,研判强特征量X(s)年变化率的p个可能值出现的概率大小,主观决策指导油气生产,建立一个p×p阶的比较矩阵,表示为

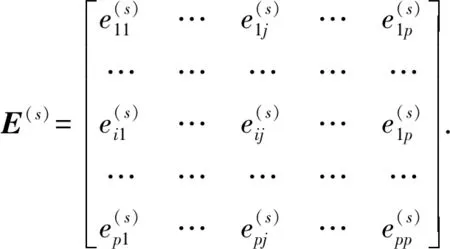
(7)

其中

令

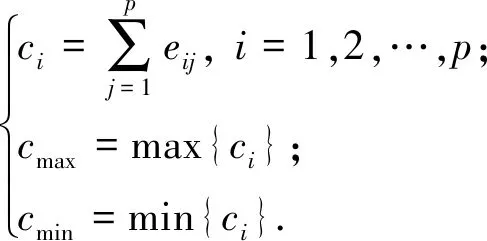
(8)

基于比较矩阵构造判断矩阵G(s),表示为

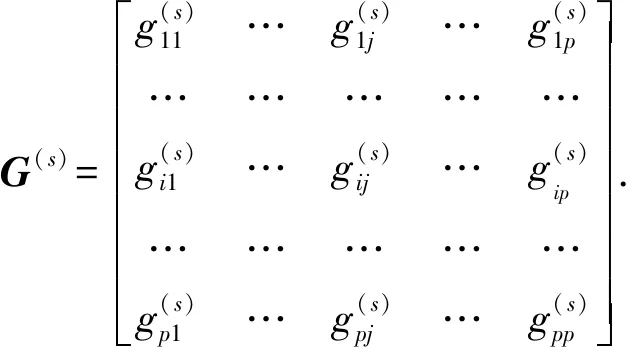
(9)

其中判断矩阵中的元素为

(10)

将判断矩阵G(s)的各元素按列做归一化处理,表示为

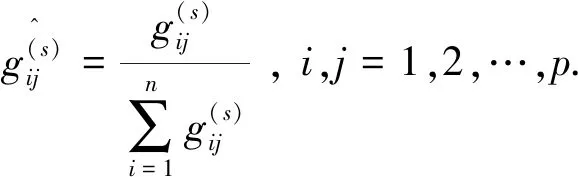
(11)

由归一化的判断矩阵元素可得强特征量X(s)年变化率盲数的可能值的可信度为

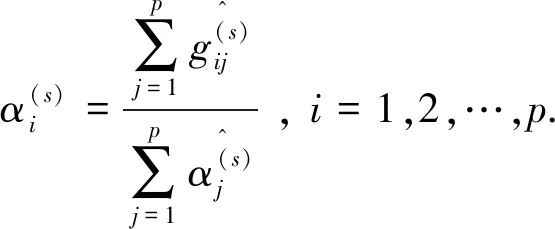
(12)

(3)确定各强特征量年增长率盲数。

(13)

式中,p为盲数阶数;m为强特征量个数。

(4)确定各强特征量盲数。

根据各强特征量年增长率盲数和强特征量的真实值可得各强特征量盲数为

f(X(S))=f(x(S))×u(S),S=1,2,…,m.

(14)

式中,u(S)为待预测年的第S个强特征量真实值。

4 算 例

某海上油气田2009—2019年用电量分别为82 348.3、82 453.8、82 260.7、80 167.0、75 830.8、75 936.0、75 173.8、74 420.5、72 764.8、71 328.2、70 182.3 MW·h。选取2009—2016年用电量为历史数据, 2017—2019年用电量为校验数据,验证所提中长期负荷预测模型。

4.1 特征量变化趋势及相关性

从油气生产规模、油气开采工艺、油气集输工艺3个方面,分析各特征量随时间变化的关系曲线,如图4所示。

由图4可知,2015—2019年海上油田某区块提液量、产油量、产气量和产水量处于减产阶段,部分电潜泵井口关井,产液量、产气量降速加大,含水率平稳上升。另外,年产油量和年产气量的变化趋势相近,年提液量、年产水量与年注水量的变化趋势相近甚至相同,这表明特征量之间存在严重的多重共线性。若将全部特征量引入预测模型中,会使得模型参数方差增大,模型稳定性下降,预测精度降低。

图4 各特征量变化曲线Fig.4 Change curve of each characteristic

4.2 强特征量筛选

应用逐步回归分析法对原始特征量进行筛选,得到的强特征量如表1所示。

表1 逐步回归分析法筛选的强特征量Table 1 Results of stepwise regression analysis

由表1可知,筛选的强特征量为年注水量和年电潜泵井口数,其年用电量与年注水量、电潜泵井口数的关系,如图5所示。

图5 年用电量与电潜泵井口数、年注水量关系Fig.5 Relationship between annual power consumption and annual water injection, number of electric submersible pump wellhead

由图5可知,被筛选出的强特征量年注水量、年电潜泵井口数和待预测电量之间呈明显的线性关系。

4.3 负荷预测结果

利用强特征量与预测电量之间的线性关系,建立多元线性回归模型,对2017—2019年用电量进行预测,并与未筛选特征量的回归模型、时序外推模型和提液量单耗法的预测结果进行对比,如表2所示。

表2 不同模型的负荷预测结果及其精度对比Table 2 Load forecasting results of different models and accuracy comparison 104 kW·h

由表2可知,基于强特征量的回归模型预测精度最高,最大预测误差为-2.17%,平均误差为-1.81%;由原始特征量建立的回归模型,最大预测误差达-6.14%,时序外推预测模型通过拟合历史电力负荷序列来实现预测,预测精度最低,最大误差为-9.94%;提液量单耗预测模型最大误差为-3.77%,预测精度也不高。

为了进一步考虑油气田开采的不确定性,将各强特征量盲数化,建立盲数回归预测模型:

Y=λ0+λ1f(X(1))+…+λlf(X(s))+…+λsf(X(m)).

(15)

式中,Y为预测量;f(X(S))为强特征量盲数;λ0,λ1,…,λl,…,λs为回归模型系数;m为特征量个数。

应用盲数回归预测模型,进一步给出预测结果的可能值和可信度,如表3所示。

由表3可知,负荷真实值均落在盲数回归预测模型给出的负荷预测区间,随着盲数模型阶数增大,各预测区间变窄、可信度降低,各预测可能值区间均属于真实值的[-5%,+5%]偏移区间。选取3阶盲数预测模型,对海上油田未来2020—2029年的年用电量进行预测,预测结果如表4所示。

表3 盲数回归模型负荷区间预测结果Table 3 Load forecast results of blind number regression model

表4 海上油田2020—2029年用电量预测结果Table 4 Forecast results of electricity consumption of offshore oilfield in 2020-2029

5 结 论

(1)应用逐步回归分析法筛选的强特征量进行负荷预测的误差小于3%,比原始特征量的负荷预测精度高。

(2)对于油气田开采规划,决策人研判强特征量发展趋势和区间概率,应用盲数解决了油气开采的不确定性。

(3)盲数回归预测模型给出了电力负荷需求可能值区间及其相应的可信度,其预测区间小于预测值的±5%偏移区间,降低了电力负荷预测风险。