应用人工神经网络分析织物的形态与性能之间的关系

余志才,钟跃崎,2

(1.东华大学 纺织学院 上海 201620; 2.东华大学 纺织面料技术教育部重点实验室 上海 201620)

随着计算机硬件的不断发展,数据科学获得了纺织学界的广泛关注,许多优秀的学习算法被提出并应用到实际纺织生产中[1-3]。 同时,得益于三维扫描技术持续更新,越来越多的科研工作者着眼于织物三维悬垂模型的重建[4-6]。 但是,利用神经网络探究织物三维悬垂形态和织物力学性能的关系还鲜有涉及。 鉴于此,本文就织物三维悬垂形态及其力学性能之间的相互映射关系展开研究。

首先,探究通过织物经向纬向的弯曲刚度和剪切刚度以及织物的面密度,预测织物悬垂特征,如悬垂系数、悬垂角的可行性[7],该研究属于织物力学性能对织物悬垂形态的预测。 其次,通过悬垂形态特征和织物面密度预测其力学性能,即形态对力学性能的预测。 特别地,从形态预测织物力学性能的研究,有助于给用户提供一种无需精密测试的仪器,可简化了解织物基本力学性能的途径,可用于网络空间或者远程交互场景。 需要说明的是,本文仅研究织物的弯曲刚度及剪切刚度与织物三维悬垂形态之间的关系,因Morooka 等[8-9]证明了织物的面密度、弯曲刚度和剪切刚度与织物的三维悬垂模型之间的关联性最高,故选择弯曲刚度和剪切刚度作为突破口更具代表性。

1 数据的采集

将51 种织物样本在相同的条件下洗涤并熨烫以除去织物表面的褶皱。 在恒温恒湿实验室利用KES-FB1 织物风格测试仪(日本加藤技研株式会社)测试织物的经向剪切刚度Swarp和纬向剪切刚度Sweft;用KES-FB2 织物风格测试仪(日本加藤技研株式会社)测试织物的经向弯曲刚度Bwarp和纬向弯曲刚度Bweft;用MS105DU 精密天平(瑞士Mettler-Toledo)测试织物样本的面密度Gk。

在远离布边的位置,从每种织物上裁剪出半径为120 mm 的圆形样本,并标记中心点位置。 将织物在恒温恒湿实验室,温度为(20±2) ℃,相对湿度为(65±4)%,调湿24 h。 利用文献[10]中给出的扫描装置对51 种织物的悬垂形态进行扫描,并将扫描的三维点云封装为三角形网格。 通过文献[9]提出的网格重采样方法对三角形网格进行重采样,使其具有相同的顶点数目和三角形拓扑结构,在具体实现时,本文中所使用的每个重采样之后的三维悬垂模型具有5 172 个顶点,然后对每个三维悬垂模型计算由多组悬垂指标的主成分所构成的形态特征ICpca,具体步骤如下。

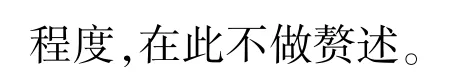
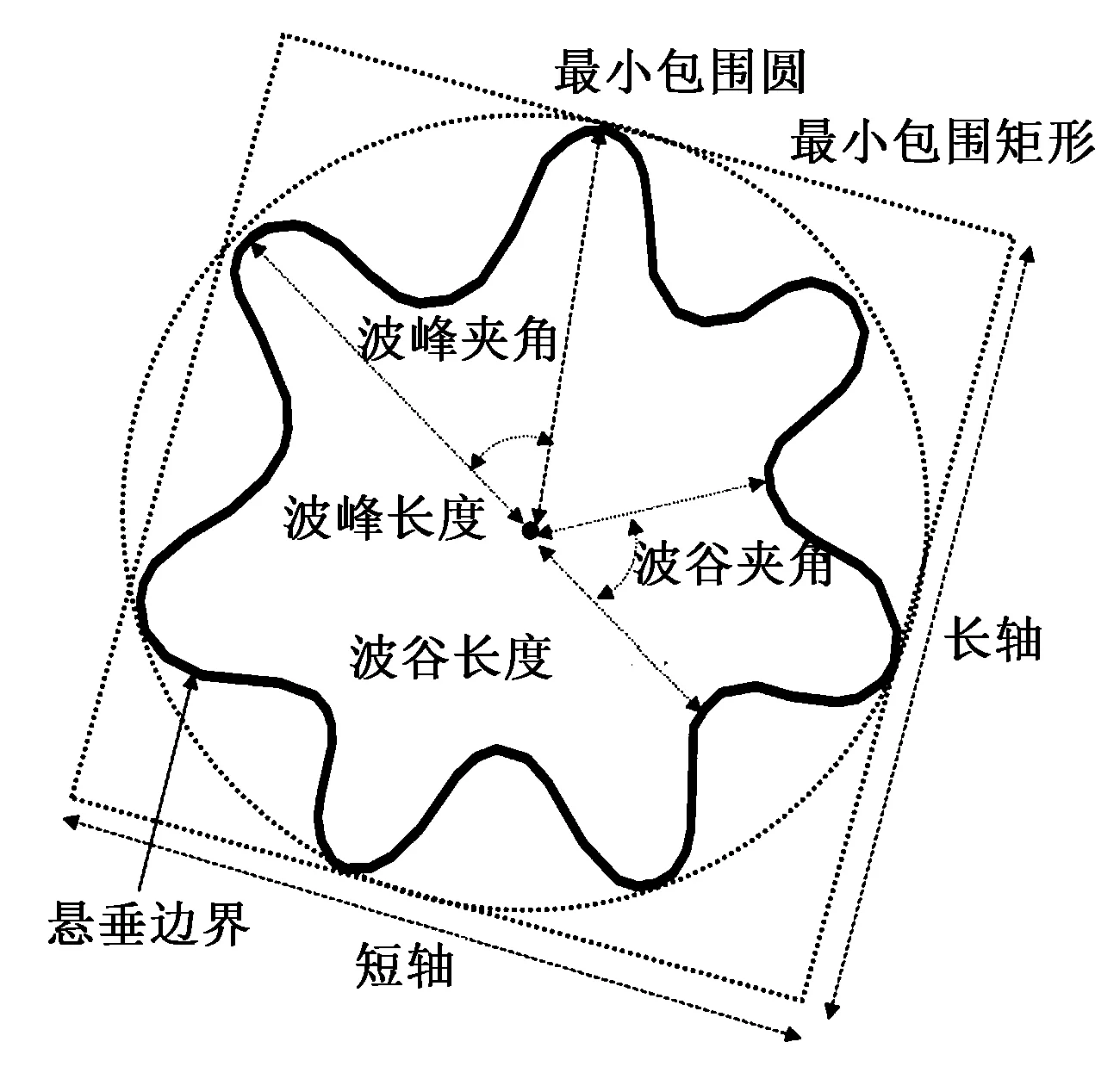
图1 织物悬垂模型及悬垂指标的定义

步骤2:将所有悬垂模型的悬垂指标串联组成悬垂指标矩阵MS_Indicator, 矩阵中每行代表1 个三维悬垂样本,每个样本包含以上9 个悬垂指标作为其特征描述。

步骤3:将MS_Indicator中每列向量进行归一化处理,去除各列的量纲。 然后用主成分分析法(Principal Components Analysis, PCA)计算MS_Indicator的主成分与其对应的累积贡献率。 悬垂指标的主成分与累积贡献率如图2 所示。 由图可见, MS_Indicator的前5 个主成分的累积贡献率已经超过95%,因此,可将悬垂指标的前5 种主成分组成的特征向量作为MS_Indicator的主成分特征矩阵MS_pca_Indicator, 用该矩阵的每行代表1 个三维悬垂样本,记为Ipca∈R1×5。

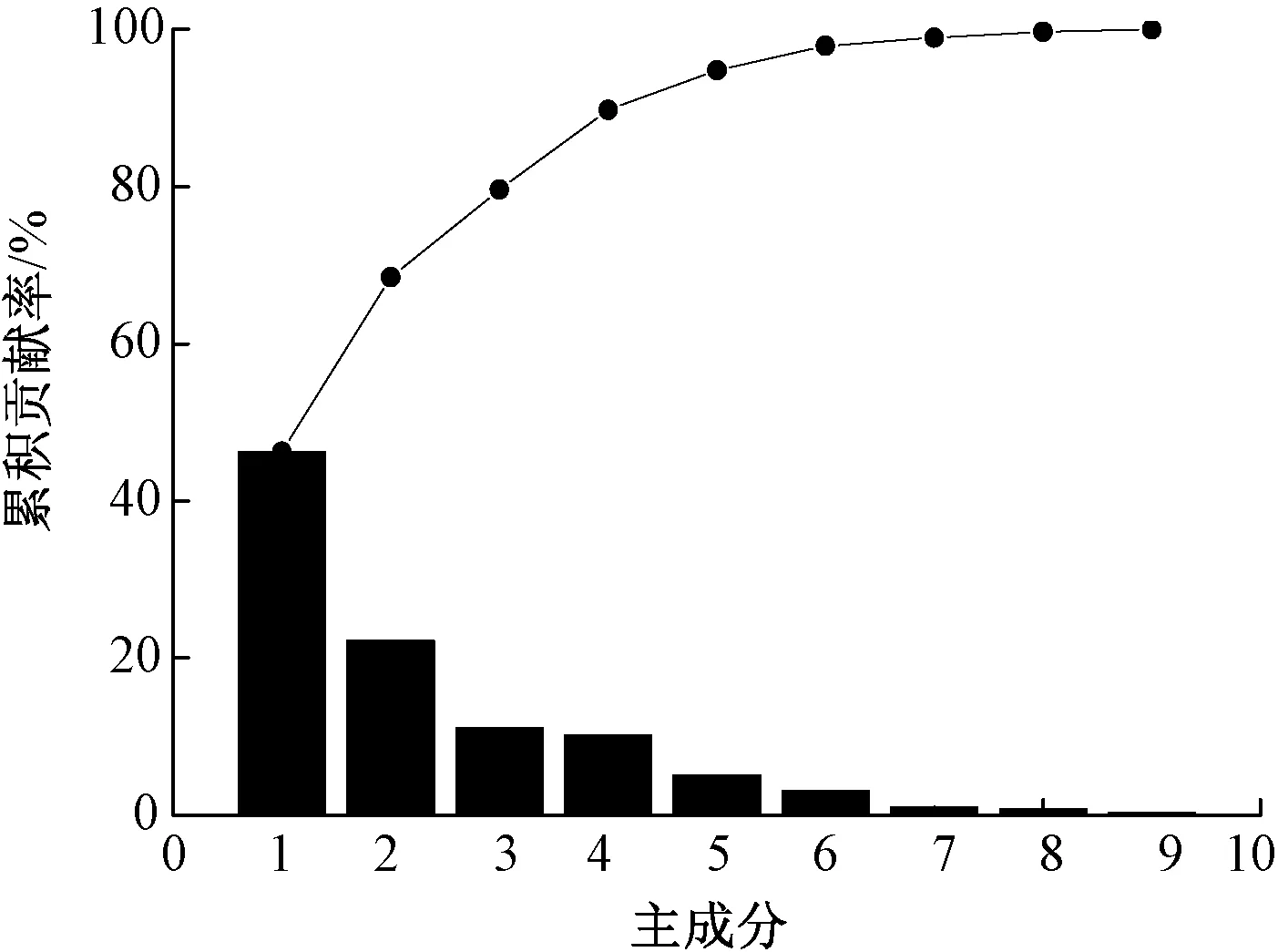
图2 悬垂指标的主成分与累积贡献率

步骤4:计算重采样悬垂模型顶点处的最大曲率值。 由于每个重采样模型具有5 172 个顶点,因此每个模型对应5 172 个最大曲率值。

显然,若直接用5 172 个曲率值构造特征向量会造成维度过高的现象,不利于计算和对比分析。因此同样采用PCA 降维处理的思路,求得每个重采样模型的曲率主成分特征Cpca∈R1×5, 然后按照ICpca=0.855×Ipca⊕0.145×Cpca求得每个重采样模型的形态特征ICpca,其中⊕代表串联,使得ICpca∈R1×10。

2 基于力学指标和面密度预测悬垂模型形态特征

本文实验包含以下几个步骤:

步骤1:将51 种织物对应的Gk、Bwarp、Bweft、Swarp、Sweft串联组成1 个5 维特征向量Fg_m∈R1×5;

步骤2:计算51 种织物的对应悬垂模型悬垂系数(DC)和悬垂角(DA);

步骤3:搭建并训练1 个BP 神经网络,如图3所示,其中输入层包含5 个节点,分别对应输入特征Fg_m的5 个元素;输出层包含1 个节点,即DC 或DA中的1 个。 换言之,利用相同结构的BP 神经网络训练了2 组权重系数,分别实现对DC 和DA 的拟合。 此外,该BP 神经网络的损失函数选用均方误差(Mean Squared Error,MSE),并采用Sigmoid 函数作为非线性激活函数。

经过多次实验,发现当隐含层包含3 个节点时预测效果最佳,因此将隐含层的节点数目设置为3。

图3 基于Fg_m预测DC 或DA 的BP 神经网络结构

为了避免数据分布不匀带来的误差,预测过程采用了 K 折交叉验证方法(K - Fold Cross Validation)。 即将全部样本(51 种织物)分成k = 10个不相交的子集{ds1,ds2,…,dsi,…,dsk}, 每次取出1 个子集作为测试集,其余k - 1 个子集作为训练集。 10 折交叉验证后每个样本均被当作测试样本测试1 次,即51 种织物均对应1 个预测值。 最后计算样本的预测值相对误差绝对平均值以及预测值与真实值的相关系数。

使用上述BP 神经网络对悬垂系数和悬垂角预测的结果如图4 所示。

由图4(a)可见,DC 预测值与真实值的相关系数为0.943 3,DC 预测值的相对误差绝对平均值为8.15%。 图4(b)中DA 预测值与真实值的相关系数为0.940 6;DA 预测值的相对误差为5.1%。 该结果说明通过BP 神经网络,从织物的力学性能及面密度(即Fg_m)预测织物悬垂特征(DC 或DA)是可行的,但预测精度还有待进一步提升。

图4 悬垂系数和悬垂角预测结果

3 基于悬垂模型形态特征预测织物力学性能

将织物的面密度作为已知条件,结合织物的悬垂形态去预测织物的弯曲刚度和剪切刚度,主要出于两方面考虑。 一是织物的面密度易于测量,且织物面密度与织物的其他结构参数和力学性能都存在很强的相关性[15];二是Pan 等[16]的研究结果证明,将织物的面密度引入到织物悬垂结果的分类中,会使得悬垂模型的分类更有意义。

因此,将ICpca与Gk结合,尝试对织物的Bwarp、Bweft、Swarp、Sweft进行预测,具体步骤如下:

步骤1:将织物的面密度( Gk)与ICpca串联组成1 个新的特征向量Fg_IC∈R1×11;

步骤2:创建以Fg_IC为输入参数的BP 神经网络,具体结构如图5 所示。

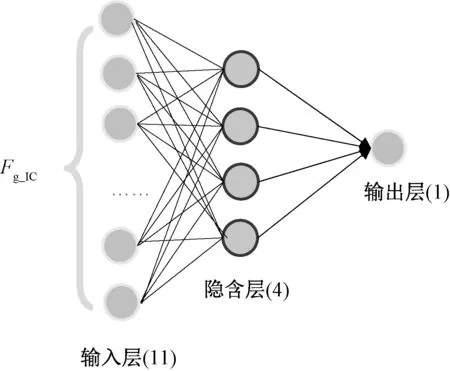
图5 基于Fg_IC 的BP 神经网络结构

该BP 神经网络的输入层包含11 个节点,输出层仅包含1 个节点,用于预测织物力学指标Bwarp、Bweft、Swarp、Sweft中的1 个。 该网络的损失函数为均方误差,采用Sigmoid 函数作为非线性激活函数。为了避免数据分布不匀带来的误差,同样采用10 折交叉验证法进行预测。

需要说明的是,对应这4 种不同的力学预测值,需分别构造4 个相同架构的BP 神经网络。 训练完成之后,可得4 组不同的神经网络权重矩阵。 通过大量实验,发现当神经网络的隐含层包含4 个神经元时预测效果最佳。

使用上述神经网络对经纬向弯曲刚度和剪切刚度预测结果如图6 所示。 图6 示出,织物经、纬向弯曲刚度预测值的相对误差绝对平均值要高于经、纬向剪切刚度预测值的相对误差绝对平均值,而经、纬向弯曲刚度预测值与真实值的相关系数略高于经、纬向剪切刚度预测值与真实值的相关系数。

很显然,使用BP 神经网络从织物形态特征预测其力学性能指标的准确率并不高。 但是,这种探索同时也说明了使用人工神经网络进行形态到力学性能的预测并非全无可能,未来还有更多的工作可以在该方向展开。 比如下面的分类实验,将回归问题降低难度,当作1 个分类任务进行探究。

4 织物柔软程度的分类

织物悬垂形态与织物弯曲刚度或剪切刚度之间的预测问题也可当作织物柔软等级的判定问题。 若将织物的经向、纬向弯曲刚度之和与Gk的比值记为rb/g,则根据织物的悬垂形态预测织物rb/g的等级,相当于根据织物的悬垂形态预测织物的柔软等级。

4.1 织物rb/g的分类

本文实验包含以下步骤:

步骤1:利用K 均值聚类方法(K-Means)将51 种织物按照rb/g分为3 个类别,分类结果如图7所示。

其中类别1 包含24 种织物,该类织物的rb/g值较小;类别2 包含20 种织物,该类织物的rb/g相对于类别1 的织物较大,类别3 包含7 种织物,其对应的rb/g最大。 需要说明的是,当织物的种类和样本数量无穷大时,rb/g将会是一条连续曲线。 此时对其聚类,相当于人类主观地分解一个连续数据空间,类似于指定人群的高矮胖瘦一样。 这里所给出的3 个类别,可以看作是上述真实数据分布的一种简化。

图6 经纬向弯曲刚度和剪切刚度预测结果

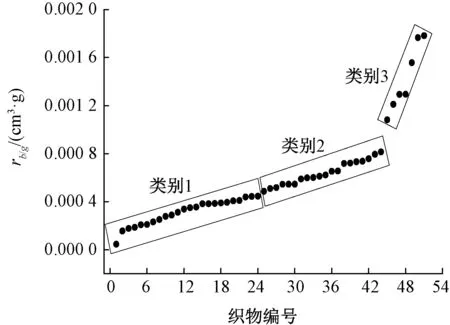
图7 织物rb/g 的3 个类别

步骤2:利用文献[10]采用的三维扫描装置,在相同的实验条件下,将每种织物对应的圆形试样分别重复扫描50 次,51 种织物共采集2 550个悬垂模型。 根据图8 所示的方法改变相机位置采集不同的悬垂模型图像,具体做法为首先建立如图8(a)所示的坐标系,在虚拟环境中确定7 个相机位置,其中位置1 在Z 轴上,相机2 ～7 均匀分布在与OZ 轴垂直的平面上,然后在虚拟环境中将悬垂模型渲染为图8(b)所示的灰度图像,渲染的参数为:三角形的边设置为无色、三角形表面颜色设置为白色、三角形表面的漫反射系数设置为0.5、表面的环境光系数设置为0.3、表面的透明度设置为0.95。

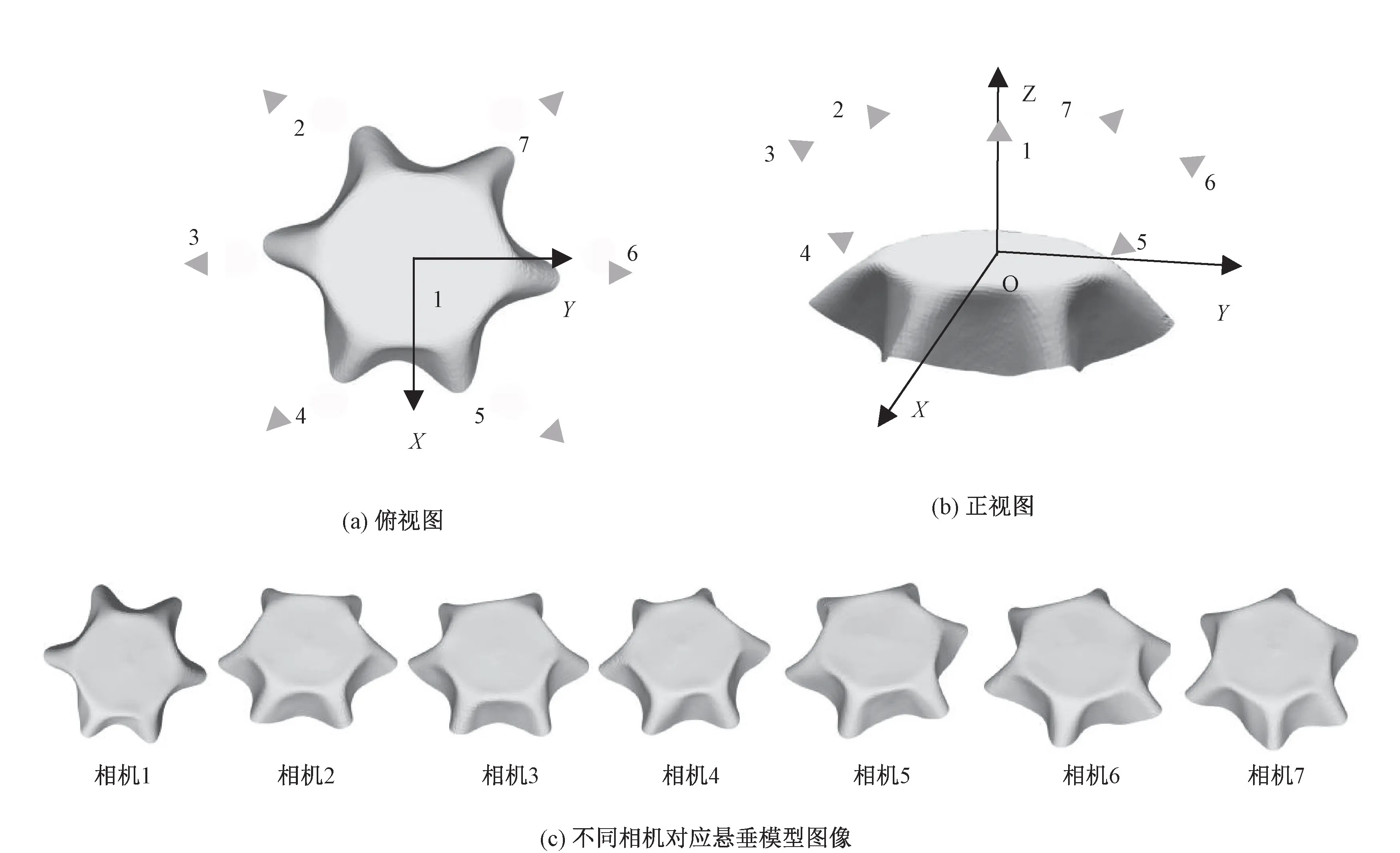
图8 改变相机位置采集不同的悬垂模型图像

由图8 可见,通过改变相机位置可以提高图像的多样性,每种织物均对应350(50×7)张灰度图像,最终51 种织物共采集13 850(51×350)张图像,每张图像均用其rb/g类别作为分类任务的真值标签。 即给定任意一张图像,如果该图像属于图7 中类别Ci中的任意一种织物,则将该图像的标签设置为i。

步骤3:将渲染的灰度图像经过翻转、平移、旋转、改变图像明亮度和裁剪缩放等操作[17]进行数据增广(Data Augmentation),最终统一为224×224 的RGB 图像。 然后按照8 ∶1 ∶1的比例将13 850 张图像分成14 280 张图像组成的训练集、1 785 张图像组成的验证集和1 785 张图像组成的测试集。 进行数据增广的目的是便于深度神经网络拥有足够的数据进行训练,同时保持良好的泛化性能。

步骤4:分别使用在ImageNet 图像数据集上经过 预 训 练 的ResNet18、 ResNet34、 ResNet50[18]和EfficientNet-B0、EfficientNet-B1[19]进行迁移学习,实现对织物的rb/g分类。 本文研究采用ResNet 分类模型的原因在于其易于训练,可以作为基准网络来对比其他分类模型的效果;而EfficientNet 是目前公认的参数量相对较小且分类效果较好的分类模型,由于实验室硬件限制,本文研究仅使用EfficientNet系列中参数量较小的2 种模型,即EfficientNet-B0、EfficientNet-B1。

由于本文所用数据量相对于ImageNet 等大型数据集来说较小,容易发生过拟合,因此在训练过程中还需使用L2 正则化(L2 regularization);其中5 种分类模型的权重衰减系数均设置为0.001。 分类模型的运行平台为便携式计算机,其配置有主频为2.8 GHz 的Core i7700 HQ 英特尔处理器和显存为6 GB的NVIDIA GTX 1060 显卡。 对于所有的分类模型,统一设置损失函数为交叉熵损失,优化器的类型为随机梯度下降法,学习率为0.000 5,训练周期为16。

4.2 基于悬垂模型的织物rb/g分类结果

分类模型的验证集和测试集准确率如表1所示。

由表1 可见ResNet18 在测试集上的分类准确率要优于ResNet34 和ResNet50。 EfficientNet-B0 的分类准确率要优于EfficientNet-B1。 RenNet18 和EfficientNet-B0 的模型相对简单,因此过拟合的程度相对于其他网络模型较小,其分类准确率要优于其他网络模型。 且EfficientNet-B0 的分类准确率优于ResNet18,这与其网络架构更宽更深有关,当分类任务更复杂时,这样的网络通常表现更佳。

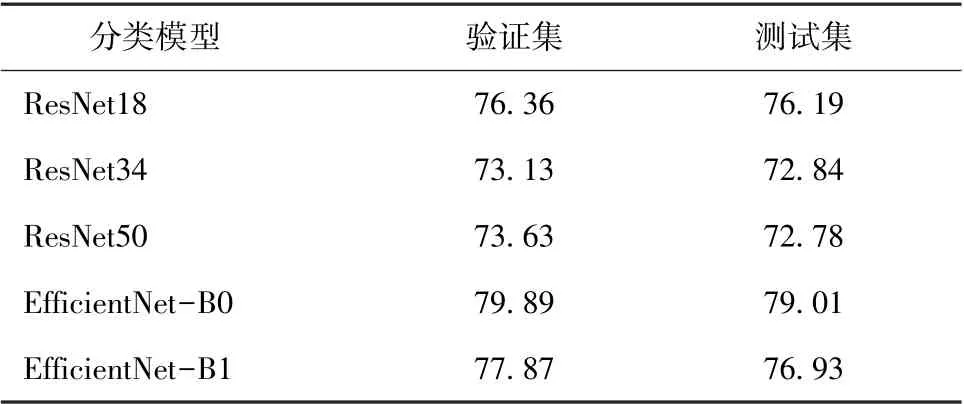
表1 分类模型的验证集和测试集准确率 %

由表1 可见,本文采用的5 种分类模型在对织物rb/g分类时,测试集的准确率均低于90%。 原因在于此前指定的类别真值实为连续曲线的人为分段,即这里的分类任务仍然面临悬垂模型的模糊边界问题。 虽然图7 中织物具有不同的rb/g, 但是这不能证明类别1 和类别2 对应的悬垂模型具有清晰的分类界限,即图7 中类别1 和类别2 仍然存在悬垂结果交叉的可能性,这与我们熟知的不同织物悬垂形态有可能高度相似这一现象是吻合的。

为了衡量上述5 种分类模型的分类准确率与人眼所能达到的分类准确率之间的关系,测试了织物rb/g3 个类别的人类大脑识别率,具体步骤如下。

步骤1:将上述51 种织物分成3 个类别,分类结果与图7 相同;每种织物挑选5 组悬垂模型灰度图像,51 种织物共计255 组图像;

步骤2:对10 名具有纺织专业背景的技术人员进行培训,告知步骤1 中所示的255 组图像中每张图像所属的类别,嘱其认真辨别每个类别的图像特征;

步骤3:让经过培训的技术人员测试153(51×3)组并未见过的悬垂图像,即根据图像判断织物rb/g的类别,计算织物rb/g3 个类别的人类大脑识别率;

织物rb/g3 个类别的人类大脑识别率如表2 所示。 由表2 可见,织物rb/g3 个类别的人类大脑识别率均值为81.66%,该结果表明人眼在对织物悬垂形态进行分类时,同样存在认知上的不确定性,该结果验证了通过深度神经网络进行织物柔软度分类识别的困难所在。 事实上,采用深度神经网络(如EfficientNet-B0)在3 个类别任务上所达到的验证集与测试集最高准确率,即表1 中的79.89% 与79.01%与人类大脑识别率81.66%相比,相当于人类大脑识别率的96.8%～97.8%。 综合来看,织物柔软程度的分类问题通过深度学习的方法解决,同样具有一定的可行性。

表2 织物rb/g 3 个类别的人类大脑识别率 %

5 结 论

本文旨在寻找通过人工神经网络建立织物悬垂形态与织物力学性能之间相互映射的可能途径。 通过大量实验验证与分析,得出以下结论:

①为了能够在织物的力学性能和悬垂形态之间建立一种互相映射关系,并探索出一种根据悬垂模型或织物面密度预测织物力学性能的可能途径,探究了织物的力学性能到形态的映射。 设计了1 个BP 神经网络,利用K 折交叉验证的方法,验证了根据织物的面密度、经向弯曲刚度、纬向弯曲刚度、经向剪切刚度、纬向剪切刚度等5 种参数的组合特征Fg_m预测织物的悬垂系数和悬垂角是可行的。

②探究了织物的形态到力学性能的映射。 设计了1 个BP 神经网络,利用K 折交叉验证的方法,验证了根据织物的悬垂特征与面密度的组合特征Fg_IC预测织物的经向纬向弯曲刚度和经向纬向剪切刚度也是一种可行的办法。 结果显示基于Fg_m的悬垂系数和悬垂角预测结果要优于基于Fg_IC的经向纬向弯曲刚度和经向纬向剪切刚度预测结果。

③将悬垂形态与力学性能间的关系看作1 个分类任务时,采用多种深度神经网络进行悬垂图像的分类识别,与人类大脑在面临同样任务时的准确率水平较为类似,三分类任务相当于人类大脑识别率的97.8%,说明在织物形态到力学性能的推理过程中,特别是从最少量输入条件下的“形态”推理预测“性能”时,深度学习方案是一个可行的选择。