基于复合控制两级逆变器系统优化

吴玉良，王 凯，王成悦，赵艺雷，徐文斌

（合肥同智机电控制技术有限公司，安徽 合肥 236000）

0 引 言

随着社会科技的进步，逆变器的应用越来越广。因此对于整体性能有着更高的需求，要求系统输出电压具有良好的稳定性、响应的快速性以及优良的精确性。为了符合系统的性能要求，则需将多种控制算法结合形成复合控制应用于整个系统。

逆变器系统应用主要由单级和两级串联结构组成，其中单级逆变器结构简单，元器件使用较少，但是单级系统一般没有电气隔离，存在一定的安全隐患。两级串联结构有很多种，本文采用的是前级推挽结构串联后级全桥逆变电路。该结构具有输入范围较宽，同时输入输出具有电气隔离，以及前后级可以进行功率解耦，分别控制等优点[1]。

本文主要包括4个部分：首先，阐述了两级逆变器系统的工作原理；其次，设计了双环控制策略和重复控制器，并且搭建整个逆变器系统Simulink仿真模型；然后，系统在不同控制策略下仿真分析对比；最后，将复合控制算法应用在基于TMS320F28069芯片的2 kW逆变器系统中，进一步验证其控制算法的正确性。

1 二级逆变器系统原理

二级逆变器系统是由前级推挽结构串联后级逆变电路组合而成的，其中系统框图如图1所示。本文中的直流输入电压是20～30 V可变的，然后经过推挽变压器升压，再进行二极管整流后给母线电容充电。得到稳定母线电压传输给逆变器作为输入源，经过全桥逆变后再进行LC滤波进而得到220 V/50 Hz正弦交流输出。

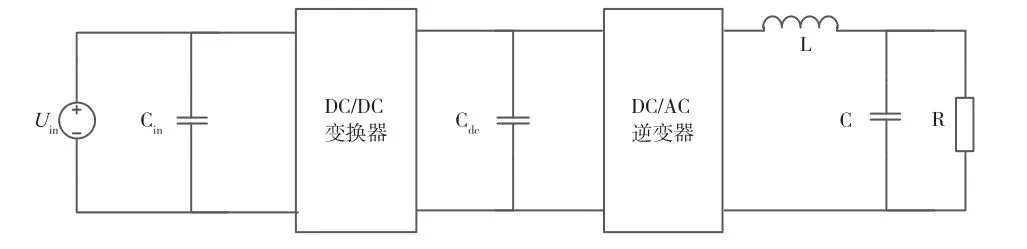
图1 逆变器系统框图

其中逆变器采用单极性正弦脉冲调制（Sinusoidal Pulse Width Modulation，SPWM）的发波方式，由4个MOS管组成低频桥臂和高频桥臂。低频桥臂是以50 Hz的频率两个MOS管交替导通，而高频桥臂是MOS管开关频率上下两管交替导通，且导通的占空比随着正弦信号变化。为了防止两组上下桥臂直通，则每组相互导通的MOS管必须留有一定的死区时间。单极性SPWM控制方式由于存在低频桥臂，这样就会减小MOS管开通和关断损耗。

2 复合控制策略设计

2.1 双环控制策略设计

本文采用电压外环和电流内环组成的双环控制系统，其中外环控制输出电压的幅值，内环基准给定是外环输出，这样内环可以起到输出限流的目的，同时加快系统响应速度[2]。整个系统控制设计流程图如图2所示。

由图2可知，外环给定参考电压与输出反馈电压进行比较作差，经过电压环PI调节器后输出即作为电流内环的给定值，同时为了防止输出电流出现扰动信号，所以将负载电流作为前馈补偿到电压环中，这样改善了系统抗负载扰动能力。电流环得到给定值后与反馈的电感电流进行比较作差，再经过PI调节器后输出值与三角载波进行比较得到相应的驱动信号，其中在电流环中也将输出电压作为前馈环节补偿到电流环PI输出中，同样提高了电流环的抗干扰能力[3]。

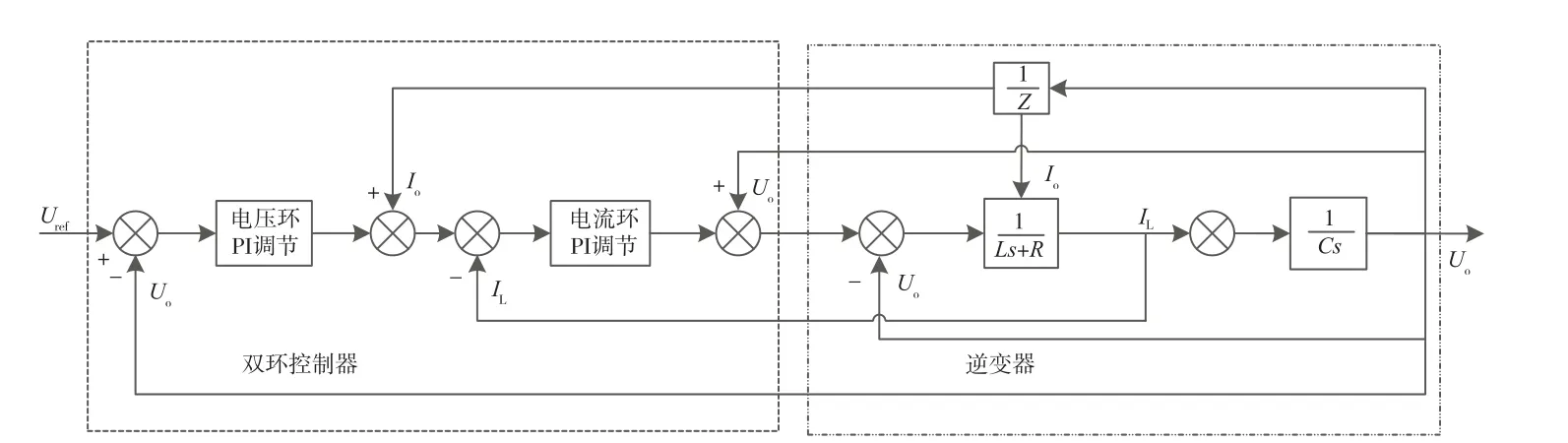
图2 双环控制流程图

根据上述逆变器的原理图，可得到系统的状态方程如式（1）[4]所示：

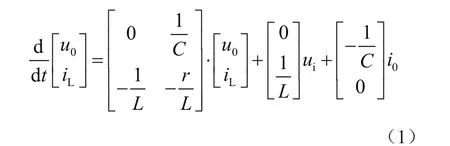
式中，r为电感的内阻，通过整理可得当系统空载时（R→∞）的传递函数如式（2）：

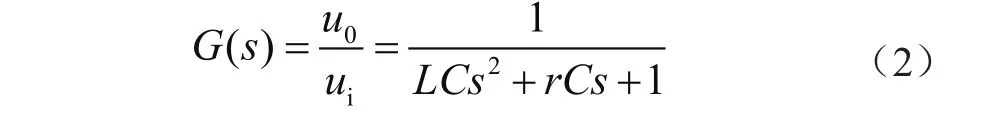
当系统加入电压环和电流环进行控制时，由图1整个系统框图可得出系统在输入是正弦参考电压信号时闭环传递函数分别如式（3）所示：

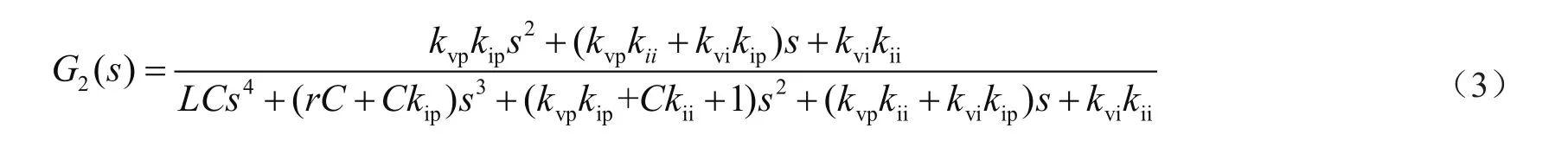
式中，kvp,kvi,kip,kip分别表示电压环的比例和积分系数以及电流环的比例和积分系数；L,C,r分别表示逆变器滤波电感电容还有电感的内阻。将具体参数设计代入式（3）中，可得如下传递函数：

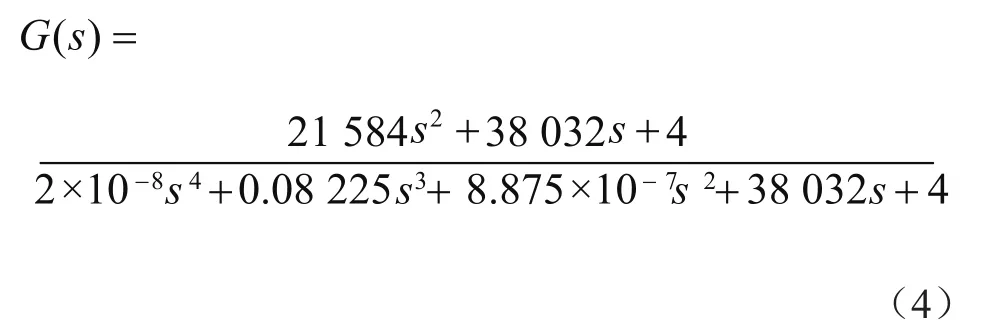
2.2 重复控制

重复控制是一种基于内模原理的控制方式，主要针对一些周期性的扰动进行抑制，从而实现系统高精度的稳态输出。由于重复控制是检测到系统在一个周期的某个时刻出现扰动信号，则认定在下个周期的相同时刻也会出现同样的扰动信号，进而对下个周期该时刻的信号进行校正补偿[5]。在逆变电源中特别是带非线性负载（RCD负载）时，输出波形的谐波分量较大且质量较差，采用重复控制其输出波形将得到改善。由于重复控制是在下一个周期再对系统的扰动信号进行校正，因此系统将会延时一个周期，这也将导致系统的动态响应变差[6]。本文将重复控制和双环控制结合运用，使得系统在稳定的情况下，既能够快速响应又能够高精度稳态输出。重复控制的系统框图如图3所示。

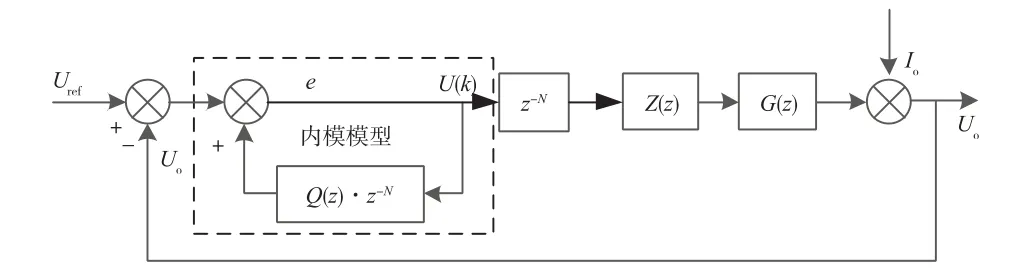
图3 重复控制系统框图

图3中N表示一个周期的采样次数，Q(z)为低通滤波器，C(z)为重复控制的补偿器。根据图3可得到内模模型的传递函数和差分方程分别如式（5）所示：

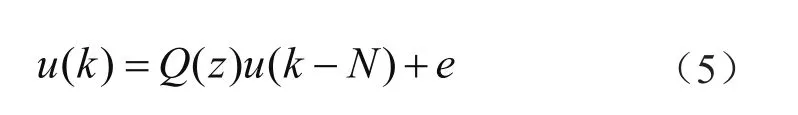
通过仿真分析取Q(z)=0.95，这样由式（5）可得重复控制将上一个周期输入信号衰减5%叠加到当前周期的误差信号中，这样减小了系统的扰动误差累积过程直到系统稳定输出。图3中C(z)补偿器是重复控制的核心，针对误差信号进行相位和幅值补偿校正，从而快速抑制外部扰动信号，使系统达到稳定输出。为了简化数字控制设计，其中C(z)包括重复控制增益k，相位超前环节zk两部分，如式（6）所示：

逆变器系统中的载波频率是19.2 kHz，采样周期也是19.2 kHz，正弦波频率50 Hz，得到N=384，其中k设计为0.125，仿真分析得出相位补偿zk=z8。

2.3 系统仿真模型

根据上述图1系统的原理框图，可搭建系统的Simulink仿真模型如图4所示，其中逆变器控制部分采用S-Function编写。

图4 二级逆变器系统Simulink仿真模型

3 仿真与实验结果分析

3.1 仿真结果分析

根据图4搭建的Simulink系统模型，利用双环控制策略进行不同状态下的仿真得到波形如图5所示，并且通过快速傅里叶变换（Fast Fourier Transform，FFT）对额定负载和整流性负载输出电压波形进行分析得到总谐波失真（Totel Harmonic Distortion，THD）分别为2.1%和3.6%。

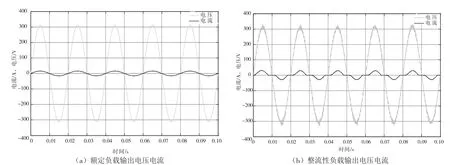
图5 不同状态系统输出波形

根据上述系统模型，对其采用双环控制和重复控制组合成的复合控制进行仿真分析，得到图6，并通过FFT进行两种工况对输出电压波形分析得到THD分别为1.07%和2.27%。

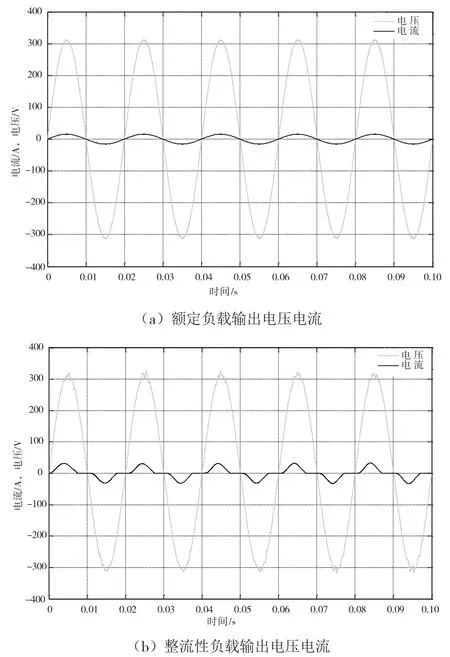
图6 不同状态系统输出波形

通过对比分析上述波形图可得到，复合控制比双环控制在额定负载稳态输出的情况下电压输出的THD更小，动态性能更好。特别是在整流性负载时，复合控制输出电压的THD减小很多。

3.2 实验结果与分析

本文基于TMS320F28069芯片搭建2 kW逆变器实验平台进行验证仿真结果，输入是20～30 V直流电，经过推挽升压到母线电压，最后通过逆变器控制输出220 V/50 Hz的正弦交流电。其中逆变器采用复合控制策略，实验得到驱动波形以及不同状态电压波形如图7所示。通过对比实验结果分析可知，复合控制策略与仿真的结果基本一致。

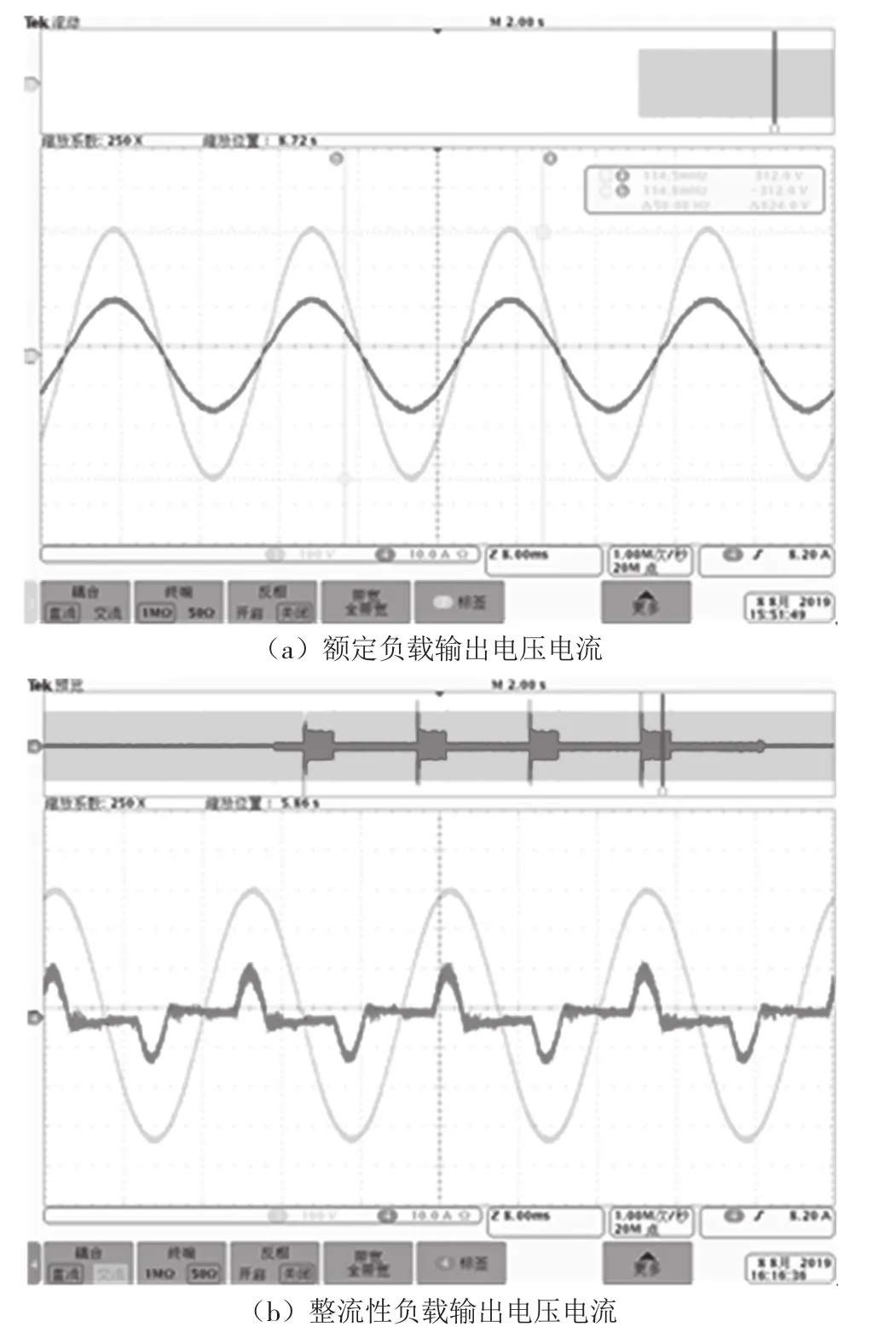
图7 实验驱动和不同状态输出电压电流波形

4 结 论

通过仿真分析可得，复合控制在额定负载和整流性负载情况下，系统输出的电压波形THD相比双环控制分别减少了约1%和1.3%。同时在动态投卸载的过程中，复合控制也能快速响应外部扰动。并且实验结果与仿真结果也是基本保持一致的。综上所述，由双环控制和重复控制形成的复合控制策略使得系统整体的性能得到了一定的改善，输出波形的质量得到了提高。