侧风影响下简化配对进近安全区域研究∗
2021-05-25
(中国民用航空飞行学院空中交通管理学院 广汉 618300)
1 引言
随着航空运输在整个交通运输业所占比重的持续增加,各枢纽机场容量日趋饱和,为解决这一问题,近距平行跑道(CSPR)概念应运而生。近距平行跑道是指两平行跑道的中心线间隔小于或等于760m(2500ft)的平行跑道。为发挥近距平行跑道优势,国内外学者主要从碰撞概率以及跑道容量两角度对近距平行跑道进近方式进行研究,提出了近距平行跑道配对进近的概念[1~10]。其中,经典研究如国外学者Jonathan Hammer对实施CSPR时采用偏置进近更有利于避免飞机遭受尾流影响进行实验论证[11];R H.Mayer等利用Monte Carlo进行仿真证明当配对进近飞机斜距为1.5NM时,可以显著提高机场容量[12];M Janic等对采用不同下滑角实施配对仅仅对容量的影响进行分析[13]。国内学者张兆宁、黎新华、王莉莉等对飞机交通流中跟驰模型进行建模[14];邓文祥等对近距平行跑道离场尾流间隔优化进行研究[15];田勇等结合侧风影响对CSPR模式下配对机的离场时间间隔进行探究[16]。
随着导航精度的日益提升,美国联邦航空局(FAA)针对近距平行跑道,提出了全新的配对进近方式——简化配对进近程序(SAPA),其基于等宽导航性能,依赖增强全球导航卫星系统(GNSS)、相邻着陆告警系统(ALAS)、地基增强系统(GBAS)、星基增强系统(SBAS)、精确跑道监控(PRM)和偏置仪表着陆系统(ILS)等提供精准导航。其最大的优势是配对后机可超越前机,即两机可以采用不同的最后进近速度,两机间安全间距也随之增大,为具有不同进近速度曲线的SAPA配对飞机提供了操作灵活性,极大地提高机场运行效率[17~18]。但国内外少有文章对其进近过程及安全区域进行分析。本文考虑人行为误差,导航误差,尾流特性以及侧风对两飞机进近安全间隔影响,结合飞机尾流承受能力,计算两机进近安全区域及危险区域。
2 简化配对进近模型
2.1 配对进近安全区域
配对进近是在仪表气象条件下(IMC)实施的类似于相关平行仪表进近的程序。现阶段近距平行跑道配对进近的间隔标准在飞行时配对后机不可超越前机的条件下,由两架飞机的防撞间隔和尾流间隔确定,即为避免前机错误进近时后机与前机发生碰撞,后机必须与前机保持在最小安全距离以外。同时,为确保在前机产生的尾流到达后机进近航迹之前安全避让尾流,后机须与前机保持在最大安全距离以内,但是防撞边界和尾边界形成的安全区域狭小,且对两机进近速度差有严格要求不利于飞行员操作,而SAPA的提出解决了这一问题。同样在实施SAPA时,两驾飞机配对飞行,其中一架飞机会遭受另一架飞机产生的尾流的影响进而可能造成危险进近。故与近距平行跑道配对进近所形成的安全区相似,SAPA亦定义了自己的安全区——简化配对进近符合区域(SAPA-CZ),其安全区域满足:1)其前界是保证当快机超越慢机之后,快机的尾流不影响到慢机的飞行安全;2)后界保证当快机在慢机之后飞行时,慢机的尾流不会影响到快机的飞行安全。安全区域Ⅰ上下边界均由侧风影响下的尾流横向动运决定,尾流危险区后界即为后机于前机后方避让尾流时所允许的与前机保持的最小距离,与前机尾流消散及后机承受尾流能力有关,故为确定安全区与危险区大小,对尾流特性的研究为本文重点。

图1 简化配对进近安全区域
2.2 简化配对进近过程
管制员负责初始最后进场阶段的飞机配对,两机之间垂直间隔至少为1000英尺,均以3°下滑角进近。最后进近阶段起始于前机以V0匀速飞跃最后进近定位点(FAF)点时,后机于其后S0处以相同速度沿右侧跑道中心延长线均速飞行并实时监测前机运动状态。前机飞越FAF时即刻以a匀减速直至其最后进近速度V1,同时后机检测到前机减速也随即以相同加速度a减速至后机的最后进近速度V2,其中V2>V1,随后两机以各自最后进近速度完成最后进近。起始两机纵向间隔保持不变,当两机减速到V2后,由于后机进近速度大于前机进近速度,故纵向间距不断缩小,若两机速度差足够大,在距跑道入口某处后,随后快机超越慢机,直至快机飞跃跑道入口上方,配对过程随即结束。绘制两机最后进近高度剖面示意图、速度示意图如图2~3。
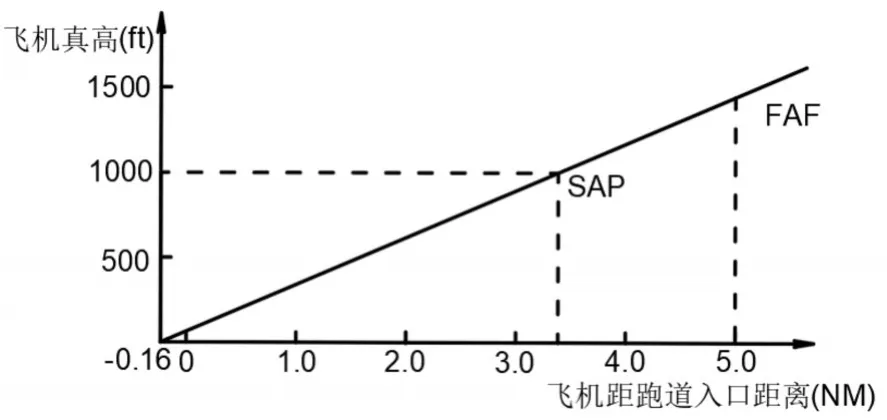
图2 最后进近高度剖面图
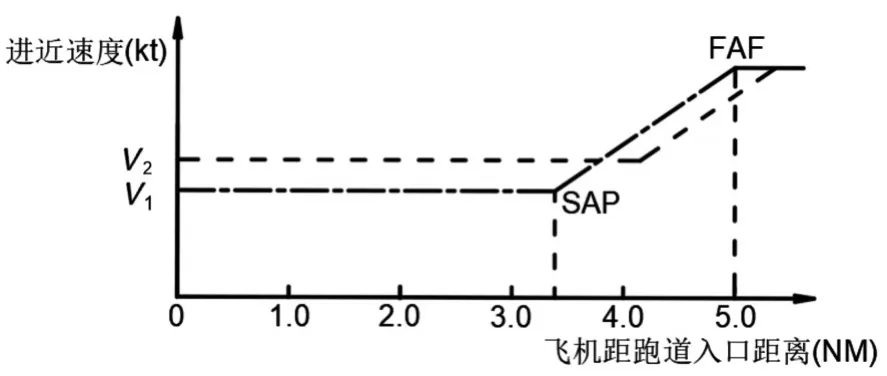
图3 配对飞机进近速度示意图
因实施简化配对进近程序配备先进ALAS系统避免了飞机错误进近至相邻飞机飞行航迹的可能且航空器最后进近时高度差很小[19],故做出如下假设:1)只考虑配对飞机纵向危险接近风险,不考虑垂直方向和侧方向。2)考虑的时间范围为自慢机到达FAF开始,直至有飞机到达跑道入口为止。3)配对进近起始时,快机于慢机的尾流安全区域以内。
配对进近初期后机需要实时监测前机飞行状态,以便当前机开始减速时后机随之做出响应,但由于导航设备延迟和飞行员反应需要额外时间,实际中很难做到同时减速。综上,设快机的起始位置(即慢机后S0处)为参考点,Li(t)为t时刻飞机i(i=1,表示慢机;i=2表示快机)距离该参考点的纵向距离,导航误差和飞行员行为误差造成的减速延迟时间为t1,对两机运动过程进行建模,可得两机之间纵向间距为L(t)=L2(t)-L1(t)若L(t)<0,则快机超越慢机,计算公式如下:

3 尾流特性研究
3.1 尾涡强度模型
航空器飞行过程中,产生升力的机翼上下翼面形成压力差,气流由下翼面流向上翼面,进而在翼尖处形成尾涡。国内外学者已建立了多种尾涡模型,如 Rankine模 型、Lamb-Oseen模 型、Hall⁃ock-Burnham(H-B)模型、Adapted模型、Smooth blending模型、Multiple scale模型等,由于H-B尾涡模型计算简单并能精确描述尾涡的切向速度,因此使用该模型计算尾涡切向速度[20]。其模型如下:
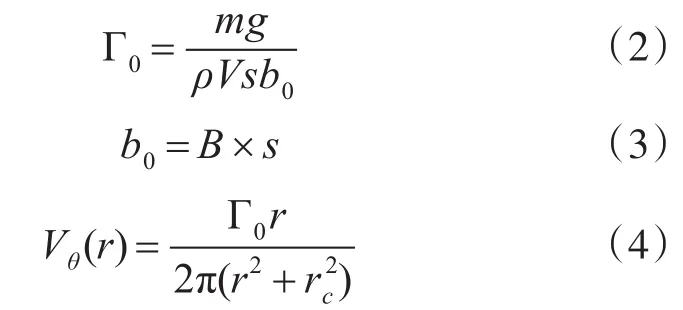
式中:Γ0为尾流的初始环量,m2/s;Vθ(r)为尾涡的切向速度,m/s;m为飞机重量,kg;g为重力加速度,9.8kg/m2;r为尾涡横切面上点与涡核中心点之间的距离,m/s;ρ为空气密度,kg/m3;V为相对于飞机的来流速度,等效于产生尾流飞机的飞行速度,m/s;B为产生尾流飞机的翼展长度,m;r为尾涡横切面上点与涡核中心点之间的距离,m;b0为涡核间距,m;s为机翼压力横向分布系数,取π/4。
3.2 尾涡耗散模型
大气紊流度、温度梯度、风速、分层效应等均对尾流的形成及演变过程造成影响,继而尾流产生消散现象。FAA尾流研究小组基于脉冲激雷达在旧金山国际机场、约翰肯尼迪国际机场、法兰克福机场进行尾涡强度探测,本文对尾流测量数据进行拟合后得出尾流强度衰减模型:
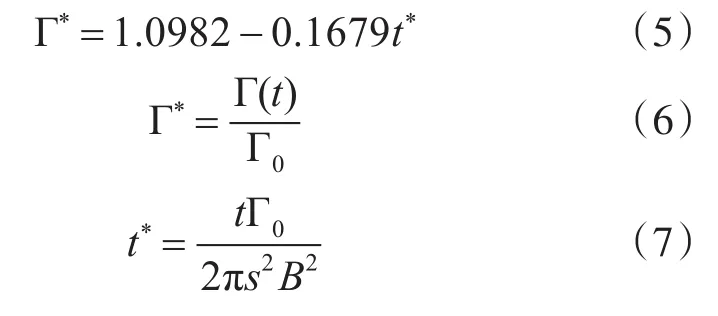
式中:Γ*为无量纲的相对环量,即为尾流实际环量与初始环量之比;t*为无量纲的相对时间,即尾涡耗散时间与基准时间之比。其中,SAPA程序确定安全区Ⅰ后界计算中,尾流耗散时间等效于后机飞至前机产生尾流位置的所需时间,由两机间隔和后机飞行速度决定。随即可得尾涡强度与飞行距离的关系:
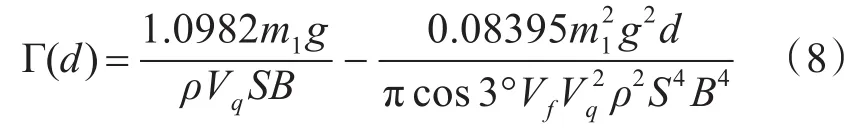
式中:Γ(d)为前机后方一定飞行距离d处的尾涡强度;Vq为前机真空速,m/s;Vf为后机的真空速,m/s。
3.3 尾涡的遭遇模型
当飞机纵向进入前机的尾流涡核中心区域,将受到前机尾流流场中诱导速度的影响。由于两侧机翼受到相反方向的气流作用,飞机将受到尾流诱导滚转力矩,飞机因遭遇尾流后升力不均匀而产生的滚转力矩大小可由下式表示:
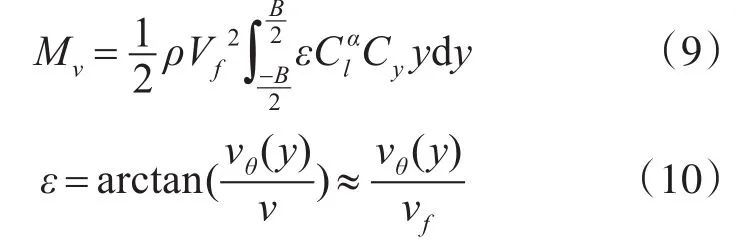
式中,ε为尾流引起的迎角变化量,Vθ(y)尾流诱导下沉速度,m/s;Vf为气流速度,等效于飞机飞行速度,m/s;Cy为弦长;为升力线斜率,使用半翼纵横比和普朗特校正求得,计算公式如下:
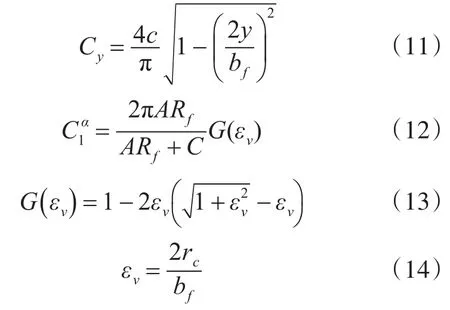
式中,ARf是机翼纵横比;G(εv)是校正函数;C由普朗特积分方程求解后可知取值为4;Ct为翼尖弦长,Cr为翼根弦长。由式(9)~(14)可得诱导力矩计算公式:

由于滚转力矩是尺寸量,难以用于不同机型组合的全局比较分析。故本文采取无量纲滚转力矩系数(RMC)作为尾流遭遇的严重性衡量指标,RMC是一个与飞机飞行速度、翼展以及机翼面积有关的无量纲系数,其与滚转力矩关系如下:
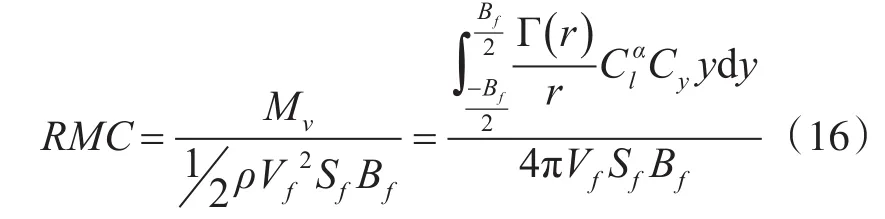
式中,Sf为后机机翼面积,m2;Bf为后机翼展长度,m。可由飞机周围的尾涡强度时,计算出所承受的RMC值,反之亦然,进而可以定量计算不同机型组合下后机于前机尾流后方避免尾流所需安全间距(即危险区域下边界)Mi。
3.4 尾流的侧向移动模型
3.4.1 尾流侧向移动影响因素
在SAPA模式下,为确保两机的尾流互不影响对方进近,飞机须处于安全区域内飞行,而安全区Ⅰ下边界由尾流侧向移动特性决定,即配对前机飞行时产生的尾流,以一定初始宽度在大气湍流、侧风分量以及地面效应的影响下向机身两侧扩散,经过一段时间扩散到另一条平行航迹。
在飞机后面的垂直面上,尾涡可由一对反向旋转涡旋来表示,涡核的初始距离(即b0)与飞机翼展有关,如式(3)所示。随着尾流的生成与扩散,尾流具有一定危险宽度,在可接受安全水平的基础上,计算出不同机型组合的尾涡影响区,横向影响区域宽度也因前后机机型组合的不同而不同。为计算保守尾流安全间隔,选择将不同机型组合的宽度中的最大值作为影响区域的最终宽度,记为Δyi,取值为100m[21]。
当尾流处于静止流体中时,尾涡保持相对平直,进行缓慢下沉及衰减。而当尾涡处于大气环境中时,因湍流流场、飞机部件产生的粘性涡、发动机喷射气流的作用,尾涡会随时间向两侧扩散,间距逐渐增大,计算公式如下:
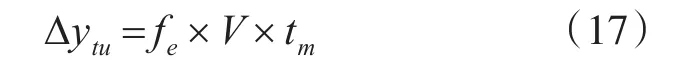
式中:Δytu为湍流影响下的横向扩散区;fe为扩散速率,根据NASA的实验数据,扩散速率为0.02;V为前机飞行速度;tm为尾涡衰减时间。
尾流传播一段时间后,尾涡对将出现crow不稳定性,尾涡对开始经历有规律震荡形成有振幅的长波,振幅受诱导速度场影响,当振幅达到b0的宽度时,旋涡开始出现纠缠和连接,导致旋涡强度迅速衰减。因此,在确定尾流横向影响范围时,取b0为crow不稳定性的影响范围,记为Δyc。
因SAPA程序针对窄间距跑道,侧风分量大小对配对进近安全性产生重大影响。根据NASA对飞行事故统计调查可知,尾流事故多发生在侧风为1m/s~5m/s的环境中。当侧风分量(Vw)小于1m/s时,对尾流侧移无实质性影响;Vw大于3m/s时,过大的风力使尾流迅速消散[22]。而尾流在1m/s~3m/s的侧风分量下会加速向后机航向道运动,继而增大危险区域宽度,记侧风分量引起的尾流横向危险区域为 Δyw:
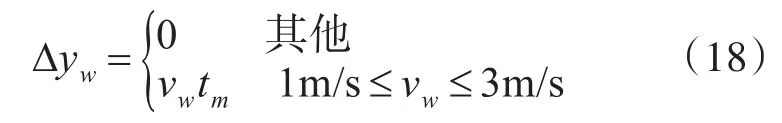
当前机产生的尾流距离地面的高度大于半个翼展小于一个翼展时,尾涡与地面的相互作用。在地面效应作用下,飞机左右两涡在原有扩张的基础上再以2m/s~3m/s的速度向两侧移动,进而增加危险区域宽度,记为Δyg:

3.4.2 尾流侧向移动距离
前机尾流侧向移动距离由航空器性能、侧风、尾流特性、地效等多种因素决定,综上所述,尾流横向移动总距离为
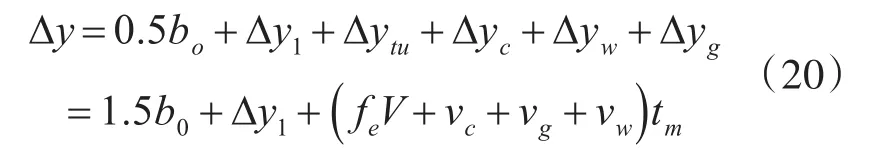
为保证后机于前机产生的尾流前避让尾流,此时Δy需满足;
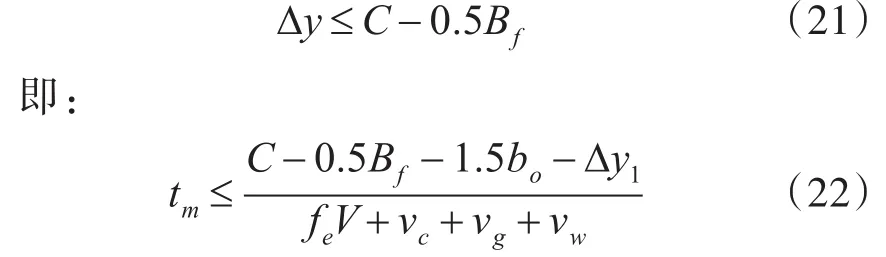
则安全区域Ⅰ下边界计算公式为

同理,安全区域Ⅰ上边界的计算由快机尾流在侧风影响下的横向运动决定,为计算最保守安全区域,假设配对进近过程中总是不利侧风向,将快机进近参数代入式(2)~(19)即可得安全区域Ⅰ上界数值大小。
4 算例分析
某国内国际机场02L/20R与02R/20L跑道间距为380m,为典型近距平行跑道,FAF至THR距离为5NM,对该机场某日进场航空器进行统计,选取当日占比最大的两类飞机A320作为前机、B737-800作为后机进行配对进近,两机配对参数如表1所示。
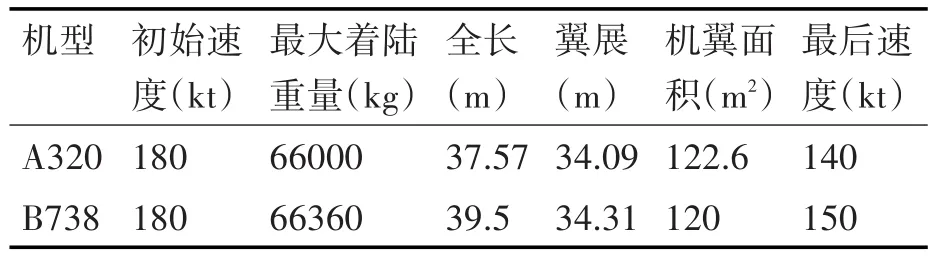
表1 前后机机型数据
两机开始配对进近时,由式(1)计算出A320在该设定条件下得初始尾流环量为260.88m2/s。根据欧控尾流间隔研究,取A320可承受滚转力矩系数为0.045,代入式(8)、(16)、(23)利用Matlab求解得B738可承受尾流环量为145m2/s,前机尾涡耗散到B738承受能力需55.77s,则起始危险区域下边界为后机距离前机5164.3m处。分析最不利条件下的两机间隔大小,故取侧风分量Vm为3m/s,地效影响下尾流侧向速度增加量为3m/s,由式(22)可知尾流侧移到平行航迹的时间为26.96s,代入相关参数计算可知,安全区域Ⅰ下边界为后机距前机2496.5m处,安全区域Ⅰ纵向长为4993m,危险区域纵向长为2667.8m。在该算例中取导航误差和飞行员行为误差造成的减速延迟时间t1为5s,由运动方程计算可知,配对过程中两机均处于安全区域内,符合实际运行情况。而国外现行近距平行跑道配对进近安全区是快机不可超越慢机模型下运行,前界由防撞间隔确定,数值为两机机身长度和一半,代入数据可知该模式下初始安全间隔为2457.97m,对比后可知,实施SAPA极大地提高了两机间安全间隔。
5 结语
尾流是影响近距平行跑道运行的关键因素。本文着重对尾流特性进行研究,探究侧风、大气湍流、地面效应对尾流侧向运动的影响,计算简化配对进近安全区域边界。建立尾流耗散模型,对尾流遭遇严重性衡量指标进行分析,结合后机可承受尾涡环量能力,对配对进近危险区域进行计算。研究表明,与国外部分机场现行实施的近距平行跑道配对进近相比,实施简化配对进近程序对配对两机进近速度要求降低,极大增加安全区域,且依据尾流承受能力对危险区域的计算亦可用于配对单元间的动态尾流间隔缩减,极大提高机场运行安全及效率。
