Improvement of the short-term stability of atomic fountain clock with state preparation by two-laser optical pumping*

Lei Han(韩蕾), Fang Fang(房芳), Wei-Liang Chen(陈伟亮), Kun Liu(刘昆),

Shao-Yang Dai(戴少阳)2, Ya-Ni Zuo(左娅妮)2, and Tian-Chu Li(李天初)1,2,‡

1School of Optics and Photonics,Beijing Institute of Technology,Beijing 100081,China

2Key Laboratory of Time and Frequency Standards,National Institute of Metrology(NIM),Beijing 100029,China

Keywords: optical pumping,atomic fountain clock,spin-polarization,short-term stability

1. Introduction

The cesium fountain clocks are used as primary frequency standards (PFSs) to realize the definition of the SI second,which have been widely used in calibrating the time scale,frequency metrology, tests of fundamental physics, etc.[1–3]The total uncertainties of the state-of-the-art fountain clocks have reached a few parts in 10−16.[4]The relative frequency stability (type-A uncertainty uA), which is usually limited by local oscillator phase noise,is a major component to the total uncertainty. Taking advantage of a cryogenic sapphire oscillator, Bize et al. in BNM-SYRTE reduced the relative frequency stability down to 1.6×10−14τ−1/2,which was limited by quantum projection noise.[5]An optically stabilized microwave oscillator(OSMO)has also been used as a local oscillator for atomic fountains, acquiring a relative frequency stability of 2.5×10−14τ−1/2for CSF2 fountain in Weyers group in PTB.[6]Optical pumping (OP), redistributing atomic populations among the hyperfine-structure levels by selective absorption of lights, has attracted extensive attention in atomic physics and related fields, such as atomic clocks and atomic magnetometers.[7,8]Generally, circularly polarized lights are used as OP for noble-gas nuclei in the field of magnetic resonance imaging and for alkali atoms in atomic orientation and magnetic resonance to accumulate more atoms in the stretched state.[9,10]And now,OP has also been used in the atomic fountain clocks with π-polarized laser to accumulate atoms in the|mF= 0〉 state.[11–15]A theoretical model of evaluating the pumping efficiency,taking into account of ground and excited states structures,Zeeman coherences,neighboring transitions,and laser field fluctuations, has been presented in Ref. [16].The similar experiments have been described in Ref. [12] by collecting atoms with a magneto-optical trap(MOT)and in the Ref. [15] by collecting atoms with an optical molasses (OM)in atomic fountain clocks.

In this paper, based on the work of Ref. [12], we further demonstrate the theoretical analyses about the limitations of the stray magnetic field, the purity of the OP light polarization, and the asymmetry of σ+/σ−components to the OP efficiency. Then the OP is implemented experimentally to increase the atom population in the |F =4, mF=0〉state,and improve the frequency stability of the fountain clock NIM6,which used an optically generated microwave as the local oscillator.[17–21]The improvements of signal-to-noise ratio(SNR)under different conditions are presented,and the influence of different dead times on the relative frequency stability due to the Dick effect is also shown at the end.

2. Theoretical analysis and experiments

2.1. Theoretical simulations

Ideally, a linear polarized laser with its polarization direction aligned with the direction of the magnetic field is applied to drive the |F =4〉→|F′=4〉 transition. The forbidden transition of |F =4,mF=0〉→|F′=4,mF′ =0〉 leads to a population accumulation in the|F =4,mF=0〉state. In this circumstance, the purity of OP light polarization, the coincidence between the magnetic field direction and linear polarization direction of laser beams are the limiting factors to OP efficiency. Here the time evolution of atom populations on each sublevel is analyzed by assuming weak intensities of the OP and repump lights in the presence of the residual magnetic field on the horizontal plane and the imperfection of the OP laser polarization. The population evolution including|F=4〉→|F′=4〉and|F=3〉→|F′=4〉transitions is given by[22]

where Nei, Nfk, and Ngldenote the populations of the different hyperfine sublevels. And the subscript e represents the excited-state |F′= 4〉, while g and f represent the groundstates |F =4〉 and |F =3〉, respectively. The subscripts i, k,and l represent the Zeeman levels for each hyperfine level.The coefficient W is the stimulated emission or absorption rate,which is expressed by the spontaneous emission rates with the following equation:[22]

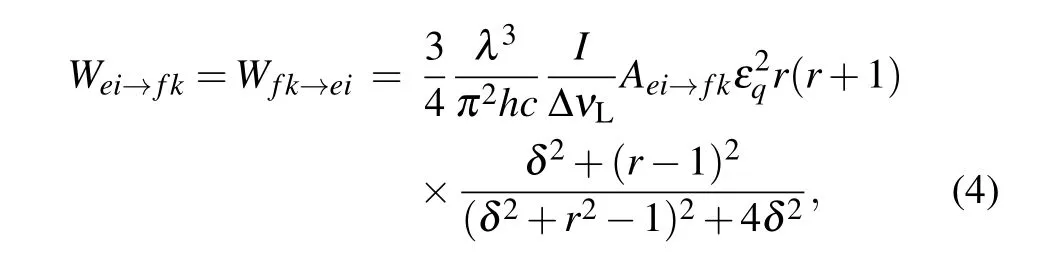
where h is the Planck’s constant,c is the light speed in vacuum,and λ is the laser wavelength. I is the laser intensity and ΔνLis the laser linewidth. The spontaneous emission rate between sublevels ei and fk is Aei→fk=aei→fkΓ. Γ is the spontaneous emission decay rate. aei→fkis the dipole matrix elements for transitions.[23]εqrepresents the components of σ+, σ−, and π polarization with the subscript q taking the values of +1,−1,and 0. r=2πΔνL/Γ represents the ratio of the laser and atomic linewidths and δ =4π(νA−νL)/Γ denotes the detuning of the laser frequency from the atomic resonance.

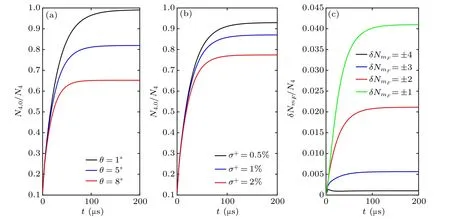
Fig.1. Build-up of the atom population in the|F =4,mF =0〉sublevel for symmetrical and asymmetrical σ+/σ−transitions. (a)Build-up of atom population in the|F=4,mF =0〉sublevel during the OP pulse for different θ angles with an atomic cloud size of R=5 mm.(b)Build-up of the atom population in the|F =4,mF =0〉sublevel for the asymmetrical σ+/σ−transitions with different percentages of σ+ components.(c) Build-up of atom population asymmetry between |F,±mF〉 sublevels with 1% of σ+ component, and δNmF =(N4,+mF −N4,−mF). The black,blue,red,and green lines respectively represent the atom population asymmetries of mF =±4,±3,±2,and±1.

The density distribution of the atomic cloud is a 3D Gaussian distribution with a radius of R as expressed in Eq.(3),

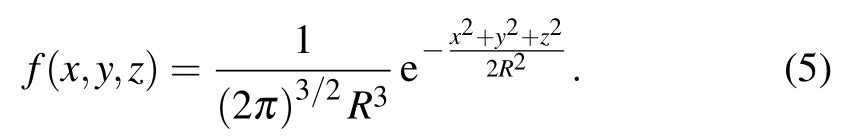
The orthogonal coordinate system is established with the incident direction of the OP laser as the x-axis, the direction perpendicular to it on the horizontal plane as the y-axis,and the vertical direction as the z-axis (see Fig. 2(a)). Besides a uniform magnetic field Bzapplied along z-axis to define the quantization axis, a residual magnetic field Bron the horizontal plane could also present due to an imperfect bias field. Thus,the clock state|F =4,mF=0〉will not be a dark state anymore,and symmetrical σ+/σ−transitions will be excited even with a pure linear polarization OP light along the z-direction. When the magnetic field direction is in the perpendicular plane of the incident laser with a tilt angle θ to the z-axis,the ratios between different orthogonal(σ–π)polarizations are defined as σ+:π :σ−=sin2θ :1:sin2θ. And the polarization impurity of the OP laser limited by the extinction ratio of the polarizing beam splitter(PBS)is defined as the proportion of the σ-polarized laser component that will also bring about symmetrical σ+/σ−transitions. A common PBS with the extinction ratio of 30 dB will introduce 0.1%σ-polarized component,equivalent to a tilt angle of 2°(sin2(2°)=0.1%).As the magnetic field has a component along the x-axis, the symmetrical σ+/σ−transitions will also be excited, also reflecting the pitch angle of the laser incident direction. If the laser after passing through PBS has a circular polarization component, the asymmetrical σ+/σ−transitions will be excited. Here only the σ+transition is simulated as an example(similar to σ−transition).

With a typical atomic cloud size of R=5 mm in our experiment,the atom populations in the|F=4,mF=0〉sublevel under different OP interaction durations for different angles θ are calculated, where θ represents the tilt angle between the linear polarization direction of the laser beams and the magnetic field direction in the y–z plane (without x component).This simulation also applies to the polarization impurity cases.In Fig.1(a),the black,blue,and red solid lines indicate θ=1°,θ=5°, and θ=8°(namely, the percentages of σ component equal to 0.03%, 0.76%, and 1.90% as sin2(θ) =σ%) with|F =4,mF=0〉 populations up to 99%, 82%, and 65%, respectively. As to the asymmetrical σ+/σ−transition,we calculate different components of σ+transitions corresponding to that σ+equals to 0.5%,1%,and 2%,respectively(without σ−transition). And the |F = 4,mF= 0〉 populations raise from 11% to 93%, 87%, and 77%, respectively, as shown in Fig. 1(b). The asymmetry population between |F,±mF〉sublevels is defined as (N4,+mF−N4,−mF)/N4. The asymmetry curves of four pairs of sublevels are depicted in Fig. 1(c)for the σ+= 1% case, with an imbalance of 4% between|F =4,mF=±1〉states as the worst case.

The Allan standard deviation of the relative frequency stability of an atomic fountain clock can be expressed as[24–26]

3. Experiments

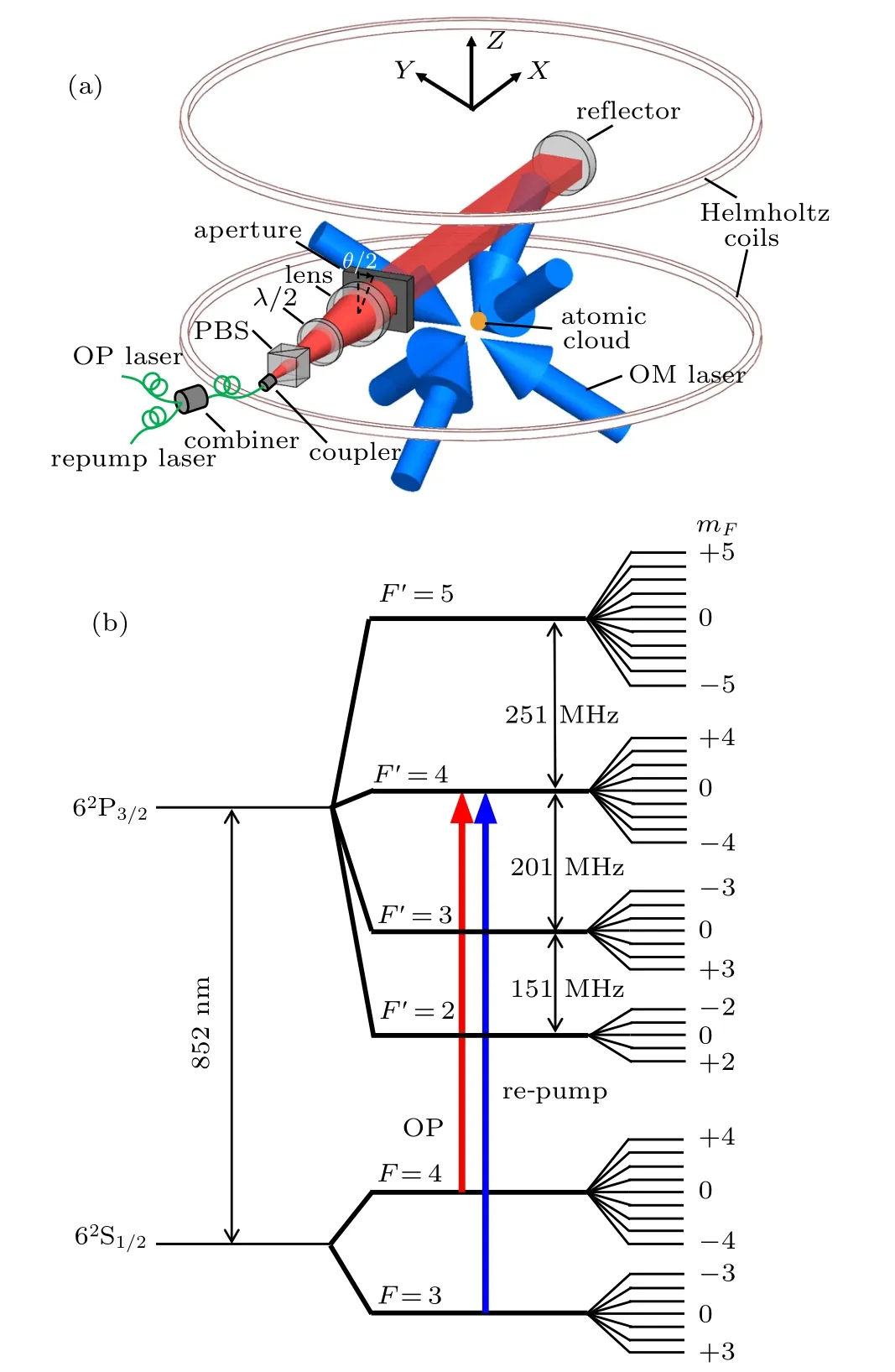
Fig. 2. (a) Simplified experimental configuration: the atom cloud (orange) launches up along the z-axis. Three pairs of orthogonal cooling lasers (blue) counter-propagate in the OM region. The OP laser (red)and repump laser (red) coincide with each other and propagate along x-direction. A pair of Helmholtz coils (white rings) with a radius of 180 mm and a distance of 140 mm provides the magnetic field to define the quantization axis. (b) The hyperfine structure of cesium D2 transitions. The red and blue lines separately denote the OP and repump lasers resonant with|F=4〉→|F′=4〉and|F=3〉→|F′=4〉transitions. The energy gaps are not in scale.

The experimental configuration is shown in Fig. 2. The OP and repump beams are combined and propagated along the x-axis and interact with the atoms at the region 32 mm above the center of the OM region. The OP laser and repump laser are injected into the same polarization-maintaining fiber and the OP laser power is limited to 300 µW while the repump laser power is about 200 µW. Then the beam passes through a polarizing beam splitter(PBS)and a λ/2 plate,with its polarization adjusted to be linear along the magnetic field direction. The estimated impurity of the laser polarization due to the PBS is about 0.2%in our experiment, corresponding to a tilt angle of 2.5°. The beam is retro-reflected,forming a standing wave field. The OP laser is tuned close to the resonance of the |F =4〉→|F′=4〉 transition with a π-polarization to ensure the|F =4,mF=0〉being a dark state according to the angular momentum selection rules. Thus, the population of|F =4,mF=0〉builds up. Another π-polarized laser on resonance with the|F=3〉→|F′=4〉transition is used to repump the atoms back to the|F =4〉state from the|F =3〉state(see Fig.2(b)). A pair of Helmholtz coils with its center coinciding with the OP beam center is employed to generate a uniform magnetic field along the z-direction.

All the atoms are populated in the|F=4〉hyperfine state and approximately evenly distributed in each Zeeman sublevels after launching. Then the OP and repump beams are applied to accumulate atoms in the|F =4,mF=0〉state population. A microwave pulse is applied following to transfer the atoms from the |F =4,mF=0〉 state to |F =3,mF=0〉state. Next, the residual atoms in the |F =4〉 states are removed by a traveling-wave laser beam on resonance with the|F =4〉→|F′=5〉transition. Thus,a pure clock state is prepared,and a Ramsey transition can be applied afterwards. The atom populations in |F =3〉 state and |F =4〉 state are detected as N3and N4separately, and the transition probability P=N4/(N3+N4)is acquired.

4. Results and discussion

A Rabi type π-pulse microwave is applied to excite the|F =4〉→|F =3〉,ΔmF=0 transition,and the atom populations in the |F =4〉 state and |F =3〉 state are detected separately. The transition probabilities for different microwave field detunings denote the atom populations of |F = 4,mF〉states,whereas the|mF=±4〉states cannot be measured. After optimizing the OP/repump laser intensities, frequency detunings, polarizations, and the magnetic field density magnitude and direction,a population of 63%of|F=4,mF=0〉has been achieved as plotted in Fig.3.

Compared with the results of other research group,[12,15]the population accumulated in the clock state is limited by the pitch angle of the laser incident direction and the noncoincidence of the incident and reflected beams, resulting in an estimated OP efficiency up to 90%. The impurity of the laser polarization of 0.2% and the stray magnetic field make a further 80% reduction of the OP efficiency due to the large atomic cloud, which is more sensitive to the magnetic field distribution. Other factors, such as the nonuniform distribution of the magnetic field on the horizontal plane,will also set a constrain on the OP efficiency. Besides the above effects,the OP efficiency will also be limited by the reabsorption of un-polarized light emitted from the atomic cloud as shadow effect.[11]This effect is checked by varying the atom numbers with different loading times and the detected atoms are compared with the atom numbers obtained without OP. The factors of 4.4,4.2,and 4.1 increasements are obtained for low,medium(2.5-fold),and high(5-fold)atomic densities,indicating this shadow effect.

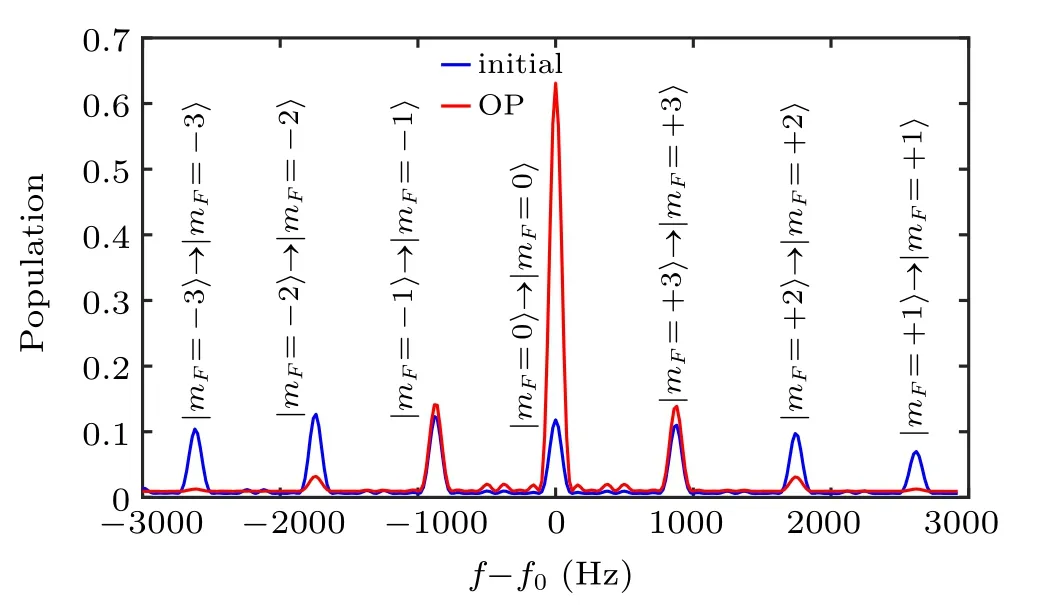
Fig. 3. The populations on mF sublevels with (red line) and without(blue line)OP measured with microwave spectra.The peaks correspond to populations on each|F =4,mF〉state(|mF =±4〉not shown).

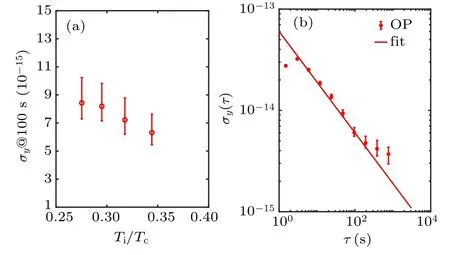
Fig. 5. (a) Plot of the short-term stability of the cesium fountain at 100 s over the ratio of total Ramsey interrogation time Ti to cycle duration Tc. (b)Allan standard deviation σy(τ) with OP of NIM6 at the same cycle time 1.5 s.

For a Cs fountain clock, more atoms will introduce a larger collisional frequency shift, and the largest number of atoms is not always the optimum. With OP, the same atom number can be obtained with a reduced fountain cycle, leading to an increasement of the duty cycle, corresponding to a smaller Dick effect.[28]This effect on the stability of the fountain clock is verified by obtaining the same atom population with different loading times. And the short-term instabilities of a fountain clock decrease as the ratio of Ramsey interrogation time Tito cycle duration Tcincreases as shown in Fig.5(a),which is consistent with the result in Ref.[29].

5. Conclusion and perspectives

In summary, the influence of the residual magnetic field and the purity of OP laser polarization on the OP efficiency is theoretically analyzed. Moreover,it has been demonstrated that the optical pumping process improves the short-term stability of the atomic fountain clock in terms of shortening the cycle time or increasing the atom number. The short-term stability will be further improved with a better detector,stabilizing the detection laser intensity and reducing its linewidth.