Cold atom clocks and their applications in precision measurements*

Shao-Yang Dai(戴少阳), Fa-Song Zheng(郑发松),2, Kun Liu(刘昆), Wei-Liang Chen(陈伟亮),Yi-Ge Lin(林弋戈), Tian-Chu Li(李天初), and Fang Fang(房芳),†

1National Institute of Metrology(NIM),Beijing 100029,China

2The State Key Laboratory of Precision Measurement Technology and Instruments,Department of Precision Instrument,Tsinghua University,Beijing 100084,China

Keywords: atomic fountain clock,optical clock

1. Introduction

Over the last three decades,theoretical and technical advantages in laser cooling and trapping of atoms,[1–3]optical frequency combs,[4–6]and quantum controls[7,8]boosted their applications in precision measurements,and achieved extraordinary accomplishments. With atoms being cooled down to μK or even lower temperatures, atomic motions and states can be precisely manipulated. Thus, the Doppler effect can be largely reduced and the coherence time can be extended much longer, leading to orders of magnitudes of improvement in precision measurements. Cold atomic interferometers have demonstrated outstanding performances in the rotation and acceleration measurements. They have been widely used not only in gravity,[9]gravity gradient,[10]and rotation measurements,[11,12]but also in the tests of Einstein’s weak equivalence principle,[13,14]and measurements of fundamental physical constants.[15,16]Cold atoms also provide ultrastable oscillators that can be used as frequency standards. Of all measurement quantities,frequency can be determined with the highest degree of accuracy. Apart from generating time scales,frequency standards offer a wide range of applications from the measurements of other quantities such as length,electric current,etc. to the tests of fundamental physics principles.Time and frequency also play a vital role in the navigation systems,network synchronization in the telecommunication field,etc.Today,the cesium(Cs)and rubidium(Rb)atomic fountain clocks have achieved an accuracy of a few parts in 1016,[17–25]while the type B uncertainty of the best optical clock based on single Al+ion has been lowered down to the 10-19region.[26]In parallel, the state of art manufacturing technologies with the development of smaller and robust while much cheaper electronic components,have extended the applications of frequency standards to much wider areas.[27–29]

In this paper,we focus on the recent developments in the high-performance atomic clocks which can be used as the frequency standards to calibrate atomic time scales. A brief history of atomic clocks is introduced in Section 2. The basic principles, performances, and limitations of fountain clocks and optical clocks based on trapped single ions or multi atoms are introduced in Sections 3 and 4,respectively. Section 5 introduces the frequency measurements and comparisons of optical clocks. In Section 6, the proposals and requirements for the future redefinition of the SI time unit second are presented.The applications of atomic clocks in the study of fundamental physics and everyday life are summarized in Section 7, and the summary is given in Section 8.

2. A brief history of atomic clocks

Atomic frequency standards(AFSs)are instruments providing accurate frequency signals. Amount many kinds of AFSs, primary frequency standards (PFSs) realize the definition of the Syst`eme International (SI) unit “second”. From Cs beam clocks to Cs fountain clocks,the uncertainties lower down from 10-10to 10-16. There are also 9 atomic transition frequencies recommended by the consultant committee of time and frequency (CCTF) as the secondary representations of the second (SRS). Besides Rb atomic hyperfine transition,the other 8 transitions are in the optical frequency region.

2.1. From Cs beam clocks to atomic fountain clocks

Since the definition of the SI unit of time,the second was changed from the astronomical one to the atomic transition in 1967. Cs atomic clocks have been used as the primary frequency standards to realize the definition. The first Cs beam clock developed by Essen and Parry in 1955 reached a relative frequency uncertainty of a few parts in 109.[30]In the 1950,Zacharias explored the first experiment of fountain principle with a thermal atomic beam.[31]In 1989, Kasevich demonstrated a first laser-cooled Na fountain clock.[32]Dr Clairon’s group developed the first Cs fountain clock in 1995 with a fractional frequency uncertainty of a few parts in 1015.[33]Since 2016,11 fountain clocks and 5 optical clocks from 8 countries contributed to the TAI,as shown in Fig.1.The total uncertainties of best fountain clocks have achieved a few parts in 1016.Some other Cs fountain clocks are also under developing and aiming to contribute to TAI.[35–39]

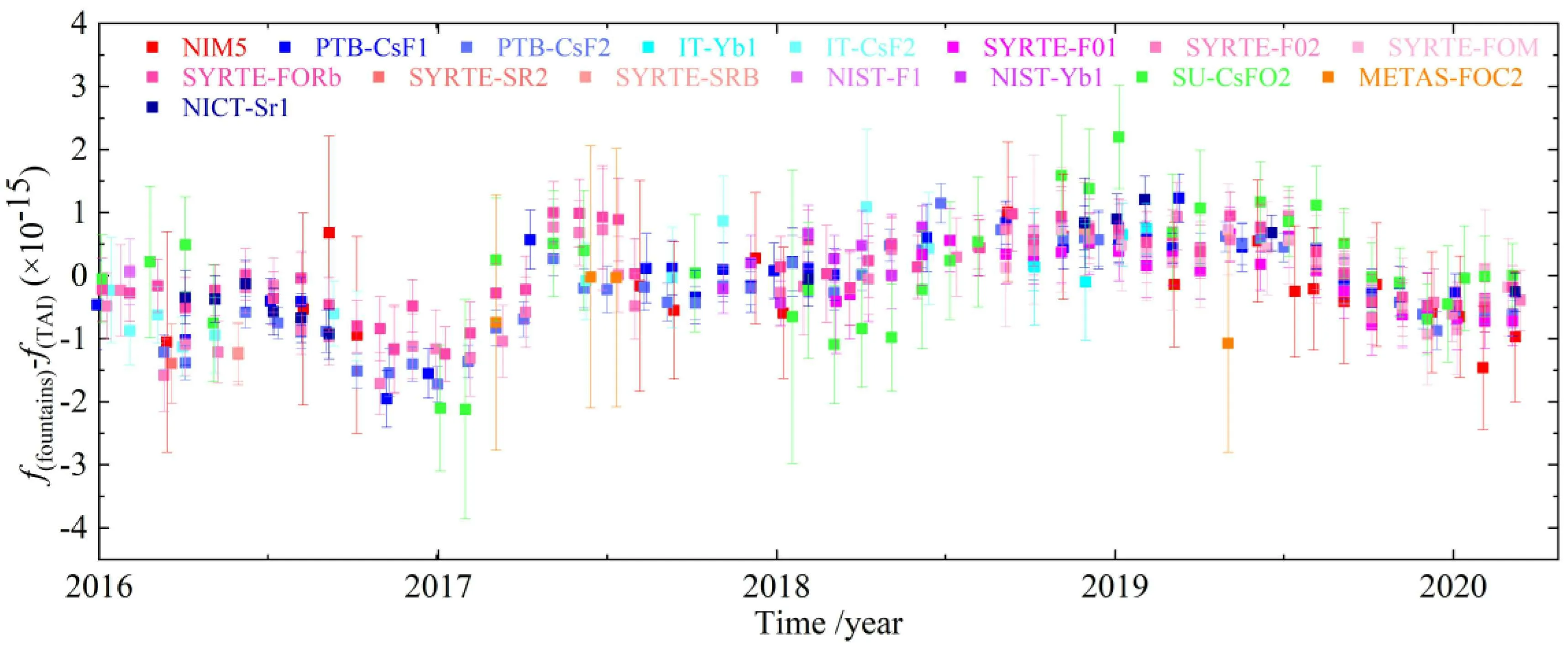
Fig. 1. Evaluations of fountain clocks published on circular T since Jan.2016.[34]

Although the basic designs are similar,some special techniques have been used for different fountain clocks to achieve a better performance. To reduce the blackbody radiation induced frequency uncertainty, the whole physical packages of the NIST-F2 and IT-CsF2 fountain clocks are surrounded by a cryogenic liquid cylinder (80 K). NIM6 fountain clock has a heat pipe made of a thin glass tube filled with pure water surrounding the flight tube to make the temperature more uniform and reduce temperature fluctuations.[40]

METAS-FOC2[41]is a continuous fountain to eliminate the Dick effect and improve its instability. However, a microwave cavity with two distinct interaction zones has to be used,resulting in a larger microwave power-related frequency uncertainty. In addition,light shift cannot be vanished easily,since lasers used for preparing and detecting atoms need to be on all the time.

Rb hyperfine transition is one of the secondary representations of the second. Due to its much lower cold collision frequency shift compared with Cs atoms and more robust cooling lasers, Rb fountain clocks are used not only for calibrating TAI,[42]but also for steering H-masers directly and in the clock ensemble to generate free atomic time (EAL).[43]Four Rb fountain clocks developed by United States Naval Observatory(USNO)have been reported to BIPM since 2012 and the long-term instability reached 5×10-17, the results published on circular T are shown in Fig.2. There are also commercial Rb fountain clocks with a compact design and autonomous operation.[44]

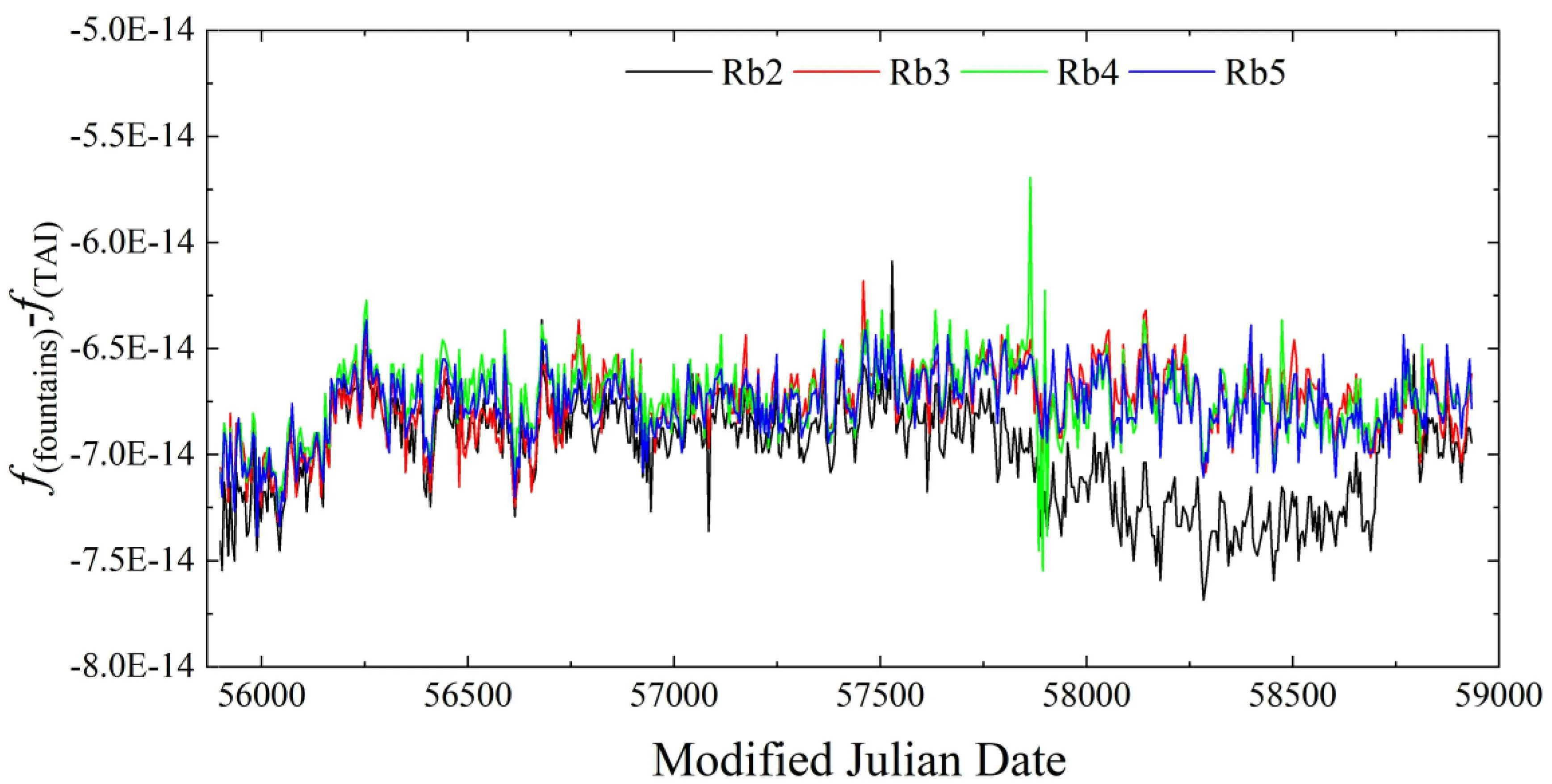
Fig. 2. The data published on circular T since 2012 of four Rb fountain clocks developed by USNO.

Beside fountain clocks, there are also some other cold atomic microwave frequency standards such as Rb-clock developed by Spectra Dynamics Inc,[45]whose size is about that of a desktop computer and the frequency instability of less than 3×10-15has been achieved in one day.Cold CPT clocks promise improved accuracy and instability over existing commercial CPT clocks with room temperature atoms.[46,47]Microwave frequency standards based on cooled ions have also been studied.[48]

2.2. The development of optical clocks

Compared with microwave frequency standards, optical frequency standards have lower fractional frequency instabilities due to their operating frequencies about 4 orders higher than that of microwave frequency standards. Since the development of ion traps, the idea of using trapped single ion as optical frequency reference was proposed by H. G. Dehmelt in 1973.[49,50]However, accurate measurement of an optical frequency was extremely difficult. In 2000, the development of optical frequency combs (OFC)[51,52]linked optical frequency with microwave frequency directly, and made optical frequency measurements much easier. Soon after,the frequency instability of 7×10-15at 1 s was obtained in NIST with a Hg+optical clock.[8]In 2010,the type B fractional frequency uncertainty of an Al+optical clock in NIST reached 10-18range[53]and reduced down to 10-19range in 2019.[26]In addition, the systematic uncertainty of the Yb+optical clock in PTB reached 3.2×10-18in 2016.[54]Since optical clocks with neutral atoms trapped in an optical lattice at magic wavelength were proposed by Katori et al.,[55]optical clocks have made significant progress in recent years.[56–71]The instability of the Yb optical lattice clock in NIST reached to 10-18range in 2013.[72]In 2015, the uncertainty of a Sr optical lattice clock in JILA reached 2.1×10-18.[73]At present,the largest contributions for the type B uncertainty of ion optical clocks come from blackbody radiation(BBR)[74]and excess micromotions.[26]And the largest contributions for the type B uncertainties of optical lattice clocks come from BBR and ac-Stark effect.[73]Furthermore, multi-ion optical clocks and heavily charged ion optical clocks have been proposed for even better instability and uncertainty.[75,76]Meanwhile,more robust and transportable optical clocks have been developed due to a highly demand of the directly optical clock comparisons.[77]

In 2016,the LNE-SYRTE reported the frequency data of Sr optical lattice clock to the BIPM and aimed to participate in calibrating TAI.[78]Since then,another 4 optical lattice clocks in four countries[76,78–81]contributed to TAI[34]as shown in Fig.1.

3. Operation of a fountain clock

Figure 3 shows a typical simplified set-up of an atomic fountain clock.[82]It consists of a physical package (not all components shown), a laser-optical bench(not shown), a microwave synthesizer chain,and an electronic control unit.

Fig. 3. The schematic of an atomic fountain clock. Atoms are captured in a magnetic optical trap(MOT)and launched up. All the atoms are pushed away expect for that in the clock state. They interact with clock signal during the ascending and descending twice to realize a Ramsey interrogation.Transition probabilities are measured and the error signals are sent to lock the clock frequency.

The laser-optical bench provides all the lasers needed for manipulating atoms including cooling, trapping, launching,state preparing and detecting of the atoms. The microwave synthesizer chains provide two microwave signals for stateselection and Ramsey interrogations, respectively. A lowphase-noise local oscillator(LO,usually an ultra-stable crystal oscillator) is used to generate the clock transition frequency via a synthesizer chain and fed into the Ramsey cavity for Ramsey interrogations.Cold atoms are captured in the cooling zone and launched up,and then prepared in the clock state after passing through the state-selection zone. The resonance frequency of a Ramsey cavity with a Q factor higher than 10000 is tuned to the clock transition within a few hundred kHz. Atoms interact with the microwave in the Ramsey cavity twice during the ascending and descending to realize a Ramsey interrogation process.

3.1. Loading and launching of cold atoms

Atoms are captured and cooled in either a threedimensional (3D) magneto-optical trap (MOT)[83]or optical molasses (OM),[1,84]both of which can share the common configuration consisting of three mutually orthogonal pairs of counterpropagating laser beams with a “0 0 1” or a “1 1 1”configuration.For collecting more atoms to obtain a better signal to noise ratio,three methods have been proposed and used including a 2D MOT loading optical molasses,[18]3D MOT loading optical molasses,[40]and optical pumping.[85]With the first two methods,a large number of cold atoms can be captured in the molasses region while still keeping a high vacuum to minimize background gas perturbations in the detection signal and the contamination of the interrogation.Compared with 2D MOT loading OM,a 3D MOT loading OM has a more uniform atomic density distribution. Moreover,the cooling lasers for 3D MOT and OM are required at different time, and one laser can provide all the cooling beams. The Cs energy levels and required laser frequencies are shown in Fig. 4. After the MOT/OM stage, atoms are launched up through a moving molasses[86]and further cooled down to a few μK. Then,all lasers are switched off, and the atomic cloud follows the trajectories of a ballistic flight.

Fig. 4. Energy levels of 133Cs. The excitation lines for optical pumping,cooling/detection,and repumping are indicated by dotted arrows.

3.2. State selection

Atoms are evenly distributed among Zeeman sublevels of the upper hyperfine group state after launching. To obtain a better Ramsey fringe contrast, the atoms are usually prepared in the clock state via “microwave-laser state selection”. For a133Cs fountain clock, the atoms in the state|F =4,mF=0〉 are transferred to the |F =3,mF=0〉 state by a microwave pulse in the state-selection cavity. The remaining atoms in |F =4,mF／=0〉 are removed by applying a radiation pressure from the pulsed detection beam which is tuned to the |F =4〉→|F′=5〉 transition, and the atoms in the clock state are left for the clock frequency measurement.

3.3. Ramsey interrogation and detection

The launched atoms interact with the microwaves in the Ramsey cavity (cylindrical TE011microwave cavity) during the ascending and descending twice, completing a Ramsey interrogation.[87,88]The atom populations in the two ground hyper-fine states are detected and the transition probability p is calculated from[88]

A typical Ramsey fringe of a fountain clock is shown in Fig.5.

Fig. 5. Typical Ramsey fringes of NIM6 fountain clock with a frequency scanning step of 0.1 Hz and no averaging. The inset shows the central Ramsey fringe with FWHM width of 0.98 Hz.

In a routine operation,the frequency of the interrogating microwave is toggled between the two opposite sides of the central Ramsey fringe. The transition probability difference between on two sides of the fringe, provides the error signal to steer the frequency of the interrogating microwave to the frequency of the central Ramsey fringe.

3.4. Fountain clock evaluations

The uncertainty of atomic clocks consists of type-A and type-B uncertainties. Type-A uncertainty represents instability of a clock, usually expressed as the Allan deviation, and can be written as[22,23]

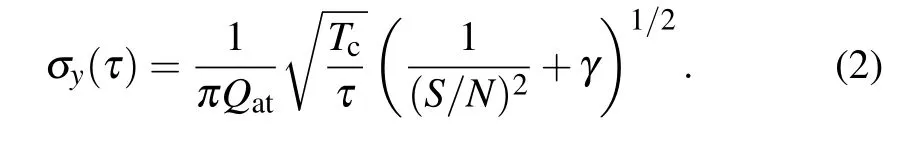
Here, Tcis the duration of a fountain cycle, γ denotes a local oscillator (LO) phase noise, and Qatis the atomic quality factor. The S/N includes the quantum projection noise limited by the number of atoms and detection noise. For a white frequency noise, the instability drops as a square root of the measurement time. When enough number of atoms are detected, the short-term instability of a clock is limited by the phase noise of the LO. With an ultra-stable crystal oscillator, an instability of (1–2)×10-13/τ-1/2can be achieved.To improve instability further, cryogenic sapphire oscillator(CSO)[89]and ultra-stable microwave (USMW) source have been used as a LO.[90,91]Both of CSO and USMW can easily achieve an instability of a few parts of 1015in 1–100 s. With an USMW as LO,the instability of PTB-CsF2 fountain clock reached 2.5×10-14(τ)-1/2when measured by an ion optical clock.[17]

All physical effects that shift a clock frequency should be evaluated and their uncertainties are included in type-B uncertainties. If the physical effects are independent, the total uncertainty should be the square root of the sum of square of each uncertainty component as shown in Eq.(4)[82]

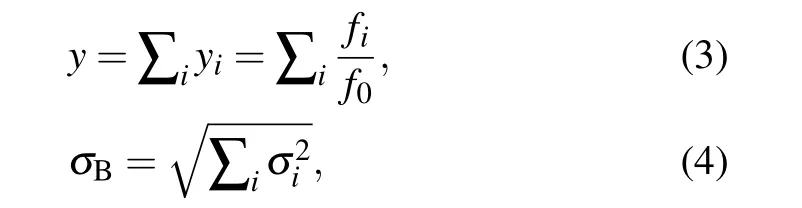
where y is the relative frequency difference, i is each physical effect that may shift clock frequency, f is the reference frequency (9 192 631 770 Hz), fiis the frequency difference relative to the reference frequency caused by each physical effect,σBis the total uncertainty of the clock,and σiis the uncertainty of the frequency difference caused by each physical effect. For a fountain clock, the main effects include secondorder Zeeman effect, cold atomic collisional shift, blackbody radiation (BBR), microwave power related frequency shift,cavity pulling,Majorana transition,gravitational redshift,light shift,second-order Doppler effect,background gas collisional shift, Rabi and Ramsey pulling, etc.[92]Besides, there are other frequency shifts such as microwave lensing, dc Stark shift,and Bloch–Siegert shift,[92–94]all these are estimated to be less than 1×10-16or even lower, and negligible compare with dominate frequency shifts. The major contributions to the total uncertainty published on circular T are listed below in Table 1. Only the best fountains from each lab are included in the table.

Among them,the largest contributions to the total uncertainty are collisional shift and microwave-power related frequency shift.

Table 1. Major contributions in type B uncertainty of a typical evaluation(×10-16).

3.4.1. Collisional shift

The collisions between cold atoms introduce a frequency shift, which is a major contribution to the total uncertainty of a Cs fountain clock. While for a Rb fountain clock, this effect is at least 30 times smaller.[45]The collisional shift is proportional to the averaged density. Thus,in a routine operation,a Cs fountain clock working at two different atom densities alternatively,and the frequency at zero density is deduced from[99]

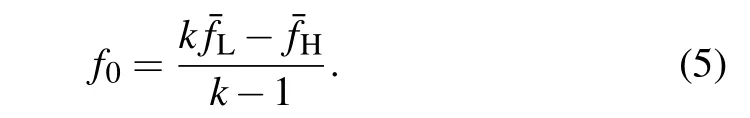
Here k is the ratio between the high and low densities(nH/nL),and fHand fLare the measured frequencies at the two densities,respectively. The uncertainty in eliminating the collision frequency shift is derived from Eq.(5)as[101]

Here, σL, σHare instabilities at the low and high densities,and σkis uncertainty of the ratio k, which includes the nonlinearity between the measured atom numbers and the actual average density as stated in Refs. [20,102]. The last term is treated as the type B uncertainty induced by cold atom collisions.Increasing the ratio k between the high and low densities will reduce this term. Another way is to reduce nonlinearity coefficient σk. Adiabatic fast passage was adopted to reduce the atomic cloud density to exactly half of the high density and the σkdrops more than an order of magnitude compared with a routine method of selecting atoms with a constant frequency microwave pulse.[103]Besides the above two methods,reducing collisional frequency shift(fL-fH)will also reduce its uncertainty. Capturing cold atoms in an optical molasses with a much lower atomic density[99,104]is one way to reduce the collisional frequency shift. Another method is to operate Cs fountain clocks at the optimal proportion of the two clock state populations after the first Ramsey pulse to make sure the collisional rates for two clock states |3,0〉 and |4,0〉 have opposite signs and cancelled with each other, and resulting a much lower collisional induced frequency shift.[105]From Table 1,it is found that this term can be reduced to be less than 1×10-16.[106]

3.4.2. Microwave-power related frequency shift

The microwave-power related frequency shift is introduced by three possible sources: the microwave leakage,the microwave spectral impurity, and the Ramsey cavity distributed phase (DCP).[99,107]Besides a careful sealing of a Ramsey cavity with indium to reduce the microwave leaked out,a Mach–Zehner interferometric RF switch can be added in the microwave synthesizer chain to switch off the microwave when atoms are outside of the cavity. The relative phases of two Ramsey pulses can be measured with a triggered-phase transient analyzer to make sure that the phase disturbance due to the interferometric RF switch is negligible.[108]The spurs of the interrogation microwaves will also introduce a frequency shift especially when the spur frequency components are within the Rabi transition envelope. Thus,the spectrum of the interrogation microwaves needs to be checked to make sure the spur amplitudes below-60 dBc and the amplitude difference less than 1 dB,which makes sure the corresponding fractional frequency shift well below 10-16.[109]Even with a high Q Ramsey cavity,there is still weak residual travelling waves inside the cavity which will cause a frequency shift when the atoms cross the cavity at different positions during the ascending and descending. With the theoretical study of microwave cavity phase,[93]the transverse phase can be expressed in a Fourier series cos(mφ) with cylindrical coordinates (ρ,φ,z).Only m ≤2 terms are significant since the cavity apertures restrict the atomic trajectories to small ρ. The m=0 component represents power flowing with symmetries from the cavity midplane to the endcaps. The m=1 component represents power flowing with symmetries from one side of the cavity to the other, and the m=2 component represents a quadrupolar flow from opposing feeds. With each component carefully evaluated, the frequency uncertainty induced by DCP can be lowered down to a few parts in 1016,although it is still a dominate uncertainty source in many fountain clocks.[93,110]

4. Operation of optical clocks

Different from a fountain clock,atoms for optical clocks are trapped in a potential during the interrogations. The general experimental sequences are similar and shown in Fig. 6.First, the reference ensemble is laser cooled to the Lamb-Dicke regime where the probing laser wavelength is much higher than the ions/atoms confinement region,[111–114]and then prepared in a clock state. After a highly stable probe laser is applied to induce a clock transition, the atomic state is detected and used to lock the probe laser frequency to a clock transition. Similar to a fountain clock, an optical clock includes an ultra-stable laser(USL)as the LO,a quantum reference system (ions or neutral atoms), and a locking system.Ion optical clocks usually trap single ions in a radio frequency(RF)trap, while neutral atom optical clocks trap many atoms in an optical lattice.

Fig.6. An optical clock consists of an ultra-stable laser,an atomic reference system, and a locking system. The type A system is an optical clock with neutral atoms trapped in an optical lattice. The type B system is a single ion optical clock.

4.1. Ultra-stable laser

USL is a key ingredient in an optical clock.[114–120]To achieve a low instability, an USL should have extremely narrow linewidth and ultra-low instabilities. Usually, USL is obtained by locking a laser to a high-Q ultra-stable optical cavity with the Pound–Drever–Hall technique.[121–123]Thus, the laser frequency instability is determined by the instability of the optical cavity. To reduce environment fluctuations,[120,124–129]the cavity is supported by highly rigid spacers which are properly placed on calculated positions to lower the deformation of the cavity due to the gravity. The cavity is placed in a temperature stabilized vacuum system as shown in Fig.7 which is usually mounted on a vibration isolation platform and enclosed in a sound insulation box.

When the ambient vibration sources have been well controlled,the instability of the locked laser will be limited by the heating noises from the cavity.[130]Most of the optical cavities are fabricated with ultra-low thermal expansion glass,and operating at its zero expansion temperature to limit drifts of the cavity length. Cryogenic crystal silicon cavity has also been used to lock a laser,and a frequency instability of a small fraction of 1017has been achieved.[131]Meanwhile,the instability can also be improved by increasing the cavity length to reduce the heat noise effects. An instability of 8×10-17at 1 s has been obtained with a 48 cm ULE cavity.[132]

Fig.7. A sketch of a temperature stabilized ultra-stable cavity in a vacuum chamber.

4.2. Ion trapping and cooling

Dehmelt proposed the idea of using trapped ions as the references of optical frequency standards in 1973, and laser cooling technologies speed up its developments.[49,50]Up to now, several kinds of ion optical clocks have been realized, which are40Ca+ion clock,[13,133,135–139]88Sr+ion clock,[140,141]199Hg+ion clock,[142]171Yb+ion clock,[143,144]and Al+ion clock.[56,145–147]For Sr+(Ca+, Hg+, and Yb+)ion clocks,only one ion is trapped. While,due to no 167.1 nm lasers available for Al+ion cooling, an Al+ion needs to be sympathetic cooled by cotrapping a logic ion based on quantum logic spectroscopy.[148]

According to the cooling theory, Paul trap which only uses RF and dc electric fields is more suitable for ion optical clocks than a Penning trap.[149,150]The basic geometry of a Paul trap[149,150]is shown in Fig.8(a).It consists of a cylindrical ring and end cap electrodes. A single ion can be trapped in the center by loading a dc and an ac voltage. For a better optical access,the Paul trap is redesigned,and the center cylindrically symmetric ring is removed as shown in Fig.8(b).[151,152]Both types of Paul traps are suitable for single ion traps. For Al+ion optical clock,a linear Paul trap is more suitable which can trap multiple ions as shown in Fig.8(c).[153,154]

Fig.8. The sketch of Paul traps for ion optical clocks. (a)The cylindrically symmetric electrode geometry used by Paul. (b) The geometry for endcap Paul trap. (c)The geometry for linear Paul trap.

Fig.9. Schematic energy level diagram of clock ions. The blue line,the transition for cooling and detection. The red line,the transitions for repumper. The orange lines,the transitions for clock.

After being trapped, the ions are cooled and prepared in the clock states.[155]The schematic energy level diagrams[57]of different ions are shown in Fig. 9. Due to a deep trap depth,the ions will be cooled down to the Doppler limit in the Lamb-Dicke regime with one cooling beam. Additional cooling could be applied to further reduce micromotion induced frequency uncertainty.

The energy levels of Sr+are simpler due to no hyperfine level splitting, which not only makes cooling easier, but also makes clock transition less sensitive to the external magnetic field. Although Al+has the same advantages,it needs sympathetic cooling by another ion(Be+,Mg+,or Ca+)and makes the system more complicated. For Hg+and Yb+, ground states have hyperfine splittings, a cooling laser is frequency modulated at the frequency of the hyperfine level separations for repumping. The clock transitions are also quadrupole transitions from the2S1/2ground to the D excited state with linewidths of 1.8 Hz and 0.4 Hz, respectively. Repumping lasers to pump ions back to2S1/2are applied for cooling and detection. Besides a quadrupole clock transition, an octupole transition from the ground2S1/2to2F7/2state with the linewidth at 10-9Hz is also a clock transition with more advantages, although another repumper is needed as shown in Fig. 9.[156]Some common physical effects can be cancelled out with this energy structure of two clock transitions within one ion, making it a prospective tool for precision measurements. For an Al+optical clock, the1S0→3P0transition is the clock transition,and the1S0→3P1transition is applied for the quantum logic spectroscopy.

Limited by the quantum projection noise, the short-term instability of a single ion optical clock is on the order of 10-15.[157]To reduce the quantum projection noise,multi-ion optical clocks have been proposed where two or more ions are trapped in a linear Paul trap. However, the motion becomes strongly coupled in this case. Recently, a scalable precision multi-ion trap array has been designed by Pyka et al.[154]With this system,the expected type B uncertainties related to multiion effects can be lower than 1×10-19.

4.3. Laser cooling and trapping of neutral atoms

Different from single ion optical clocks, optical lattice clocks usually have 103–104neutral atoms,thus a much lower instability(～10-16or even lower)at 1 s can be achieved.[158]To date,optical lattice clocks have been realized based on the Sr,[159–169]Yb,[170–176]and Hg atoms.[177]

The preparation of a quantum reference system includes laser cooling,optical lattice loading,and state preparing. Corresponding energy levels for these 3 optical lattice clocks are shown in Fig.10,and the structures are similar.

Fig.10. Schematic energy level diagrams of several neutral atoms.

Due to a short lifetime of the1P1state and the correspording high temperature of the Doppler cooling limit, two cooling steps are usually applied. During the primary cooling stage,[178,179]Yb/Sr atoms are trapped and cooled to a Doppler limit in a blue MOT with1S0→1P1cooling lasers,3P0→3S1and3P2→3S1repump lasers, and an anti-Helmholtz coil. At this stage, the Doppler cooling limit is below 1 mK. After a blue MOT stage,a red MOT(1S0→3P1cooling)is applied to cool down atoms to μK.[180–182]For the Hg atoms, the atoms can be cooled to μK in just one step.

After being cooled, atoms are loaded into an optical lattice.In an optical lattice,atoms have both internal and external energy states.[183]To approach confinement capable of a pure internal state measurement,several important criteria must be met.

First, the atoms are operated in the resolved-sideband regime where the high modulation frequencies of the Doppler effects are far from the carrier transition to reduce the Doppler effects.[184,185]

Second,the atoms are moved into the Lame-Dicke regime where the recoil effect is reduced.[186]Figure 11 is the resolved sideband spectroscopy of Sr atoms in a Lamb-Dicke regime. In addition, the relative areas of red and blue sidebands can be used to obtain atoms’longitudinal temperature.The longitudinal trap frequency of atoms can be estimated from the sharp edge of the blue sideband.

Fig.11. Resolved sideband spectroscopy of strongtium in the optical lattice.Tz (Tr)is the atomic temperature in the longitudinal(radial)direction of the lattice.

Ac-Stark effect due to the optical lattice field will shift a clock transition frequency. As proposed by Katori et al.,it is possible to tailor the trapping field (magic wavelength)so that the Stark shifts of the ground state and the excited stage are the same, and the first order Stark shift of the clock states can be eliminated.[55]The last is to obtain an ultrahigh resolution spectroscopy by optimizing the magnetic field and spin polarization.[187]During the cooling, the magnetic field is compensated,and then a bias magnetic field and a beam of polarized light are applied to pump atoms onto the desired spin state,and a quantum reference system is established.

4.4. State of art technologies for optical clocks

Up to now,dozens of research groups in about ten countries have engaged in optical clock research. The results are shown in Tables 2 and 3.

Table 2. Summary of global optical clock research status.

Table 3. The uncertainty budgets of the different optical clocks in the world(×10-18).

In general, the systematic frequency shifts encountered in optical clocks are similar. The clock frequencies will be shifted by external fields (DC/AC electric fields and magnetic fields), blackbody radiation (BBR), 2ndorder Doppler effect due to atoms/ions motions,collisions(only for multiple atoms/ions),and electrocircuit loops. Different from fountain clock evaluations,gravitational redshift usually is not included in the uncertainty budgets for most optical clocks.

Through Table 3, it shows that the BBR is one of the greatest contributions for all of optical clocks. The BBR shift[54,57]can be expressed[197]as

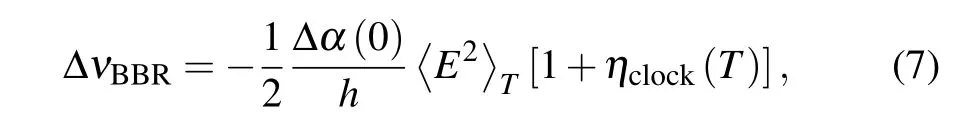
where h is Planck’s constant, Δα(0) is the differential static polarizability between the two clock states,〈E2〉Tis the meansquared electric field inside the blackbody at temperature T,and ηclock(T)provides a small dynamic correction to account for frequency dependence of the state polarizabilities across the BBR spectrum. To precisely measure the BBR shift and reduce the uncertainty, Δα(0) and ηclock(T) should be evaluated exactly first. The experiments to measure Δα(0) are different between neutral atom clocks and ion clocks. For the neutral atom clocks,the approach is to measure frequency shift of a clock transition caused by applying dc electric fields using precision parallel-plate capacitors.[198]For ion optical clocks,one method is based on the observation that the quadratic scalar Stark shift and the time-dilation shift caused by micromotion are correlated and have opposite signs for the clock transition.[74]Another method is to account for the residual spectral dependence of Δα(λ) by performing light shift measurements at various wavelengths.[54]After the Δα(0) is evaluated accurately, the temperature T should be measured exactly, too. At present, the theoretical predictions and/or experimental measurement of the temperature are the limit of low BBR uncertainty. For lower BBR shift, a cryogenic environment,[199]calibrated in situ thermal probes,[200]and a BBR shielding box[198]have been applied in the neutral atom lattice clock.For the trapped ion optical clocks,the static BBR shifts are generally smaller than those of the neutral atom lattice clock at the same temperature due to the tighter binding of the remaining electrons after ionization.

For ion optical clocks, another major frequency uncertainty source is the excess micromotions.[26,54,201]In a real trap,micromotion can be introduced by several effects including the displacement of single ion from the trap center by patch potentials due to charge building up on the trap, a phase difference between ac voltages,and the secular motion of an ion due to its thermal energy. Different methods can be applied to minimize each effect. The displacement can be minimized by applying voltages to trim electrodes. The phase difference can be minimized with a phase shifter. And the secular motion can be reduced by lowering the ion temperature.

For optical lattice clocks,the lattice Stark shift is another major frequency uncertainty source. The lattice shift can be measured by detecting the frequency shift between different lattice intensities. The differential ac Stark shift of the two electronic clock states Δϑacis given[202]by

5. Frequency measurements and comparisons of optical clocks

As the secondary representations of the SI second,an optical clock frequency needs to be measured with a primary frequency standard. Since the development of optical frequency comb(OFC)which connects the optical frequency and the microwave frequency in 2000,the direct measurement of optical frequency becomes much easier. Meanwhile, many applications of an accurate optical frequency also require converting to microwave frequency with an OFC first. Figure 12 shows frequency measurement schematic diagram of the optical laser by using optical frequency comb.

Fig.12. The frequency measurement schematic diagram of the optical laser by using optical frequency comb.

An OFC is composed of a series of equi-spaced singlefrequency modes. The mode space and the first mode are the repetition rate (frep,fr) and carrier envelope offset frequency (fCEO), respectively. The n-th mode frequency (fn)can be expressed as tnfr+ fceo. Here, both frand fceoare in a microwave domain, and link an optical frequency with microwave frequencies. After stabilizing frandfceo, the mode frequencies can be stabilized.[203]Then,by measuring the heterodyne beat frequency(fbeat)between the n-th mode and the laser, the laser frequency can be determined by fL=n fr+fceo±fbeat. The±is determined by whether the n-th frequency mode or the unknown laser is at higher frequency.

To measure an optical clock frequency, the frand fceoshould be locked to a H-maser which is linked to a primary frequency standard or time scale UTC which links to a primary frequency standard ensemble reported to BIPM.[72,204]So far, each optical frequency as the secondary definition of SI second has been reported more than once. Among them,Sr optical transition with the highest measurement uncertainty of 0.11 Hz[205]has been measured 16 times.

Due to its high performance, comparisons between optical frequency standards directly are necessary to provide consistency checks of the performance and accuracy of the various clocks. When both optical clocks are of the same type,the two optical frequencies can beat frequency directly.So far,the frequency difference between the same type optical clocks can reach 10-19order of magnitude.[79]For two types optical clocks, the optical frequency should be converted by an OFC.In addition,the uncertainty imported the equipment and links should be considered and non-negligible. So far, several kinds of frequency ratios between two types of optical clocks[198,206–209]have been measured which can reach 10-17order of magnitude.

6. Future redefinition of the second

The present definition of the SI second is based on taking the fixed numerical value of the Cs frequency ΔνCs, the unperturbed ground-state hyperfine transition frequency of the133Cs atom,to be 9192 631 770 when expressed in units of Hz,which is equal to s-1.[210,211]The Cs fountain clocks are the primary frequency standards to realize the definition of the second. Since 2005, the developments of optical frequency standards have been boosted, and the evaluated type B uncertainties of the best optical clocks are 2 orders lower than the best Cs fountain clocks, raising the question of a redefinition of the second based on optical atomic transitions. A roadmap towards a new definition of the second was setup by strategy planning working group of the CCTF (Consultative Committee for Time and Frequency) in 2015.[212]Five milestones were proposed in order to make a redefinition possible.

1. At least three different optical clocks (either in different laboratories,or of different species)have demonstrated validated uncertainties of about two orders of magnitude better than the best Cs atomic clocks at that time.

2.At least three independent measurements of at least one optical clock of milestone 1 were compared in different institutes (e.g., Δν/ν ＜5×10-18) either by transportable clocks,advanced links,or frequency ratio closures.

3. There are three independent measurements of the optical frequency standards listed in milestone 1 with three independent Cs primary clocks,where the measurements are limited essentially by the uncertainty of these Cs fountain clocks(e.g.,Δν/ν ＜5×10-16).

4. Optical clocks (secondary representations of the second)contribute regularly to TAI.

5. Optical frequency ratios between a few (at least 5)other optical frequency standards have been performed; each ratio measured at least twice by independent laboratories and agreement was found(with e.g.,Δν/ν ＜5×10-18).

One option for a redefinition of the SI second is to choose a single atomic transition similarly to what is currently done.However,current optical clocks are being developed with various atomic species and various technologies,and none of these optical transitions stands out as an obvious choice for a new definition. A combination of an ensemble of selected optical clocks would be an alternative way.[213]Lodewyck proposed the second to be defined by taking the fixed numerical value of the weighted geometric mean of the best realized atomic clock transitions to be a constant N when expressed in units of Hz as following:

where νiare the individual transition frequencies, N is a numerical constant,and ωiis the normalized weight of the clock transition νi. The normalization of the weights ensures that it has the dimension of a frequency Hz. The drawback to this idea is that the constant N would have no physical significance. It also would require regular updating,and acquire significantly different values with the introduction of new frequencies. There are also some other proposals to redefine the second, and one is fixing the De Broglie-Compton frequency of the electron by fixing its mass: νe=mec2/h.[214]Here,the speed of light c and the Planck constant h are defined constants with no uncertainty, and the uncertainty of the electron mass is 3.0×10-10, according to the CODATA 2018, much larger than the current uncertainty of the fountain clocks.

7. Applications and future prospects

Besides calibration of the time scales, atomic frequency standards are important in a wide range of different applications from fundamental science[215]to socioeconomic networks,including global satellite positioning systems,telecommunications, energy distribution, legal time stamping, etc. A few examples are discussed in this section.

7.1. Realization of atomic time scales

One of the most important duties of time and frequency community is to generate time scales. International atomic time cooperation under the organization of Time Department of the Bureau International des Poids et Mesures (BIPM) is responsible to produce, maintain, and disseminate the atomic time scale commonly used worldwide. Free atomic time(EAL)is a weighted average based on about 450 commercial time-keeping atomic clocks in about 80 laboratories around the world. Each participating laboratory realizes a timescale UTC(k), which approximates UTC and is used as the local time standard in our daily life. The primary and secondary frequency standards continuously steer EAL to generate International Atomic Time(TAI).TAI unregularly inserted leap second is the Coordinated Universal Time (UTC) commonly applied worldwide. So far, 17 fountain clocks and 5 optical clocks have been evaluated and reported to BIPM to calibrate TAI.Figure 13 shows the relative frequency difference between f(TAI) and f(TT). TT is the terrestrial time, which agrees with the SI second on the rotating geoid (the gravitational equipotential surface closest to mean sea level). BIPM calculated TT(BIPM) is based on a weighted average of the evaluations of the frequency of TAI by the primary and secondary frequency standards. It shows in the figure that the frequency difference between TAI and TT was drops to a few parts in 1015after the fountain clocks were used to calibrate the TAI.

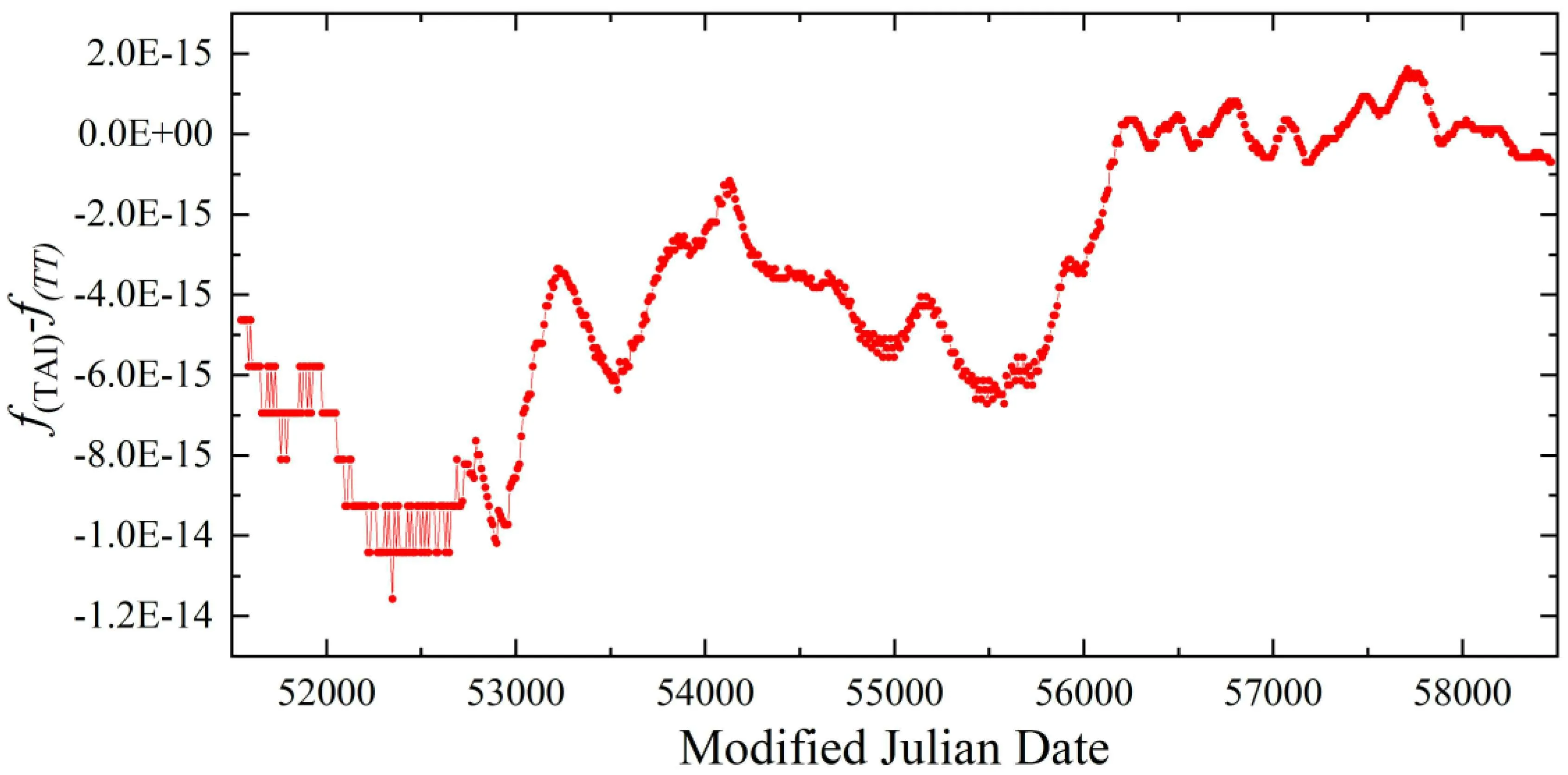
Fig.13.Relative frequency difference between f(TAI)and f(TT)from MJD 51549(Jan. 6th,2000).

In 2017,the relative frequency instability of TAI was estimated to 3 parts in 1016for mean duration of one month.

7.2. Tests of fundamental constant variations

The most precise tests of time variation of fundamental constants were carried out using atomic clocks.[141,216,217]In the standard model, all fundamental constants are invariable with time, while in theories beyond the standard model,the dimensionless constants become dynamical. The frequency ratios of two clocks over time may set limits on variation of fine structure α, the proton-to-electron mass ratio μ(mp/me), and nuclear g factors. At present, the limitation constraints on temporal variations of α and μ from comparisons of atomic transition frequencies are due to combinations of several experiments tracking ratios of different clock transitions.[63,144,196,217]The Al+/Hg+optical clock comparison set the limit: ˙α/α =(-1.6±2.3)×10-17yr-1.[216]The frequency ratio of those two transitions (E2 and E3) in Yb+was measured directly using the same single ion of171Yb by Godun,[144]and combining this measurement with previous experiments set the limits to the variation of α and μ as following:

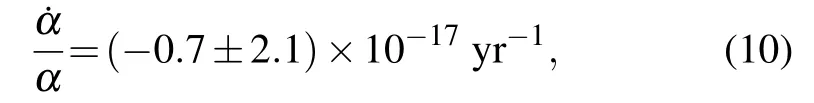
Frequency standards in space with a highly eccentric Earth orbit[218]or a solar system escape trajectory[219]can also be used for searching dynamical variations of fundamental constants,such as Einstein’s theory of relativity,fundamental couplings of the α and μ values to the gravitational potential,detecting a time varying dark matter field or gravitational waves(GW).[220]

7.3. Geodesy

Currently, altitudes are determined through geometric leveling, with typical single-setup distances of around 50 m,which is time trivial and labor consuming. An alternative approach uses accurate global navigation satellite systems(GNSS)data together with gravity field modeling from satellite gravimetry supported by terrestrial gravimetry.[221]The GNSS approach produces disagreement of several tens of centimeter with purely terrestrial measurements.[222,223]A new and independent method “relativistic geodesy” or “chronometric leveling” is proposed which allows long distance altitude difference measurements by comparing the frequencies of remotely located optical clocks.[224,225]According to general relativity, a clock ticks slower in a deeper gravitational potential. This gravitational red-shift is Δφ/c2,to the first order. Here,Δφ is the gravitational potential difference and c is the speed of light. The magnitude of the fractional frequency shift is about 1.1×10-16per meter of altitude near the geoid.With a fractional frequency accuracy of optical clocks down to 10-18–10-19and frequency comparison via optical fibers or free-space microwave[226–229]or optical[230–233]satellite links,it provides a new tool of measuring equivalent height with a resolution of about 1 cm. By combining the gravity potential provided by optical clocks and its derivative(the gravity field)as measured by gravimeters,one can estimate the size and location of a density anomaly,[234]an important application in Earth exploration.

7.4. Navigation

Navigation has become an indispensable part in our daily life. Nowadays, global navigation satellite systems(GNSS) such as US global positioning system (GPS), Russian global navigation satellite system (GLONASS), European GNSS (GALILEO), China’s BEIDOU navigation satellite system[235–238]are more and more used by different users to determine their locations. In these systems, the position is determined by measuring the travel time of the microwave signals broadcast from satellites,which is proportional to the distance between the location and each satellite of the constellation. Thus,accurate and ultra-stable atomic clocks,which are carried on each satellite for time scale signal generations,play a critical role because a distance is calculated from the time difference,any error in the measured time leads to an error in the calculated position. 1 m navigation precision requires that the time scale on all the satellites to be synchronized within 3 ns.

8. Conclusion

Cold atom has been crucially important in precision measurements. In this paper, we focus on its applications in frequency standards. Since the definition of the SI unit‘second’changed from astronomical observations to atomic transition,atomic clocks made remarkable progress, especially after the developments of the laser cooling and trapping atom techniques. Significant improvements have been made in clock’s instability,reproducibility,and accuracy. Primary Cs fountain frequency standards have gained orders of magnitude in accuracy compared with Cs beam clocks, and achieved a total uncertainty only a few parts in 1016. Trapped ion and neutral atom optical frequency standards have exceeded the best Cs fountain clocks, and reaching an uncertainty in a range of 10-18–10-19. These developments have led to the recommendations of secondary representations of the second and a future redefinition of the second can be anticipated. However, there also remain the challenges of making high accuracy comparisons between optical clocks located in different countries especially between continents. Besides applications in the metrology,navigation,etc.,ultra-stable and highly accurate atomic clocks are also powerful tools for measuring fundamental constant variations and searching for new physics.