基于GADF与卷积神经网络的滚动轴承故障诊断研究*

刘红军,魏旭阳

(沈阳航空航天大学 机电工程学院,辽宁 沈阳 110000 )

0 引 言

在现今机械设备中,旋转机械是机械设备中最常见和最重要的组成部件之一。滚动轴承作为旋转设备最基本的结构之一,对机械设备的寿命与稳定性有着决定性的影响。

因此,国内外许多学者对滚动轴承的故障检测进行了深入的研究[1],并提出了许多有价值的方法。大部分检测方法多采用对滚动轴承的故障信号进行分析,提取有效特征作为输入,导入各种分类器中进行识别。如杨宇等[2]通过EMD和神经网络结合的故障诊断方法;刘韬等[3]通过KPCA和耦合隐马尔科夫模型的轴承故障诊断。

但此类方法存在过程复杂、缺少灵活性、对专家的经验与知识具有依赖性,以及分类器缺少非线性拟合能力等问题。

近些年来,深度学习的非线性拟合能力在轴承故障检测方面得到了充分的展示,并获得了理论上的高精度诊断水平。其中,卷积神经网络(CNN)因其自身具有共享权值与偏重、局部感受野和子采样测量等特点,与深度信念网络(DBN)[4]和限制玻尔兹曼机(RBM)[5]等其他深度学习方法相比,在语音以及图像分类任务方面具有较大的优势。同时,其在故障诊断领域的应用也日益增多。

CNN在执行数据分类任务时,作为输入的数据集可分为一维数据和二维数据两类。如孙曙光等[6]提出的一维CNN的低压万能式断路器附件故障诊断;肖雄等[7]的一种二维CNN优化轴承故障诊断方法。WU Y等[8]对两种类型数据进行了比较,认为在已有的大多数CNN模型中,二维图像数据更适用于神经网络的模型的训练。而如何将一维振动信号清晰地转化为二维图像数据,成为智能故障检测的重要难点。

基于以上分析,笔者提出一种新的故障诊断方式,由格拉姆角差场(GADF)时间序列编码方式[9]将一维时序数据转换为二维图像数据,并结合改进的CNN模型进行预测,以达到高精度诊断的效果。

1 格拉姆角差场图像编码转换

GADF图像编码的本质是通过格拉姆角场(GAF),将获取到的一维时序数据转化为二维图像数据的方法;将时间序列X缩放入区间[-1,1],再将其极坐标化得到x。

其过程如下:

(1)

θ=arc cos(xi),-1≤xi≤1,xi∈X
r=ti/N,ti∈N

(2)

经过上述变换过程,即可将一维时间序列数据转换为对称的带有颜色、点、线的对称特征图像。

当GAF基于正弦函数时生成格拉姆角差场(GADF),如下式所示:

(3)

通过编码转化为二维图像,GADF编码的示意图如图1所示。

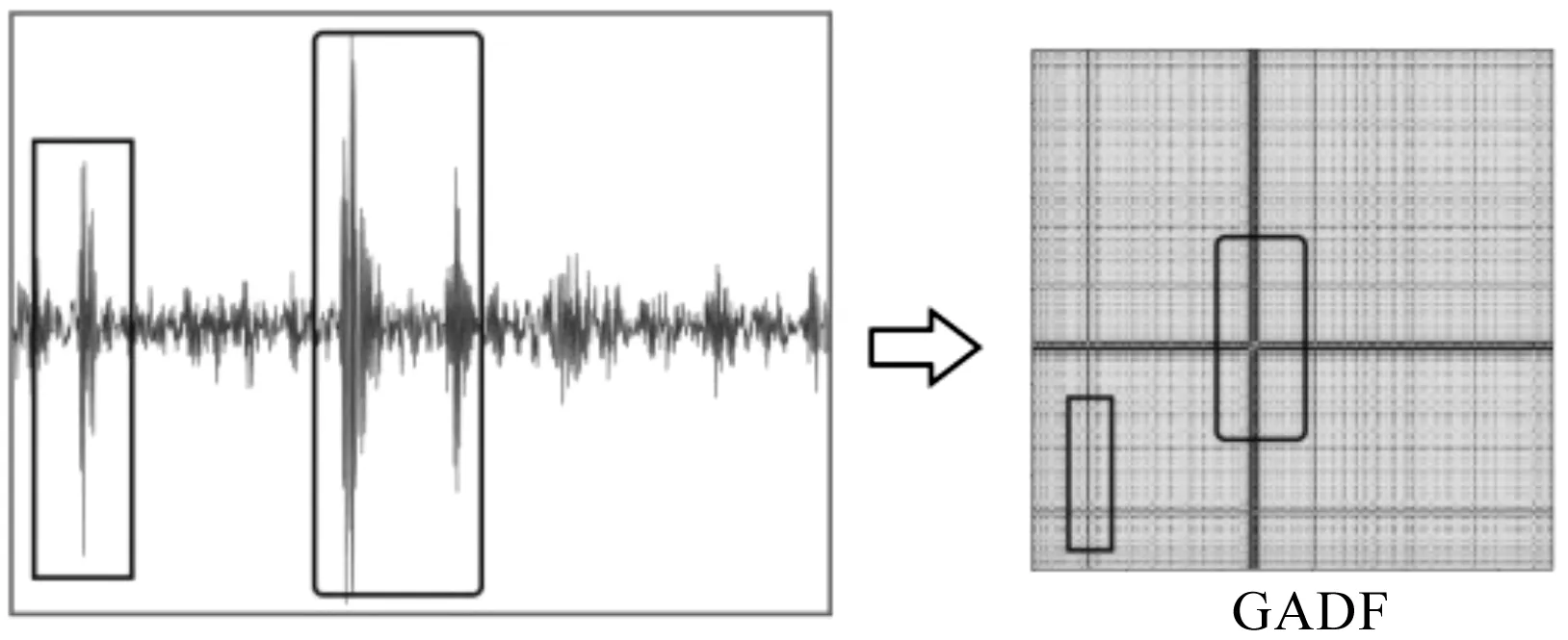
图1 GADF编码示意图

在图1中，当第一个波峰出现时,在两种特征图中出现颜色较浅的对称交叉线;而当峰值波动较大时,特征图中与其对应的对应交叉线其颜色更为明显;

与此同时,其余较小的震动在GADF特征图中也完整地表现出来。

由此可见,GADF可以将滚动轴承的震动信号完整地映射为二维特征图像,并作为CNN模型的输出。

2 卷积神经网络

卷积神经网络(CNN)是一种前馈式神经网络,其卷积层与池化层具有强大的数据特征提取能力,适用于处理图像与声音等网状结构数据,神经网络模型中滤波器通过对输入数据的迭代和分析来获得更多的有效特征和隐藏信息;同时结合稀疏式全连接和权重偏置的共享机制,在时间与空间上进行采样,降低了数据的复杂程度,相比其他神经网络结构类型减少了训练量,有效避免了算法过拟合。

CNN模型结构简图如图2所示。

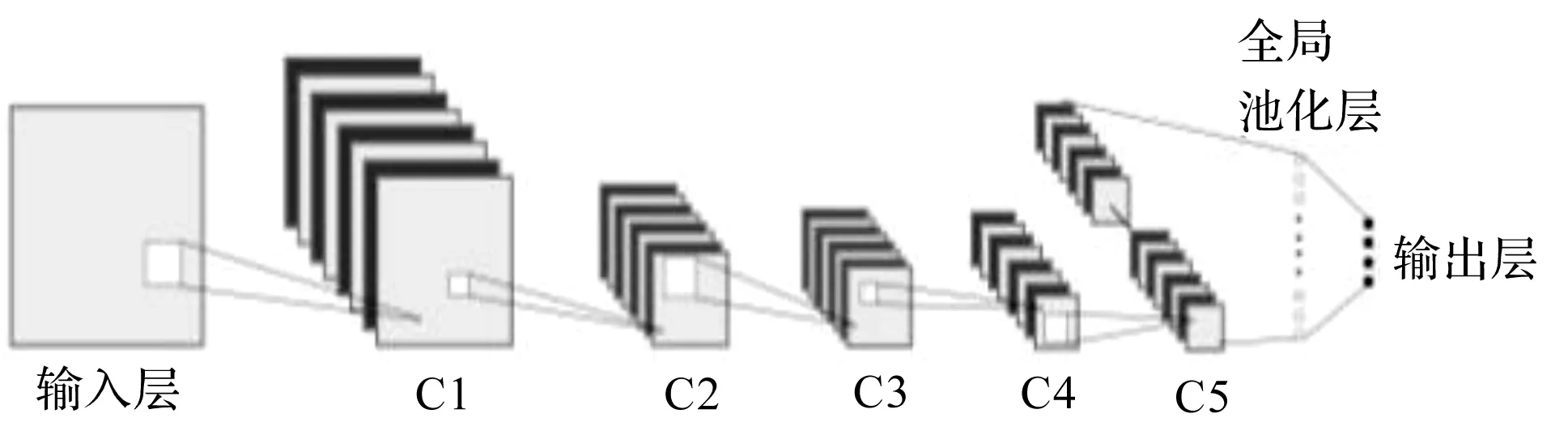
图2 CNN模型结构简图

2.1 卷积层

卷积层是整个神经网络模型的核心所在,它通过对输入图像数据的卷积运算提取图像中的特征信息。

卷积层的具体运算如下:

(4)

2.2 池化层

池化层的主要目的是降低卷积层处理后的数据维度。因为卷积后的数据虽然具有了之前数据的特征信息,但是其特征维度也急剧增长。为了汇总特征平面的输出,通常采用两种池化方式,即平均池化与最大池化方式。

其中,池化层的具体运算如下:

(5)

2.3 全局池化层

与传统的全连接层相比,全局池化层降低了运算的参数量,提高了模型的泛化能力,减少了过拟合情况的发生。与Dropout[10]相比,全局池化层提高了正则化效果。

在现代卷积架构中,全局池化已经逐渐取代了Dropout的位置。全局池化[11]的核心思想是,将每张图片的所有特征值融合为一个特征值,实现张量的降维转换,使特征值的维数等于最后一层卷积层的数目。

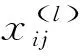
(6)

(7)

其中,式(6)代表的是最大全局池化,式(7)为全局平均池化。

3 试验研究

3.1 数据采集及编码

为评估GADF-CNN算法对滚动轴承故障智能诊断的有效性和准确性,此次采用的试验数据集为美国凯西储大学(case western reserve university,CWRU)公开的深沟球轴承故障数据集。

电机负载状态为1 797 r/min、1 772 r/min、1 750 r/min、1 797 r/min 4种,故障分为外圈、内圈与流动体;

采集频率为12 kHz,采用传感器置于电机的驱动端的12个位置进行采集,采集时长为10 s;

因传感器采集信号时,转轴每圈所采集到的采样点约为400个;

为确保数据集的稳定性,每种故障分类样本长度设置为500个采样点,各200个样本。

本文选取1 797 r/min负载下,包括正常状态与11种故障状态的共12种情况作为数据集,分别由0～11数字表示,取前80%为训练集,输入已建立好的CNN模型;其余为测试集对训练好的神经网络模型进行检验。

二维故障图分类图如图3所示。

图3 二维故障图分类图

3.2 卷积神经网络模型超参数优选

超参数的选择决定了整个卷积神经网络模型在故障诊断的精准度,通常CNN中主要的超参数有卷积核、池化核、优化器、激活函数、学习率等。

本次实验为了掌握不同超参数对CNN模型图像处理性能的不同影响经过多次调参,确立了一种由3卷积层与双池化层穿插连接,采用全局池化层替代传统卷积层的神经网络模型。该模型搭建平台为tensorflow2.0.0GPU版,编译语言为Python3.7.3,计算机CPU为i7、Windows10。

改进CNN模型结构表如表1所示。

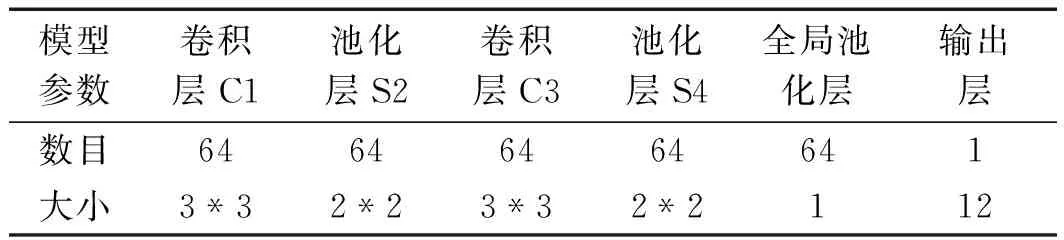
表1 改进CNN模型结构表

3.2.1 激活函数的选择

激活函数决定了CNN模型非线性表达能力,而该激活函数通常根据经验来设置。但是这种方式随机性较大[12]。为此本文选择了常用的3种常用的激活函数进行对比试验。

3种常用的激活函数对比如表2所示。

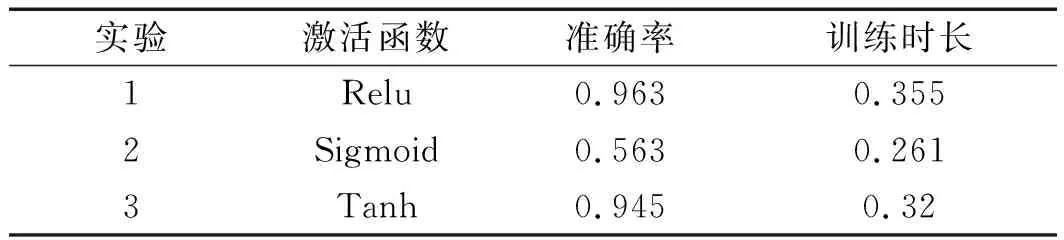
表2 激活函数对比表

由表2可以看出:

实验1准确率最高,虽然在训练用时方面用时最长,但为保证模型的准确度,在改进神经网络模型中,本文选用Relu激活函数。

3.2.2 优化器的选择

在优化器选择实验中继续采用表1中的基准模型参数设置,该实验的卷积层采用Relu激活函数。该实验对目前最常用的SGD,RMSProp和Adam共3种优化器进行测试。

当学习速率为0.000 1和0.001时,Adam与RMSProp的准确率远高于SGD;而当学习速率升高时,RMSProp准确率急剧下降,Adam优化器准确率依然稳定在97%左右。

为此,本文选用Adam小批量迭代优化器。

优化器准确率对比图如图4所示。

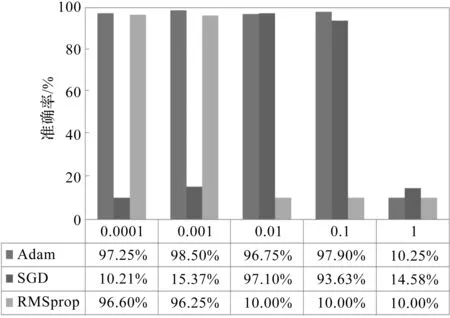
图4 优化器准确率对比图

4 结果分析

4.1 改进的CNN模型评估

为对GADF图像编码下改进的CNN算法的准确性进行有效的评估,本文引用精确率与召回率作为评测指标。其中,精确率是指预测结果中符合该类故障的样本占结果总体的占有率;召唤率是指该类型故障真实样本中被成功预测的样本占类型总体的占有率。

其具体数学表达式如下:

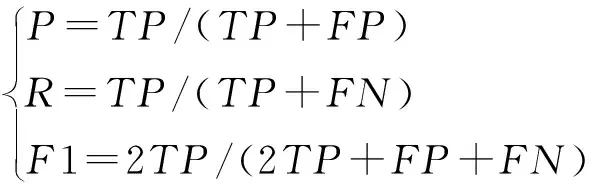
(8)

式中:P—精确率;R—召回率;TP—预测类型与其真实类型相符;FP—预测类型为真,但实际类型为假;FN—实际类型为真,但预测结果为假;F1—精确率与召回率的调和均值。

根据改进的CNN的实验结果,并按公式计算得到的精确率和召回率,如表3所示。

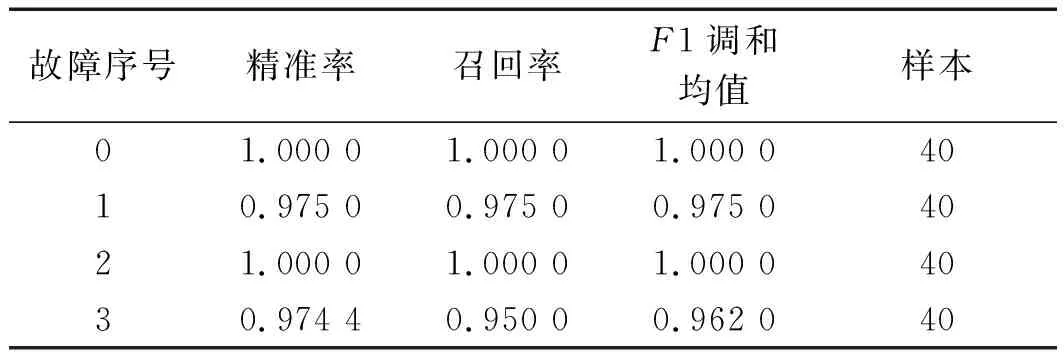
表3 改进CNN模型诊断结果表

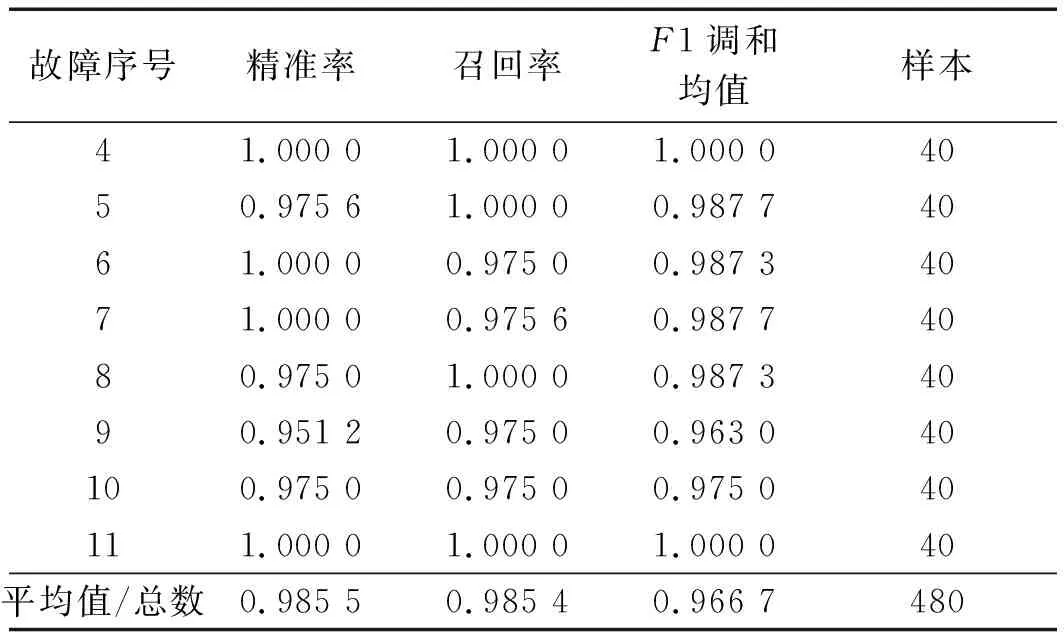
(续表)

为了更深一层地了解改进CNN模型的故障判别情况,笔者引入了多分类混淆矩阵对故障结果进行全面分析;其根据故障的不同等级,样本的真实值与预测值。

故障被误判为何种类型故障等信息如图5所示。

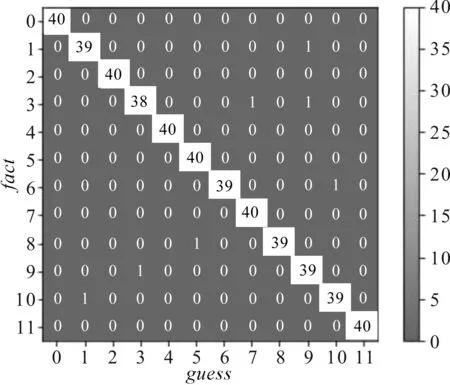
图5 混淆矩阵量化图

由图5可知:在480份测试集样本中,含有7个误测样本,分别为:

将标号1类微小故障判断为标号9类轻型故障;将标号3类轻微故障判断为标号9类轻型故障和7类显著故障;将标号6类轻型故障判断为标号10类轻型故障;将标号8类中度故障判断为标号5类显著故障;将标号9类轻型故障判定为标号3类轻微故障;将标号10类轻型故障判定为标号1类微小故障。

通过分析以上故障类型可以发现,故障误诊类型多为轻型故障,误诊为中大型故障或同级故障类别发生错判,具有一定的预警作用,改进后的CNN模型在正常0、故障2、4和11的情况下诊断准确率为100%,说明这类故障特征较为明显,对旋转设备的危害最大。

经过试验验证可知,该算法综合故障识别率达98.55%,对滚动轴承中的GADF编码图像具有精准的识别能力和优越的诊断能力。

4.2 对比分析

为验证笔者提出的诊断方法的先进性与优越性,此处将GADF-CNN算法与其余3种主流的智能故障诊断算法进行比较。

3种主流智能故障诊断算法分别为BPNN、SAE和SVM[13-15]智能算法。

笔者将二维图像数据测试集按0～11故障诊断序号共12种情况,输入进其余智能算法模型进行训练。

智能算法的对比图如图6所示。

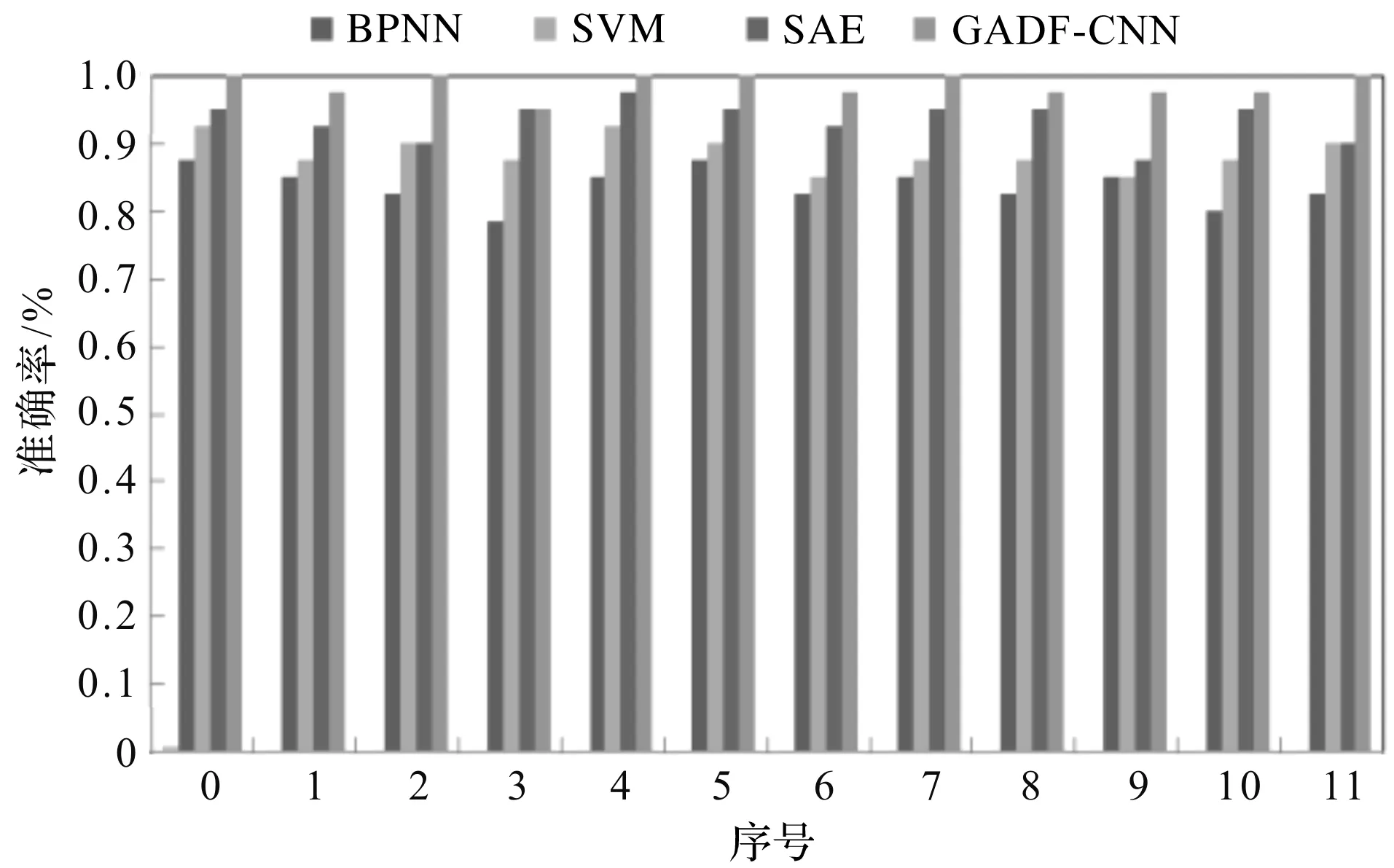
图6 智能算法对比图

由图6可以看出:

BP神经网络模型(BPNN)与支持向量机(SVM)的准确率一直维持在90%以下,准确率较低;而堆栈自动编码器(SAE)的准确率略低于GADF-CNN。

由此可见,改进的CNN模型更适用与对GADF编码图像数据的处理。

详细的准确率如表4所示。

表4 详细的准确率

5 结束语

为充分发挥深度学习识别二维图像在滚动轴承故障检测方面的优势,笔者提出了一种新的故障诊断方式,即格拉姆角差场(GADF)结合改进卷积神经网络(CNN)的智能故障诊断模型,并结合改进的CNN模型对滚动轴承故障进行了预测,达到了高精度诊断的效果。

与其他智能诊断算法相比，GADF-CNN具有以下优势:

(1)在对诊断信号的特征提取方面,相比其他算法的一维时序输入或模态分解等方法,采用领先的格拉姆角差场法将诊断信号转化为具有有效特征的二维图像,对诊断信号的特征提取更为全面,同样也更适合CNN(卷积神经网络)的训练与测试;

(2)在卷积神经网络模型的搭建方面,与其他智能算法的诊断相比,由于输入数据转化为真正的二维图像,使得卷积神经网络强大的线性表达能力可以全面地发挥出来,为此改进CNN模型添加了全局池化层、Adam优化器、交叉熵损失函数等先进的超参数,GADF-CNN算法鲁棒性和泛化能力。

本文的算法已经可以在不同电机负载状态下,对来自于电机驱动端的振动信号做出有效诊断。但由于数据库的有限性,本文没有获取数据库以外的滚动轴承数据进行诊断,该算法仍然存在一定的局限性。

获取数据库以外的数据将成为笔者进行下一步实验研究的重点。