基于主成分分析的薄壁结构截面特征形变识别研究*
2021-05-24梁世雷赵仲航
谢 瑶,张 磊,梁世雷,赵仲航
(河海大学 机电工程学院,江苏 常州 213022)
0 引 言
薄壁结构以其较高的质量-刚度比,广泛应用于工程机械的承重结构[1-4]。高跨比较大的薄壁结构在承受外力时容易产生截面变形,直接影响到工程设备的工作性能,传统的Timoshenko梁等理论忽略了截面翘曲和畸变等高阶形变[5-7],难以为薄壁结构提供一组合理有效的截面变形模式,因此研究薄壁结构的截面特征形变识别具有重要的现实意义。
目前,国内外学者对于薄壁结构截面变形模式的研究主要包括两个方面:在传统梁理论基础上考虑特殊行为的变形模式来改善梁模型,和基于广义梁理论通过特征值解耦微分方程来识别变形模式。YOON K等[8]为不同薄壁结构建立了翘曲函数,并在经典变形基础上添加代表翘曲行为的变形模式。CAPDEVIELLE S等[9]推导了任意形状复合材料截面变形中扭转翘曲的公式,考虑翘曲模式对于构件整体行为的影响。王晓峰等[10,11]研究了横向剪切变形以及横向剪力所产生的翘曲对于薄壁梁振动特性的影响。段海军[12]对薄壁曲梁动力学建模时考虑了弯扭耦合和扭转翘曲的影响,建立了开口截面薄壁曲梁非线性自由振动的有限元模型。随着广义梁理论的快速发展,VIEIRA R F等[13]提出了一个解耦梁动力学方程的准则,以导出一组表示高阶形变的变形模式。PERES N等[14]将广义梁理论扩展到自然弯曲的薄壁梁领域,并导出圆轴弯曲构件包括开放和闭合的截面变形模式。BEBIANO R等[15]通过扩展广义梁理论公式,分析了具有不同截面几何形状的薄壁构件的屈曲行为。
以上研究表明,对于薄壁结构的现有研究方法几乎能够处理任意截面变形的力学行为,但建立的高阶模型微分方程的求解计算较为复杂,在保证精度的同时,一种避免无效的截面特征,仅保留能够反映截面变形本质特征的简化方法对于薄壁结构的动力学模型计算更有效。
基于一组截面基本变形模式,本文建立薄壁结构的一维高阶模型,利用模式识别对一维高阶模型的特征向量分解处理,构建最终权重矩阵,将高阶模型计算出的固有频率和振型与ANSYS模型分析结果比较,以验证模型的可靠性。
1 模型的建立
1.1 位移场一维化
本文以一端固定的矩形薄壁梁为研究对象,结构如图1所示。
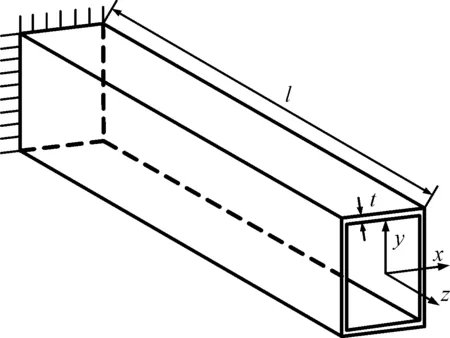
图1 矩形薄壁梁结构简图
图1中,以截面中心为原点,建立空间坐标系(x,y,z),梁体长度为l,壁板厚度为t。
在薄壁梁截面中线上建立局部坐标系,如图2所示。
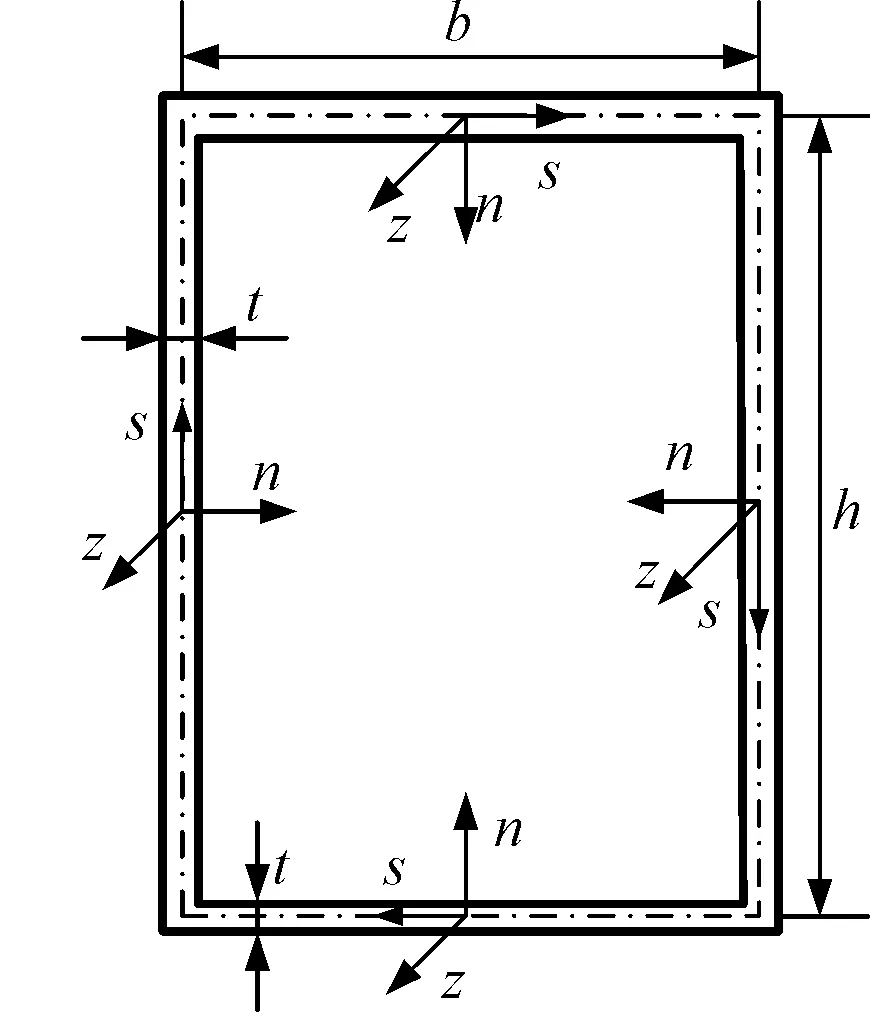
图2 截面中线上的局部坐标系
图2中,沿截面中线建立的局部坐标系由切向s、法向n和轴向z定义,梁体截面中面宽度和高度分别为b和h。
本节借鉴张磊[16]对于薄壁梁的分析方法,在截面上引入8个节点来捕捉截面变形,如图3所示。
图3中,4个角节点为一级节点,4个边线中点为二级节点,分别施加轴向、切向、法向和扭转单位位移,在一级节点上施加位移时,其余一级节点位移为0,在二级节点上施加位移时,其余所有节点位移均为0。本文采用线性函数插值轴向和切向位移,采用埃尔米特插值法向位移,并通过形函数定义基函数,每个基函数都表示一种变形模式,由于模型考虑了4个自由度,共产生32种变形模式,其中1~8为平面外变形,9~32为平面内变形。
截面中线上点的位移通过轴向u(s,z)、切向v(s,z)和法向w(s,z)3个位移分量表示,并通过模态叠加法将截面变形模式的形函数线性叠加,建立截面的一维位移场如下:
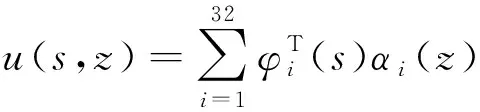
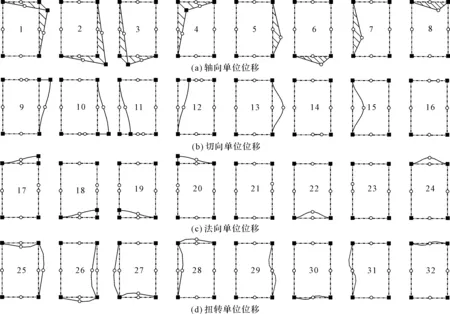
图3 8节点矩形薄壁梁的基本变形模式
(1)
式中:α—幅值函数;φ(s)—平面外变形的基函数;φ(s),ω(s)—平面内变形的基函数。
幅值函数α表示如下:
α=[α1z)α2(z) …α32(z)]T
(2)
三维位移场B(u,v,w)可以表示为:
B=Lψα
(3)
式中:L—微分算子;ψ—位移转换矩阵。
L,ψ分别表示如下:
(4)
(5)
1.2 动力学方程
在小位移条件下,依据Kirchhoff假设,可得薄壁梁的应变分量为:
ε=CB
(6)
式中:C—微分算子。
C的表达式如下:
(7)
根据线弹性本构关系,薄壁梁的应力分量为
σ=Ehε
(8)
式中:Eh—本构矩阵。
Eh表示如下:
(9)
式中:E—弹性模量;v—泊松比;G—剪切模量。
依据Hamilton原理建立薄壁梁的动力学方程,有:
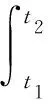
(10)
式中:T—臂架的动能;U—臂架势能;W—外力势能。
T,U,W可以分别表示为:
(11)
(12)
(13)
式中:ρ—薄壁梁材料密度;p—作用在臂架截面上的分布力列向量。
p可表示为:
(14)
将式(11~13)代入式(10),可得薄壁梁的动力学方程如下:
(15)
1.3 有限元格式
本文采用有限单元法求解一维高阶模型,通过拉格朗日线性插值函数将薄壁梁离散为n个单元,即:
α=Ndi,i=1,2…n
(16)
式中:i—单元节点号;N—线性插值函数;d—节点位移向量。
线性插值函数N表示如下:
(17)
(18)
式中:ξ1,ξ2—插值函数;(i),(i+1)—单元两端。
总体节点位移向量D可以表示为:
(19)
将式(16~18)代入式(10),可得:
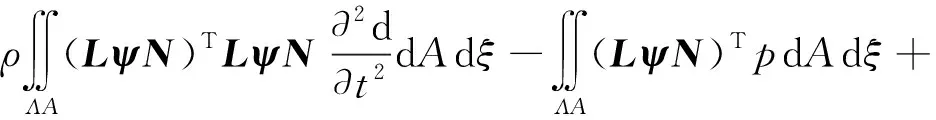
(20)
式中:Λ—轴向积分区域;A—截面积分区域;p—作用在臂架截面上的分布力列向量。
动力学方程的形式可整理为:
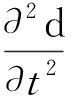
(21)
式中:m—单元质量矩阵;k—单元刚度矩阵;f—单元载荷矩阵。
m,k可以分别表示为:
(22)
(23)
(24)
式中:l—单元长度。
本文研究的薄壁梁处于无阻尼下的自由振动状态,故载荷向量f作为0处理。
求解单元质量矩阵m和刚度矩阵k。组装集成薄壁梁的总体质量矩阵M和刚度矩阵K可以表示为:
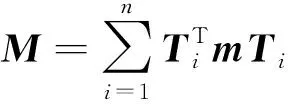
(25)
式中:Ti—节点位移向量di到总体节点位移向量D的转换矩阵。
2 截面特征识别
本文以截面32种变形模式为基础构建矩形薄壁梁的动力学模型,理论上能够完成模型的求解,但是由于考虑的变形模式过多,计算复杂,所以有必要从上述变形中识别出一组合理有效的变形模式来改善模型。
2.1 振型参数提取
高阶模型的特征向量通常被作为识别变形模式的基础,求解薄壁梁高阶模型的广义特征值即可转化得到系统的固有频率,进而求得薄壁梁高阶模型的特征向量,并将特征向量集成在矩阵H中,表示如下:
(26)
式中:(k)—特征向量的阶数。
将每一阶特征向量改写特征矩阵α(k),表示如下:
(27)
由于薄壁梁在轴线方向被离散为n个单元,则α(k)的列向量可以用幅值函数表示为:
(28)
特征矩阵的列向量反映了幅值函数的变化情况,通过对特征矩阵的分解处理以完成截面特征的识别。
对平面内外变形模式的识别是分开进行的,即对原有平面外变形模式识别出新平面外变形模式,对原有平面内变形模式识别出新平面内变形模式,即:
(29)
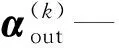
2.2 特征识别算法
主成分分析是通过线性变换将原有多个变量转换为几个线性无关变量的方法。本文利用在投影方向上的方差大小来判断该方向的参与程度。
在特征识别前需要对样本特征矩阵进行去中心化,可得:
(30)
式中:m—特征矩阵中列向量元素个数。
对特征矩阵x(k)构建协方差矩阵A,表示为:
A=x(k)(x(k))T
(31)
对协方差矩阵进行特征分解,求解特征值及对应的特征向量。将最大特征值对应的特征称为主要变形模式,其余特征值对应的特征则为次要变形模式。
将特征值λ由大到小排序,即:
(32)
式中:r—协方差矩阵的秩。
每一阶特征矩阵分解产生的有效变形模式数量取决于q,q为满足下式的最小整数,即:
(33)
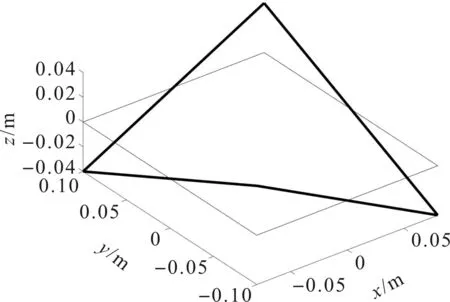
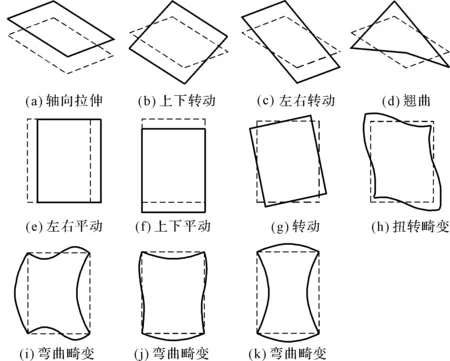
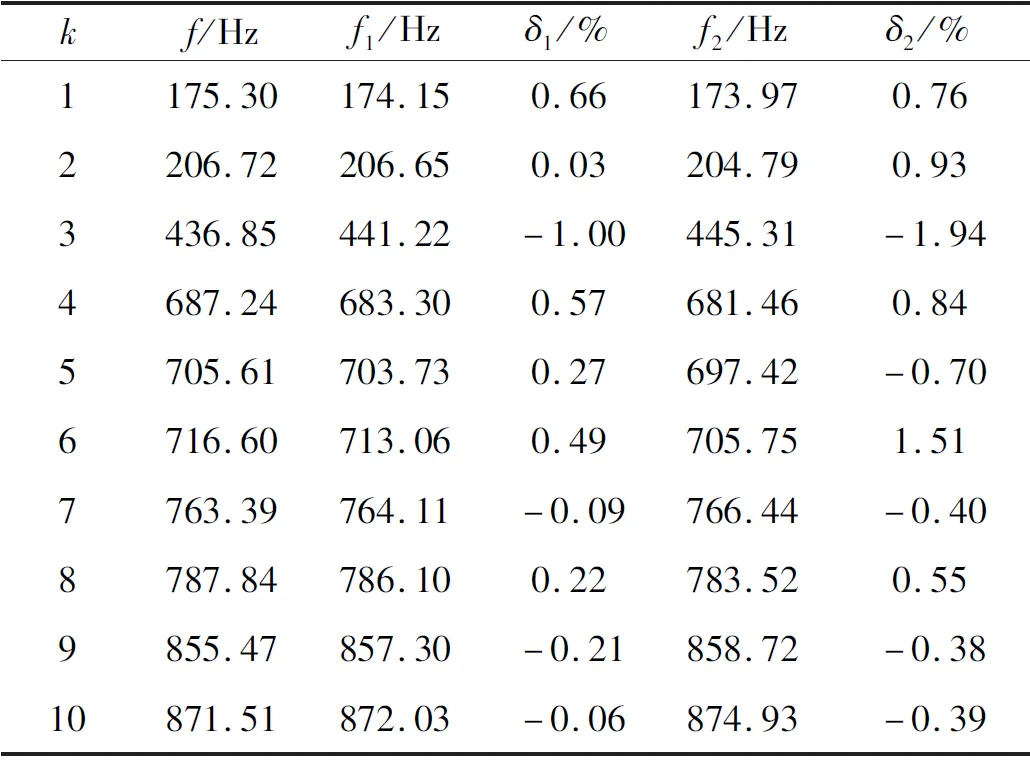
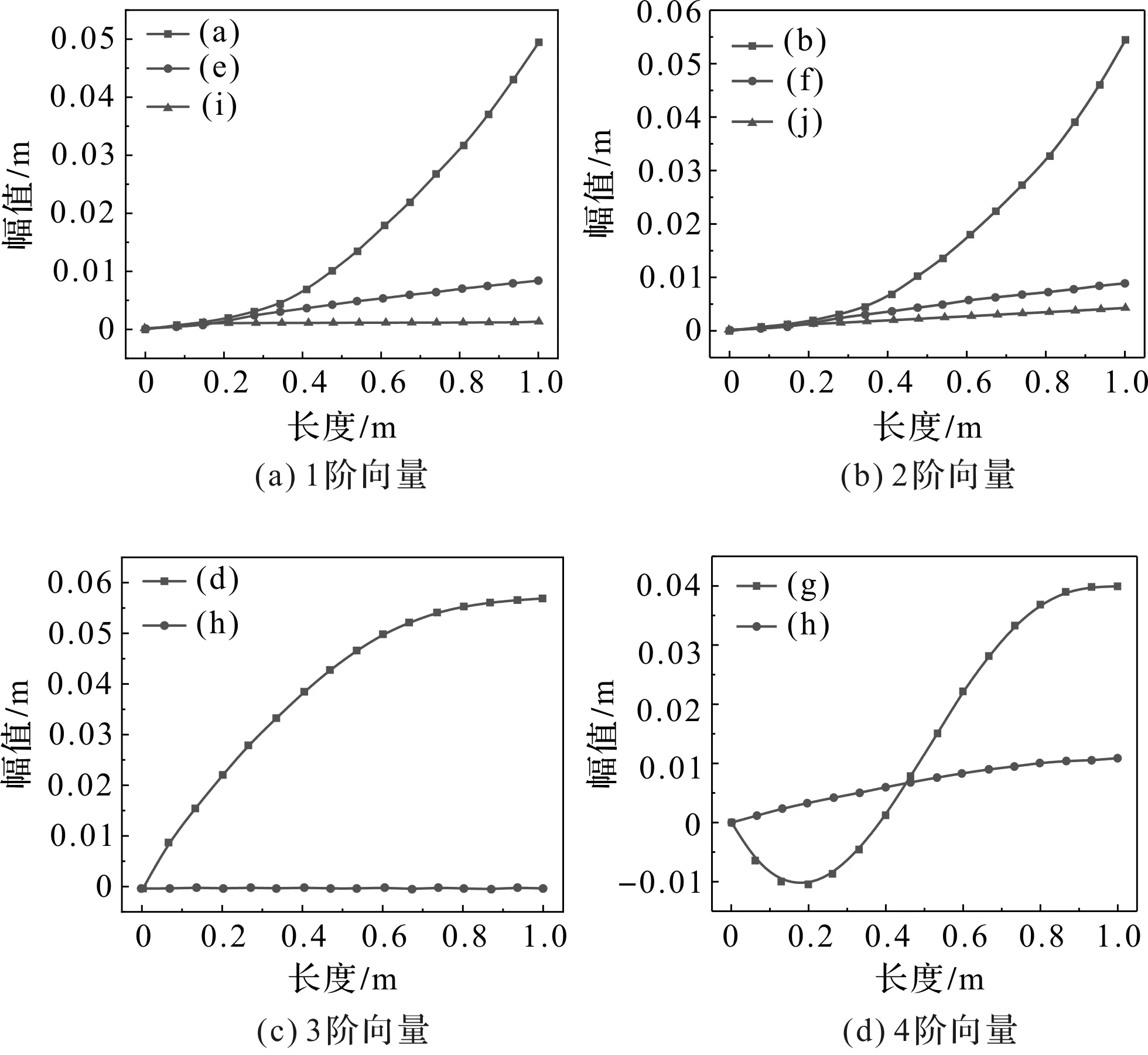
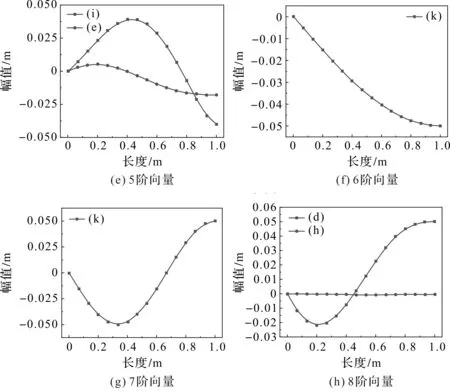
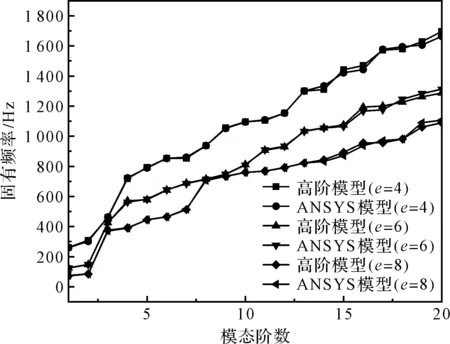
式中:t—阈值,0 (34) 将所有权重系数集成到权重矩阵τ(k)中,即: (35) 在特征识别过程中,某些变形模式可能在不同模态阶数中重复出现,为保证正交性,权重矩阵中的列向量需要满足线性无关性,即: rank(τ(k))=q (36) 最终权重矩阵为截面32种变形模式的线性组合提供了权重集合,表示如下: (37) 式中:ui(s)—轴向位移分量;vi(s)—切向位移分量;wi(s)—法向位移分量。 结合式(21~25),利用MATLAB编制有限元程序,求解薄壁梁的质量矩阵和刚度矩阵,求得模型的广义特征值,分别对平面外和平面内的特征向量分解处理,直至识别出的变形模式满足计算精度的需求;对变形模式的形函数幅值进行归一化处理,以确保其最大位移为1;求解变形模式的形函数,将其用于替换被集成在动力学方程中的基函数,以简化梁模型。 由于从高阶模型的前4阶特征向量中识别出的特征以经典变形为主,本文以矩形薄壁梁第5阶特征向量的平面外变形为例说明了识别过程,识别出具有代表性的翘曲变形,并对识别方法的可靠性和通用性进行验证。 矩形薄壁梁的结构如图1所示,其参数包括:长度l=1.00 m,宽度b=0.16 m,高度h=0.20 m,厚度t=0.01 m,密度ρ=7 800 kg/m3,弹性模量E=2×1011Pa,泊松比v=0.3。 将薄壁梁沿轴线方向离散为n=80个单元,对平面外变形模式的5阶特征矩阵分解处理,协方差矩阵A的特征值为: (38) (39) 结合式(37),可获得一种确定的平面外变形模式,对应于翘曲变形,如图4所示。 图4 五阶特征向量的平面外主变形模式 结合式(30~37),依据特征识别算法流程编制相应的MATLAB计算程序,依次对矩形薄壁梁的前12阶特征向量进行分解处理,共可识别出11种最终截面变形模式,如图5所示。 图5 矩形薄壁梁前12阶振型识别截面变形模式 其中,图5(a~d)为平面外变形模式,图5(e~k)为平面内变形模式;变形模式图5(a~c)和图5(e~g)对应于截面的刚性位移,剩余6种是基于翘曲和畸变的高阶形变,表明识别出的变形模式具有实际的物理意义。 变形模式的排列顺序反映了它们的层次性。其中,图5(a~h)为主要变形模式,图5(i~k)为次要变形模式。 矩形薄壁梁的截面变形模式并不仅仅局限于上述11种变形模式,当需要进一步提高模型的计算精度时,可通过增大阈值t,引入一些参与度较低的变形模式来实现。 本文分别以截面32种和11种变形模式构造薄壁梁的高阶模型1和2。高阶模型均将薄壁梁沿轴线方向均离散为80个单元;ANSYS模型采用Shell 181单元,控制单元尺寸为10 mm,将模型离散为7 200个Shell 181单元,沿梁体轴向100个单元,截面离散为72个单元。 相对误差是以ANSYS模型结果准确的前提下得出的。ANSYS模型固有频率用f表示,两种高阶模型则依次用f1和f2表示,对应的误差用δ1和δ2表示,k表示模态阶数。 薄壁梁前10阶固有频率的比较如表1所示。 表1 前10阶固有频率的比较 由表1数据可得:对比高阶模型1和2,随着考虑变形模式数量的减少,相对误差有所增加,高阶模型1代表了该种模型的精度上限;对比高阶模型2与ANSYS模型,高阶模型2在减少截面变形模式个数后,与ANSYS模型的误差在1.94%以内,模型精度仍能满足计算需求,在保证计算精度的同时提高了计算效率,验证了本文识别方法的可靠性。 高阶模型2的前8阶特征向量的平面外变形模式幅值沿轴向变化如图6所示。 图6 平面外变形模式幅值沿梁体轴向变化 图(6)中:主要变形模式(a~h)的幅值是次要变形模式(i~k)的数十倍,幅值大小体现了它们对于截面变形参与程度的不同。 当模型的计算精度要求不高时,可以选用较高优先级的主要变形模式,以形成更为简化的高阶模型,能够有效提高计算效率。 为了验证所识别出的变形模式的通用性,本文以11种变形模式为基础,对不同长细比e(仅改变薄壁梁长度)下的矩形薄壁梁进行计算分析,如图7所示。 图7中,在长细比e为4、6和8下,高阶模型的计算结果与ANSYS模型吻合良好,表明识别出的变形模式适用于不同长细比的矩形薄壁梁。 薄壁梁前8阶振型比较如图8所示。 图7 不同长细比e下固有频率对比 图8 ANSYS模型与本文模型前8阶振型的比较 图8中,每一阶振型中左侧是在ANSYS shell 181单元下的结果,右侧是基于11种变形模式的高阶模型的振型,右侧网格在横截面上定义为80个点,轴向定义为40个点,采用80×40的矩形来描述薄壁结构振型。 两种振型非常接近,识别出的截面变形模式在振型中都有所体现,这加强了变形模式和振型之间的联系,表明识别出的变形模式和高阶梁模型能够准确再现薄壁结构的三维振型。 针对薄壁结构一维高阶模型求解复杂、效率低等问题,笔者以32种截面变形模式为基础构建了基函数,结合哈密顿原理构造了薄壁梁的一维高阶模型,对薄壁梁的截面形变进行了特征识别,并以识别产生的变形模式重构了高阶模型,分别通过MATLAB和ANSYS进行了数值仿真分析。 研究结论如下: (1)提出了一种薄壁结构截面特征形变识别方法,基于主成分分析对薄壁梁高阶模型的前12阶特征向量分解处理,共识别出11种变形模式;识别出的变形模式具有实际的物理意义及层次性,高阶模型导出的三维振型与ANSYS模型吻合良好,识别出的截面变形模式在振型中都有所体现; (2)以11种变形模式重构了高阶模型,将模型的前10阶固有频率与识别前模型及ANSYS模型结果进行了比较,误差在1.94%以内,在保证精度的同时提高了模型的计算效率; (3)本文所识别出的变形模式具有通用性,适用于不同长细比下的矩形薄壁梁结构。 该研究结果可为提高薄壁结构一维高阶模型的计算效率提供一定的理论依据。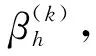
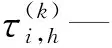
3 数值算例及模型验证
3.1 数值算例
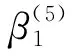
3.2 模型验证

4 结束语
