基于EDEM-FLUENT 耦合的离心选矿机仿真优化分析

和建荣，王进明，俞霞，许振邦

（1.陕西火石咀煤矿有限责任公司，陕西 咸阳 713500；2.中国地质大学(武汉) 地质过程与矿产资源国家重点实验室，湖北 武汉 430074）

立式离心选矿机通过对矿物施加不同的离心力使目标矿物进行有目的性的分离，是矿山机械中主要的工作设备[1-2]。考虑到全球经济对矿石原料的依赖以及世界范围内能源的日益紧缺，针对立式离心选矿机的研究，对于实现立式离心选矿机的节能降耗和高效稳定具有重要意义[3-4]。

为了有效提高立式离心选矿机的分选效率，传统的理论设计与实验周期较长，成本高，难以高效的对立式离心选矿机工艺参数进行优化[5]。近年来，计算机流体动力学与离散元法应用于颗粒分选机理的研究日益增多。王国仪等采用N-S紊流模型研究离心选矿机内流场分布[6]。孙启潇等利用高速摄像机对离心选矿机内部流场运动状态进行研究，获得了流场流速、流体介质运动状态等信息[7]。王旭利用Fluent 软件模拟了立式离心选矿机的流场特性，得到了选矿机内流场分布信息[8]。尽管学者们对离心选矿机进行了大量研究，但得到的流场信息难以准确反映复杂流场的特性。

本文以离心选矿机为研究载体，通过建立离心选矿机三维模型及构建动量交换源项为流固耦合中的传递介质。采用DEM-CFD 耦合法，以反冲水压、转动频率和给矿流量为实验因素，回收率为分选性能评价指标，进行二次回归正交旋转组合数值模拟实验，旨在获得离心选矿机最优工艺参数组合。通过实际分选实验与仿真分选实验的对比，验证DEM-CFD 耦合模型的正确性，为离心分选机构的设计及工艺参数的优化提供参考和依据。

1 离心分选动力学模型的建立

1.1 立式离心选矿机的分选过程及原理

立式离心选矿机在分选锥中的离心分选过程为：当矿浆从给矿口进入分选槽后，矿物颗粒在离心作用下不断向上作螺旋上升运动，同时矿物颗粒将在向壁面运动的过程中不断受到反冲水冲击作用，矿物颗粒由于比重不同将分为轻、重两种颗粒。轻、重颗粒将在反冲水冲击力以及离心力的作用下进行分离。分选中轻颗粒由于无法承受反冲水的冲击力，最终将从离心选矿机的溢流口流出设备成为尾矿，达到富集目标矿物的目的。

1.2 EDEM 中接触模型的建立

在离散元法的分析计算中，软球模型将离散颗粒间的接触类比于阻尼运动，可以较好地描述颗粒间的相互作用。因此，本研究以软球模型为基础进行分析。软球模型的基本原理见图1，其中不同颜色的软球代表不同的粘结颗粒。

图1 软球模型Fig. 1 Soft ball model

基于软球模型的颗粒运动方程为：

式中x 是偏移平衡位置的位移，mm；t 是颗粒运动的时间，s；m 是颗粒质量，kg；η 是弹簧阻尼系数；k 是弹性系数。软球模型的计算基于Hertz 接触理论[9]。Hertz 接触理论其法向重叠量α理论公式为：

式中，R1，R2 分别为两颗粒半径，mm；r1，r2 分别为两颗粒球心位置，mm。

法向接触力Fn 计算公式为：

式中Eeq为等效杨氏模量；δn为法向重叠量，mm；Req为等效接触半径，mm，其计算公式分别为：

式中Ei，Ej分别为两接触颗粒的杨氏模量,MPa；ui，uj分别为两接触颗粒的泊松比，Ri，Rj分别为两颗粒半径，mm。根据Raji[10]理论，法向和切向阻尼力计算公式为：

式中Sn，St分别为法向和切向的刚度，N/m；vnrel，vnrel分别为法向和切向速度，m/s；ξ 为阻尼系数，meq为等效质量，kg。颗粒间力的传递计算通过上述数学模型计算得出，以此保证外部载荷能够实时地反映在Fluent 中。

1.3 固液耦合的数学模型与实现

为了使CFD-DEM 耦合模型能够模拟固液两相流动，采用欧拉-拉格朗日方法将颗粒相处理为离散相，即

由上式可知，流固耦合控制方程中的动量交换源项为

式中，fd为颗粒所受的曳力，Vc为网格颗粒体积，N 为网格中所含颗粒数。

耦合求解的步骤主要为：1.划分模型网格并定义初始流场、颗粒位置、时间步长。2.在一个时间步长后将EDEM 求解器得到的颗粒速度、位置等信息传递给Fluent 求解器。3.通过Fluent 求解器对颗粒的速度等信息进行求解并通过API 耦合接口实时传递给EDEM 中。其中，颗粒与流体交换信息通过固液耦合中的动量交换源相为依据进行传递，其耦合模型流程见图2。

图2 DEM-CFD 耦合模型流程Fig. 2 Flow chart of DEM-CFD coupling model

2 离心选矿机仿真优化与分析

2.1 仿真模型的建立

离心选矿机的主要工作部件是分选锥，应用三维软件Pro/E 对分选锥进行建模，每层分选槽壁面都开有1 mm 的反冲水孔。为了使仿真尽可能高效准确，利用ANSYS Workbench 对分选锥模型进行布尔运算得到其流体域模型见图3。

图3 流体域三维模型Fig. 3 3D model of fluid domain

利用Meshing 对分选锥流体域模型进行六面体网格划分见图4。

图4 分选锥网格Fig. 4 Separation cone grid

采用Hertz-Mindlin无滑动作为分选过程的接触模型，结合文献[11]得到固液两相流仿真参数见表1。

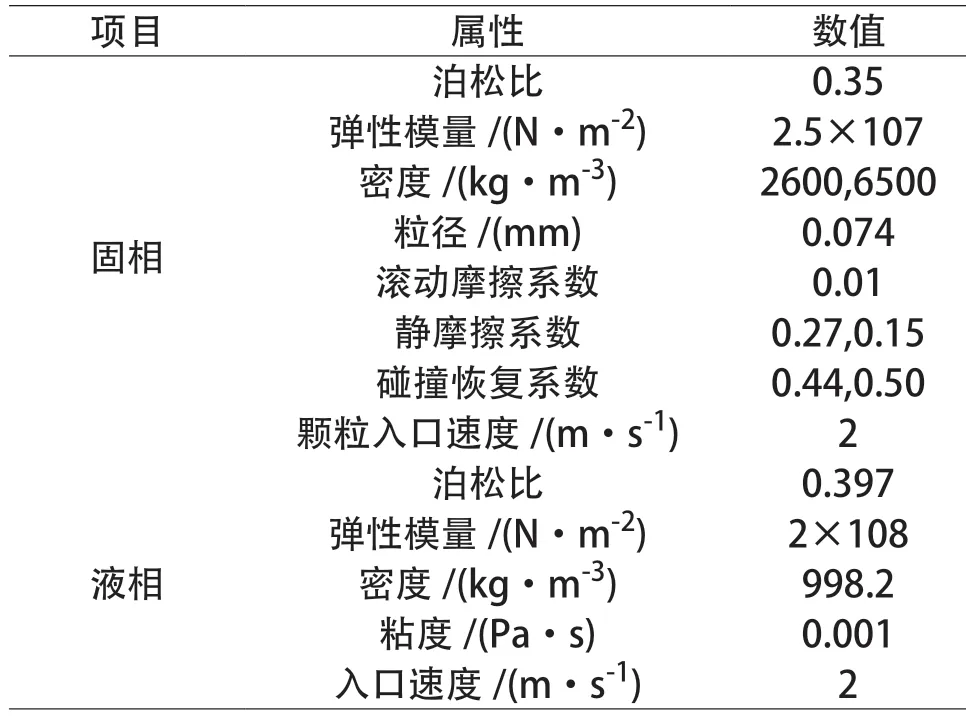
表1 固液两相流仿真参数Table 1 Simulation parameters of solid-liquid two-phase flow

采用DEM-CFD 耦合的方法进行仿真实验，将动量交换源项的数学模型编译进UDF 耦合文件，通过耦合插件UDF 连接EDEM 与Fluent 求解器。

2.2 DEM-CFD 模型验证

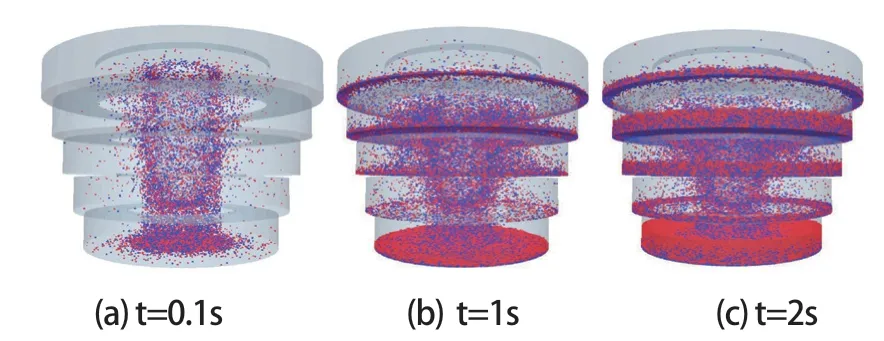
图5 分选锥内矿物颗粒分布Fig. 5 Mineral particle distribution in the separation cone

图5 为不同时刻下分选锥内颗粒群轨迹，其中蓝色、红色分别表征轻、重颗粒。当矿浆从入料口进入选矿机后，将在反冲水冲击力及离心力的作用下进入分选槽中(图6a)；矿物颗粒将从下向上移动至不同的分选槽中，并按轻、重颗粒实现比重分离(图6b)；最终，大部分重颗粒及少量轻颗粒留在富集槽底部，富集槽中分层现象显著(图6c)。根据实际离心选矿机的分选原理，初步验证了本文建立的DEM-CFD 耦合模型的准确性。

2.3 正交仿真优化

为了评定离心选矿机的分选性能，引入回收率和品位作为实验性能评价指标[12]，其中回收率用来评价有用矿物的回收程度，其计算表达式如下：

式中，E1为实际回收率，%；α 为原矿中所含该目标金属质量，kg； β 为精矿中目标金属质量，kg。分选完成后通过EDEM 后处理器计算求得颗粒的回收率。

品位是指矿石中有用组分的含量，其计算表达式如下：

式中，E2为品位，%；γ 为精矿总质量，kg。分选完成后通过EDEM 后处理器分别计算求得相应回收率和品位。

本研究在前期以及前文研究的基础上[13]，以三因素二次回归旋转组合设计安排仿真正交实验，选择反冲水水压、转动频率、给矿流量为实验因素。对实验因素进行单因素预实验，确定其因素水平编码见表2，每个编码重复9 次仿真实验，取其平均值作为仿真结果，仿真实验方案与结果见表3。

表2 因素水平编码Table 2 Factor level coding

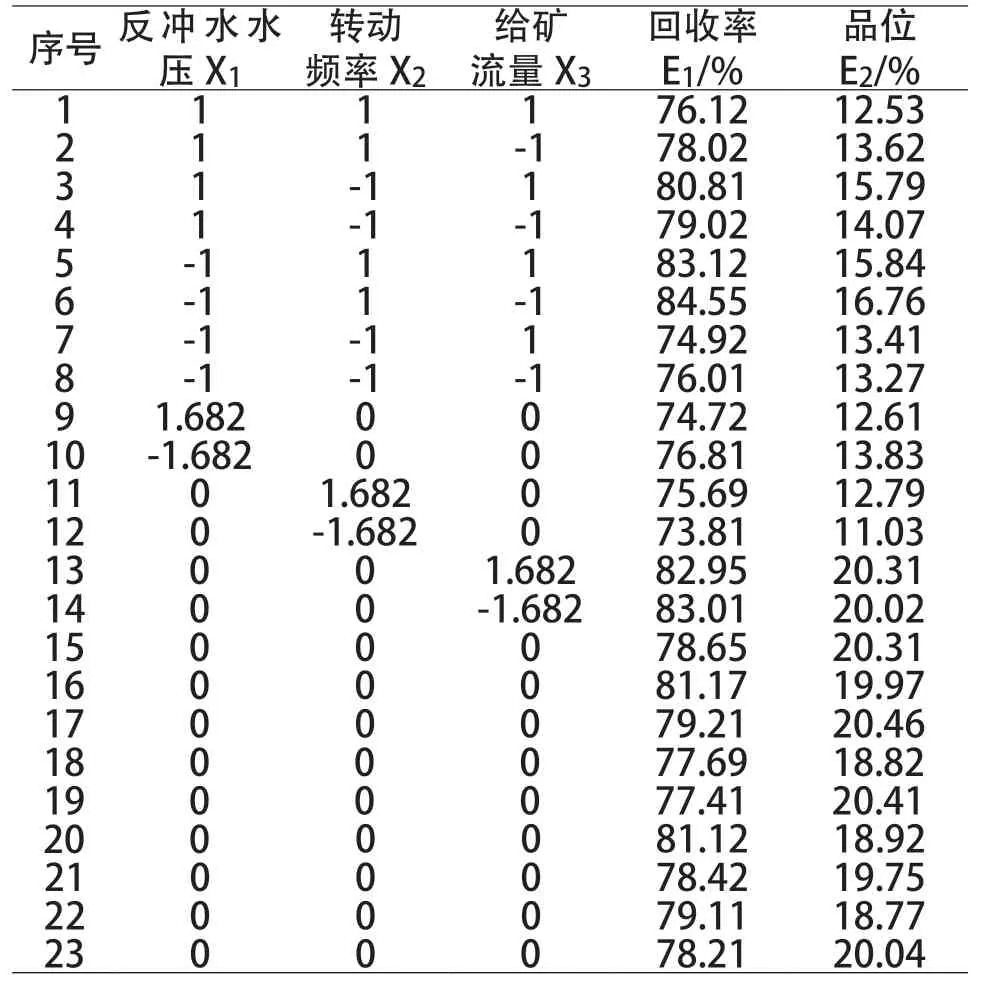
表3 实验方案与结果Table 3 Test scheme and results

2.4 实验结果及分析

实验结果通过SPSS24 对回收率和品位的DEM-CFD 耦合结果展开非线性回归分析，获得回收率与品位的二次回归方程模拟以及回归方程检验见表4。

表4 (a) 回收率回归方程检验Table 4 (a) Test table of regression equation of recovery

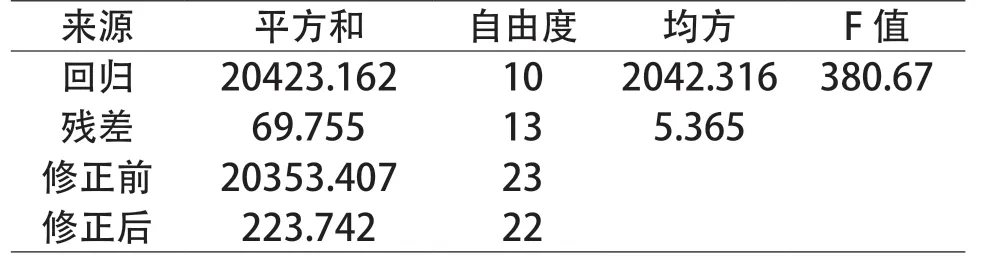
表4 (b) 品位回归方程检验Table 4 (b) Test table of grade regression equation

查F 表得F0.01(10,13)=4.10，因此回归方程高度显著，其二次回归方程模型为：

考虑到文章篇幅，这里重点分析回收率随离心选矿机工艺参数的变化，研究因素的响应面图由MATLAB 2016 a 编程得到见图7。

图7 回收率响应曲面Fig. 7 Response surface diagram of recovery rate

分析图7 可以得到，当给矿流量位于零水平，随着转动频率逐渐增大，回收率与其有着非线性关系，出现了先上升后下降的现象；当转动频率位于零水平时，随着给矿流量的增大，回收率呈现出缓慢上升的趋势。当转动频率位于零水平时，随着反冲水水压的增大，回收率呈现出先上升后下降的趋势；当反冲水水压位于零水平时，随着转动频率的增大，回收率呈现出先上升后下降的趋势。当反冲水水压位于零水平时，随着给矿流量的增大，回收率呈现出先缓慢上升后逐渐下降的趋势，说明给矿流量的变化对回收率影响不大；当给矿流量位于零水平时，随着反冲水水压的增大，回收率呈现先上升后下降的趋势。

从回收率的二次回归方程模型与图7 回收率的响应曲面可以看出，在正交实验因素范围内，三个因素对回收率的显著影响顺序为：反冲水水压对回收率的影响最大，转动频率次之，给矿流量对回收率的影响最小。从品位的回归方程可知，在实验范围内三因素对品位显著性影响大小顺序依次是：反冲水水压、给矿流量和转动频率。该结果表明了离心选矿机工艺参数与回收率和品位之间的关系，为研究离心选矿机的回收率提供了一种新的方法与思路。

2.5 离心选矿机分选工艺参数优化

为寻找实验三因素的较佳工作参数组合，提高立式离心选矿机的分选性能，以回收率和品位最大为约束条件，建立约束方程如下：

根据建立的参数化数学模型，结合实验三因素的取值范围，利用Matlab中非线性优化fmincon函数对约束方程进行求解，参数优化结果为：反冲水水压0.03 MPa，转动频率60.49 Hz，给料速度为0.737 m3/h，此时回收率预测值为82.09%，品位回收率预测值为21.37%。

2.6 离心分选工艺参数的验证

为验证立式离心选矿机仿真分析分选效果能否真实模拟矿石分选实况，对实验室现有的尼尔森选矿机进行离心分选实验。根据分选工艺参数优化结果组合建立仿真与实验结果的对比分析，每项实验进行5 次，取其平均值作为最终结果见表5。

表5 离心分选工艺参数匹配方案Table 5 Matching scheme of centrifugal separation process parameters

从表5 可以看出，对比回收率和品位的预测结果，仿真回收率和品位与实验回收率和品位都有一定程度的降低，且实验回收率和品位均小于仿真值，这主要是因为实验过程中受到测量精度误差、杂质等因素的影响。回收率和品位的预测值、仿真值和实验值误差大小均在5%以内，再次验证了本文所建立基于DEM-CFD 耦合分选模型的有效性和可行性。

分选实验结束后为了观察选矿机的轻重矿料在分选锥中的分布情况，提取分选锥中富集槽的矿料。可以看出分选后的矿料有明显的分层现象，属于轻颗粒的石英砂更多的分布在外层，而比重更大的钨矿主要集中在里层，这与前文DEM-CFD数值模拟得到的分层结果一致。

4 结 论

（1）建立了动量交换源项为流固耦合中的传递介质，并根据分选原理验证了DEM-CFD 模型的正确性，为进行更加符合实际离心选矿机分选过程的数值仿真实验奠定基础。利用EDEM 和FLUENT 对离心选矿机分选过程进行二次正交旋转组合耦合实验，建立了回收率的二次回归方程并得到相应响应曲面，确定了实验因素对回收率的主次因素为：反冲水水压、转动频率和给矿流量。

（2）利用MATLAB 中非线性优化函数fmincon 对约束模型进行寻优处理，在反冲水水压0.03 MPa，转动频率61.5 Hz，给料速度为0.74 m3/h时，分选性能较佳，对仿真优化实验结果进行实际离心分选实验验证，结果表明回收率与品位的预测值、仿真值和实验值误差大小均在5%以内。因此，运用DEM-CFD 对离心选矿机的回收率及品位进行分析具有可行性，同时为离心选矿机工艺参数的匹配优化提供依据。