一种翻滚火箭箭体的运动参数估计方法
2021-05-24赵高鹏范佳杰梁维奎
赵高鹏,范佳杰,梁维奎
(1. 南京理工大学自动化学院,南京 210094;2. 上海宇航系统工程研究所,上海 201108)
0 引 言
空间碎片主动清除的主要目标是安全地捕获和处置太空垃圾,使低地球轨道区域碎片进入大气层烧毁,或使地球静止轨道区域碎片轨道抬高进入坟墓轨道,从而保护在轨航天器运行安全[1]。空间碎片大多属于非合作目标,典型的包括完成任务的火箭箭体、失效卫星等。失效卫星和火箭箭体在空间摄动力作用下一般处于自由翻滚状态,由于其尺寸大、包含未使用的燃料,存在碰撞及爆炸的潜在风险,是在轨主动清除任务中高优先级的目标,获取其在翻滚运动状态下的运动参数是近距离安全逼近和操控的重要前提[2]。
在空间非合作目标的运动参数估计的研究中,常用的测量传感器有单目视觉、双目视觉、ToF深度相机、扫描式激光雷达、非扫描式激光成像雷达等[3-4]。非扫描式激光成像雷达能够实时获取目标的三维量测点云数据,对背景杂散光抑制能力强,且不存在运动模糊,其在空间任务中的应用引起了研究人员的广泛关注[5-6]。
近年来,面向非合作卫星的运动参数估计,国内外学者开展了大量研究[2-3,7-10],文献[7]提出了一种以双目相机对目标特征点的投影作为测量值的解耦估计方法,实现了旋转非合作目标相对状态的估计;文献[8]利用双目相机观测的目标表面特征点的运动规律与目标姿态运动的相关性,实现了对非合作目标角速度与自旋轴的估计;文献[9]基于单目视觉识别并测量目标星固有特征的像素位置为观测输入,通过扩展卡尔曼滤波实现了目标星相对位姿、角速度、惯量比等状态的估计;文献[10] 基于单目视觉,通过提取卫星目标在成像平面的投影角,实现了快旋空间非合作目标自旋速率测量。区别于非合作卫星,非合作火箭箭体呈回转体结构[11],表面光滑,难以稳定地提取图像特征点和计算特征描述,易造成特征误匹配,导致运动参数估计困难。因此,已有面向卫星目标的运动参数估计方法难以直接应用于火箭箭体。
本文以激光成像雷达为测量传感器,直接处理获取的火箭箭体三维稠密点云数据,计算处于自由翻滚状态下的火箭箭体的翻滚轴、章动角和空间章动角速率。
1 坐标系定义
本文中所涉及的坐标系进行定义,如图1所示。目标惯性坐标系{O}:坐标系原点OO位于目标航天器的质心,坐标轴沿目标的惯量主轴方向。坐标轴OOzO为目标的翻滚轴m。

图1 坐标系说明Fig.1 Coordinate system
目标本体坐标系{B}:坐标系原点OB位于目标航天器的质心,坐标轴OBzB位于火箭箭体目标的对称轴上,OBzB与OBxB、OByB组成右手坐标系。火箭箭体的自旋轴l沿坐标轴zB的方向。
服务航天器本体坐标系{H}:坐标系原点OH位于服务航天器的质心。
激光成像雷达测量坐标系{C}:坐标系原点OC位于服务航天器上,OCxC轴沿激光成像雷达视线轴方向,OCxC与OCyC、OCzC组成右手坐标系。目标火箭箭体的运动参数翻滚轴m、章动角度θ、空间章动角速率Ω均在此坐标系中表示。
2 火箭箭体运动状态分析
火箭箭体失去姿态调整能力时,受空间摄动力矩的作用,火箭箭体会表现出复杂的翻滚运动[12-13]。在分离的初始阶段,火箭箭体处于绕最小惯量轴的自旋运动;当火箭箭体受到空间摄动力矩作用,一部分能量随之消耗时,火箭箭体处于存在章动角的翻滚运动;一段时间过后随着总动能趋向最小动能状态,此时火箭箭体处于绕最大惯量轴的平旋运动。
火箭箭体呈回转体结构,可将其看作为圆柱体结构。火箭箭体处于存在章动角的翻滚运动,如图2所示[13]。图中坐标系OBxByBzB为火箭箭体的本体坐标系,坐标系OOxOyOzO为惯性坐标系,l为火箭箭体的自旋轴,其与圆柱体的圆柱轴重合,OBH为翻滚轴及翻滚角动量矩,其中θ为章动角,自旋轴l绕翻滚角动量矩作圆锥运动,其角速率Ω为空间章动角速率。
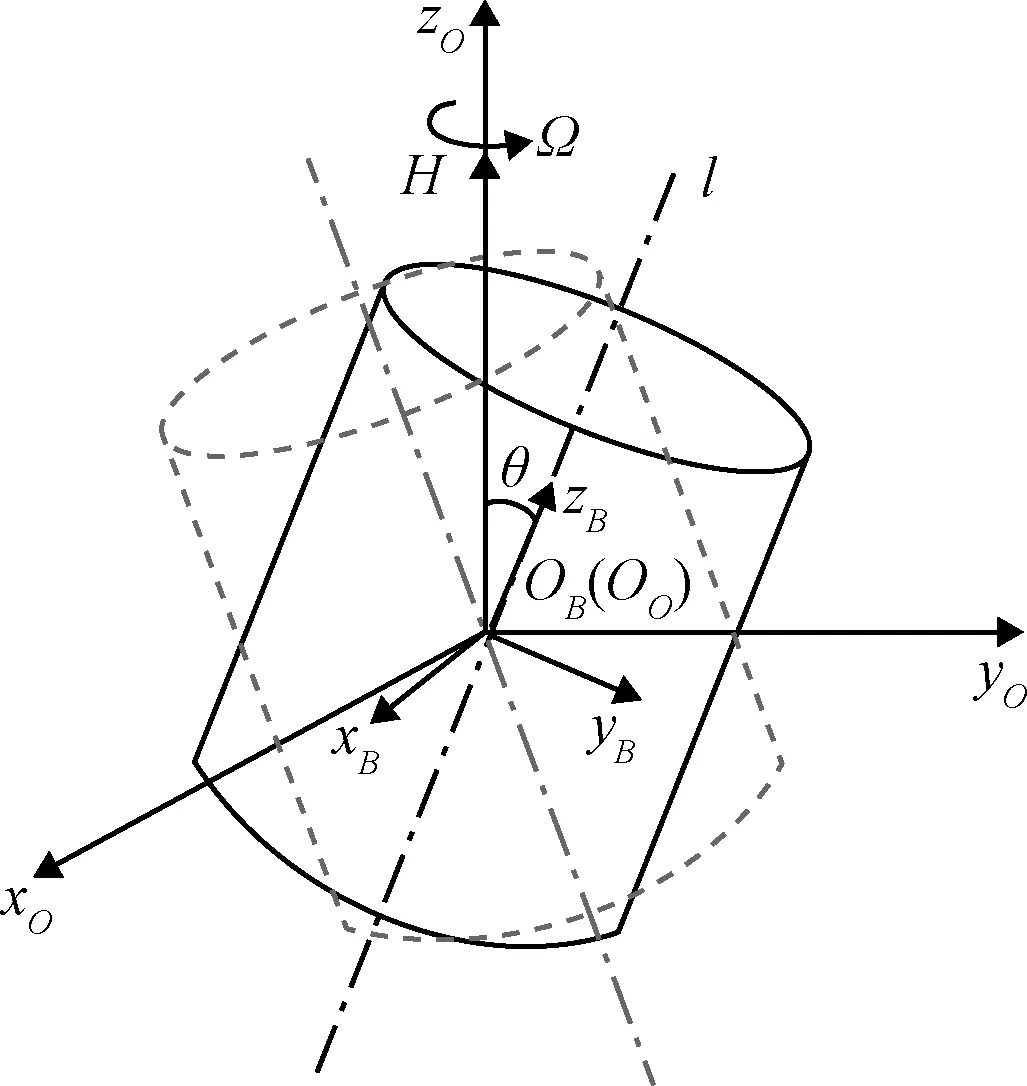
图2 目标带章动角的翻滚运动说明Fig.2 Tumbling motion with nutation angle of target
3 火箭箭体运动参数估计方法
3.1 方法结构
以空间中处于带章动的翻滚运动状态的火箭箭体为研究对象,提出了一种翻滚火箭箭体运动参数估计方法,通过对激光成像雷达获取火箭箭体的三维点云数据进行算法处理,求解得到翻滚轴、章动角和空间章动角速率,其总体框图如图3所示。
本文方法包含三部分,分别为火箭箭体的自旋轴估计、翻滚轴估计、章动角和空间章动角速率的解算。其中,火箭箭体的自旋轴估计的输入为当前时刻激光成像雷达获取的火箭箭体点云数据,通过点云表面法向量估计和随机采样一致性算法,求解得到当前时刻的火箭箭体自旋轴;结合序列帧各时刻得到的火箭箭体自旋轴估计结果,采用递推最小二乘法求解得到翻滚轴;进而结合相邻两帧求得的自旋轴和翻滚轴参数计算出章动角和空间章动角速率。

图3 方法框图Fig.3 The framework of the proposed method
3.2 自旋轴估计
火箭箭体为一个回转体对称结构,可将其视为一个圆柱体,其自旋轴可用圆柱体的轴线表示。因此,火箭箭体的自旋轴估计可通过计算圆柱体的轴线得到。本文采用点云表面法向量估计和随机采样一致性算法对获取的火箭箭体的点云量测数据进行分割,得到呈圆柱体结构的部分点云,同时求解圆柱体点云的自旋轴参数,具体为:
1)点云表面法向量估计
点云表面法向量估计是通过各点及其邻域内的点计算出表面法向量,本文采用基于主成分分析的点云法向量估计,实现过程是通过为每个采样点构建局部邻域,拟合局部邻域最小二乘平面,将拟合平面的法向量作为该采样点的法向量,将曲面变分作为该点处的近似曲率。设Qi为点云数据中的一个采样点,点Qi的3×3协方差矩阵M为
(1)
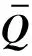
对协方差矩阵M进行特征值分解,协方差矩阵M的最小特征值对应的特征向量即为Qi点的法向量。
设激光成像雷达获得的火箭箭体点云数据的点集为Q{Q1,Q2,…,QN},逐点计算表面法向量,得到每个点对应的法向量集合n{n1,n2,…,nN}。
2)基于随机一致性采样算法的自旋轴估计
空间圆柱体模型的参数由轴线l(ldir,lcen)和半径r表示,其中ldir为轴线的单位方向向量,lcen为轴线上一点,可通过点云集合中的任意两点及其法向量确定,示意图如图4所示。求解过程可描述为:从点云集合中任意选取两点Q1和Q2,分别计算得到其法向量n1和n2,将n1和n2进行叉乘并将结果单位化,则可以确定Q1和Q2所在圆柱体的轴线的单位方向向量ldir。取经过点Q1并垂直l的平面A,将参数直线Q1+tn1和Q2+tn2沿ldir方向投影到平面A,它们的交点即为轴线上的一点lcen。而lcen和Q1在该平面上的投影点之间的距离为圆柱体的半径r[14]。

图4 圆柱体模型示意图Fig.4 Illustration of a cylinder model
随机采样一致性算法(Random sample consensus, RANSAC)是从一组观测数据中,通过迭代的方式匹配已给出的数学模型,找出符合模型的内点并估计出模型的参数。
本文基于RANSAC算法的圆柱体自旋轴估计步骤如下:
步骤1:从点云Q{Q1,Q2,…,QN}中随机选取其中的2个点,{Qi,Qj|i,j∈[1,N]且i≠j}及其法向量ni和nj;
步骤 2:通过点Qi和Qj以及其对应的法向量ni和nj可求解出点Qi和Qj所在的圆柱体模型参数,得到圆柱体的圆柱轴l以及其半径r;
步骤 3:对输入点云数据集中的每一个点{Qd|d∈[1,N]},计算点Qd到估计的圆柱体模型的圆柱轴l的距离rd。设置一个符合条件的点的阈值δ,当满足rd∈[r-δ,r+δ]时,点Qd被记作为内点,否则点Qd被记作为外点;
步骤4:统计所有内点的个数,判断其是否大于设置的最小数目值,如果是,则记录求得的圆柱体模型参数,并存储所有内点作为分割结果,如果不是,则跳到步骤1进行下一轮计算;
步骤5:重复步骤1到步骤4共W次,从中选取内点个数最多的一次,该次求得的圆柱体模型参数即为最符合圆柱体模型的参数,存储的内点为最终得到的分割数据。
通过RANSAC算法求解得到圆柱体的模型参数,其中圆柱轴l即为火箭箭体的自旋轴。
3.3 翻滚轴估计
火箭箭体处于带章动的翻滚运动时,可看作火箭箭体的自旋轴绕翻滚轴旋转,且自旋轴和翻滚轴之间存在一个倾角,该倾斜角即为章动角,如图5所示。
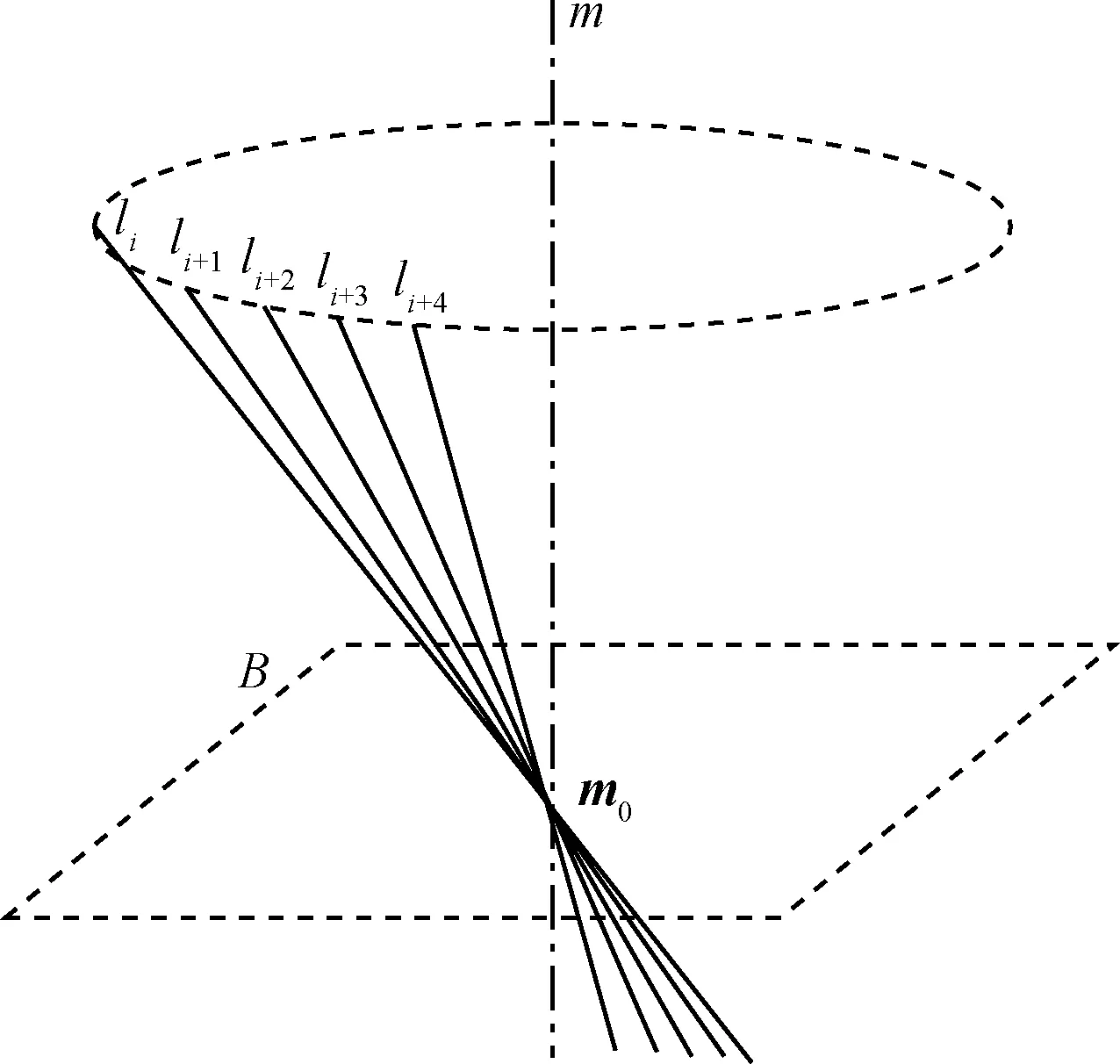
图5 自旋轴轨迹示意图Fig.5 Illustration of spin axis trajectory
图5中,空间直线m表示翻滚轴,li表示第i时刻火箭箭体的自旋轴,平面B为过点m0且垂直于翻滚轴m的平面。在较短的时间里,章动角度可看作为一个定值,不产生变化。除m0点外,火箭箭体的自旋轴任一点的运动轨迹为圆弧轨迹。
翻滚轴m在空间中的参数方程为:
(2)
式中:h为直线方程的参数,点m0(x0,y0,z0)为翻滚轴m上一点,mdir(mx,my,mz)为翻滚轴m的单位方向向量。
因此,翻滚轴的求解可分为两个步骤,即计算翻滚轴上一点m0(x0,y0,z0)以及翻滚轴的单位方向向量mdir(mx,my,mz)。
1)公共点求解
相邻帧之间的自旋轴相交于一个公共点,同时该公共点位于翻滚轴上。图6为相邻自旋轴的示意图,li和li+1分别表示第i时刻和第i+1时刻的火箭箭体的自旋轴,线段pq与li,li+1垂直,点p和点q为相邻两帧自旋轴之间的最近点。

图6 相邻自旋轴示意图Fig.6 Illustration of spin axis of consecutive frame
此时最近点可近似看作为公共点,具体的求解方法为:
已知li和li+1的参数方程:
(3)
式中:Ki和Ki+1分别为自旋轴li和li+1上一点,ldir,i和ldir,i+1分别为自旋轴li和li+1的单位方向向量。
因此,点p和点q可表示为:
(4)
式中:hp和hq为点p和点q的参数。
由于线段pq与li,li+1垂直,其点乘为0,如式(5)所示,将式(4)代入式(5)中,得到式(6)。
(5)
(6)
式中:a,b,c,d,e的表达式见式(7)。
(7)
将式(6)代入到式(4)中,可求得点p和点q的坐标轴值,选取点p作为翻滚轴上的公共点。
2)翻滚轴方向向量求解
由图5可知,自旋轴li和翻滚轴m相交于点m0,由向量的夹角公式可得:
mxli,x+myli,y+mzli,z=cosθ
(8)
式中:ldir,i(li,x,li,y,li,z)和mdir(mx,my,mz)分别表示自旋轴li和翻滚轴m的单位方向向量,θ为章动角。
将式(8)两边同时除以cosθ,0≤θ<π/2得到:
(9)
令
(10)
将式(10)代入式(9)中,可得:
ξxli,x+ξyli,y+ξzli,z=1
(11)
自旋轴li的单位方向向量ldir,i(li,x,li,y,li,z)可由第3.2节得到,此时对翻滚轴m的单位方向向量mdir(mx,my,mz)和章动角θ的求解,可看作是对式(11)的参数ξx,ξy,ξz的求解。
选取连续三帧的数据,根据式(11)即可计算出参数ξx,ξy,ξz。考虑随时间推移,观测得到的自旋轴方向向量数据增多,为充分利用观测得到的自旋轴数据,减小观测数据误差带来的影响,采用带有遗忘因子的最小二乘递推算法来估计参数ξx,ξy,ξz,具体为:
步骤1:将式(11)用矩阵表示;
(12)
式中:ηi=[ξx,ξy,ξz]T,ψi=[li,x,li,y,li,z]T,yi=1。
步骤2:按照式(13)求解得到协方差矩阵Pi+1,增益矩阵Gi+1,其中ρ为遗忘因子,取经验值0.9,I为3×3单位阵;
(13)
步骤3:根据Gi+1的值,按照式(14),求解出i+1时刻的参数ηi+1;
(14)
步骤4:重复步骤2和步骤3,求得每一时刻的参数η。
得到当前时刻的参数η后,将参数单位化,此时得到的向量就是翻滚轴m的单位方向向量。由于至少需要三个时刻的自旋轴测量值,才能计算得到参数η,因此,在序列前两帧不计算,从第三帧开始计算求解,逐帧得到参数计算结果。
3.4 章动角和空间章动角速率求解
1)章动角求解
由式(10)可知ηcosθ=mdir,且0≤θ<π/2,章动角的求解,如式(15)所示:
(15)
式中:|mdir|为mdir的模,|η|为η的模。
2)空间章动角速率求解
求得火箭箭体的翻滚轴和自旋轴后,可从前后两帧中估算出自旋轴绕翻滚轴旋转的空间章动角速率,如图7所示。

图7 自旋轴投影示意图Fig.7 Illustration of spin axis projection
图7中平面B为一垂直于翻滚轴m的平面,将自旋轴li和li+1分别投影到平面B上,得到两条投影线l′i和l′i+1,投影线l′i和l′i+1的夹角υ(0≤υ<π/2)除以相邻帧间的时间间隔即可得到绕翻滚轴旋转的空间章动角速率Ω,求解如式(16)所示:
(16)
式中:mdir表示翻滚轴m的单位方向向量,ldir,i和ldir,i+1分别表示自旋轴li和li+1的单位方向向量,l′dir,i和l′dir,i+1分别表示投影线l′i和l′i+1的单位方向向量,υ表示相邻帧间的空间章动角度,Δt表示相邻帧间的时间间隔。
4 仿真校验
为校验本文中提出算法的有效性与精度,本文采用数字仿真实验,模拟服务航天器在空间环境中对翻滚火箭箭体进行观测,计算翻滚火箭箭体的运动参数,包括翻滚轴、章动角和空间章动角速率。
仿真使用的火箭箭体模型采用NASA官网的土星V型运载火箭的第二级模型,通过有限元分析软件将其转为目标模型点云,如图8所示。

图8 土星V型火箭第二级点云Fig.8 Point clouds of Saturn V rocket stage 2
假设火箭箭体在空间中处于带章动的翻滚运动状态,由欧拉动力学方程可知,为获得带章动的翻滚运动,本体坐标系上各个轴旋转的旋转角速率应满足:
(17)
式中:wx0为绕自旋轴的自旋角速率,wy0和wz0为构成章动角θ的系数,Ωr为本体章动角速率。
对式(17)中的wx,wy和wz做积分:
(18)
式中:φ,φ,λ分别为各个时刻对应的滚转角、俯仰角、偏航角,φ0,φ0,λ0分别为滚转角、俯仰角、偏航角的初始值,初始值均设为0°。
依据式(18)的值,按文献[15]方法,将目标模型点云数据变换到激光成像雷达观测坐标系下,仿真生成激光成像雷达的点云量测数据。
本文实验中设激光成像雷达的参数为:分辨率300×300,视场角20°×20°,传感器测量误差为50 mm。
4.1 测量精度验证
为便于图示,实验设翻滚轴m的直线参数为(ma,mb,mc,md,me,mf),其中(ma,mb,mc)为翻滚轴m的一个公共点,(md,me,mf)为翻滚轴m的单位方向向量。
实验仿真设置:目标惯性坐标系的坐标原点OO在激光成像雷达测量坐标系OCxCyCzC下的坐标为(40,0,0);翻滚轴m的直线参数为(40,0,0,0,1,0);章动角为6.96°,空间章动角速率为10°/s,成像时刻按照0,1,2,…,99,100选取,间隔为1 s,共生成101帧点云量测数据。
本文方法求解翻滚轴方向向量参数,由于其至少需要三个时刻的自旋轴测量值才能计算,因此,本文方法从序列第三帧开始,逐帧计算得到翻滚轴参数、章动角、空间章动角速率。从图9~图14可以看出,前两帧为空,没有计算结果数据。误差计算为本文方法计算的结果减去实验设置的真实值;需特殊说明的是翻滚轴方向向量误差采用本文方法计算的翻滚轴方向向量与方向向量真实值之间的夹角。
图9和图10给出了本文方法得到的翻滚轴参数曲线和误差曲线。图9(a)为翻滚轴公共点参数曲线图,将逐帧计算得到的翻滚轴公共点参数减去其真实参数值(40,0,0),得到翻滚轴公共点参数的误差值,如图9(b)。图10(a)为翻滚轴方向向量参数曲线图,逐帧计算得到的翻滚轴方向向量参数与其真实参数向量(0,1,0)之间的夹角,结果如图10(b)。本文求解翻滚轴方向向量参数的方法采用的是带有遗忘因子的最小二乘递推算法,因此,曲线的变化有一收敛的过程。从图10的曲线变化可知本文方法在第15帧时收敛,得到的翻滚轴公共点参数误差优于1 m,翻滚轴向量参数误差小于0.6°。
图11给出了本文方法得到的章动角曲线及其误差曲线。图11(a)为求解得到的章动角曲线图,

图9 翻滚轴公共点参数曲线和误差曲线Fig.9 Point curves and error curves of tumbling axis

图10 翻滚轴方向向量参数曲线和误差曲线Fig.10 Direction vector curves and error curve of tumbling axis

图11 章动角曲线和误差曲线Fig.11 The nutation angle curve and error curve
从图11(a)的曲线变化可知,第15帧后,章动角收敛,收敛到7°;图11(b)为章动角误差曲线图,由图11(b)可知,章动角收敛后的测量误差小于0.5°。
图12给出了本文方法得到的空间章动角速率曲线及其误差曲线。图12(a)为空间章动角速率曲线,从图12(a)的曲线变化可知,第15帧后,空间章动角速率收敛,收敛到10(°)/s;图12(b)为空间章动角速率误差曲线图,由图12(b)可知,空间章动角速率收敛后的测量误差小于2(°)/s。

图12 空间章动角速率曲线和误差曲线Fig.12 The spatial nutation angular rate curve and error curve
4.2 测量范围验证
1)章动角测量范围分析
分析了火箭箭体在不同的章动角度下本文方法的测量效果。假设在激光成像雷达相机坐标系OCxCyCzC下,火箭箭体的惯性坐标系的坐标原点OO为(40,0,0),其翻滚轴m的直线参数为(40,0,0,0,1,0),火箭箭体绕翻滚轴m做带章动的翻滚运动。绕翻滚轴旋转的空间章动角速率固定为10(°)/s,章动角从15°变化到45°,间隔为15°,成像时刻按照0,1,2,…,99,100选取,间隔为1 s,每次生成101帧点云量测数据。图13给出了在不同章动角的翻滚运动中本文方法计算得到的章动角曲线。
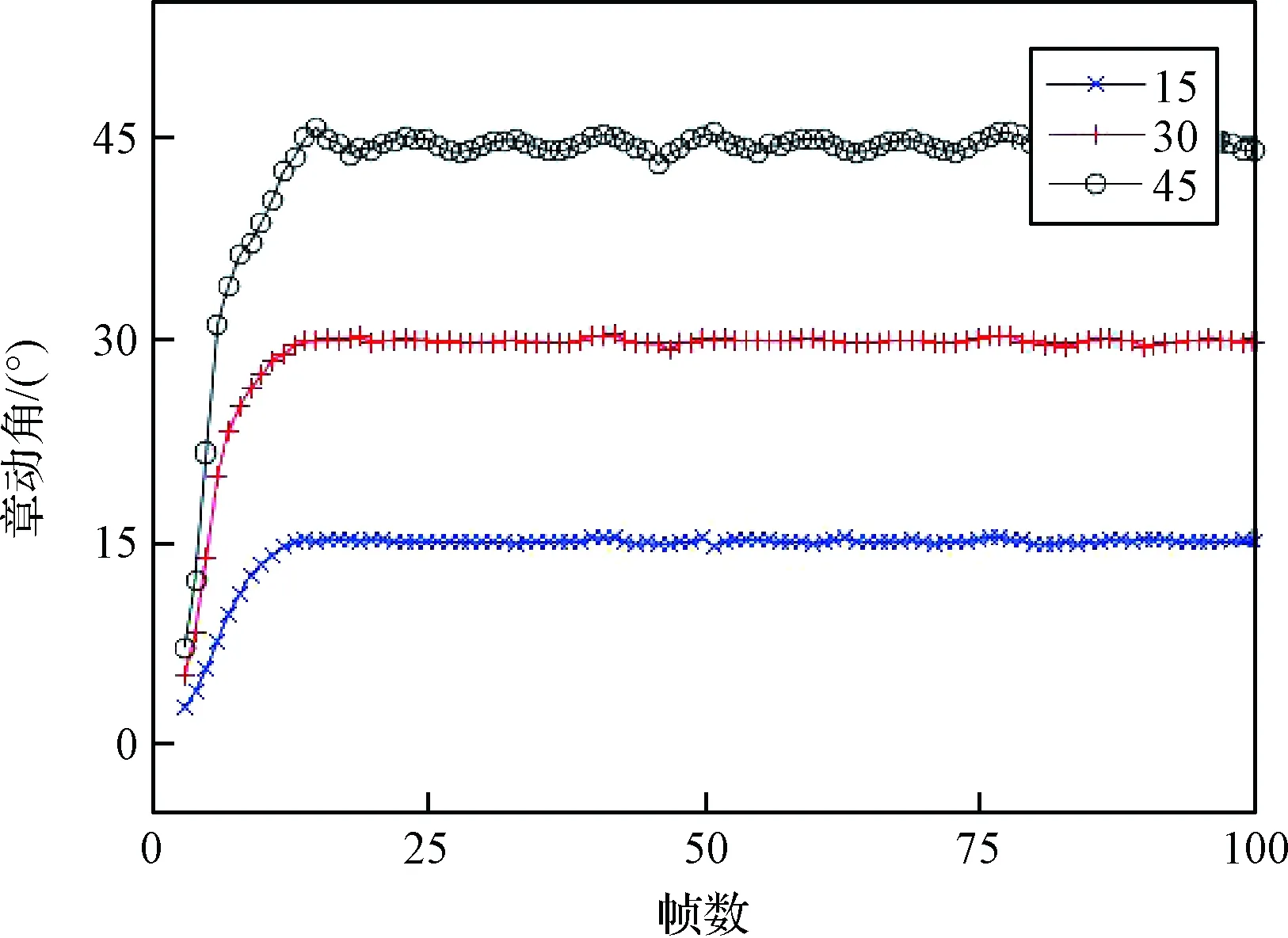
图13 章动角曲线Fig.13 Nutation angle curves
表1给出了当火箭箭体处于15°、30°、45°章动角的翻滚运动时,测量得到的章动角最大误差值。
从图13和表1可知,当火箭箭体处于章动角为15°、30°、45°的翻滚运动时,章动角测量的最大误差随章动角增大而增加,且最大误差在1.3°以内。

表1 章动角测量误差Table1 Nutation angle error
2)空间章动角速率范围测量分析
分析火箭箭体在不同的空间章动角速率下本文方法的测量效果。假设在激光成像雷达测量坐标系OCxCyCzC下,火箭箭体的惯性坐标系的坐标原点OO为(40,0,0),其翻滚轴m的直线参数为(40,0,0,0,1,0),火箭箭体绕翻滚轴m做带章动的翻滚运动。固定章动角为7°,空间章动角速率从10 (°)/s变化到30 (°)/s,间隔为10°,成像时刻按照0,1,2,…,99,100选取,间隔为1 s,每次生成101帧点云量测数据。图14给出了在不同空间章动角速率的翻滚运动中本文方法计算得到的空间章动角速率曲线。
从图14和表2可知,当火箭箭体处于空间章动角速率为10(°)/s、20(°)/s、30(°)/s的翻滚运动时,空间章动角速率测量的误差随空间章动角速率变大而增加。
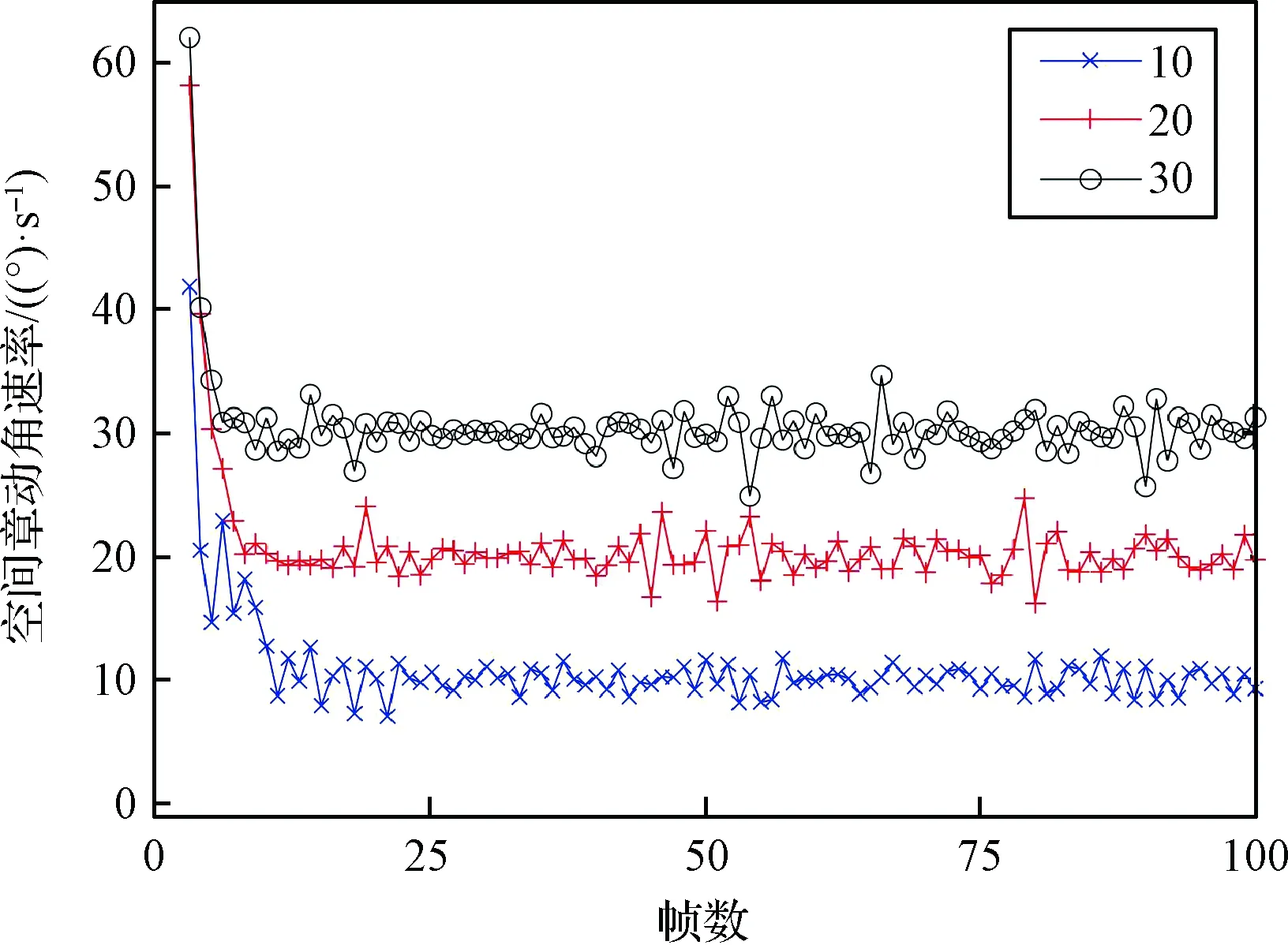
图14 不同空间章动角速率曲线Fig.14 Spatial nutation angular rate curves

表2 空间章动角速率测量误差Table 2 Spatial nutation angle rate error
由实验可知,本文提出的方法能够有效地估计处于翻滚运动状态的火箭箭体的运动参数,得到翻滚火箭箭体的翻滚轴、章动角及空间章动角速率。
5 结 论
针对空间处于自由翻滚运动状态的火箭箭体的运动参数估计问题,提出了一种翻滚火箭箭体的翻滚轴、章动角、空间章动角速率的估计方法。以激光成像雷达获取的点云数据为输入,通过点云表面法向量估计和随机采样一致性算法计算出自旋轴,在此基础上,利用序列帧数据进一步求解得到翻滚轴参数、章动角和空间章动角速率;通过仿真实验验证了方法的有效性,结果表明本文方法适用于翻滚火箭箭体的运动参数测量,具有较好的运动参数估计精度和适用范围,为分析激光成像雷达参数与翻滚目标运动参数估计结果关系的研究奠定基础。
